电子技术——电流镜负载的差分放大器
电子技术——电流镜负载的差分放大器

目前我们学习的差分放大器都是使用的是差分输出的方式,即在两个漏极之间获取电压。差分输出主要有以下优势:
- 降低了共模信号的增益,提高了共模抑制比。
- 降低了输入偏移电压。
- 提升了差分输入的增益。
由于差分输出巨大的优势使得几乎大部分集成IC放大器的初级输入都使用了 差分输入,差分输出 的模式,例如运算放大器。这使得集成IC放大器拥有优越的信号抗干扰能力,特别是针对于共模信号。尽管如此,有时我们不得不使用单端输出的方式,例如片外负载。下图展示了一个运算放大器基本原理图:

这个运算放大器前两级都是使用的差分输入,差分输出,最后一级将差分输出转换为单端输出。我们现在就来解决差分输出转换为单端输出的问题。
差分到单端输出
下图展示了一个最简单的差分到单端输出的方案:

仅仅用一个输出端作为输出,因此 Q1Q_1Q1 的负载电阻是可以省略的。但是这个电路有一个缺点,就是损失了一半的电压增益,而且还浪费了 Q1Q_1Q1 的电流。一个更好的方法是将 Q1Q_1Q1 的电流利用起来,这就是我们要讨论的。
电流镜负载的MOS差分放大器
下图展示了一个MOS差分放大器,只不过负载变成了一个电流镜:

为了说明该电路的工作方式,我们先讨论平衡的情况,也就是令 vG1=vG2=0v_{G1} = v_{G2} = 0vG1=vG2=0 如图:

因为电路的对称的,因此MOS Q1Q_1Q1 和 Q2Q_2Q2 的漏极电流相等且都为 I/2I/2I/2 ,其中 Q1Q_1Q1 的电流流向电流镜的电流采集输入 Q3Q_3Q3 ,这将在 Q4Q_4Q4 复制出电流 I/2I/2I/2 。观察输出节点,我们发现从 Q4Q_4Q4 流入和从 Q2Q_2Q2 流出的电流均为 I/2I/2I/2 ,也就是说输出电流为零,这正是我们想要的结果。而且,假设 Q3Q_3Q3 和 Q4Q_4Q4 完全匹配,此时的输出电压应为 VO=VDD−VSG3V_O = V_{DD} - V_{SG3}VO=VDD−VSG3 。值得注意的是,实际情况下电路总是不对称的,因此存在净电流从输出端流出,在缺少负载电阻的情况下,净电流通过 Q4Q_4Q4 和 Q2Q_2Q2 的输出阻抗,这将造成输出电压与理论值存在较大的偏差。因此这个电路的偏置通常被负反馈所控制,之后我们会学习到。
接下来考虑应用一个差分信号 vidv_{id}vid ,如图:

因为我们讨论的是小信号,所有我们移除了所有的DC分量。根据我们之前的分析, Q1Q_1Q1 和 Q2Q_2Q2 的源极电流仍为:
i=vid/(2gm)i = v_{id} /(\frac{2}{g_m}) i=vid/(gm2)
各个支路的电流方向如图所示,我们发现,流出输出节点的电流变成了 2i2i2i ,我们无损的做到了将差分输出转为了单端输出。我们这里省略了输出负载,实际上的输出电压由 2i2_i2i 和输出负载共同决定。
实际上,这个电路的精髓就在于:当输入的是共模信号的时候, Q4Q_4Q4 输出的电流被 Q2Q_2Q2 抵消。当输入的是差分信号的时候,此时 Q4Q_4Q4 输出的电流被 Q2Q_2Q2 叠加。
电流镜负载的差分放大器的差分增益
我们知道在IC中, ror_oro 的作用无法忽视。因此我们将在考虑 ror_oro 的情况下计算 vo/vidv_o / v_{id}vo/vid 的值。我们发现,若考虑 ror_oro ,那么电路本身是不对称的,因为 Q1Q_1Q1 看向 Q3Q_3Q3 的阻抗较小,大约为 1/gm31/g_{m3}1/gm3 ,而 Q2Q_2Q2 看向 Q4Q_4Q4 的阻抗是较大的,大约为 ro4r_{o4}ro4 ,此时共源极端点不再是虚拟地,因此我们不能使用半电路分析法。
我们的分析方法是,将电路等效为一般形式:

这里 GmvidG_m v_{id}Gmvid 是电流镜负载的差分放大器的输出信号电压, RoR_oRo 是输出阻抗。我们先给出结论:
这里 GmG_mGm 是整体传导系数,其值为:
Gm=gm1,2G_m = g_{m1,2} Gm=gm1,2
这里 gm1,2g_{m1,2}gm1,2 是Q1Q_1Q1 和 Q2Q_2Q2 的互导系数。
Ro=ro2∣∣ro4R_o = r_{o2} || r_{o4} Ro=ro2∣∣ro4
此时开路电压增益为:
Ad≡vovid=GmRo=gm1,2(ro2∣∣ro4)A_d \equiv \frac{v_o}{v_{id}} = G_mR_o = g_{m1,2}(r_{o2} || r_{o4}) Ad≡vidvo=GmRo=gm1,2(ro2∣∣ro4)
我们将 gm1,2g_{m1,2}gm1,2 简记为 gmg_mgm ,并且令 ro2=ro4=ror_{o2} = r_{o4} = r_oro2=ro4=ro ,则:
Ad=12gmro=12A0A_d = \frac{1}{2}g_m r_o = \frac{1}{2}A_0 Ad=21gmro=21A0
这里 A0A_0A0 是固有增益。
首先我们推导短路互导系数,下图中,我们将输出端置地:

则短路互导系数定义为:
Gm≡iovidG_m \equiv \frac{i_o}{v_{id}} Gm≡vidio
观察到将输出端置地后,此时的电路几乎是平衡状态,因为从 Q1Q_1Q1 看向 Q3Q_3Q3 是一个接近零的小阻抗,从 Q2Q_2Q2 看向 Q4Q_4Q4 此时阻抗为零。因此我们近似的将共源极端点的电压看做是零点。紧接着我们将其使用混合 π\piπ 模型展开,注意到 Q3Q_3Q3 可以看做是输出阻抗为 1/gm3∣∣ro31/g_{m3}||r_{o3}1/gm3∣∣ro3 的二极管:

通过节点电压法我们能够写出:
io=gm2(vid2)−gm4vgs4i_o = g_{m2}(\frac{v_{id}}{2})-g_{m4}v_{gs4} io=gm2(2vid)−gm4vgs4
注意到:
vgs3=vgs4v_{gs3} = v_{gs4} vgs3=vgs4
而且:
vgs3=−gm1(vid2)(1gm3∣∣ro3∣∣ro1)v_{gs3} = -g_{m1}(\frac{v_{id}}{2})(\frac{1}{g_{m3}}||r_{o3}||r_{o1}) vgs3=−gm1(2vid)(gm31∣∣ro3∣∣ro1)
因为 1gm3≪ro3,ro1\frac{1}{g_{m3}} \ll r_{o3},r_{o1}gm31≪ro3,ro1 所以:
vgs3≃−gm1gm3(vid2)v_{gs3} \simeq -\frac{g_{m1}}{g_{m3}}(\frac{v_{id}}{2}) vgs3≃−gm3gm1(2vid)
若此时 gm3=gm4g_{m3} = g_{m4}gm3=gm4 并且 gm1=gm2=gmg_{m1} = g_{m2} = g_mgm1=gm2=gm 则:
io=gmvidi_o = g_m v_{id} io=gmvid
则:
Gm=gmG_m = g_m Gm=gm
最后我们推导输出阻抗 RoR_oRo ,下图中我们将输入端置地,在输出端接入测试电压源:

则输出阻抗定义为:
Ro≡vxixR_o \equiv \frac{v_x}{i_x} Ro≡ixvx
在图中,我们将分析顺序使用编号标出,电流 iii 依次流入 Q2Q_2Q2 Q1Q_1Q1 ,因为 Q3Q_3Q3 是二极管接法,而且 1/gm3≪ro31/g_{m3} \ll r_{o3}1/gm3≪ro3 所以大部分电流都流入 Q3Q_3Q3 ,这将导致在 Q4Q_4Q4 也复制出相同的电流 iii 。根据输出端点电压:
i=ix/Ro2i = i_x / R_{o2} i=ix/Ro2
这里 Ro2R_{o2}Ro2 是从输出端点向下看的阻抗。为了计算 Ro2R_{o2}Ro2 我们先计算电流镜 Q3Q_3Q3 的输入阻抗:
Rin3=1gm3∣∣ro3≃1gm3R_{in3} = \frac{1}{g_{m3}}||r_{o3} \simeq \frac{1}{g_{m3}} Rin3=gm31∣∣ro3≃gm31
然后是CG放大器 Q1Q_1Q1 的输入阻抗,在上一章我们计算过为:
Rin1=ro1+RLgm1ro1R_{in1} = \frac{r_{o1} + R_L}{g_{m1}r_{o1}} Rin1=gm1ro1ro1+RL
带入 RL=Rin3=1gm3R_L = R_{in3} = \frac{1}{g_{m3}}RL=Rin3=gm31 :
Rin1=1gm1+1/gm3gm1ro1≃1gm1R_{in1} = \frac{1}{g_{m1}} + \frac{1/g_{m3}}{g_{m1}r_{o1}} \simeq \frac{1}{g_{m1}} Rin1=gm11+gm1ro11/gm3≃gm11
此时 Ro2R_{o2}Ro2 是CG放大器 Q2Q_2Q2 的输出阻抗,在上一章我们计算过为:
Ro2=Rin1+ro2+gm2ro2Rin1=1gm1+ro2+gm2gm1ro2R_{o2} = R_{in1} + r_{o2} + g_{m2}r_{o2}R_{in1} = \frac{1}{g_m1} + r_{o2} + \frac{g_{m2}}{g_{m1}}r_{o2} Ro2=Rin1+ro2+gm2ro2Rin1=gm11+ro2+gm1gm2ro2
这里令 gm1=gm2=gmg_{m1} = g_{m2} = g_mgm1=gm2=gm 则:
Ro2≃2ro2R_{o2} \simeq 2r_{o2} Ro2≃2ro2
带回原方程我们得到:
ix=i+i+vxro4=2vxRo2+vxro4=vxro2+vxro4i_x = i + i + \frac{v_x}{r_{o4}} = 2 \frac{v_x}{R_{o2}} + \frac{v_x}{r_{o4}} = \frac{v_x}{r_{o2}} + \frac{v_x}{r_{o4}} ix=i+i+ro4vx=2Ro2vx+ro4vx=ro2vx+ro4vx
所以:
Ro=ro2∣∣ro4R_o = r_{o2} || r_{o4} Ro=ro2∣∣ro4
电流镜负载的BJT差分放大器
BJT版本的电流镜负载的BJT差分放大器如下图所示:

在这里我们忽略有限 β\betaβ 的基极电流的影响,并且假设电路是平衡的,我们分析的方法和MOS一样。其中短路互导系数为:
Gm=gm1,2G_m = g_{m1,2} Gm=gm1,2
输出阻抗为:
Ro=ro2∣∣ro4R_o = r_{o2} || r_{o4} Ro=ro2∣∣ro4
与MOS一致。
开路差分增益为:
Ad=vovid=GmRo=gm(ro2∣∣ro4)A_d = \frac{v_o}{v_{id}} = G_mR_o = g_m(r_{o2} || r_{o4}) Ad=vidvo=GmRo=gm(ro2∣∣ro4)
这里若 gm1=gm2=gm=VTI/2g_{m1} =g_{m2} =g_m = \frac{V_T}{I/2}gm1=gm2=gm=I/2VT 以及 ro2=ro4=ror_{o2} = r_{o4} = r_oro2=ro4=ro ,则:
Ad=12gmroA_d = \frac{1}{2} g_m r_o Ad=21gmro
以上均和MOS的情况一致,但是BJT的 gmg_mgm 要比MOS的大很多因此增益要比MOS大,但是因为基极电流的影响,其存在有限的输入阻抗:
Rid=2rπR_{id} = 2 r_\pi Rid=2rπ
系统性输入偏移电压误差
考虑到BJT电流镜即使完全匹配,其电流传导比也不是单位一。因此在BJT电流镜中存在系统误差,如图:

此时 Q4Q_4Q4 输出的电流为:
I4=αI/21+2βpI_4 = \frac{\alpha I/2}{1 + \frac{2}{\beta_p}} I4=1+βp2αI/2
与 Q2Q_2Q2 的输出电流不匹配,因此输出端存在净电流:
Δi=αI2−αI/21+2βp≃αIβp\Delta i = \frac{\alpha I}{2} - \frac{\alpha I/2}{1 + \frac{2}{\beta_p}} \simeq \frac{\alpha I}{\beta_p} Δi=2αI−1+βp2αI/2≃βpαI
为了让误差归零,我们必须额外的输入差分电压:
VOS=−ΔiGm=−2VTβpV_{OS} = -\frac{\Delta i}{G_m} = -\frac{2V_T}{\beta_p} VOS=−GmΔi=−βp2VT
一个改进的方法是使用高级电流镜。
共模增益和共模抑制
电路在任何时候都不是理想情况,因此电流镜负载的差分放大器也存在共模增益和共模抑制。因为电流镜的传导比实际上是一个非常接近于单位一的数字,当输入一个共模信号,和 Q2Q_2Q2 的抵消电流就会出现不相等的情况,因此存在一个共模信号输出。我们希望推导出 AcmA_{cm}Acm 。下图是我们使用的电路图:

注意到我们省去了DC偏移,并且只留下了 RSSR_{SS}RSS 。尽管负载电路是不对称的,但是这不影响我们可以将 RSSR_{SS}RSS 拆开为:

这相当于带源极电阻 2RSS2R_{SS}2RSS 的CS放大器。其等效模型为:

为了决定 GmcmG_{mcm}Gmcm 的大小,我们将 Q1Q_1Q1 的漏极置地得到:
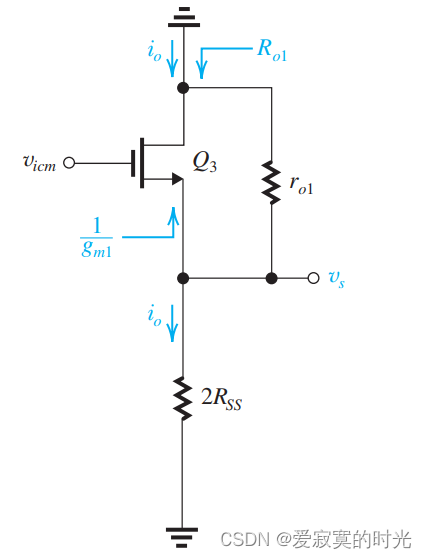
在上图中:
vs=vicm(2RSS∣∣ro1)(2RSS∣∣ro1)+(1/gm1)≃vicmv_s = v_{icm} \frac{(2R_{SS}||r_{o1})}{(2R_{SS}||r_{o1}) + (1/g_{m1})} \simeq v_{icm} vs=vicm(2RSS∣∣ro1)+(1/gm1)(2RSS∣∣ro1)≃vicm
则 ioi_oio 为:
io=vc2RSS≃vicm2RSSi_o = \frac{v_c}{2R_{SS}} \simeq \frac{v_{icm}}{2R_{SS}} io=2RSSvc≃2RSSvicm
所以互导系数为:
Gmcm≡iovicm=12RSSG_{mcm} \equiv \frac{i_o}{v_{icm}} = \frac{1}{2R_{SS}} Gmcm≡vicmio=2RSS1
RoR_oRo 是带源极电阻的CS放大器的输出阻抗为:
Ro1=2RSS+ro1+(gm1ro1)(2RSS)R_{o1} = 2R_{SS} + r_{o1} + (g_{m1}r_{o1})(2R_{SS}) Ro1=2RSS+ro1+(gm1ro1)(2RSS)
同样的:
Ro2=2RSS+ro2+(gm2ro2)(2RSS)R_{o2} = 2R_{SS} + r_{o2} + (g_{m2}r_{o2})(2R_{SS}) Ro2=2RSS+ro2+(gm2ro2)(2RSS)
现在对于电流镜的输入阻抗为 RimR_{im}Rim 电流传导比为 AmA_mAm 输出阻抗为 RomR_{om}Rom 这对于任何的电流源均适用,因为 Ro1R_{o1}Ro1 要远大于 RimR_{im}Rim 所以电流源的输入电流为 iii_iii :
ii≃Gmcmvicmi_i \simeq G_{mcm} v_{icm} ii≃Gmcmvicm
此时输出电压为:
vo=(Amii−Gmcmvicm)(Rom∣∣Ro2)v_{o} = (A_m i_i - G_{mcm}v_{icm})(R_{om} || R_{o2}) vo=(Amii−Gmcmvicm)(Rom∣∣Ro2)
全部带入得到:
Acm≡vovicm=−(1−Am)Gmcm(Rom∣∣Ro2)A_{cm} \equiv \frac{v_o}{v_{icm}} = -(1 - A_m)G_{mcm}(R_{om} || R_{o2}) Acm≡vicmvo=−(1−Am)Gmcm(Rom∣∣Ro2)
这是一个通用的公式,适用于所有的电流镜。针对于简单电流镜:
Rim=1gm3∣∣ro3R_{im} = \frac{1}{g_{m3}} || r_{o3} Rim=gm31∣∣ro3
Rom=ro4R_{om} = r_{o4} Rom=ro4
电流增益为:
Amii=−gm4vgs4=−gm4vgs3A_m i_i = -g_{m4}v_{gs4} = -g_{m4}v_{gs3} Amii=−gm4vgs4=−gm4vgs3
这里:
vgs3=−iiRinv_{gs3} = -i_i R_{in} vgs3=−iiRin
因此:
Am=gm4RinA_{m} = g_{m4}R_{in} Am=gm4Rin
假设 gm4=gm3g_{m4} = g_{m3}gm4=gm3 有:
Am=1/(1+1gm3ro3)A_m = 1 / (1 + \frac{1}{g_{m3} r_{o3}}) Am=1/(1+gm3ro31)
整体带入得到:
Acm≃−12gm3RSSA_{cm} \simeq -\frac{1}{2g_{m3}R_{SS}} Acm≃−2gm3RSS1
这是因为 ro4≪Ro2,ro4=ro3,gmro3≪1r_{o4} \ll R_{o2},r_{o4} = r_{o3},g_{m}r_{o3} \ll 1ro4≪Ro2,ro4=ro3,gmro3≪1 。
因此共模抑制比为:
CMRR=≡∣Ad∣∣Acm∣=[gm(ro2∣∣ro4)][2gm3RSS]CMRR = \equiv \frac{|A_d|}{|A_{cm}|} = [g_m(r_{o2} || r_{o4})][2g_{m3}R_{SS}] CMRR=≡∣Acm∣∣Ad∣=[gm(ro2∣∣ro4)][2gm3RSS]
对于 ro2=ro4=ror_{o2} = r_{o4} = r_oro2=ro4=ro 并且 gm3=gmg_{m3} = g_mgm3=gm 来说:
CMRR=(gmro)(gmRSS)CMRR = (g_mr_o)(g_mR_{SS}) CMRR=(gmro)(gmRSS)
我们发现要提高CMRR可以提高偏置电流 III 或者提供输出阻抗,这可以使用共源共栅电流镜或者高级电流镜。
BJT情况
对于BJT来说:
Gmcm=12REEG_{mcm} = \frac{1}{2R_{EE}} Gmcm=2REE1
并且:
Rim=1gm3∣∣rπ3∣∣rπ4∣∣ro3R_{im} = \frac{1}{g_{m3}} || r_{\pi 3} || r_{\pi 4} || r_{o3} Rim=gm31∣∣rπ3∣∣rπ4∣∣ro3
因为 ro3≫rπ3r_{o3} \gg r_{\pi 3}ro3≫rπ3 并且 rπ3=rπ4r_{\pi 3} = r_{\pi 4}rπ3=rπ4 得到:
Rim≃1gm3∣∣2rπ3R_{im} \simeq \frac{1}{g_{m3}} || \frac{2}{r_{\pi 3}} Rim≃gm31∣∣rπ32
Rom=ro4R_{om} = r_{o4} Rom=ro4
电流传导比为:
Am=gm4RimA_{m} = g_{m4}R_{im} Am=gm4Rim
假设 gm4=gm3g_{m4} = g_{m3}gm4=gm3 使用 ro4≫Ro2r_{o4} \gg R_{o2}ro4≫Ro2 :
Acm≃−ro42REE2rπ3gm3+2rπ3≃−ro42REE2β3=−ro4β3REEA_{cm} \simeq -\frac{r_{o4}}{2R_{EE}}\frac{\frac{2}{r_{\pi 3}}}{g_{m3} + \frac{2}{r_{\pi 3}}} \simeq -\frac{r_{o4}}{2R_{EE}} \frac{2}{\beta_3} = -\frac{r_{o4}}{\beta_3 R_{EE}} Acm≃−2REEro4gm3+rπ32rπ32≃−2REEro4β32=−β3REEro4
则共模抑制比为:
CMRR=gm(ro2∣∣ro4)(β3REEro4)CMRR = g_{m}(r_{o2}||r_{o4})(\frac{\beta_3R_{EE}}{r_{o4}}) CMRR=gm(ro2∣∣ro4)(ro4β3REE)
对于 ro2=ro4=ror_{o2} = r_{o4} = r_oro2=ro4=ro 来说:
CMRR=12β3gmREECMRR = \frac{1}{2}\beta_3 g_m R_{EE} CMRR=21β3gmREE
同样的为了提高BJT的CMRR,我们可以使用较大的偏置电流,或者使用较高输出阻抗的高级电流镜。
总结:电流镜负载的差分放大器共模增益主要原因是由于电流镜的电流传导比上的误差,对于MOS来说这是由于 ro3r_{o3}ro3 引起的,对于BJT来说是由于有限的 β\betaβ 引起的。
相关文章:

电子技术——电流镜负载的差分放大器
电子技术——电流镜负载的差分放大器 目前我们学习的差分放大器都是使用的是差分输出的方式,即在两个漏极之间获取电压。差分输出主要有以下优势: 降低了共模信号的增益,提高了共模抑制比。降低了输入偏移电压。提升了差分输入的增益。 由于…...

go面试题
1.json包在使用的时候,结构体里的变量不加tag能不能正常转成json里的字段? 如果变量首字母小写,则为private。无论如何不能转,因为取不到反射信息。如果变量首字母大写,则为public。 不加tag,可以正常转为j…...

攻防世界-Confusion1
题目 访问题目场景 某天,Bob说:PHP是最好的语言,但是Alice不赞同。所以Alice编写了这个网站证明。在她还没有写完的时候,我发现其存在问题。(请不要使用扫描器) 然后结合图片我们知道,这个网址是python写的࿰…...

机器学习实战--梯度下降法进行波士顿房价预测
前言: Hello大家好,我是Dream。 今天来学习一下如何使用机器学习梯度下降法进行波士顿房价预测,这是简单的一个demo,主要展示的是一些小小的思路~ 本文目录:一、波士顿房价预测1.全部的数据可视化2.地理数据可视化3.房…...

黑马】后台管理-项目优化和上线
一。项目优化优化1,加载进度条显示安装一个运行依赖,nprogress然后导包,调用对象展示和隐藏在main中基于拦截器实现展示进度条和隐藏进度条的效果如果触发请求拦截器,证明发起请求,希望展示进度条,如果触发…...
数据库-MySQL)
Web 框架 Flask 快速入门(三)数据库-MySQL
课程地址:Python Web 框架 Flask 快速入门 文章目录数据库1、数据库的安装与配置2、数据库的简单使用——增删改1. 定义数据模型2. 增删改3、 关系引用——表的关联4、查询——通过SQLAlchemy扩展5、其他1. 数据模型的实现(疑惑)6、Bug记录1.…...
牛客网Python篇数据分析习题(六)
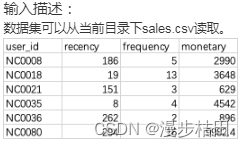
1.某公司计划举办一场运动会,现有运动会项目数据集items.csv。 包含以下字段: item_id:项目编号; item_name:项目名称; location:比赛场地。 有员工报名情况数据集signup.csv。包含以下字段: employee_id&a…...

Ansible的安装及部署
目录 一、Ansible对于企业运维的重大意义 二、Ansible的安装 三、构建Ansible清单 1.直接书写受管主机名或ip,每行一个 2.设定受管主机的组[组名称] 四、Ansible配置文件参数详解 1、配置文件的分类与优先级 2.配置新用户的Ansible配置 3.生成免密认证 本章…...
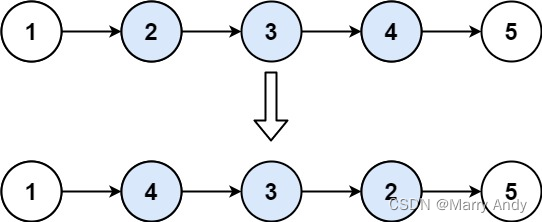
链表题目总结 -- 递归
目录一. 递归反转整个链表1. 思路简述2. 代码3. 总结二. 反转链表前 N 个节点1. 思路简述2. 代码3. 总结三、反转链表的一部分1. 思路简述2. 代码3.总结四、从节点M开始反转后面的链表1. 思路简述2. 代码3.总结一. 递归反转整个链表 题目链接:https://leetcode.cn/…...
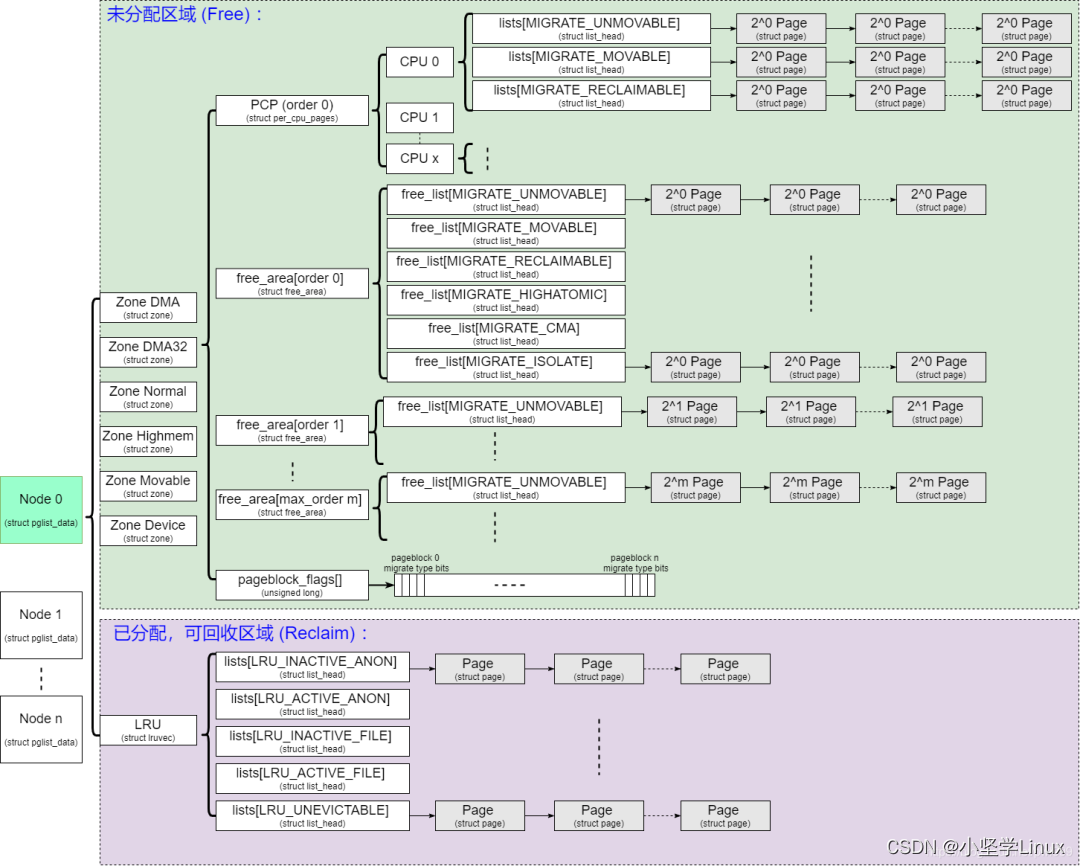
重写-linux内存管理-伙伴分配器(一)
文章目录一、伙伴系统的结构二、初始化三、分配内存3.1 prepare_alloc_pages3.2 get_page_from_freelist3.2.1 zone_watermark_fast3.2.2 zone_watermark_ok3.2.3 rmqueue3.2.3.1 rmqueue_pcplist3.2.3.2 __rmqueue3.2.3.2.1 __rmqueue_smallest3.2.3.2.2 __rmqueue_fallback3.…...
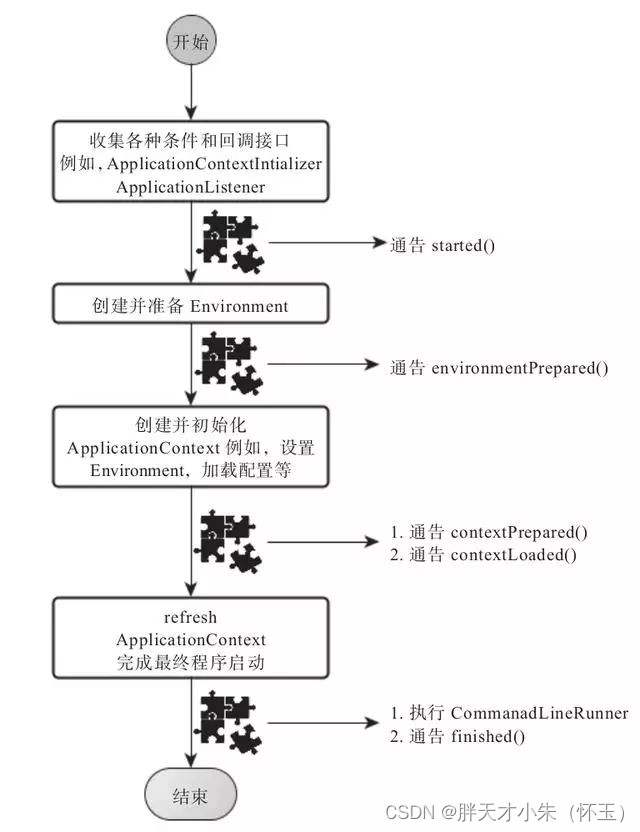
为什么要用springboot进行开发呢?
文章目录前言1、那么Springboot是怎么实现自动配置的1.1 启动类1.2 SpringBootApplication1.3 Configuration1.4 ComponentScan1.5 EnableAutoConfiguration1.6 两个重要注解1.7 AutoConfigurationPackage注解1.8 Import(AutoConfigurationImportSelector.class)注解1.9自动配置…...

设备树信息解析相关函数
一。可以通过三种不同的方式解析设备树节点: 1.根据设备树节点的名字解析设备树节点 struct device_node *of_find_node_by_name(struct device_node *from, const char *name); 参数: from:当前节点父节点首地址 name:设备树节点名字 …...

LeetCode-1124. 表现良好的最长时间段【哈希表,前缀和,单调栈】
LeetCode-1124. 表现良好的最长时间段【哈希表,前缀和,单调栈】题目描述:解题思路一:查字典。cur是当前的前缀和(劳累与不劳累天数之差),向前遍历。有两种情况。情况一,若cur大于0则是[0,i]的劳累与不劳累天…...
vue-router路由配置
介绍:路由配置主要是用来确定网站访问路径对应哪个文件代码显示的,这里主要描述路由的配置、子路由、动态路由(运行中添加删除路由) 1、npm添加 npm install vue-router // 执行完后会自动在package.json中添加 "vue-router…...

中国计算机设计大赛来啦!用飞桨驱动智慧救援机器狗
中国大学生计算机设计大赛是我国高校面向本科生最早的赛事之一,自2008年开赛至今,一直由教育部高校与计算机相关教指委等或独立或联合主办。大赛的目的是以赛促学、以赛促教、以赛促创,为国家培养德智体美劳全面发展的创新型、复合型、应…...

嘉定区2022年高新技术企业认定资助申报指南
各镇人民政府,街道办事处,嘉定工业区、菊园新区管委会,各相关企业: 为推进实施创新驱动发展战略,加快建设具有全球影响力的科技创新中心,根据《嘉定区关于加快本区高新技术企业发展的实施方案(…...

【C++】关键字、命名空间、输入和输出、缺省参数、函数重载
C关键字(C98)命名空间产生背景命名空间定义命名空间使用输入&输出缺省参数什么叫缺省参数缺省参数分类函数重载函数重载概念C支持函数重载的原理--名字修饰C关键字(C98) C总计63个关键字,C语言32个关键字。 下面我们先看一下C有多少关键字,不对关键…...

【一道面试题】关于HashMap的一系列问题
HashMap底层数据结构在1.7与1.8的变化 1.7是基于数组链表实现的,1.8是基于数组链表红黑树实现的,链表长度达到8时会树化 使用哈希表的好处 使用hash表是为了提升查找效率,比如我现在要在数组中查找一个A对象,在这种情况下是无法…...

论文笔记: Monocular Depth Estimation: a Review of the 2022 State of the Art
中文标题:单目深度估计:回顾2022年最先进技术 本文对比了物种最近的基于深度学习的单目深度估计方法: GPLDepth(2022)[15]: Global-Local Path Networks for Monocular Depth Estimation with Vertical CutDepthAdabins(2021)[1]: Adabins:…...
Springmvc补充配置
Controller配置总结 控制器通常通过接口定义或注解定义两种方法实现 在用接口定义写控制器时,需要去Spring配置文件中注册请求的bean;name对应请求路径,class对应处理请求的类。 <bean id"/hello" class"com.demo.Controller.HelloCo…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
