go语言的并发编程
并发编程是 Go语言的一个重要特性,而 go语言也是基于此而设计出来的。 本文将会介绍如何使用go-gc中的“runtime”方法实现 go语言中的并发编程。 在之前的文章中,我们已经对 runtime方法进行了详细介绍,这次文章将对 runtime方法进行深入分析,并讲解如何在go-gc中使用该方法。
一、准备工作
首先我们要了解一下什么是 runtime方法,以及该方法的工作原理。
首先需要声明以下三个条件:
当存在多个线程时,这些线程在一个线程中执行,如果有一个线程需要返回,则将在这个执行的线程之外的其他线程中进行;
如果没有任何一个或多个线程时需要并发地同时使用这个方法;如果有多个线程时可以将此方法用于实现一些比较复杂的操作。
然后我们来了解一下该方法使用的是什么算法:
由于 runtime不会导致程序崩溃,所以在程序运行时它就不会发生问题。所以下面我们先看一下使用 runtime算法进行程序并发执行之后的情况。

二、创建线程
创建线程
在这里我们需要使用到 runtime方法,该方法是由go-gc提供的。
如果要想用该方法创建线程,需要在go-gc中创建一个文件,此文件中将会包含有关 runtime方法的信息。
创建线程
当我们将这个文件放入到指定目录下后,程序就会开始运行了,如果此时我们想要退出的话,只需要把这个文件移动到另外一个目录即可,具体如下:
此时程序会自动退出并回到线程状态。
相关文章:

go语言的并发编程
并发编程是 Go语言的一个重要特性,而 go语言也是基于此而设计出来的。 本文将会介绍如何使用go-gc中的“runtime”方法实现 go语言中的并发编程。 在之前的文章中,我们已经对 runtime方法进行了详细介绍,这次文章将对 runtime方法进行深入分析,并讲解如何在go-gc中使用该方…...

亚马逊要求UL94防火测试阻燃测试标准及项目
UL94认证是什么?分几个等级?是如何表示各等级?带电的产品上架亚马逊都需要相关的UL报告,需要有ISO 17025资质的实验室出具的测试报告才能正常销售和恢复链接,UL94防火测试则是其中一项。UL94试验共有五种:1.B级的水平燃烧试验2.…...

ClickHouse 合并树表引擎 MergeTree 原理分析
目录 前言 MergeTree 存储 MergeTree思想 MergeTree存储结构 MergeTree查询 索引检索 数据Sampling 数据扫描 建表 数据存储...
用YOLOv8推荐的Roboflow工具来训练自己的数据集
YOLOv8是Ultralytics公司开发的YOLO目标检测和图像分割模型的最新版本,相较于之前的版本,YOLOv8可以更快速有效地识别和定位图像中的物体,以及更准确地分类它们。 作为一种深度学习技术,YOLOv8需要大量的训练数据来实现最佳性能。…...
三层交换机【实验】
目录 1、要求: 2、拓扑: 3、创建vlan和端口定义并划入vlan: 4、创建以太网中继Eth-Trunk使sw1和sw2的相互冗余并且不浪费链路: 5、使用mstp定义组和对应的根: 6、配置网关冗余: 7、核心层的路由的IP配…...
)
Anolis 8.6 部署 Kafka 3.3.1 安装和测试(二)
动态初始化Kafka消费者实例一.Kafka 环境搭建二.动态初始化消费者1.Topic定义2.方法处理器工厂3.参数解析器(Copy SpringBoot 源码)4.消费接口和消费实现5.动态初始化1.关键类简介2.动态初始化实现一.Kafka 环境搭建 参考:Kafka搭建和测试 …...

sed和awk
文章目录1、sed的简单介绍2、sed的使用方法2.1 命令行格式2.2 案例2.3 sed结合正则使用2.4 脚本格式3、awk的简单介绍4、awk的使用方法4.1 命令行模式4.2 脚本模式5、awk内部相关变量5.1 案例6、awk工作原理7、awk进阶使用8、awk脚本编程8.1 案例1、sed的简单介绍 sed是流编辑…...
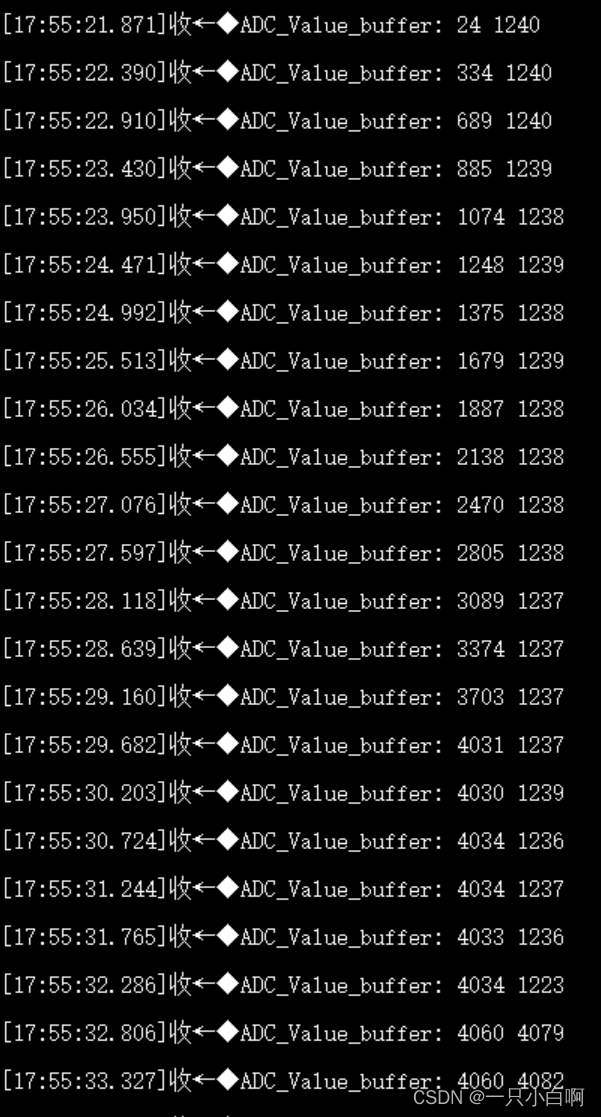
使用STM32 CUBE IDE配置STM32F7 用DMA传输多通道ADC数据
我的使用环境: 硬件:STM32F767ZGT6、串口1、ADC1、16MHz晶振、216MHz主频 软件:STM32 CUBE IDE 优点:不用定时触发采样,ADC数据是不停的实时更新,ADC数据的更新频率根据采样时钟和采样周期决定,…...
linux 学习(持续更新)
一:初识linux 新装操作环境: mac intel电脑 CentOS系统版本:CentOS-8.1.1911 在这里解释一下[chenllocalhost /]$这句话的含义: chenl是用户名,也就是你自己起的名字。 是分割的符号 localhost是主机名,也…...

Nacos【一】Nacos集群部署配置
系列文章目录 暂无 文章目录系列文章目录前言一、Nacos集群架构1.ip直连2. SLB3. 域名-SLB二、集群部署准备2.1 机器准备2.2 Nginx安装配置1.安装2.负载均衡配置2.3 nacos安装配置1.nacos节点2. MySQL准备1.Docker安装MySQL2. nacos对应数据库初始化三、 集群启动1.失败原因汇…...

“亚洲一号”也能上市?REITs背后的物流设施风起云涌
京东最近发生了两件大事,两件都与物流基础设施有关。 一件是2月8日,嘉实京东仓储物流封闭式基础设施证券投资基金(简称“京东仓储REIT”)正式登陆上交所,投资者获得了机会,去分享京东三处物流园区的收益&a…...

2023养老展,CBIAIE第十届中国北京国际老年产业博览会
8月招商季,第十届中国(北京)国际老年产业博览会再次盛大举办; CBIAIE北京国际老年产业博览会位域优势: ——北京,中国首都,世界一线城市,地处中国北部、华北平原北部,东…...
【Android -- 每日一问】现在 Android 怎么学?学什么?
不管在任何行业,任何岗位,初级技术人才总是供大于求;不管任何行业、岗位,技术过硬的也都是非常吃香的! 这几年 Android 新技术的迭代明显加速了,有来自外部跨平台新物种的冲击,有去 Java 化的商…...
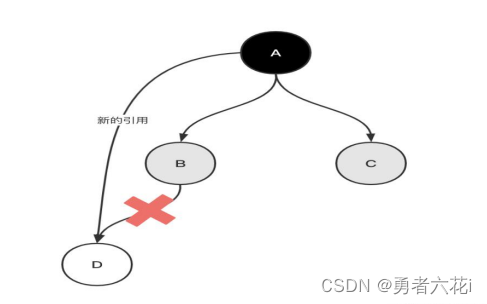
JVM垃圾回收
概述 Java是支持自动垃圾回收的,有些语言不支持自动垃圾回收(C)自动垃圾回收不是Java的首创 垃圾是什么? 在 JVM 中垃圾是指在运行程序中没有任何指针指向的对象,这个对象就是需要被回收的垃圾。 哪些区域需要回收…...

clickhouse集群安装
单机安装 yum install yum-utilsrpm --import https://repo.clickhouse.com/CLICKHOUSE-KEY.GPGyum-config-manager --add-repo https://repo.clickhouse.com/rpm/clickhouse.reposudo yum install clickhouse-server clickhouse-client 配置文件 vim /etc/clickhouse-serve…...

Zookeeper入门
Zookeeper入门概述特点结构应用场景选举机制节点信息监听原理写数据原理分布式锁概述 Zookeeper是一个开源的分布式的,为分布式框架提供协调服务的Apache项目。 Zookeeper 从设计模式的角度来开:是一个基于观察者模式设计的分布式服务管理框架…...

JavaScript
BOM核心对象docunmentBOM核心对象windowBOM包含着DOMF12即可打开浏览器控制台navigator(浏览器版本)、history(浏览器历史记录),location(地址信息)、screen(屏幕相关)JS输出形式:浏览器输出:wi…...

.gitignore 常用忽略规则
.gitignore常用忽略语法 1、空格不匹配任意文件,可作为分隔符,可用反斜杠转义 2、以井号#开头的文件标识注释,可以使用反斜杠进行转义 3、以斜杠/开头表示目录 4、以星号*通配多个字符 5、以问号?通配单个字符 6、以方括号[]包含单个字符的…...

Vue路由 —— vue-router
在上一篇内容讲到关于单页面组件的内容,同时也附上补充讲了关于单页面(SPA)和多页面(MPA)之间的优缺点,在本篇目当中就要来讲这个路由(vue-router),通过路由来实现页面的…...

Java Jackson TypeReference获取泛型类型信息【泛型】
Jackson是一个比较流行的Json序列化和反序列化框架。本文以Jackson为例介绍TypeReference实现涉及泛型的反序列化,及TyperReference的实现原理。对于获取泛型类型信息的场景,TypeReference是一个可以参考的通用解决方案。 Jackson ObjectMapper的readVa…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
