杨浦区人工智能及大数据(云计算)企业登记工作(2023年度)的通知
各相关单位:
根据《“长阳秀带”在线新经济产业集聚发展若干政策》(杨府发〔2022〕2号)及其实施细则的要求,现组织开展2023年度杨浦区人工智能与大数据(云计算)企业登记备案工作,现将相关工作通知如下:
一、登记原则
企业登记遵循“自主自愿”原则。参照《杨浦区新一代人工智能与大数据产业技术应用细分领域目录》(以下简称目录,见附件1)自主登记,不收取任何费用。
二、登记对象
在杨浦区注册并纳税登记,主营业务或产品属于目录范围,正常经营,无不良信用记录。
三、登记流程
1、提交材料:登记企业填写《杨浦区人工智能及大数据(云计算)企业登记表》(见附件2),纸质材料和电子版各一份,包含企业营业执照复印件、2022年度财务报表(2023年新注册成立的企业填写申报前一月的财务情况)、相关技术应用领域知识产权证书、软件著作权登记证书、其他资质认证复印件等其他证明材料。
2、登记流程:由户管单位初审盖章后交区科委审核(户管单位联系方式见附件3),并在上海数字产业运行系统内登记注册,完整填写企业基本情况信息及上年度经济运行数据(新注册企业填报申报时间前一个月份的财务数据)。
3、登记时间:登记备案工作长期受理,首批次于6月底截止,第二批于11月底截止,成功登记的企业名单由区科委报联审小组审议通过后分批次公示。
登记受理单位:杨浦区科学技术委员会;
联系人:奚老师
材料寄送地址:杨浦区惠民路800号2号楼1403室
附件:
1.《杨浦区人工智能与大数据产业技术应用细分领域目录》
2.《杨浦区人工智能与大数据(云计算)企业登记表》
3.《杨浦区主要户管单位联系方式》
杨浦区科学技术委员会
2023年2月7日
相关文章:
企业登记工作(2023年度)的通知)
杨浦区人工智能及大数据(云计算)企业登记工作(2023年度)的通知
各相关单位: 根据《“长阳秀带”在线新经济产业集聚发展若干政策》(杨府发〔2022〕2号)及其实施细则的要求,现组织开展2023年度杨浦区人工智能与大数据(云计算)企业登记备案工作,现将相关工作通知如下: 一…...

2023年去培训机构学前端还是Java?
选择专业肯定是优先考虑更有发展前景和钱途的专业。毕竟IT专业的培训费都不低,基本都要一两万左右,咱们花钱总是希望获得最大回报。 那么到底哪个更有发展前景呢? 零基础能学得会吗? 就业薪资如何呢? 前言 不知道大家有…...

【React】组件事件
React(二) 创建组件 函数组件 函数组件:使用JS的函数或者箭头函数创建的组件 使用 JS 的函数(或箭头函数)创建的组件,叫做函数组件约定1:函数名称必须以大写字母开头,React 据此区分组件和普通的 HTML约定2:函数组…...

黑/白盒测试说明
白盒测试白盒测试也称结构测试或逻辑驱动测试,它是按照程序内部的结构测试程序,通过测试来检测产品内部动作是否按照设计规格说明书的规定正常进行,检验程序中的每条通路是否都能按预定要求正确工作。白盒测试的测试方法有代码检查法、静态结…...

车道线检测-Eigenlanes 论文学习笔记
论文:《Eigenlanes: Data-Driven Lane Descriptors for Structurally Diverse Lanes》 代码:https://github.com/dongkwonjin/Eigenlanes 核心:在 Eigenlane Space 中检测车道线 创新点 Eigenlane:数据驱动的车道描述符ÿ…...

docker run mysql -e 的环境变量 Environment Variables
例子 sudo docker run -itd --name DockerMysqlLatest3307 -p 3307:3306 -e MYSQL_ROOT_PASSWORDroot的密码 mysql:latest### root无密码 sudo docker run -itd --name Mysql57 -p 57:3306 -e MYSQL_ALLOW_EMPTY_PASSWORDroot mysql:5.7https://hub.docker.com/_/mysql?tabde…...

第17章 MongoDB 条件操作符教程
第17章 MongoDB 条件操作符教程 描述 条件操作符用于比较两个表达式并从mongoDB集合中获取数据。 在本章节中,咱们将讨论如何在MongoDB中使用条件操作符。 MongoDB中条件操作符有: (>) 大于 - $gt(<) 小于 - $lt(>) 大于等于 - $gte(< …...
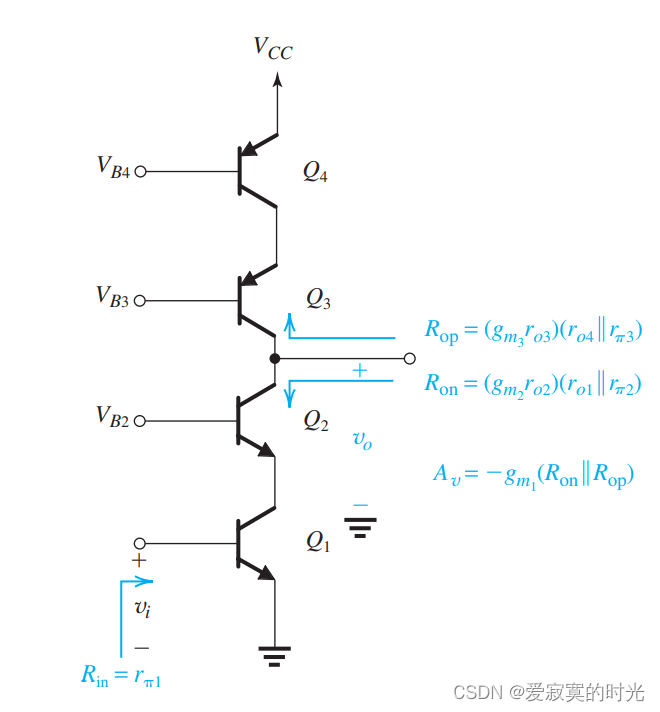
电子技术——共源共栅放大器
电子技术——共源共栅放大器 之前我们提到过,提高基础增益单元(共源放大器)的一种方法是提高其 ror_oro 的阻值,之后我们学过共栅放大器作为电流缓冲器可以做到这一点,自然地我们就得到了终极解决方案,也…...
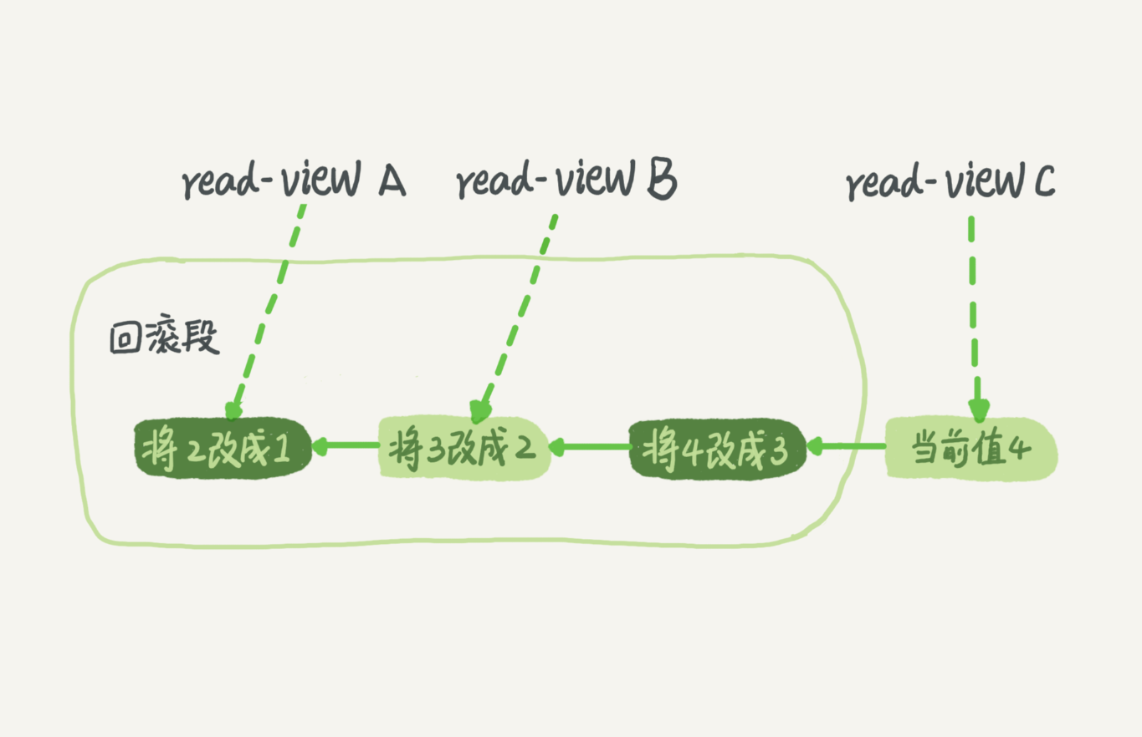
《MySQL学习》 事务隔离 与 MVCC
《MySQL学习》 事务隔离 一.事务的概念 事务保证一组数据要么全部成功要么全部失败,MySQL的事务基于引擎(如InnoDB)实现。 二.事务的隔离性与隔离级别 MySQL的标准隔离级别: 读未提交 : 一个事务还没提交时&#…...
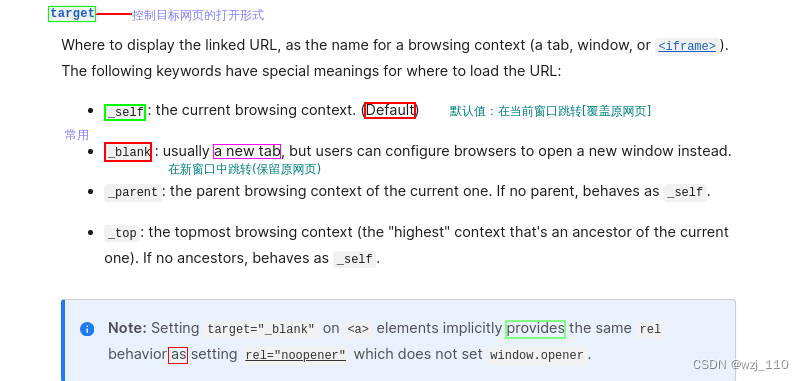
html(二)基础标签
一 HTML中的注释 重点: 在哪写注释? 注释的形式? vs code和webstorm都可以通过 ctrl / 进行单行注释和取消注释 ① html中注释的形式 1) html文档中单行和多行注释是"<!-- -->" -->html2) 在html文档中,script标签…...
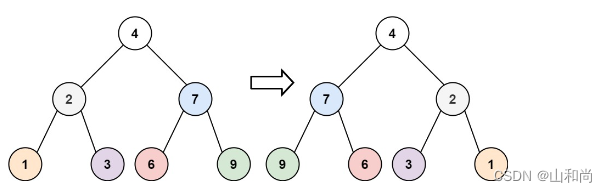
leetcode刷题---递归思想
leetcode刷题---递归思想)1.1 递归介绍1.2 基本步骤1.3 代表题目1.3.1 入门题---青蛙跳1.3.2.1 初级题226.翻转二叉树112.路径总和1.3.3 中级题---汉诺塔问题1.3.4 进阶题---细胞分裂1.1 递归介绍 如果在函数中存在着调用函数本身的情况,这种现象就叫递…...
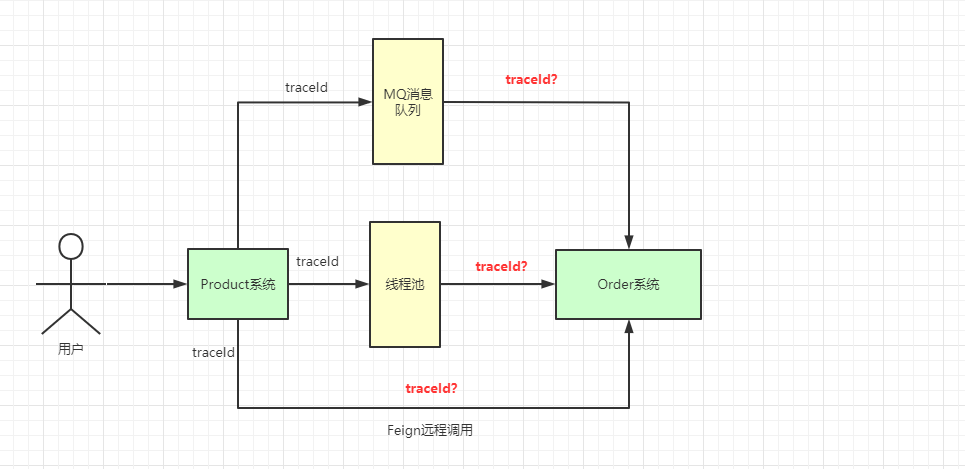
ThreadLocal 源码级别详解
ThreadLocal简介 稍微翻译一下: ThreadLocal提供线程局部变量。这些变量与正常的变量不同,因为每一个线程在访问ThreadLocal实例的时候(通过其get或set方法)都有自己的、独立初始化的变量副本。ThreadLocal实例通常是类中的私有静…...

训练营day17
110.平衡二叉树 力扣题目链接 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。 示例 1: 给定二叉树 [3,9,20,null,null,15,7] 返回 true 。 示…...
Nodejs原型链污染
Nodejs与JavaScript和JSON 有一些人在学习JavaScript时会分不清Nodejs和JavaScript之间的区别,如果没有node,那么我们的JavaScript代码则由浏览器中的JavaScript解析器进行解析。几乎所有的浏览器都配备了JavaScript的解析功能(最出名的就是…...

【Vue3】element-plus中el-tree的递归处理赋值回显问题
目录一:先获取所有权限tree二:在获取所有该角色能有的权限tree三:递归处理勾选tree节点由于项目是从0-1开始构建的 rbac都需要重新构建对接 所以涉及到了权限管理和菜单管理 一级菜单包含多个二级菜单 若二级不全选,则一级显示 半…...

C语言---宏
专栏:C语言 个人主页:HaiFan. 专栏简介:本专栏主要更新一些C语言的基础知识,也会实现一些小游戏和通讯录,学时管理系统之类的,有兴趣的朋友可以关注一下。 #define预处理预定义符号define#define定义标识符…...

算法导论—路径算法总结
图算法 单源最短路径 Bellman-Ford算法: 顶点为V,边为E的图 对每条边松弛|V|-1次边权可以为负值若存在一个可以从源结点到达的权值为负值的环路,算法返回False时间复杂度:O(VE) 有向无环图单源最短路径 DAG-SHORTEST-PATHS …...

程序环境--翻译+执行
ANSI C标准下,有两种程序环境。 第1种是翻译环境,在这个环境中源代码被转换为可执行的机器指令。 翻译环境包括:预处理(预编译)编译汇编链接。四个步骤。 第2种是执行/运行环境,它用于实际执行代码。 链接…...

微信小程序内部那些事
微信小程序没有window、document,它更像是一个类似 Node.js 的宿主环境。因此在小程序内部不能使用 document.querySelector 这样的选择器,也不支持 XMLHttpRequest、location、localStorage 等浏览器 API,只能使用小程序自己提供的 API&…...

这是从零在独自开开发,将是副业赚钱最好的平台!
文章目录最重要的事情放前面1.前言2.简单介绍一下3.【独自开】介绍3.1 分层标准化平台架构3.2 集成第三方数字接口3.3 支持各个行业的系统定制开发4.如何在【独自开】赚钱获取收益?4.1 如何称为【独自开】开发者?最重要的事情放前面 通过平台的审核也可以得到相应的奖金&…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
