矩阵理论复习(十二)
已知方阵A的不变因子:
- 求谱半径
- 求矩阵级数
- 判断矩阵幂级数的收敛性

若矩阵B的某个算子范数小于1,则I-B可逆。
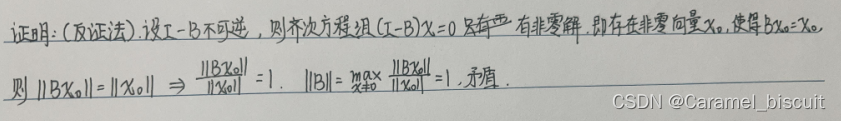


矩阵分析


任何相容矩阵范数都存在与之相容的向量范数。
盖尔圆盘定理一的证明

椭圆范数的证明
若||.||是Cm上的向量范数,A为列满秩矩阵,则||A.||是Cn上的向量范数。

椭圆范数的应用
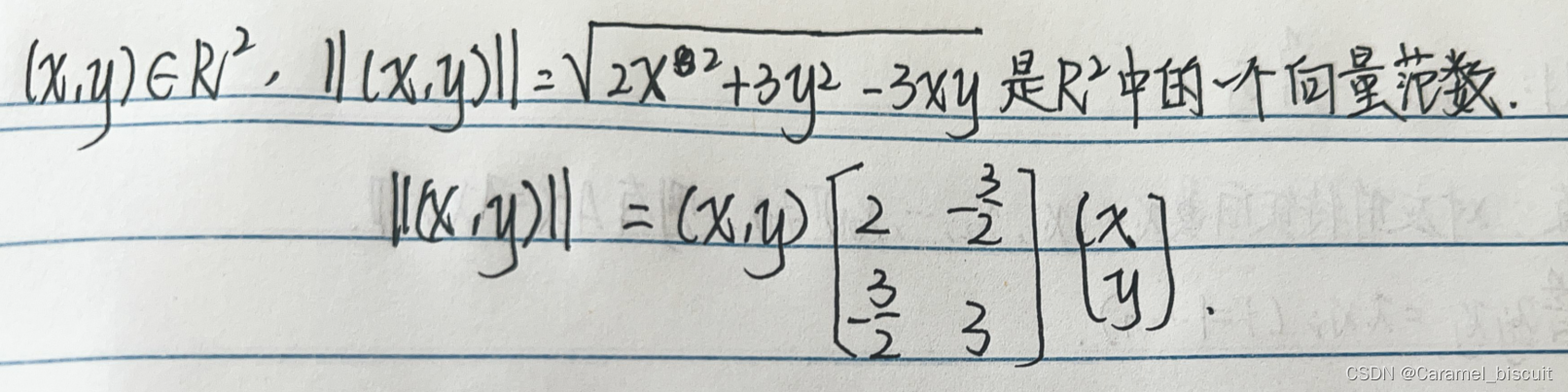
Rayleigh商
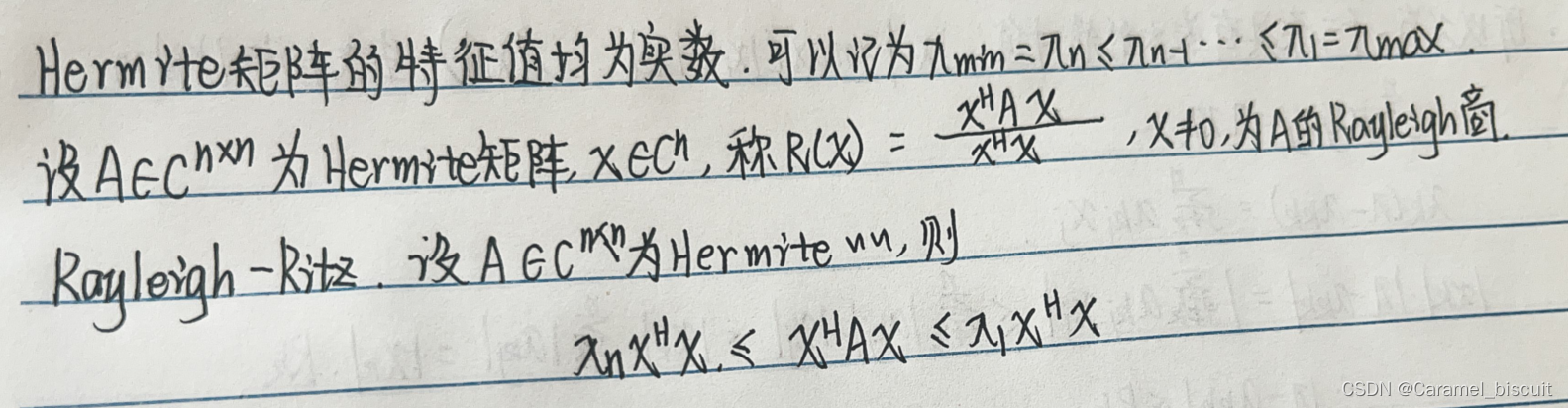
R(A+)=R(AH)
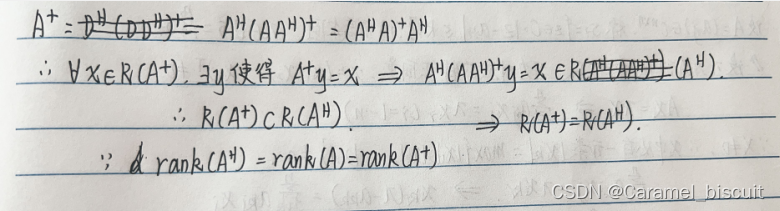
A+=AH(AAH)+=(AHA)+AH
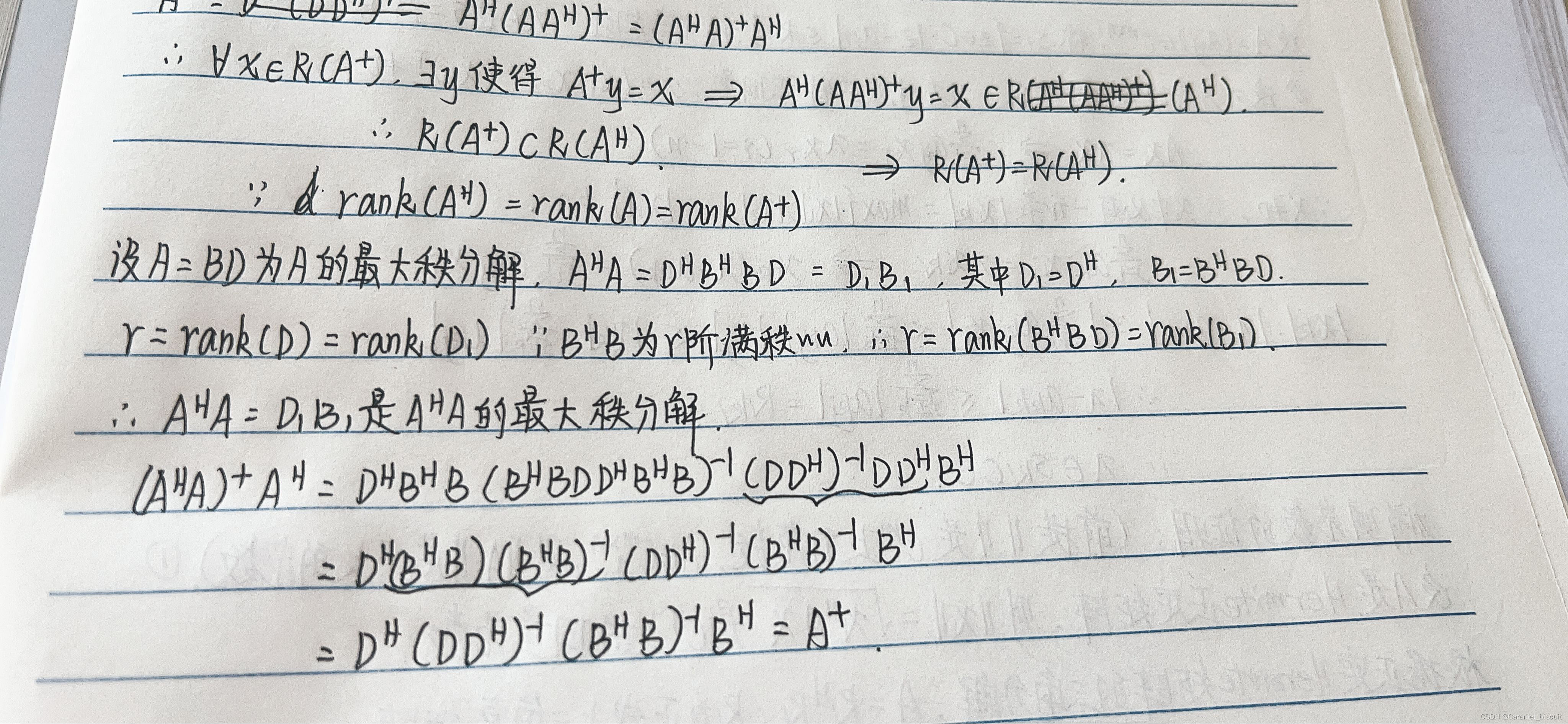
当A的某算子范数小于1时,证明E-A可逆

证明自反广义逆
- AGA=A
- rank(G)=rank(A)
证明G=YZ是A的自反广义逆

B=[A+ A+]

设T是线性空间V上的投影,则投影的值域和核互为直和补。

维数定理

直和
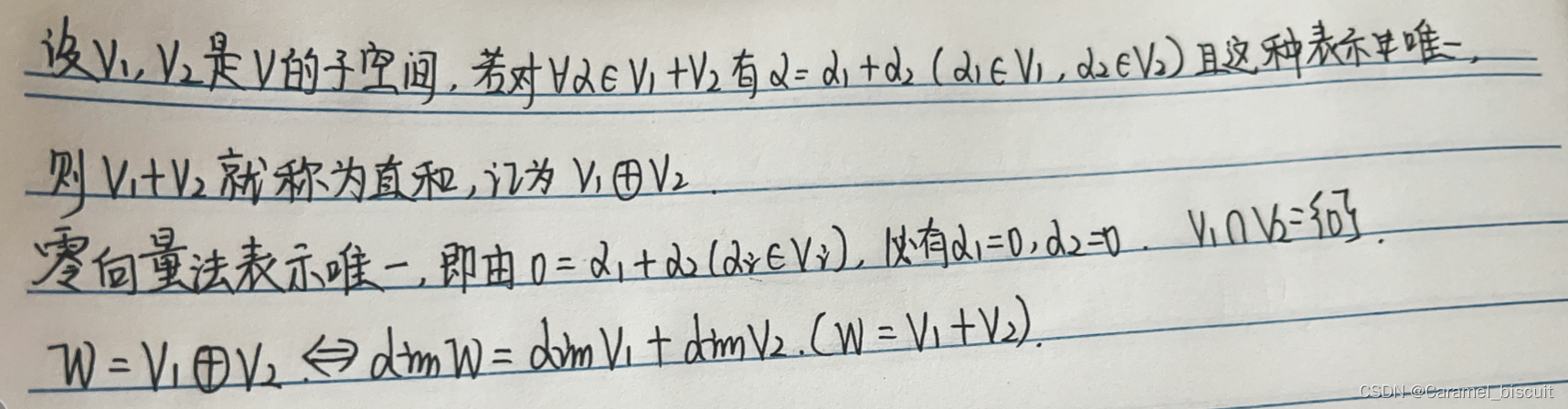
正规矩阵A的特征值的模等于A的奇异值
rank(A)=rank(AH)=rank((AHA)=rank((AAH)

三角矩阵的结论
- 上三角矩阵的逆仍是上三角矩阵,且对角元是R对角元的倒数。
- 两个上三角矩阵的乘积仍是上三角矩阵,且对角元是R1,R2对角元的乘积。
- 酉矩阵的逆还是酉矩阵,酉矩阵的乘积仍是酉矩阵。
相关文章:

矩阵理论复习(十二)
已知方阵A的不变因子: 求谱半径求矩阵级数判断矩阵幂级数的收敛性 若矩阵B的某个算子范数小于1,则I-B可逆。 矩阵分析 任何相容矩阵范数都存在与之相容的向量范数。 盖尔圆盘定理一的证明 椭圆范数的证明 若||.||是Cm上的向量范数,A为…...
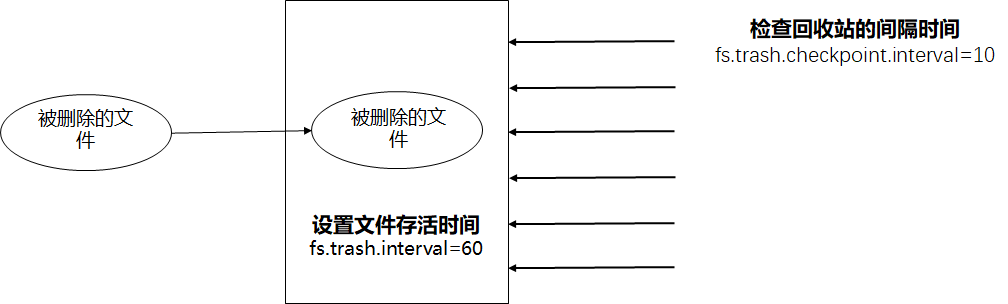
大数据框架之Hadoop:HDFS(七)HDFS 2.X新特性
7.1集群间数据拷贝 scp实现两个远程主机之间的文件复制 scp -r hello.txt roothadoop103:/root/hello.txt // 推 push scp -r roothadoop103:/root/hello.txt hello.txt // 拉 pull scp -r roothadoop103:/root/hello.txt roothadoop104:/root //是通过本地主机中…...
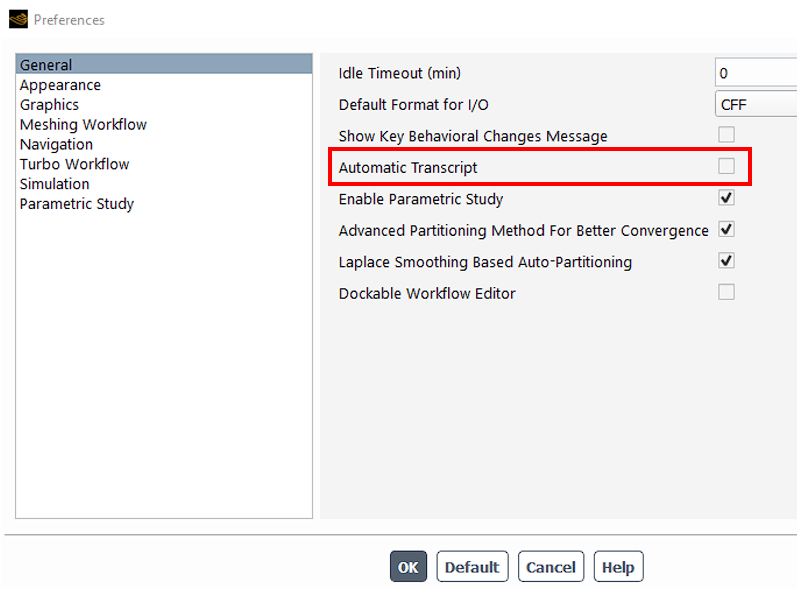
Fluent工作目录
1 工作目录定义工作目录(working directory)是一种文件存储路径设置方式。基于工作目录的方法,写文件时只需要指定文件名,而不需要指定完全的文件路径,从而简化程序编写,对不同操作系统环境有更好的适应性。…...

Learning C++ No.10【STL No.2】
引言: 北京时间:2023/2/14/23:18,放假两个月,没有锻炼,今天去跑了几圈,一个字,累,感觉人都要原地升天了,所以各位小伙伴,准确的说是各位卷王,一定…...
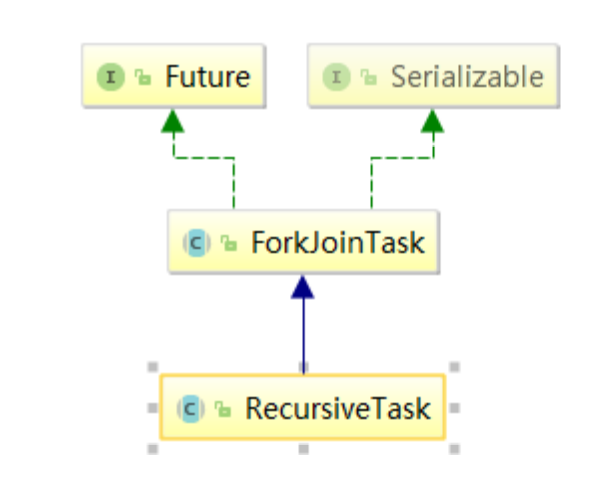
【java 高并发编程之JUC】2w字带你JUC从入门到精通
点击查看脑图目录地址,实时更新 1 什么是 JUC 1.1 JUC 简介 在 Java 中,线程部分是一个重点,本篇文章说的 JUC 也是关于线程的。JUC 就是 java.util .concurrent 工具包的简称。这是一个处理线程的工具包,JDK 1.5 开始出现的。 1.2 进程与…...
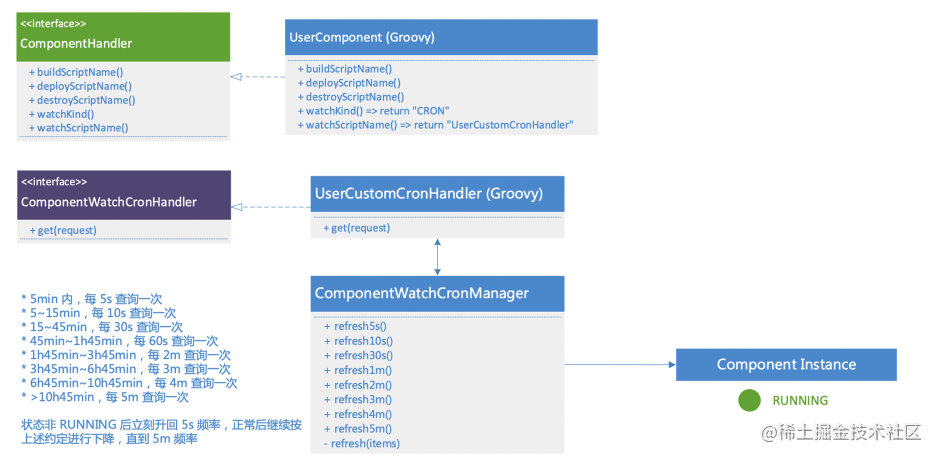
QCon演讲实录(下):多云管理关键能力实现与解析-AppManager
在上篇中,我们已经基本了解了多云管理。现在,我们将深入探讨多云管理关键能力实现:AppManager。 什么是AppManager? 上面我们讲了理论、我们自己使用的交付流程和整体架构,下面我们进入关键能力实现与解析的环节&…...

刚刚退出了一个群,关于在要麒麟OS上运行Labview
年龄过了45,看问题,与以前不太一样了。 觉得浪费时间的事,宁可发呆,也不会参和。 竟然一个群里在讨论如何满足客户的需求:麒麟OS上运行Labview。 然后直接退了群。 这种问题,我觉得可能 发在csdn上&…...

el-uploader 文件上传后,又被修改,无法提交到后端 ERR_UPLOAD_FILE_CHANGED
problem 文件上传后,又被修改,无法提交到后端 具体步骤: 文件上传本地文件打开并修改保存提交ajax 这个问题不仅仅局限于el-uploader,是一个普遍性的问题 导致的问题 问题1:提交请求时,控制台报错 net…...

利用Eigen实现点云体素滤波
目录 前言 一、算法原理 二、代码实现 1.头文件 2.源文件 三、效果展示 前言 体素滤波原理简单,是常用的...

linux高级命令之多进程的使用
多进程的使用学习目标能够使用多进程完成多任务1 导入进程包#导入进程包import multiprocessing2. Process进程类的说明Process([group [, target [, name [, args [, kwargs]]]]])group:指定进程组,目前只能使用Nonetarget:执行的目标任务名…...

CSS 圆角边框 盒子阴影 文字阴影
目录 1.圆角边框(重点) 2.盒子阴影(box-shadow) 3.文字阴影(text-shadow) 1.圆角边框(重点) border-radius 属性用于设置元素的外边框圆角。 语法: border-radius: l…...

python简单解析打印onnx模型信息
当我们加载了一个ONNX之后,我们获得的就是一个ModelProto,它包含了一些版本信息,生产者信息和一个GraphProto。在GraphProto里面又包含了四个repeated数组,它们分别是node(NodeProto类型),input(ValueInfoProto类型)&a…...
UE4 编写着色器以及各种宏的理解
参考链接:如何为 UE4 添加全局着色器(Global Shaders) - Unreal Enginehttps://docs.unrealengine.com/5.1/zh-CN/adding-global-shaders-to-unreal-engine/如何为 UE4 添加全局着色器(Global Shaders) - Unreal Engin…...

小笔记:Python 使用字符串调用函数
小笔记:Python中如何使用字符串调用函数/方法?jcLee95:https://blog.csdn.net/qq_28550263?spm1001.2101.3001.5343 本文地址:https://blog.csdn.net/qq_28550263/article/details/111874476 邮箱 :291148484163.co…...

红黑树的原理+实现
文章目录红黑树定义性质红黑树的插入动态效果演示代码测试红黑树红黑树 定义 红黑树是一个近似平衡的搜索树,关于近似平衡主要体现在最长路径小于最短路径的两倍(我认为这是红黑树核心原则),为了达到这个原则,红黑树所…...
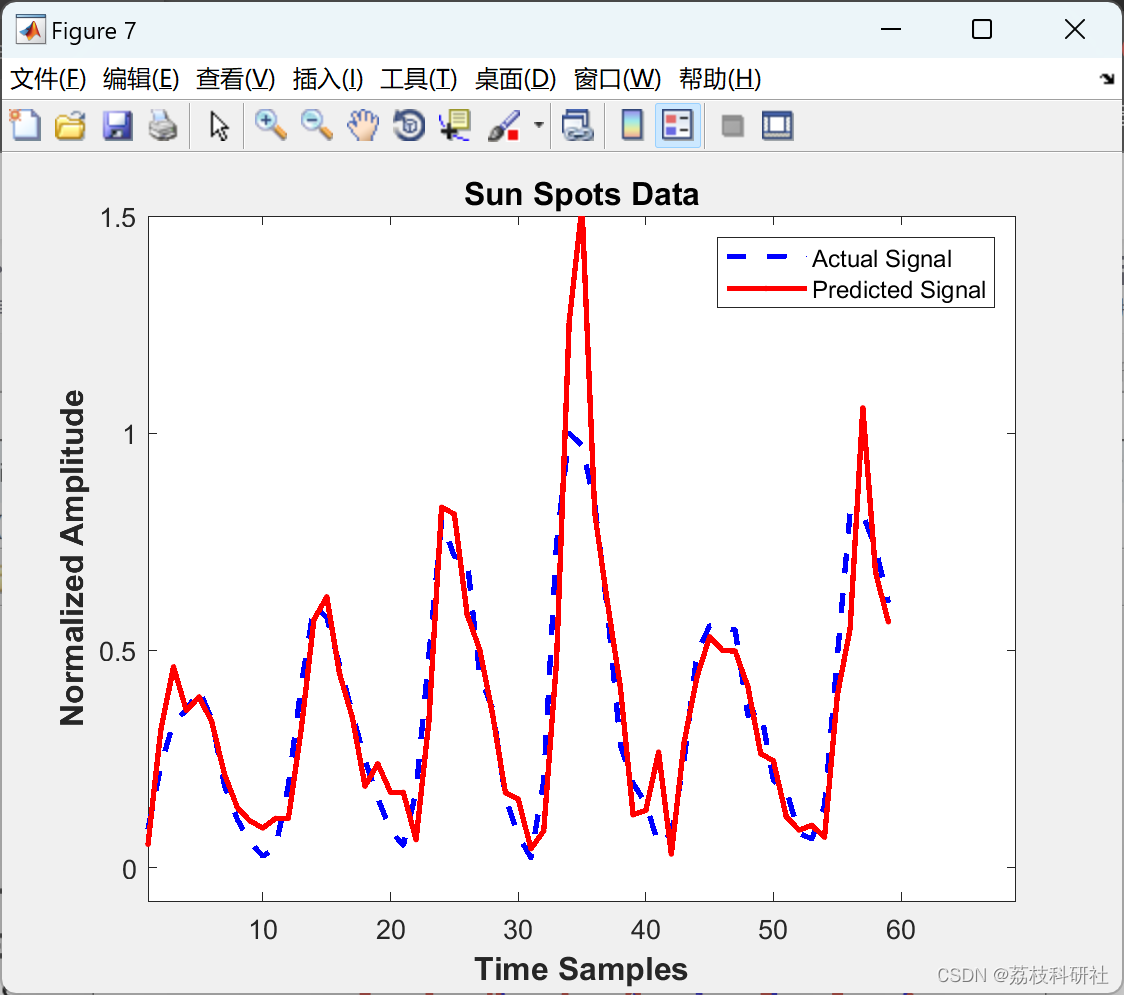
用于非线性时间序列预测的稀疏局部线性和邻域嵌入(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

使用 Vue3 重构 Vue2 项目
目录前言:一、项目整体效果展示二、项目下载使用方法三、为什么要重构项目四、重构的流程五、步骤中的 bug 以及解决方式六、未解决的问题总结:前言: 2020年9月18日,vue3正式版发布了,前几天学习完成后,我决…...
Hive学习——单机版Hive的安装
目录 一、基本概念 (一)什么是Hive (二)优势和特点 (三)Hive元数据管理 二、Hive环境搭建 1.自动安装脚本 2./opt/soft/hive312/conf目录下创建hive配置文件hive-site.xml 3.拷贝一个jar包到hive下面的lib目录下 4.删除hive的guava,拷贝hadoop下的guava 5…...
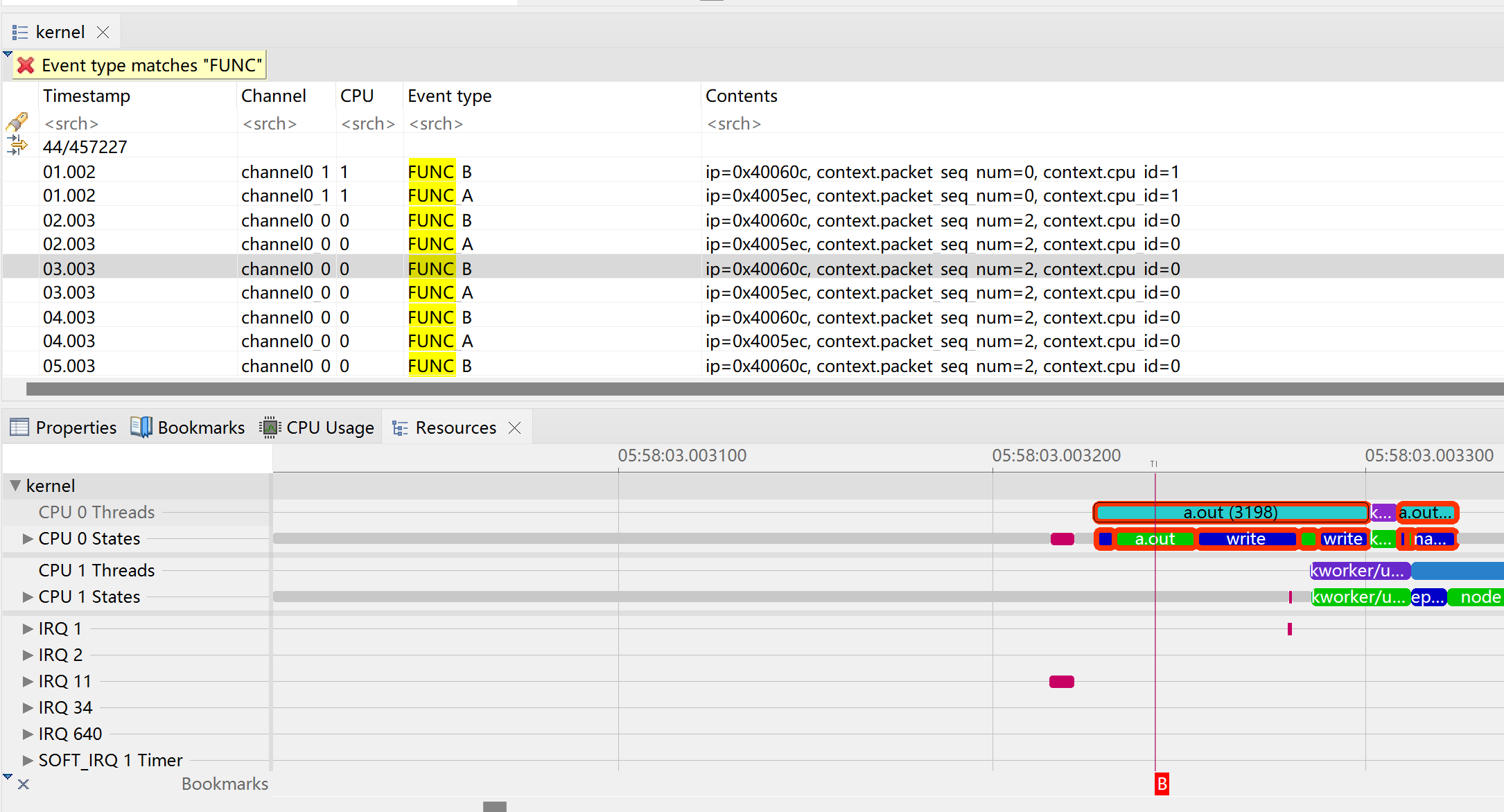
uprobe 实战
观测数据源 目前按照我的理解,和trace相关的常用数据源–探针 大致分为四类。 内核 Trace point kprobe 用户程序 USDT uprobe 在用户程序中,USDT是所谓的静态Tracepoint。和内核代码中的Trace point类似。实现方式是在代码开发时,使用USDT…...
| 真题+思路+考点+代码+岗位)
华为OD机试 - 求最大数字(Python)| 真题+思路+考点+代码+岗位
求最大数字 题目 给定一个由纯数字组成以字符串表示的数值,现要求字符串中的每个数字最多只能出现2次,超过的需要进行删除;删除某个重复的数字后,其它数字相对位置保持不变。 如34533,数字3重复超过2次,需要删除其中一个3,删除第一个3后获得最大数值4533 请返回经过删…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
