数据在内存中的存储

目录
一、数据类型的介绍
1.C语言基本内置类型
2.类型基本归类
1.整形
2.浮点型
3.构造类型
4.指针类型
二、整形在内存中的存储
三、浮点数在内次中的存储
1.存储形式
2.对M、E的特殊规定
(1)对M的特殊规定
(2)对E的特殊规定
(3)将浮点数取出内存
3.浮点数存储举例
故事很长,就当做一次长跑吧
一、数据类型的介绍
1.C语言基本内置类型

2.类型基本归类
可以分为4大类:整形、浮点型、构造类型、指针类型
1.整形

2.浮点型
float
double
3.构造类型
> 数组类型
> 结构体类型 struct
> 枚举类型 enum
> 联合类型 union
4.指针类型
int *pi;
char *pc;
float* pf;
void* pv;
二、整形在内存中的存储
变量的创建是要在内存中开辟空间的。空间的大小是根据不同的类型而决定的。操作系统会为整形变量在内存中分配4个字节,那么如何将整形变量存入呢
计算机中的整数有三种2进制表示方法,即原码、反码和补码。
 三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位 正数的原、反、补码都相同。
三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位 正数的原、反、补码都相同。
负整数的三种表示方法各不相同
原码 直接将数值按照正负数的形式翻译成二进制就可以得到原码。
反码 将原码的符号位不变,其他位依次按位取反就可以得到反码
补码 将反码加1就可以得到补码

这32个bit(4个字节)按一定的顺序存入内存
至于整型的32个bit位(4个字节)在内存中是如何存储的,请看计算机的大小端存储模式(计算机小白必看!)
三、浮点数在内次中的存储
1.存储形式
浮点数在内存中也是以二进制的形式存储的,不过小数部分的二进制表示形式与整数部分的二进制表示形式不同,并且浮点型的数据在内存中的存储方式也没有整形那么简单,其中有一些复杂的规则,不过弄清楚后就没有那么难了
小数部分的二进制表示规则,例如5.625的小数部分如何表示

整数部分的101表示十进制中的5
则5.625可以表示为101.101,并且101.101可以写成1.01101*2^2
于是国际标准IEEE(电气和电子工程协会) 754规定一个浮点数可以统一写成 (-1)^S * M * 2^E,其中(-1)^S表示这个浮点数的正负,当S=0时,表示这个浮点数为正值;S=1表示这个浮点数为负值。M表示有效数字,大于等于1,小于2,上例中有效数字M就是1.01101。2^E表示指数位,上例中E=2。如图所示
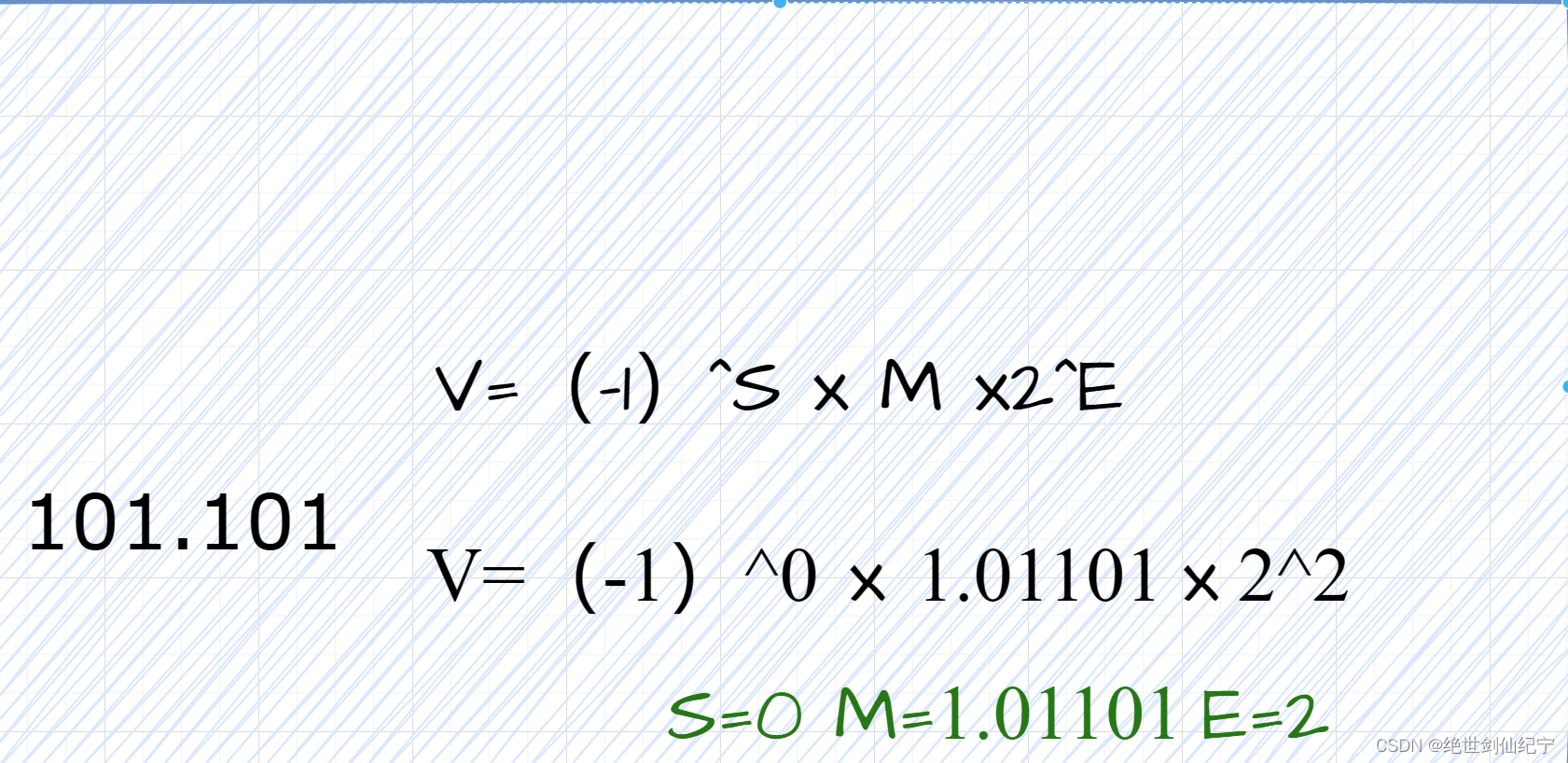
754还统一对S、E、M在内存中的大小及存储的位置进行了规定
在float类型中,第1位为符号位,接着8个bit位存储E指数位,最后23个bie位存储有效数字
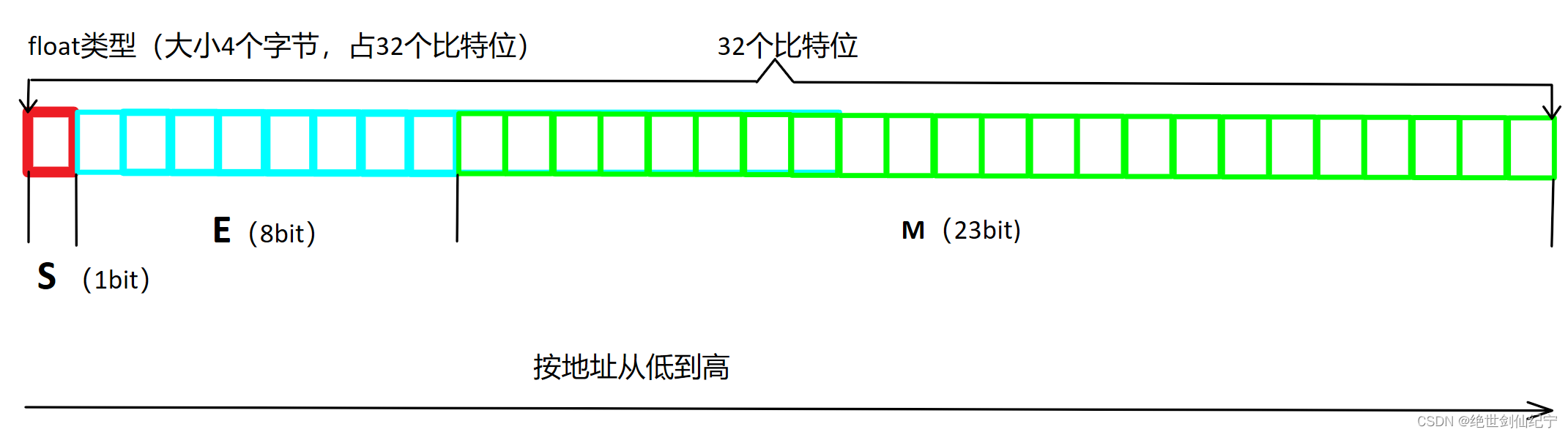
在double类型中,第一位为符号位,接着11个biet位存储E指数位,最后52个bit位存储有效数字
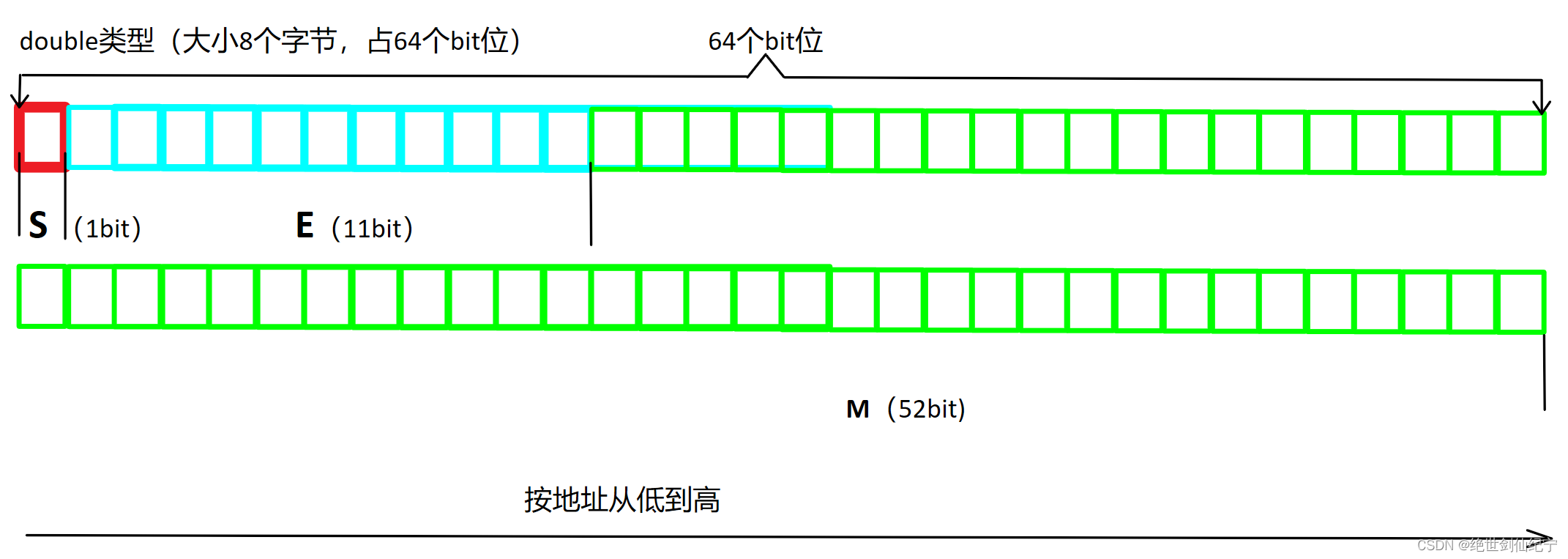
2.对M、E的特殊规定
IEEE 754对有效数字M和指数E,还有一些特别规定。
(1)对M的特殊规定
对M,前面说过, 1≤M<2 ,也就是说,M可以写成 1.xxxxxx 的形式,其中xxxxxx表示小数部分。 IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的 xxxxxx部分。比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位 浮点数为例,留给M只有23位, 将第一位的1舍去以后,等于可以保存24位有效数字。
(2)对E的特殊规定
1.将E存入内存
首先,E为一个无符号整数(unsigned int) 这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间 数是1023。比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即 10001001
如,现在将上面的5.625存入内存中
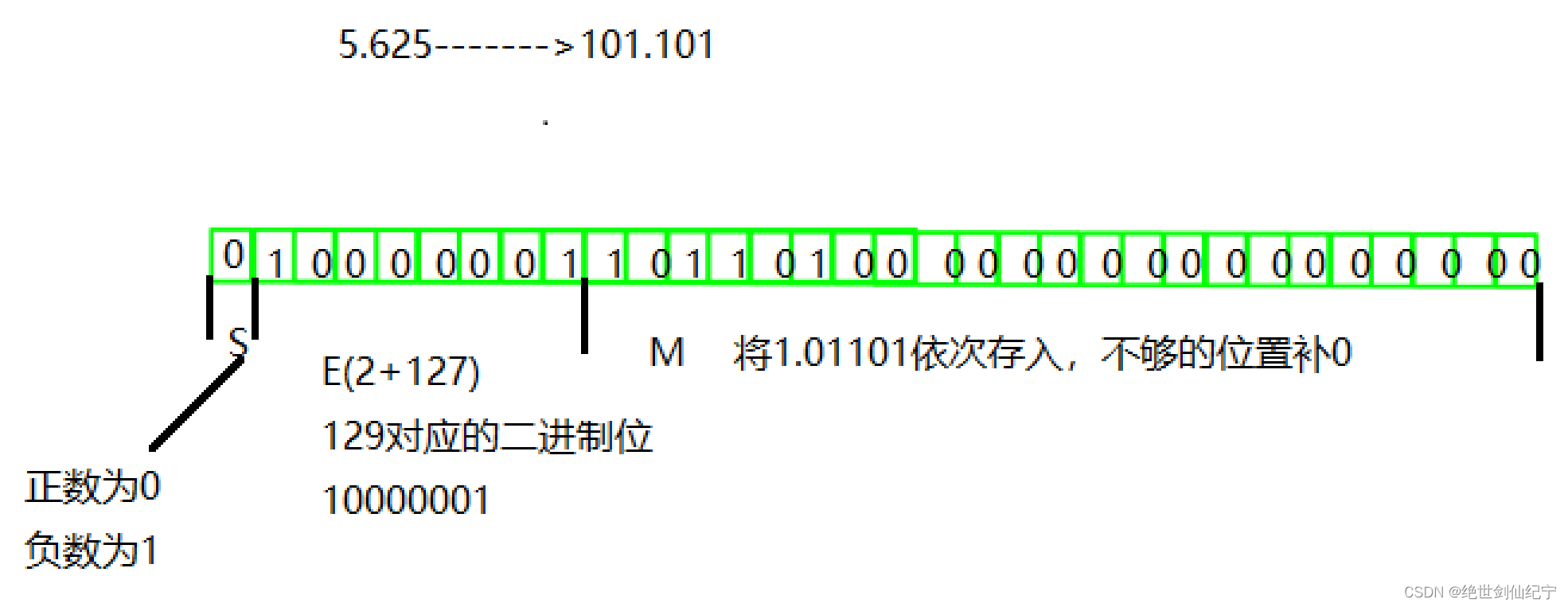
(3)将浮点数取出内存
将E加上127/1023存入内存后,在使用时要将E、M再取出来,但E的情况不同取出的方法不同
1.在一般情况下
将指数E的计算值减去127(或1023),得到真实值,再将 有效数字M前加上第一位的1
比如:
0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为 1.0*2^(-1),其阶码为-1+127=126,表示为
01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进 制表示形式为:0 01111110 00000000000000000000000
2.E为全0
当存储E时,如果加上127/1023后,E的值恰好为全0,说明E的初值为-127/-1023,且E为指数位,说明原来的数是一个很小的数,这时候取出浮点数的方法就改变了:
有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于 0的很小的数字
3.E为全1
当存储E时,如果加上127/1023后,E的值恰好为全1,说明E的初值为一个很大很大的数。这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s)
3.浮点数存储举例
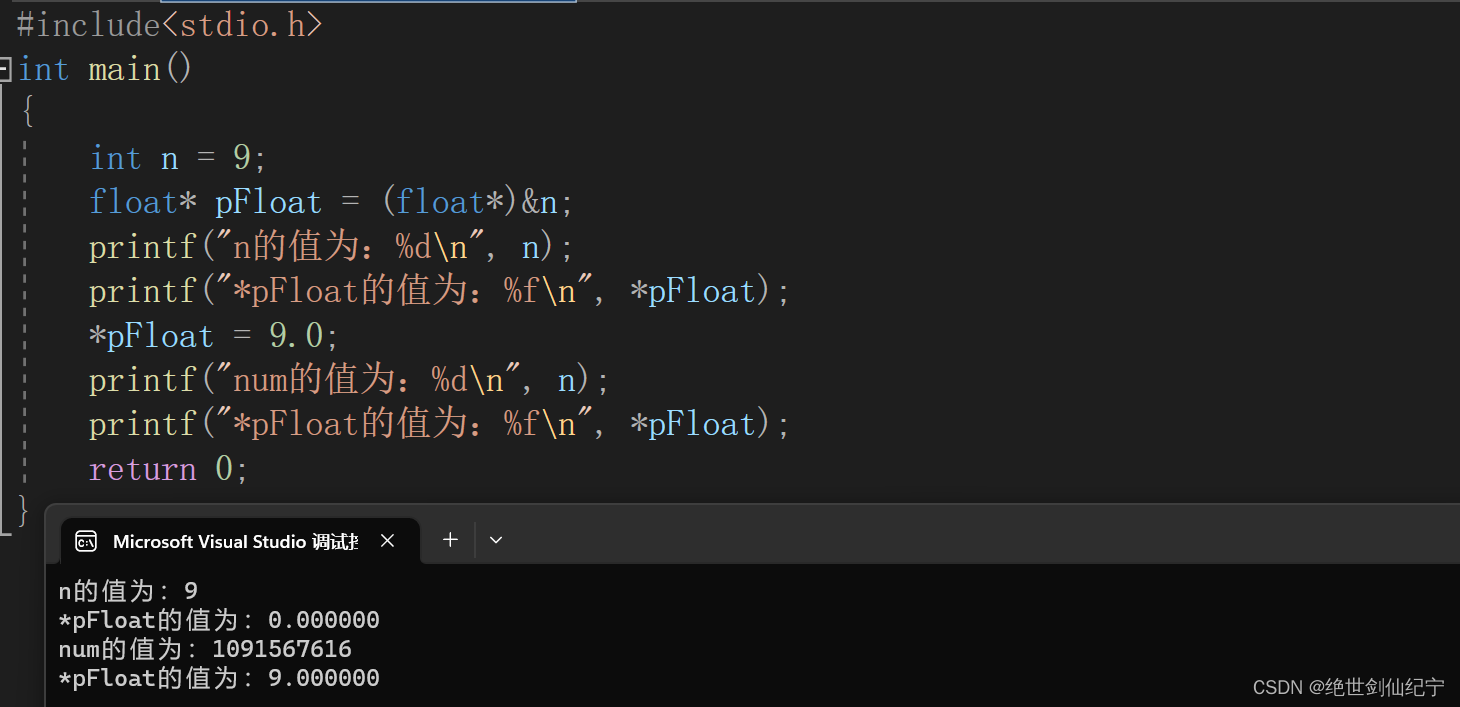 1.为什么第二个打印的是0.000000
1.为什么第二个打印的是0.000000
将9写成16进制的形式,即0x00000009,将 0x00000009 拆分,得到第一位符号位S=0,后面8位的指数 E=00000000 , 最后23位的有效数字M=000 0000 0000 0000 0000 1001,因为E为全0,符合将浮点数取出时E的形式,因此整数9改为浮点数V=9就写成
V=(-1)^0 × 0.00000000000000000001001×2^(-126)=1.001×2^(-146)
显然,V是一个很小的接近于0的正数,所以用十进制小数表示就是0.000000
2.将指针指向的值改为9.0后,为什么再以整形方式打印却成了1091567616如此大的数
当9.0本来就是浮点数时,浮点数9.0等于二进制的1001.0,即1.001×2^3。
9.0 -> 1001.0 ->(-1)^01.0012^3 -> S=0, M=1.001,E=3+127=130
那么,第一位的符号位s=0,有效数字M等于001后面再加20个0,凑满23位,指数E等于3+127=130, 即10000010
再次将它作为2进制取出内存:即M*E再转化为2进制
1.001*2^23转化为二进制
0 10000010 001 0000 0000 0000 0000 0000
 将这个二进制转化为10进制,正是1091567616
将这个二进制转化为10进制,正是1091567616
这个例子可以让我们弄懂浮点数到底在内存中是咋存的,但是更重要的是提醒我们不能随便进行强制类型转化

本文收录于青花雾气-计算机基础 ,专栏内容正在免费更新中
相关文章:

数据在内存中的存储
目录 一、数据类型的介绍 1.C语言基本内置类型 2.类型基本归类 1.整形 2.浮点型 3.构造类型 4.指针类型 二、整形在内存中的存储 三、浮点数在内次中的存储 1.存储形式 2.对M、E的特殊规定 (1)对M的特殊规定 (2)对E的…...

Rust in Action笔记 第三章 复合数据类型
通过#[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZI50wIh1-1685693144796)(null)]),不带感叹号的#[allow]仅为下一行代码提供属性,属性有多种分类,文中出现的allow属性称为诊断属性(Diag…...

算法基础学习笔记——⑬高斯消元\组合计数\容斥原理
✨博主:命运之光 ✨专栏:算法基础学习 目录 ✨高斯消元 ✨组合计数 🍓通过预处理逆元的方式求组合数: 🍓Lucas定理: 🍓分解质因数法求组合数: 前言:算法学习笔记记录日常分享,需…...
渗透测试辅助工具箱
0x01 说明 渗透测试辅助工具箱 运行条件:jdk8 双击即可运行 反弹shell,命令生成器,自动编码,输入对应IP端口即可,实现一劳永逸,集成一些小工具,辅助渗透,提高效率 输入框说明 L…...

chatgpt赋能python:Python后退命令:如何让你的程序退回到之前的状态
Python后退命令:如何让你的程序退回到之前的状态 Python是一种高级编程语言,因其易读易懂而闻名于世。Python中有很多命令用于编写程序,其中一项重要的命令是后退命令。本文将介绍Python后退命令的使用方法,并为您提供详细的步骤…...

OJ练习第127题——统计范围内的元音字符串数
统计范围内的元音字符串数 力扣链接:2559. 统计范围内的元音字符串数 题目描述 给你一个下标从 0 开始的字符串数组 words 以及一个二维整数数组 queries 。 每个查询 queries[i] [li, ri] 会要求我们统计在 words 中下标在 li 到 ri 范围内(包含 这…...
图片优化: CssSprites与Base64编码
文章目录 1 css sprites1.1 CSS Sprites是什么1.2 为什么需要css sprites1.3 优势1.4 使用原理1.5 DEMO 2 图片Base64编码 1 css sprites 1.1 CSS Sprites是什么 CSS Sprites是一种网页图片应用处理方式。 又被解释为: CSS精灵CSS图像拼合CSS贴图定位CSS图片精灵…...

JavaScript中的Map、WeakMap和Object的区别
Map Map是一种新的数据结构,它允许使用任何数据类型(包括对象和基本数据类型)作为键。 Map的一些特性包括: 保持键的插入顺序:当遍历Map时,键值对会按照插入顺序返回。键可以是任意类型:与Obj…...

华为OD机试之打印机队列(Java源码)
打印机队列 题目描述 有5台打印机打印文件,每台打印机有自己的待打印队列。 因为打印的文件内容有轻重缓急之分,所以队列中的文件有1~10不同的代先级,其中 数字越大优先级越高 打印机会从自己的待打印队列中选择优先级最高的文件来打印。 如…...

分享一个国内免费的ChatGPT网站,手机电脑通用,免费无限制,支持AI绘画
背景 ChatGPT作为一种基于人工智能技术的自然语言处理工具,近期的热度直接沸腾🌋。 作为一个AI爱好者,翻遍了各大基于ChatGPT的网站,终于找到一个免费!免登陆!手机电脑通用!国内可直接对话的C…...

【面向对象编程1】——类和对象——如桃花来
目录索引 面向过程和面向对象的区别:面向过程:面向对象:总结: 类和对象:定义类:语法: 创建对象:实例演示: 魔法方法:__init __方法:__ del __方法…...
chat聊天系统消息消费时遇到的问题及优化思路(二)
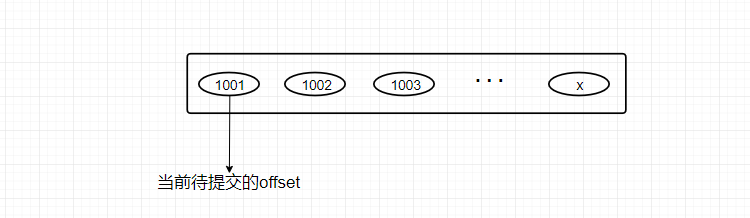
1、前言 考虑下面几个条件下如何提升kafka的消费速度 消息要求严格有序,如chat聊天消息业务处理速度慢,如处理一条数据需要100ms分片不合理,如有的分区很闲,有的分区消息数量积压 2、解决方案 1、顺序问题 关于消息消费时存在…...

js正则中的match()
在前端开发中,正则表达式是一大利器。所以我们这次就来讨论下match()方法。 match本身是JavaScript语言中字符串对象的一个方法,该方法的签名是 match([string] | [RegExp]) 它的参数既可以是一个字符串,也可以是一个正则表达式。该方法绝…...
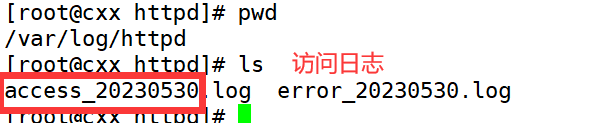
Apache 配置和应用
目录 构建虚拟 Web 主机 Options指令解释 Options指令常用选项 AllowOverride指令解释: 地址限制策略: httpd服务支持的虚拟主机类型包括以下三种: 基于域名的虚拟主机 1.为虚拟主机提供域名解析 2.为虚拟主机准备网页文档 3.添加虚拟…...

实现PyTorch/ONNX自定义节点操作的TensorRT部署
参考一 下面是基本步骤: 加载训练好的bev transformer网络权重参数: import torch from model import Modelmodel Model() model.load_state_dict(torch.load("path/to/weights"))定义新的自定义操作: import torch from torc…...

Shamir 秘密共享、GMW和BGW方案
一、Shamir秘密共享 Shamir秘密共享方案是一种将秘密拆分成多份并分配给多个参与者保存,只有在满足特定条件下才能恢复原始秘密的密码学方案。它具有良好的容错性、加法同态性和无条件安全性等特点。 具体地,Shamir秘密共享方案可以概括为以下步骤&…...

Day56【动态规划】583.两个字符串的删除操作、72.编辑距离
583.两个字符串的删除操作 力扣题目链接/文章讲解 视频讲解 1、确定 dp 数组下标及值含义 dp[i][j]:以下标 i 为结尾的字符串 word1,和以下标 j 为结尾的字符串 word2,想要达到相等,所需要删除元素的最少次数为 dp[i][j] 2、…...

Arnold图像置乱的MATLAB实现
这件事情的起因是这样的,我需要研究一下各种图像置乱的算法。然后在知乎上找到了一篇关于Arnold变化的文章,但是呢,这个人实际上是卖资料,代做大作业的。详细的代码根部不给你,则给我气坏了,必须要手动实现…...
ASP.NET Core
1. 入口文件 一个应用程序总有一个入口文件,是应用启动代码开始执行的地方,这里往往也会涉及到应用的各种配置。当我们接触到一个新框架的时候,可以从入口文件入手,了解入口文件,能够帮助我们更好地理解应用的相关配置…...
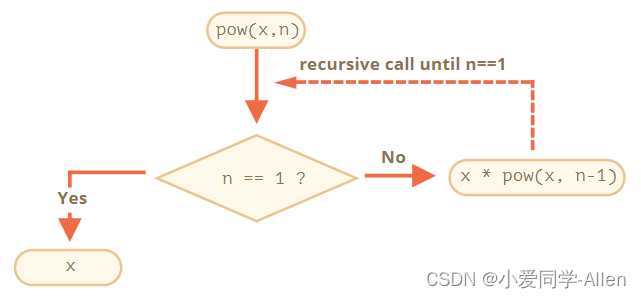
javascript基础二十二:举例说明你对尾递归的理解,有哪些应用场景
一、递归 递归(英语:Recursion) 在数学与计算机科学中,是指在函数的定义中使用函数自身的方法 在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数 其核心思想是把一个大型…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
