【单目标优化算法】孔雀优化算法(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
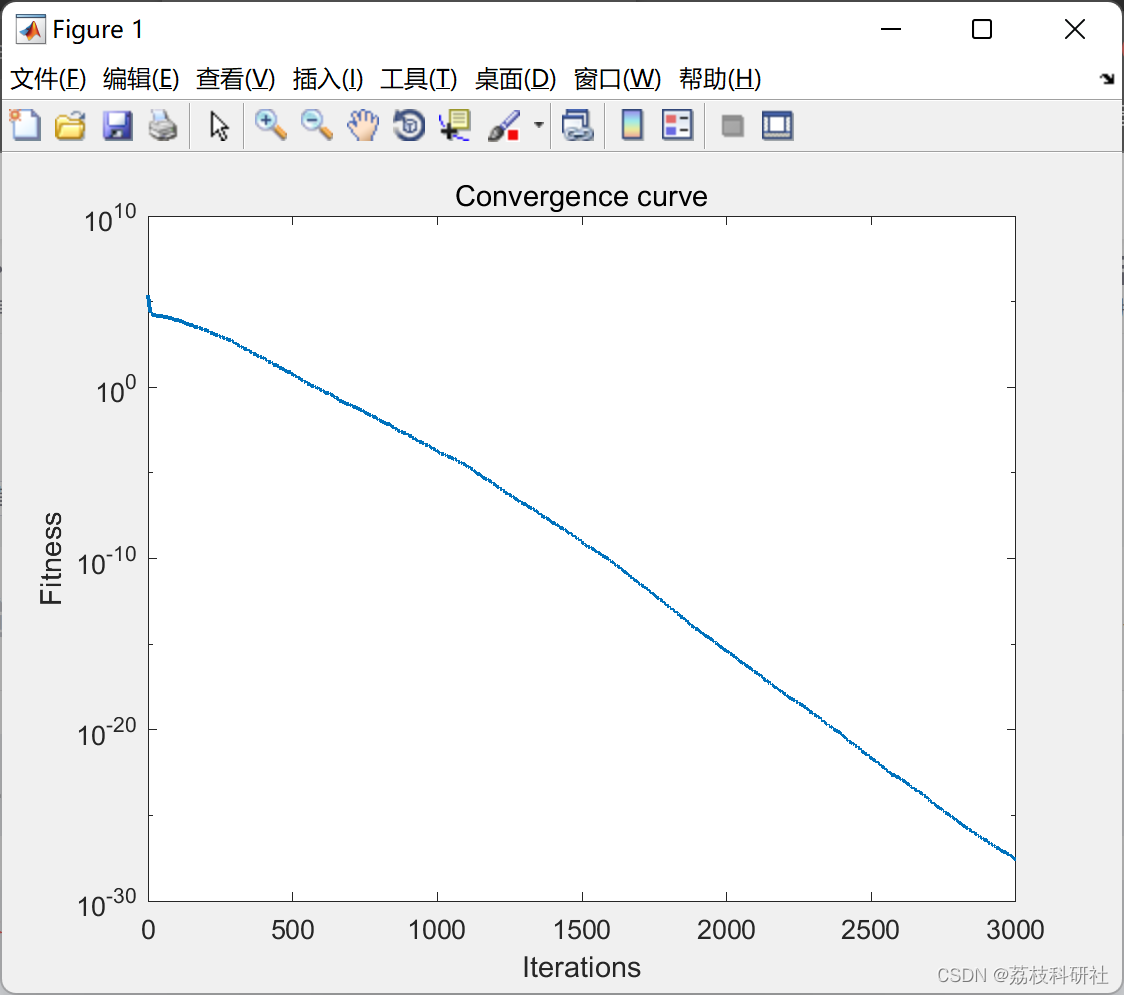
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码及详细文章
💥1 概述

- 受孔雀群智能行为的启发,POA的设计包括有效和高效的探索性和剥削性搜索算子,以在全球探索和局部开发之间提供适当的权衡,以避免局部最优,例如孔雀独特的旋转舞蹈操作,孔雀和孔雀幼崽在不同搜索阶段的自适应搜索行为,以及不同搜索阶段的相互作用 孔雀;
- 代表当前最优解的五只孔雀也会通过旋转跳动机制在附近的搜索空间中搜索,而不是静止不动。孔雀独特的旋转跳舞机制包含两种不同的旋转模式,即原位旋转和围绕食物源盘旋。首先采用当前最优解仍会进行就近搜索的机制,这在以前的算法中从未考虑过,有利于跳出局部最优;
- 孔雀幼崽和孔雀幼崽在整个搜索过程中都倾向于采用适应性搜索和接近机制,动态调整其不同阶段的行为,从而实现局部开发与全球探索之间的适当平衡。
📚2 运行结果
部分代码:
% Peafowl Optimization Algorithm (POA)
function [BestSolution, ConvergenceCurve, Dim]=POA(NumAgents, MaxIterations, BenchmarkFunFlag)
% --------------------------Return Parameters--------------------------
% BestSolution: The best solution
% ConvergenceCurve: Convergence curve
% Dim: The dimensionality of prloblem
% --------------------------Input Parameters---------------------------
% NumAgents: The number of search individuals
% MaxIterations: The number of maximum iterations
% BenchmarkFunFlag: Objective function (1-23)
% ---------------------------------------------------------------------
ConvergenceCurve=zeros(1,MaxIterations);
NumPeacock=5; % the number of leader (Peacock)
NumPeahen=round((NumAgents-NumPeacock)*0.3); % the number of peahen
NumPeacockCub=NumAgents-NumPeacock-NumPeahen; % the number of peacock cub
[LowerBound, UpperBound, Dim]=BenchmarkFunctionRange(BenchmarkFunFlag);
LowerBound=LowerBound*ones(1,Dim);
UpperBound=UpperBound*ones(1,Dim);
SearchRadius0=(UpperBound-LowerBound)*0.2; % initial dance radius of peacock
% initialization
empty_peacock.Position=[];
empty_peacock.Fitness=[];
PeacockPopulation0=repmat(empty_peacock,[NumAgents,1]);
Peahen=repmat(empty_peacock,[NumPeahen,1]);
PeacockCub=repmat(empty_peacock,[NumPeacockCub,1]);
for k=1:NumAgents
PeacockPopulation0(k).Position=LowerBound+(UpperBound-LowerBound).*rand(1,Dim);
PeacockPopulation0(k).Fitness=BenchmarkFunction(PeacockPopulation0(k).Position, BenchmarkFunFlag, Dim);
end
PeacockPopulation=PeacockPopulation0;
[~,index]=sort([PeacockPopulation.Fitness]);
PeacockPopulation=PeacockPopulation(index);
ConvergenceCurve(1)=PeacockPopulation(1).Fitness;
% main loop
for it=2:MaxIterations
SearchRadius=SearchRadius0-(SearchRadius0-0)*(it/MaxIterations)^0.01;
alpha=0.9-(0.9-0.4)*(it/MaxIterations)^2;
delta=0.1+(1-0.1)*(it/MaxIterations)^0.5;
step=0.1+(1-0.1)*(it/MaxIterations);
Peacock=PeacockPopulation(1:NumPeacock);
if rand<1
X_random=2*rand(1,Dim)-1;
Peacock(1).Position=Peacock(1).Position+1*SearchRadius.*X_random/(eps+norm(X_random));
end
if rand<0.9
X_random=2*rand(1,Dim)-1;
Peacock(2).Position=Peacock(2).Position+1.5*SearchRadius.*X_random/(eps+norm(X_random));
end
if rand<0.8
X_random=2*rand(1,Dim)-1;
Peacock(3).Position=Peacock(3).Position+2*SearchRadius.*X_random/(eps+norm(X_random));
end
if rand<0.6
X_random=2*rand(1,Dim)-1;
Peacock(4).Position=Peacock(4).Position+3*SearchRadius.*X_random/(eps+norm(X_random));
end
if rand<0.3
X_random=2*rand(1,Dim)-1;
Peacock(5).Position=Peacock(5).Position+5*SearchRadius.*X_random/(eps+norm(X_random));
end
for k=1:NumPeacock
flag4ub=Peacock(k).Position>UpperBound;
flag4lb=Peacock(k).Position<LowerBound;
Peacock(k).Position=~(flag4ub+flag4lb).*Peacock(k).Position+flag4ub.*UpperBound+flag4lb.*LowerBound;
Peacock(k).Fitness=BenchmarkFunction(Peacock(k).Position, BenchmarkFunFlag, Dim);
if Peacock(k).Fitness < PeacockPopulation(k).Fitness
PeacockPopulation(k)=Peacock(k);
end
end
for k=1:NumPeahen
r1=rand();
if r1 <= 1 && r1 >=0.6
Peahen(k).Position=PeacockPopulation(NumPeacock+k).Position+3*step*(PeacockPopulation(1).Position-PeacockPopulation(NumPeacock+k).Position);
end
if r1 < 0.6 && r1 >=0.4
Peahen(k).Position=PeacockPopulation(NumPeacock+k).Position+3*step*(PeacockPopulation(2).Position-PeacockPopulation(NumPeacock+k).Position);
end
if r1 < 0.4 && r1 >=0.2
Peahen(k).Position=PeacockPopulation(NumPeacock+k).Position+3*step*(PeacockPopulation(3).Position-PeacockPopulation(NumPeacock+k).Position);
end
if r1 < 0.2 && r1 >=0.1
Peahen(k).Position=PeacockPopulation(NumPeacock+k).Position+3*step*(PeacockPopulation(4).Position-PeacockPopulation(NumPeacock+k).Position);
end
if r1 < 0.1 && r1 >=0
Peahen(k).Position=PeacockPopulation(NumPeacock+k).Position+3*step*(PeacockPopulation(5).Position-PeacockPopulation(NumPeacock+k).Position);
end
flag4ub=Peahen(k).Position>UpperBound;
flag4lb=Peahen(k).Position<LowerBound;
Peahen(k).Position=~(flag4ub+flag4lb).*Peahen(k).Position+flag4ub.*UpperBound+flag4lb.*LowerBound;
Peahen(k).Fitness=BenchmarkFunction(Peahen(k).Position, BenchmarkFunFlag, Dim);
if Peahen(k).Fitness < PeacockPopulation(NumPeacock+k).Fitness
PeacockPopulation(NumPeacock+k)=Peahen(k);
end
end
for k=1:NumPeacockCub
PeacockCub(k)=PeacockPopulation(NumPeacock+NumPeahen+k);
r2=rand;
if r2>0.8 && r2<=1
SelectedPeacock=PeacockPopulation(1);
elseif r2>0.6 && r2<=0.8
SelectedPeacock=PeacockPopulation(2);
elseif r2>0.4 && r2<=0.6
SelectedPeacock=PeacockPopulation(3);
elseif r2>0.2 && r2<=0.4
SelectedPeacock=PeacockPopulation(4);
else
SelectedPeacock=PeacockPopulation(5);
end
PeacockCub(k).Position=PeacockCub(k).Position+alpha*Levy(Dim).*( PeacockPopulation(1).Position - PeacockCub(k).Position )+delta*( SelectedPeacock.Position - PeacockCub(k).Position );
flag4ub=PeacockCub(k).Position>UpperBound;
flag4lb=PeacockCub(k).Position<LowerBound;
PeacockCub(k).Position=~(flag4ub+flag4lb).*PeacockCub(k,:).Position+flag4ub.*UpperBound+flag4lb.*LowerBound;
PeacockCub(k).Fitness=BenchmarkFunction(PeacockCub(k).Position, BenchmarkFunFlag, Dim);
if PeacockCub(k).Fitness < PeacockPopulation(NumPeacock+NumPeahen+k).Fitness
PeacockPopulation(NumPeacock+NumPeahen+k)=PeacockCub(k,:);
end
end
Peacock=PeacockPopulation(1:NumPeacock);
Xrandom=2*rand(1,Dim)-1;
Direction1=Peacock(1,:).Position-Peacock(2,:).Position;
Direction2=Xrandom-(Xrandom*Direction1')/(Direction1*Direction1'+eps)*Direction1;
Direction2=Direction2/norm(Direction2+eps)*norm(Direction1);
Peacock(2,:).Position=Peacock(2,:).Position+step*Direction1+rand*Direction2;
Xrandom=2*rand(1,Dim)-1;
Direction1=Peacock(1,:).Position-Peacock(3,:).Position;
Direction2=Xrandom-(Xrandom*Direction1')/(Direction1*Direction1'+eps)*Direction1;
Direction2=Direction2/norm(Direction2+eps)*norm(Direction1);
Peacock(3,:).Position=Peacock(3,:).Position+step*Direction1+rand*Direction2;
Xrandom=2*rand(1,Dim)-1;
Direction1=Peacock(1,:).Position-Peacock(4,:).Position;
Direction2=Xrandom-(Xrandom*Direction1')/(Direction1*Direction1'+eps)*Direction1;
Direction2=Direction2/norm(Direction2+eps)*norm(Direction1);
Peacock(4,:).Position=Peacock(4,:).Position+step*Direction1+rand*Direction2;
Xrandom=2*rand(1,Dim)-1;
Direction1=Peacock(1,:).Position-Peacock(5,:).Position;
Direction2=Xrandom-(Xrandom*Direction1')/(Direction1*Direction1'+eps)*Direction1;
Direction2=Direction2/norm(Direction2+eps)*norm(Direction1);
Peacock(5,:).Position=Peacock(5,:).Position+step*Direction1+rand*Direction2;
for k=1:NumPeacock
flag4ub=Peacock(k).Position>UpperBound;
flag4lb=Peacock(k).Position<LowerBound;
Peacock(k).Position=~(flag4ub+flag4lb).*Peacock(k).Position+flag4ub.*UpperBound+flag4lb.*LowerBound;
Peacock(k).Fitness=BenchmarkFunction(Peacock(k).Position, BenchmarkFunFlag, Dim);
if Peacock(k).Fitness < PeacockPopulation(k).Fitness
PeacockPopulation(k)=Peacock(k);
end
end
[~,index]=sort([PeacockPopulation.Fitness]);
PeacockPopulation=PeacockPopulation(index);
ConvergenceCurve(1,it)=PeacockPopulation(1).Fitness;
end
BestSolution=PeacockPopulation(1);
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] Jingbo Wang, Bo Yang, Yijun Chen, Kaidi Zeng, Hao Zhang, Hongchun Shu, Yingtong Chen,
Novel phasianidae inspired peafowl (Pavo muticus/cristatus) optimization algorithm: Design, evaluation, and SOFC models parameter estimation,
Sustainable Energy Technologies and Assessments
https://doi.org/10.1016/j.seta.2021.101825
🌈4 Matlab代码及详细文章
相关文章:

【单目标优化算法】孔雀优化算法(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

chatgpt赋能python:Python同一行多个语句:如何提高你的编程效率?
Python同一行多个语句:如何提高你的编程效率? Python是一种优雅的编程语言,拥有简洁易懂的语法,可以帮助你快速编写可以在各种领域使用的高级代码。其中,Python同一行多个语句,是一种可以大大提高编程效率…...
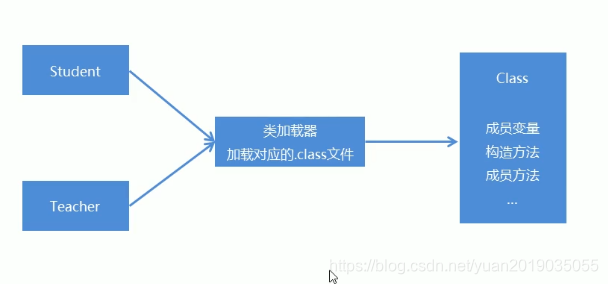
Java反射概述
2 反射 2.1 反射概述 Java反射机制:是指在运行时去获取一个类的变量和方法信息。然后通过获取到的信息来创建对象,调用方法的一种机制。由于这种动态性,可以极大的增强程序的灵活性,程序不用在编译期就完成确定,在运行期仍然可以扩展2.2 反射获取Class类的对象 我们要想通过反…...
)
《网络是怎样连接的》(一)
第一章web浏览器 简介 首先输入网址URL,浏览器进行解析,将我们需要哪些数据告诉服务器。浏览器向服务器发送消息,必须告诉操作系统的接收方的IP地址,所以浏览器先查出web服务器的IP地址,向DNS服务器查询域名对应的IP…...

Flink on yarn任务日志怎么看
1、jobmanager日志 在yarn上可以直接看 2、taskmanager日志 在flink的webui中可以看,但是flink任务失败后,webui就不存在了,那怎么看? 这是jobmanager的地址 hadoop02:19888/jobhistory/logs/hadoop02:45454/container_e03_16844…...
二次元的登录界面
今天还是继续坚持写博客,然后今天给大家带来比较具有二次元风格的登录界面,也只是用html和css来写的,大家可以来看看! 个人名片: 😊作者简介:一名大一在校生,web前端开发专业 &…...
2. 量化多因子数据清洗——去极值、标准化、正交化、中性化
一、去极值 1. MAD MAD(mean absolute deviation)又称为绝对值差中位数法,是一种先需计算所有因子与平均值之间的距离总和来检测离群值的方法. def extreme_MAD(rawdata, n): median rawdata.quantile(0.5) # 找出中位数 new_median (abs(…...

皮卡丘反射型XSS
1.反射型xss(get) 进入反射型xss(get)的关卡,我们可以看到如下页面 先输入合法数据查看情况,例如输入“kobe” 再随便输入一个,比如我舍友的外号“xunlei”,“666”,嘿嘿嘿 F12查看源代码,发现你输入的数…...
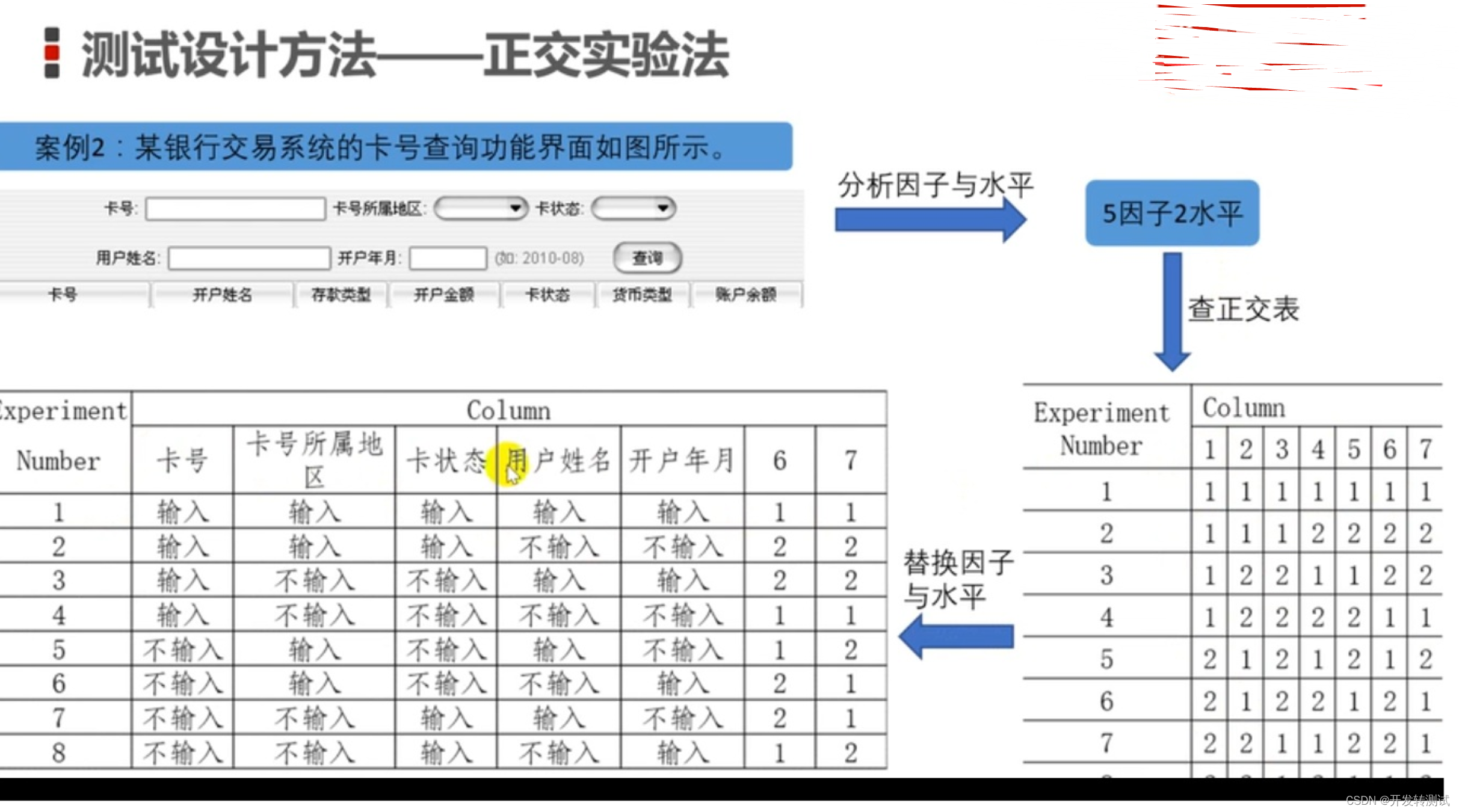
巧计口诀-软件测试的生命周期,黑盒测试设计方法
目录 1。口诀 2。黑盒设计方法适用场合 3。黑盒设计方法详解 3.1。等价类法 3.2。 边界值法 3.3。判定表法 3.4。因果表 3.5。状态迁移图 3.6。场景法 3.7。正交实验法 3.8。错误推断法 1。口诀 又到了找工作的日子,背诵这些基本知识和概念又开始了。我找…...
- Ashmem驱动)
Android系统的Ashmem匿名共享内存系统分析(1)- Ashmem驱动
声明 其实对于Android系统的Ashmem匿名共享内存系统早就有分析的想法,记得2019年6、7月份Mr.Deng离职期间约定一起对其进行研究的,但因为我个人问题没能实施这个计划,留下些许遗憾…文中参考了很多书籍及博客内容,可能涉及的比较…...

Redis 事务详细介绍
事务 注意:Redis单条命令是保证原子性的;但是事务不保证原子性! Redis事务没有隔离级别的概念,所有的命令在事务中,并没有直接被执行,只有发起执行命令时才执行 Redis事务本质:一组命令的集合&…...

2023-5-29第二十九天
consult咨询,查阅,商讨 specialize专门从事,专攻 inspect检查 pattern图案,方式 optimize使最优化 ensemble整体,全体 subscript下标 subscribe签名 sector行业,部门 precedence优先,优…...
【第三方库】PHP实现创建PDF文件和编辑PDF文件
目录 引入Setasign/fpdf、Setasign/fpdi 解决写入中文时乱码问题 1.下载并放置中文语言包(他人封装):https://github.com/DCgithub21/cd_FPDF 2.编写并运行生成字体文件的程序文件(addFont.php) 中文字体举例&…...

线程的回收及内存演示
ps -elf|grep mthread 查看进程和线程 top -p 6513 查看内存 一、线程的回收 使用pthread_join 函数: #include <pthread.h> int pthread_join(pthread_t thread, void **retval); 注意:pthread_join 是阻塞函数,如果回收的线…...

高精度倾角传感器测量原理
高精度倾角传感器测量原理技术参数 1.性能参数 测量范围:0~30 测量精度:0.06 分 辨 率:0.0001 测量方向:X,Y 时间漂移:0.08/月 更新时间:30ms 上电启动时间:0.5s 2.电…...

Android 12 init流程分析
前言 刚开始接触需要了解的概念理解过程遇到了什么问题代码的位置和流程分析如何分析和调试遇到的问题 基本的概念 .rc 文件 这个文件在Android framework 中服务相关代码可以看到。类似surfaceflinger.rc 、mediaserver.rc等等。 在这些rc里面定义了某一个service࿰…...

【Python小技巧】Python操控Chrome浏览器实现网页打开、切换、关闭(送独家Chrome操作打包类源码、Chrome浏览器Cookie在哪里?)
文章目录 前言一、什么时候需要用Python控制浏览器?二、下载Chrome浏览器驱动文件1. 安装Chrome浏览器并查看版本2. 下载浏览器驱动文件3. 解压到python编译器目录(python.exe所在目录) 三、Python控制Chrome浏览器(附源代码&…...

数据在内存中的存储
目录 一、数据类型的介绍 1.C语言基本内置类型 2.类型基本归类 1.整形 2.浮点型 3.构造类型 4.指针类型 二、整形在内存中的存储 三、浮点数在内次中的存储 1.存储形式 2.对M、E的特殊规定 (1)对M的特殊规定 (2)对E的…...

Rust in Action笔记 第三章 复合数据类型
通过#[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZI50wIh1-1685693144796)(null)]),不带感叹号的#[allow]仅为下一行代码提供属性,属性有多种分类,文中出现的allow属性称为诊断属性(Diag…...

算法基础学习笔记——⑬高斯消元\组合计数\容斥原理
✨博主:命运之光 ✨专栏:算法基础学习 目录 ✨高斯消元 ✨组合计数 🍓通过预处理逆元的方式求组合数: 🍓Lucas定理: 🍓分解质因数法求组合数: 前言:算法学习笔记记录日常分享,需…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
