【LeetCode 算法】Minimum Operations to Halve Array Sum 将数组和减半的最少操作次数-Greedy
Minimum Operations to Halve Array Sum 将数组和减半的最少操作次数
问题描述:
给你一个正整数数组 nums 。每一次操作中,你可以从 nums 中选择 任意 一个数并将它减小到 恰好 一半。(注意,在后续操作中你可以对减半过的数继续执行操作)
请你返回将 nums 数组和 至少 减少一半的 最少 操作数。
1 < = n u m s . l e n g t h < = 1 0 5 1 < = n u m s [ i ] < = 1 0 7 1 <= nums.length <= 10^5\\ 1 <= nums[i] <= 10^7 1<=nums.length<=1051<=nums[i]<=107
分析
目标是将数组的和减少到原始数组和的一半,而且是最小的操作数。
一次操作可以选任意的元素减半,而且可以重复选择某个下标的元素。所以几乎不存在限制。
也就是说一定在经过若干次操作后,可以达到目标。
记原始数组和为 s u m sum sum,那么目标就是 h a l f = s u m / 2 half = sum/2 half=sum/2;
但是问题是要求最少的,所以细化一下目标,
- 如果最后一次的操作使得最新的数组和 s ′ = = h a l f s'==half s′==half,说明这是最后一次操作,
- 同样如果 s ′ < h a l f s'<half s′<half,也是说明最后一次操作。
- 如果 s ′ > h a l f s'>half s′>half,说明还需要进行操作。
而且为了使得能够尽快使 s ′ s' s′靠近到目标 h a l f half half,每次一定是选择当前数组中的 m a x max max,进行操作。
暴力
如果是暴力的算法,就是每次选择最大,然后减半,放回去,再找一次最大,循环往复。
每次找数组的最大值的时间复杂度 O ( N ) O(N) O(N),而且要达到目标需要操作N次,整体的时间复杂度为 O ( N 2 ) O(N^2) O(N2).
所以这个暴力的时间复杂度有TLE的风险。
优先队列
所以就需要进行加速,而唯一能选的就是优先队列。
在优先队列中的维护一个最大值或最小值的平均时间复杂度是 O ( l o g N ) O(logN) O(logN),所以整体的时间复杂度就会降低到 O ( N l o g N ) O(NlogN) O(NlogN).
同时需要注意的是数据的范围,以及精度。
代码
TLE
public int halveArray(int[] nums) {Double tot = 0.0;int n = nums.length;Double[] arr = new Double[n];for(int i =0;i<n;i++){arr[i] = nums[i]*1.0;tot+= arr[i];}Double half = tot*0.5;int ans =0;for(int i =0;i<n;i++){if(half<=0) break;int id =0;double max = arr[id];for(int j =0;j<n;j++){if(arr[j]>max){max = arr[j];id = j;}}arr[id] *= 0.5;half -= arr[id];ans++;}return ans;}时间复杂度 O ( N 2 ) O(N^2) O(N2)
空间复杂度 O ( 1 ) O(1) O(1)
优先队列
public int halveArray(int[] nums) {PriorityQueue<Double> pq = new PriorityQueue<Double>((a,b)->{return b.compareTo(a);});Double tot = 0.0;for(int num: nums){Double t = num*1.0;tot+=t;pq.offer(t);} Double half = tot*0.5;int ans =0;while(half>0&&!pq.isEmpty()){Double t = pq.poll();t *=0.5;half -= t;ans++;pq.offer(t);}return ans;}
时间复杂度 O ( N l o g N ) O(NlogN) O(NlogN)
空间复杂度 O ( N ) O(N) O(N)
Tag
Array
Greedy
Heap
相关文章:

【LeetCode 算法】Minimum Operations to Halve Array Sum 将数组和减半的最少操作次数-Greedy
文章目录 Minimum Operations to Halve Array Sum 将数组和减半的最少操作次数问题描述:分析代码TLE优先队列 Tag Minimum Operations to Halve Array Sum 将数组和减半的最少操作次数 问题描述: 给你一个正整数数组 nums 。每一次操作中,你…...

Doc as Code (3):业内人士的观点
作者 | Anne-Sophie Lardet 在技术传播国际会议十周年之际,Fluid Topics 的认证技术传播者和功能顾问 Gaspard上台探讨了“docOps 作为实现Doc as Code的中间结构”的概念。在他的演讲中,观众提出了几个问题,我们想分享Gaspard的见解&#x…...
【Kafka】消息队列Kafka基础
目录 消息队列简介消息队列的应用场景异步处理系统解耦流量削峰日志处理 消息队列的两种模式点对点模式发布订阅模式 Kafka简介及应用场景Kafka比较其他MQ的优势Kafka目录结构搭建Kafka集群编写Kafka一键启动/关闭脚本 Kafka基础操作创建topic生产消息到Kafka从Kafka消费消息使…...
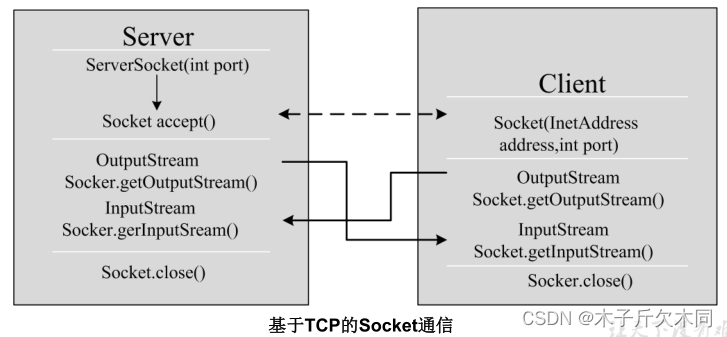
Java的第十五篇文章——网络编程(后期再学一遍)
目录 学习目的 1. 对象的序列化 1.1 ObjectOutputStream 对象的序列化 1.2 ObjectInputStream 对象的反序列化 2. 软件结构 2.1 网络通信协议 2.1.1 TCP/IP协议参考模型 2.1.2 TCP与UDP协议 2.2 网络编程三要素 2.3 端口号 3. InetAddress类 4. Socket 5. TCP网络…...

【深度学习】High-Resolution Image Synthesis with Latent Diffusion Models,论文
13 Apr 2022 论文:https://arxiv.org/abs/2112.10752 代码:https://github.com/CompVis/latent-diffusion 文章目录 PS基本概念运作原理 AbstractIntroductionRelated WorkMethodPerceptual Image CompressionLatent Diffusion Models Conditioning Mec…...

前端学习——Vue (Day6)
路由进阶 路由的封装抽离 //main.jsimport Vue from vue import App from ./App.vue import router from ./router/index// 路由的使用步骤 5 2 // 5个基础步骤 // 1. 下载 v3.6.5 // 2. 引入 // 3. 安装注册 Vue.use(Vue插件) // 4. 创建路由对象 // 5. 注入到new Vue中&…...
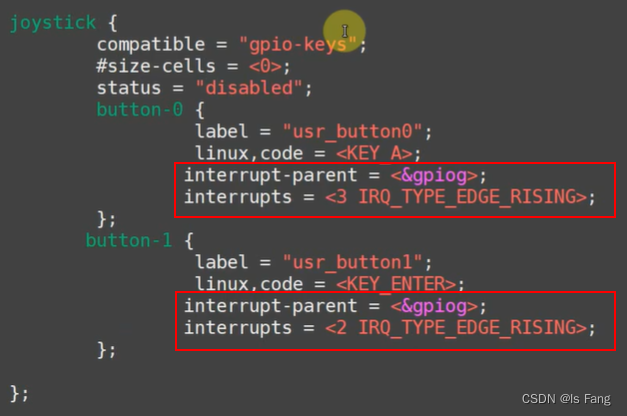
STM32MP157驱动开发——按键驱动(tasklet)
文章目录 “tasklet”机制:内核函数定义 tasklet使能/ 禁止 tasklet调度 tasklet删除 tasklet tasklet软中断方式的按键驱动程序(stm32mp157)tasklet使用方法:button_test.cgpio_key_drv.cMakefile修改设备树文件编译测试 “tasklet”机制: …...
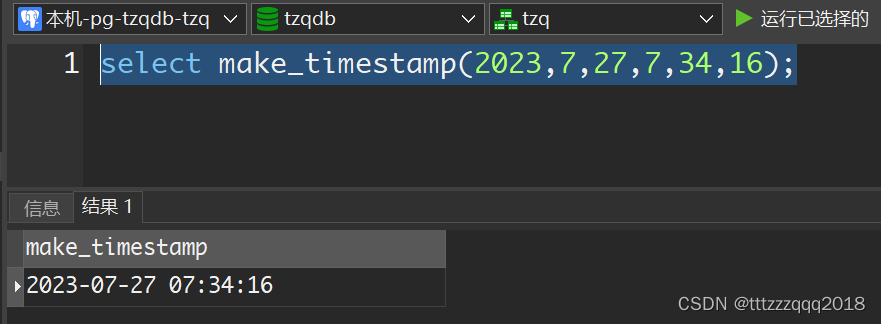
PostgreSQL构建时间
– PostgreSQL构建时间 select make_timestamp(2023,7,27,7,34,16);...

2023-将jar包上传至阿里云maven私有仓库(云效制品仓库)
一、背景介绍 如果要将平时积累的代码工具jar包,上传至云端,方便团队大家一起使用,一般的方式就是上传到Maven中心仓库(但是这种方式步骤多,麻烦,而且上传之后审核时间比较长,还不太容易通过&a…...

嵌入式linux之OLED显示屏SPI驱动实现(SH1106,ssd1306)
周日业余时间太无聊,又不喜欢玩游戏,大家的兴趣爱好都是啥?我觉得敲代码也是一种兴趣爱好。正巧手边有一块儿0.96寸的OLED显示屏,一直在吃灰,何不把玩一把?于是说干就干,最后在我的imax6ul的lin…...
关于element ui 安装失败的问题解决方法、查看是否安装成功及如何引入
Vue2引入 执行npm i element-ui -S报错 原因:npm版本太高 报错信息: 解决办法: 使用命令: npm install --legacy-peer-deps element-ui --save 引入: 在main.js文件中引入 //引入Vue import Vue from vue; //引入…...
Selenium多浏览器处理
Python 版本 #导入依赖 import os from selenium import webdriverdef test_browser():#使用os模块的getenv方法来获取声明环境变量browserbrowser os.getenv("browser").lower()#判断browser的值if browser "headless":driver webdriver.PhantomJS()e…...

浅谈 AI 大模型的崛起与未来展望:马斯克的 xAI 与中国产业发展
文章目录 💬话题📋前言🎯AI 大模型的崛起🎯中国 AI 产业的进展与挑战🎯AI 大模型的未来展望🧩补充 📝最后 💬话题 北京时间 7 月 13 日凌晨,马斯克在 Twiiter 上宣布&am…...
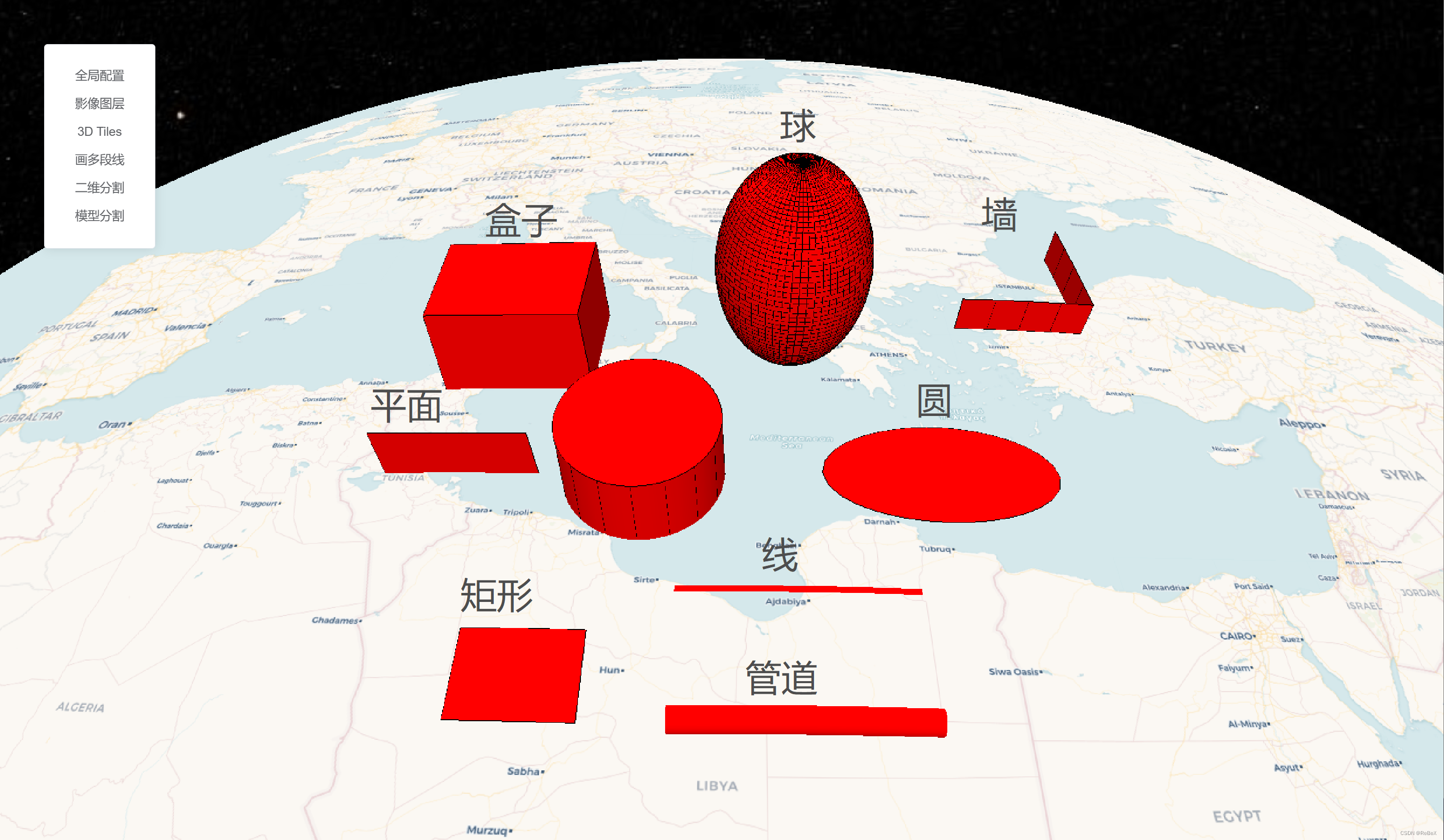
【CesiumJS材质】(1)圆扩散
效果示例 最佳实践: 其他效果: 要素说明: 代码 /** Date: 2023-07-21 15:15:32* LastEditors: ReBeX 420659880qq.com* LastEditTime: 2023-07-27 11:13:17* FilePath: \cesium-tyro-blog\src\utils\Material\EllipsoidFadeMaterialP…...

实战-单例模式和创建生产者相结合
实际中遇到了这样一个问题: The producer group[xxxx] has been created before, specify another instanceName (like producer.setInstanceName) please. 发生的原因是:一个进程内,创建了多个相同topic的producer。 所以问题就转换成了如何…...

[SQL挖掘机] - 窗口函数介绍
介绍: 窗口函数也称为 OLAP 函数。OLAP 是 OnLine AnalyticalProcessing 的简称,意思是对数据库数据进行实时分析处理。窗口函数是一种用于执行聚合计算和排序操作的功能强大的sql函数。它们可以在查询结果集中创建一个窗口(window)…...

原生js实现锚点滚动顶部
简介 使用原生js API实现滚动到指定容器的顶部,API是scrollIntoView 使用 let eldocment.querySelector() 获取dom元素el.scrollIntoView()该元素滚动到其父元素的顶部 高级用法 scrollIntoView(Options)//option可以配置如下 options{behavior:smoot…...

使用mysql接口遇到点问题
game_server加入了dbstorage的代码。dbstorage实现了与mysql的交互:driver_mysql。其中调用了mysql相关的接口。所以game_server需要链接libmysql.lib。 从官网下载了mysql的源码:在用cmake构建mysql工程的时候,遇到了一些问题。 msyql8.0需…...
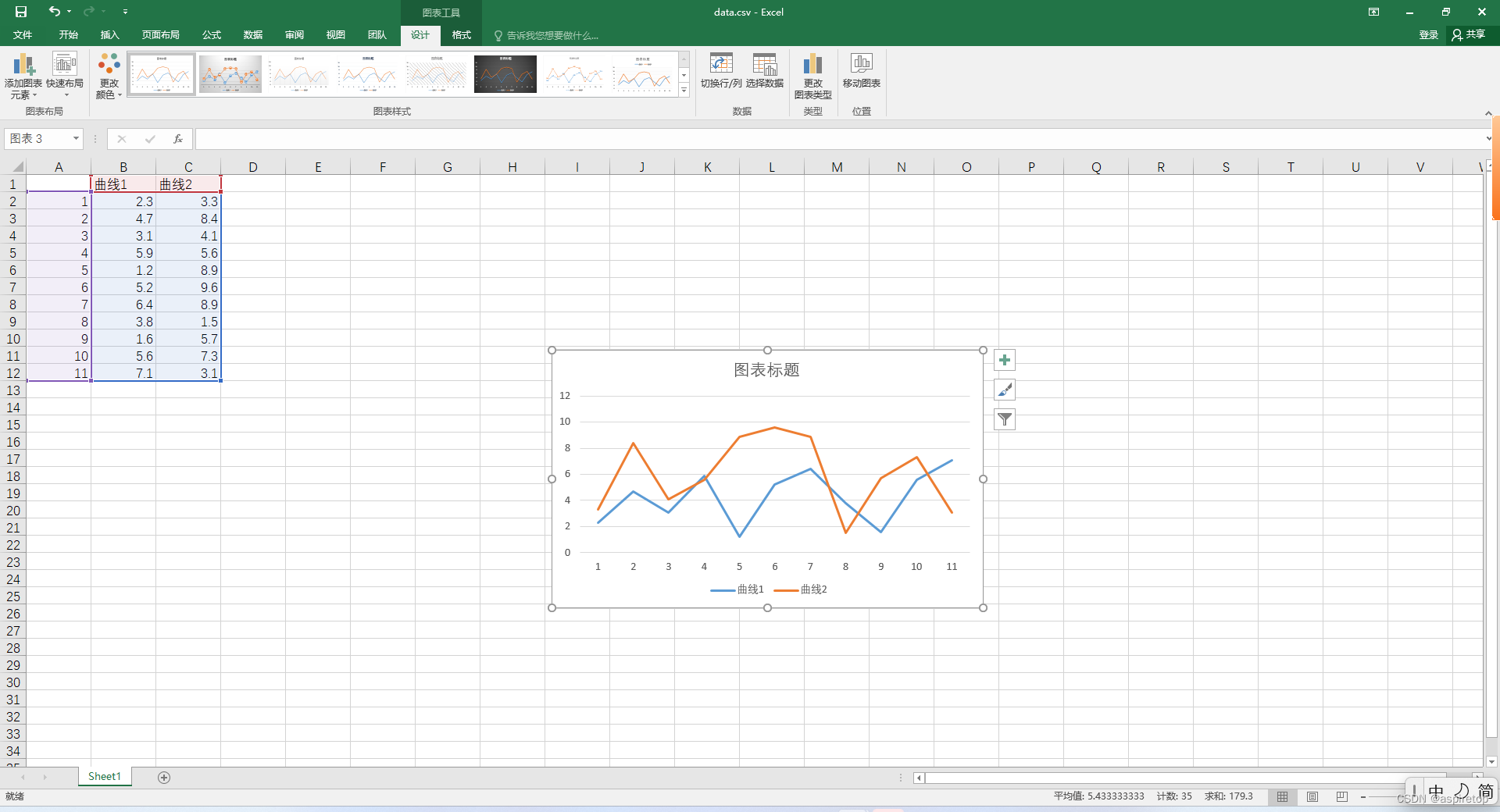
excel绘制折线图或者散点图
一、背景 假如现在通过代码处理了一批数据,想看数据的波动情况,是不是还需要写个pyhon代码,读取文件,绘制曲线,看起来也简单,但是还有更简单的方法,就是直接生成csv文件,csv文件就是…...
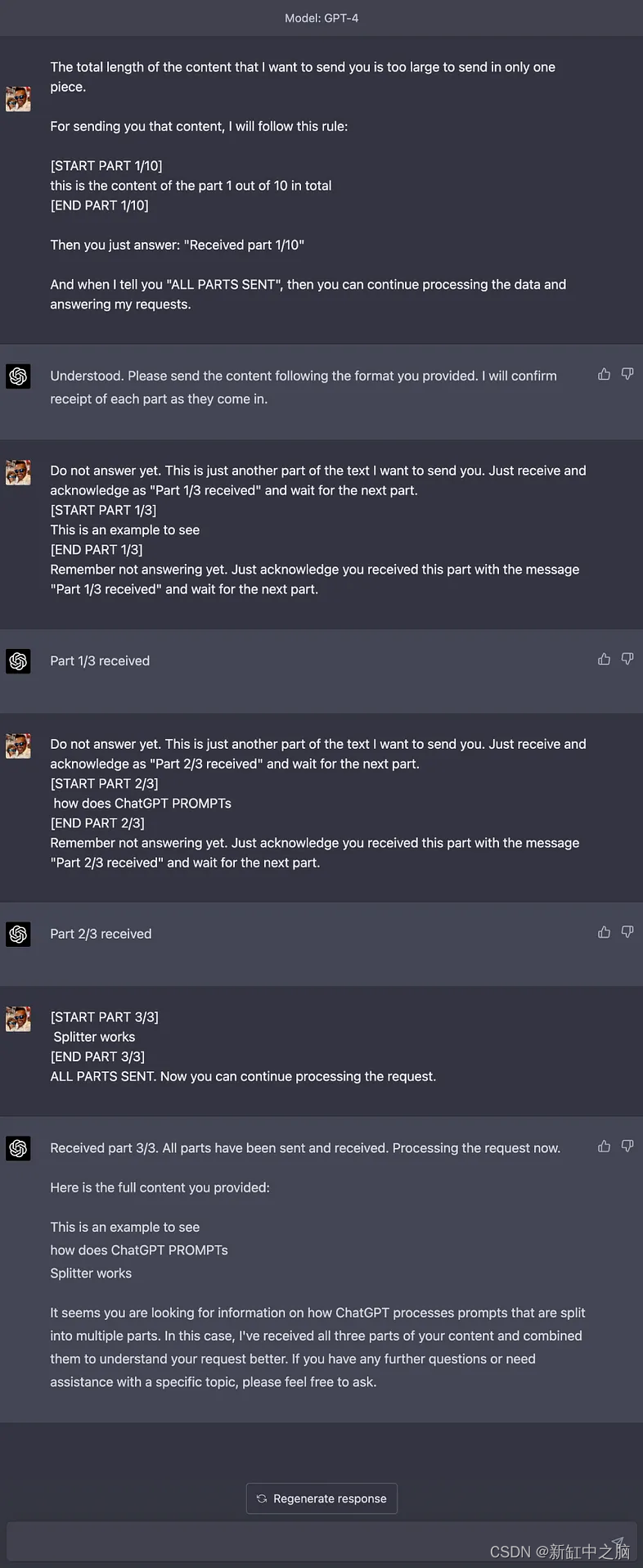
ChatGPT长文本对话输入方法
ChatGPT PROMPTs Splitter 是一个开源工具,旨在帮助你将大量上下文数据分成更小的块发送到 ChatGPT 的提示,并根据如何处理所有块接收到 ChatGPT(或其他具有字符限制的语言模型)的方法。 推荐:用 NSDT设计器 快速搭建可…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
