LeetCode 1237. 找出给定方程的正整数解
原题链接
难度:middle\color{orange}{middle}middle
2023/2/18 每日一题
题目描述
给你一个函数 f(x,y)f(x, y)f(x,y) 和一个目标结果 zzz,函数公式未知,请你计算方程 f(x,y)==zf(x,y) == zf(x,y)==z 所有可能的正整数 数对 xxx 和 yyy。满足条件的结果数对可以按任意顺序返回。
尽管函数的具体式子未知,但它是单调递增函数,也就是说:
- f(x,y)<f(x+1,y)f(x, y) < f(x + 1, y)f(x,y)<f(x+1,y)
- f(x,y)<f(x,y+1)f(x, y) < f(x, y + 1)f(x,y)<f(x,y+1)
函数接口定义如下:
interface CustomFunction {
public:// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.int f(int x, int y);
};
你的解决方案将按如下规则进行评判:
- 判题程序有一个由 CustomFunctionCustomFunctionCustomFunction 的 999 种实现组成的列表,以及一种为特定的 zzz 生成所有有效数对的答案的方法。
- 判题程序接受两个输入:functionidfunction_idfunctionid(决定使用哪种实现测试你的代码)以及目标结果 zzz 。
- 判题程序将会调用你实现的 findSolutionfindSolutionfindSolution 并将你的结果与答案进行比较。
- 如果你的结果与答案相符,那么解决方案将被视作正确答案,即 AcceptedAcceptedAccepted 。
示例 1:
输入:function_id = 1, z = 5
输出:[[1,4],[2,3],[3,2],[4,1]]
解释:function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5
示例 2:
输入:function_id = 2, z = 5
输出:[[1,5],[5,1]]
解释:function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5
提示:
- 1<=functionid<=91 <= function_id <= 91<=functionid<=9
- 1<=z<=1001 <= z <= 1001<=z<=100
- 题目保证 f(x,y)==zf(x, y) == zf(x,y)==z 的解处于 1<=x,y<=10001 <= x, y <= 10001<=x,y<=1000 的范围内。
- 在 1<=x,y<=10001 <= x, y <= 10001<=x,y<=1000 的前提下,题目保证 f(x,y)f(x, y)f(x,y) 是一个 32 位有符号整数。
算法
(暴力枚举) O(n2)O(n^2)O(n2)
-
枚举
x和y,调用接口判断f(x, y)是否等于z。 -
如果等于
z,则加入答案中,如果大于z,则终止掉内层循环。
复杂度分析
-
时间复杂度:最坏情况下,需要判断每一个数对,故时间复杂度为 O(n2)O(n^2)O(n2)。
-
空间复杂度 : 需要存储答案,故空间复杂度也为 O(n2)O(n^2)O(n2)。
C++ 代码
/** // This is the custom function interface.* // You should not implement it, or speculate about its implementation* class CustomFunction {* public:* // Returns f(x, y) for any given positive integers x and y.* // Note that f(x, y) is increasing with respect to both x and y.* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)* int f(int x, int y);* };*/class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> res;for (int x = 1; x <= 1000; x ++) for (int y = 1; y <= 1000; y ++) if (customfunction.f(x, y) == z) {res.push_back({x, y});}return res;}
};
- 双指针
/** // This is the custom function interface.* // You should not implement it, or speculate about its implementation* class CustomFunction {* public:* // Returns f(x, y) for any given positive integers x and y.* // Note that f(x, y) is increasing with respect to both x and y.* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)* int f(int x, int y);* };*/class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> res;int x = 1, y = 1000;while (x <= 1000 && y >= 1) {int t = customfunction.f(x, y);if (t > z) y --;else if (t < z) x ++;else {res.push_back({x, y});x ++, y --;}}return res;}
};
相关文章:

LeetCode 1237. 找出给定方程的正整数解
原题链接 难度:middle\color{orange}{middle}middle 2023/2/18 每日一题 题目描述 给你一个函数 f(x,y)f(x, y)f(x,y) 和一个目标结果 zzz,函数公式未知,请你计算方程 f(x,y)zf(x,y) zf(x,y)z 所有可能的正整数 数对 xxx 和 yyy。满足条件…...
【ArcGIS Pro二次开发】(5):UI管理_自定义控件的位置
新增的自定义控件一般放在默认的【加载项】选项卡下,但是根据需求,我们可能需要将控件放在新的自定义选项卡下,在自定义选项卡添加系统自带的控件,将自定义的按钮等控件放在右键菜单栏里以方便使用,等等。 下面就以一…...

学习OpenGL图形2D/3D编程
环境:WindowsVisual Studio 2019最流行的几个库:GLUT,SDL,SFML和GLFWGLFWGLAD库查看显卡OPENGL支持情况VS2019glfwgladopenGL3.3顶点着色器片段着色器VAO-VBO-(EBO)->渲染VAO-VBO-EBO->texture纹理矩阵matrix对图形transfor…...

2023美赛思路 | A题时间序列预测任务的模型选择总结
2023美赛思路 | A题时间序列预测任务的模型选择总结 目录 2023美赛思路 | A题时间序列预测任务的模型选择总结基本介绍数据描述任务介绍时序模型基本介绍 这道题分析植被就行,主要涉及不同植被间的相互作用,有竞争有相互促进,我查了下“植物科学数据中心”和“中国迁地保护植…...
PHP教材管理系统设计(源代码+毕业论文)
【P003】PHP教材管理系统设计(源代码论文) 设计方案 本系统采用B/S结构,所有的程序及数据都放在服务器上,终端在取得相应的权限后使用Web页面浏览,录入,修改等功能。在语言方面使用PHP语言,在…...
nps内网穿透工具
一、准备一台有公网ip的服务器 https://github.com/ehang-io/nps/releases 在这个地址下载服务端的安装包,centos的下载这个 上传到服务器上。 二、然后解压,安装,启动 [rootadministrator ~]# tar xzvf linux_amd64_server.tar.gz [roo…...

webpack打包时的热模块替代配置以及source-map
1.HMR 在devServer当中添加hot:true 热模块化功能 含义:当其中有一个文件发生变化的时候,那么就会被重新打包一次,极大的提高了构建速度 A.样式文件:可以使用HMR功能,因为在style-loader当中实现了 B.js文件:默认不能使用HMR功能…...
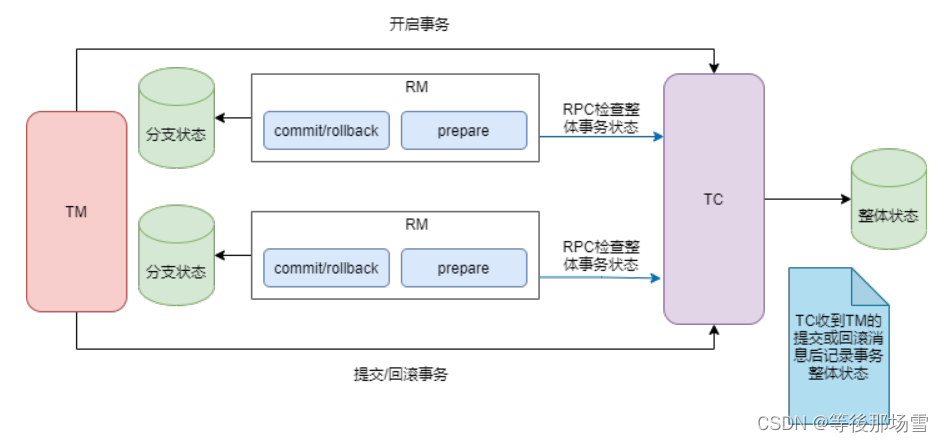
Seata架构篇 - TCC模式
TCC 模式 概述 TCC 是分布式事务中的两阶段提交协议,它的全称为 Try-Confirm-Cancel,即资源预留(Try)、确认操作(Confirm)、取消操作(Cancel)。Try:对业务资源的检查并…...
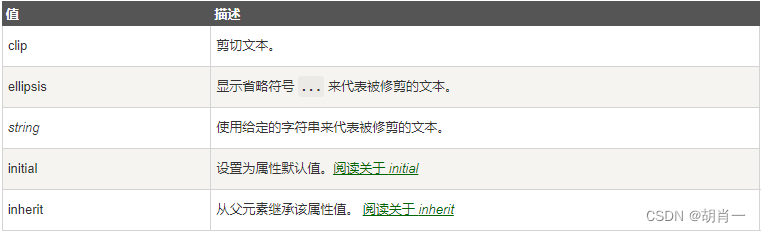
前端最全面试题整理
前端基础 一、 HTTP/HTML/浏览器 1、说一下 http 和 https https 的 SSL 加密是在传输层实现的。 (1) http 和 https 的基本概念 http: 超文本传输协议,是互联网上应用最为广泛的一种网络协议,是一个客户端和服务器端请求和应答的标准(T…...
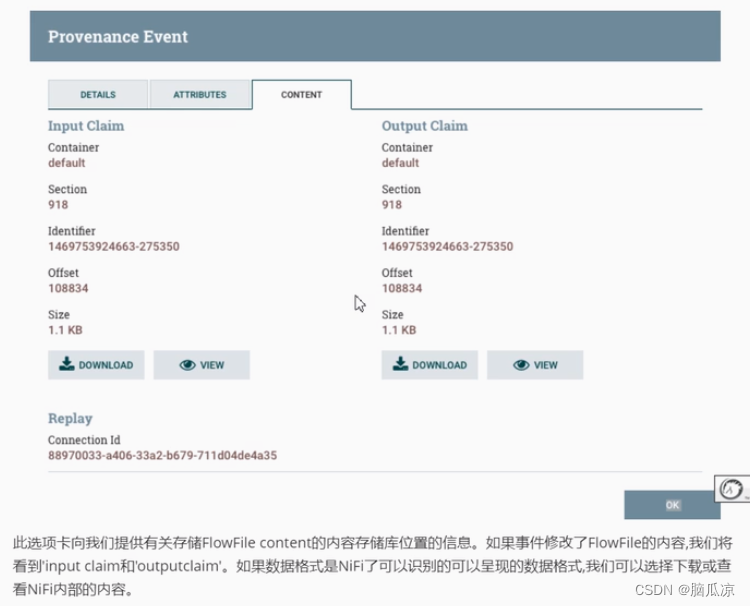
大数据之-Nifi-监控nifi数据流信息_监控数据来源_bub轻松复现---大数据之Nifi工作笔记0011
通过数据流功能可以轻松复现,数据的流向在某个时间点数据是怎么流动的,出现了什么问题,太强大了.. 真的是,可以看到通过右键,处理器,打开view data province就可以看到, 上面是处理器处理数据的详细信息 点击左侧的详情图标可以查看详情信息,details是这个事件处理的内容详情,…...

CUDA编程接口
编程接口 文章目录编程接口3.1利用NVCC编译3.1.1编译流程3.1.1.1 离线编译3.1.1.2 即时编译3.1.2 Binary 兼容性注意:仅桌面支持二进制兼容性。 Tegra 不支持它。 此外,不支持桌面和 Tegra 之间的二进制兼容性。3.1.3 PTX 兼容性3.1.4 应用程序兼容性3.1…...

惠普打印机使用
https://support.hp.com/cn-zh/product/hp-officejet-4500-all-in-one-printer-series-g510/3919445/document/c02076511HP 打印机 - 无法打印校准页本文适用于 HP 喷墨打印机。安装新墨盒后,打印机无法按预期打印校准页。步骤 1:确保打印机可以开始打印…...

Ubuntu升级cmake
目录 1、下载cmake安装包 2、开始安装 3、查看cmake版本 参考链接: https://blog.csdn.net/qq_27350133/article/details/121994229 1、下载cmake安装包 cmake安装包下载:download | cmake 我们根据自身需求下载所需版本的cmake安装包,这…...

CCNP350-401学习笔记(101-150题)
101、Refer to the exhibit SwitchC connects HR and Sales to the Core switch However, business needs require that no traffic from the Finance VLAN traverse this switch. Which command meets this requirement? A. SwitchC(config)#vtp pruning B. SwitchC(config)#…...

分享112个HTML娱乐休闲模板,总有一款适合您
分享112个HTML娱乐休闲模板,总有一款适合您 112个HTML娱乐休闲模板下载链接:https://pan.baidu.com/s/15uBy1SVSckPPMM55fiudeQ?pwdkqfz 提取码:kqfz Python采集代码下载链接:采集代码.zip - 蓝奏云 Bootstrap视频网站模板 …...
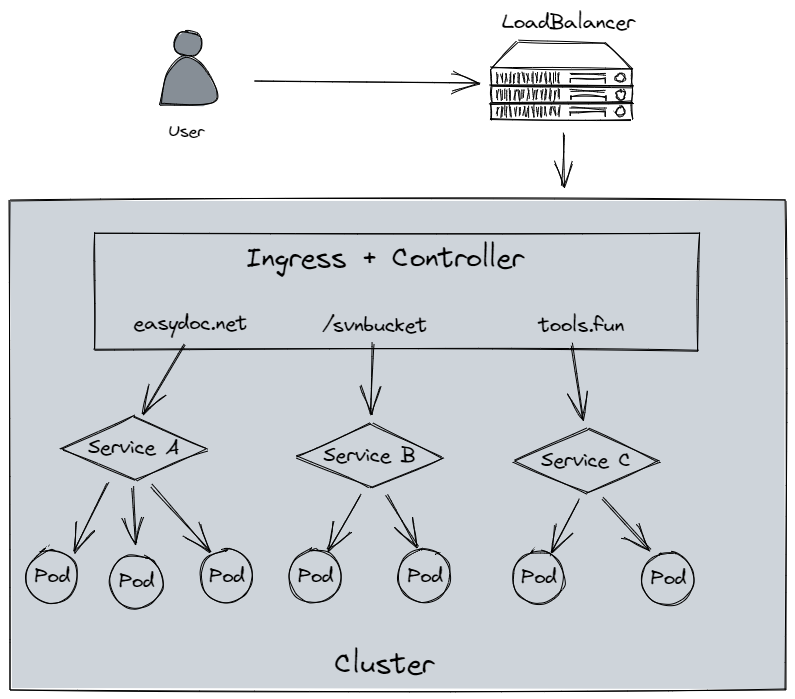
k8s快速入门
文章目录一、Kubernetes(K8S)简介1、概念1.1 Kubernetes (K8S) 是什么1.2 核心特性1.3 部署方案2、Kubernetes 集群架构2.1 架构2.2 重要概念 Pod2.3 Kubernetes 组件二、Kubernetes集群安装1、安装方式介绍2、minikubute安装3、裸机搭建(Bar…...

NG ZORRO知识点总结
NG ZORRO的常用属性,包括但不限于,结合代码 <button nz-button [nzType]"primary" [nzSize]"large" [nzLoading]"loading" [nzDisabled]"disabled" (click)"onClick()">点击我</button>nz-button是一个按钮组件…...

go中的值方法和指针方法
go中的值方法和指针方法1前言2 不同类型的对象调用不同类型的方法2.1 值对象可以调用值方法和指针方法3 指针对象可以调用值方法和指针方法4 !注意:结构体对象实现接口方法1前言 golang中在给结构体对象添加方法时,接收者参数类型可以有两种…...

OKR常见挑战以及应对方法探讨
背景 OKR是大家经常听到的一个词,也有不少团队说自己实行过,但每个实行过的团队都遇到过挑战。很多团队都感觉OKR有些空,很难落地,普通团队成员更是时常感觉无所适从,感觉就像看电影。2022年我们在更大的范围落地了OK…...
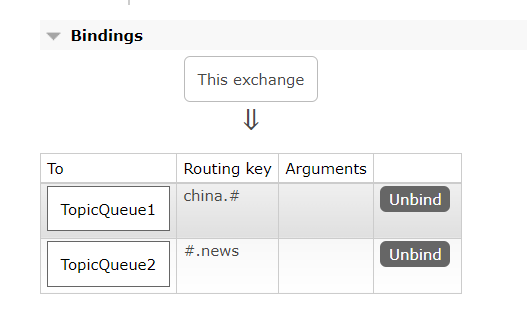
SpringAMQP消息队列(SpringBoot集成RabbitMQ)
一、初始配置1、导入maven坐标<!--rabbitmq--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId></dependency>2、yml配置spring:rabbitmq:host: 你的rabbitmq的ipport: …...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...

接口 RESTful 中的超媒体:REST 架构的灵魂驱动
在 RESTful 架构中,** 超媒体(Hypermedia)** 是一个核心概念,它体现了 REST 的 “表述性状态转移(Representational State Transfer)” 的本质,也是区分 “真 RESTful API” 与 “伪 RESTful AP…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...
