【(C语言)数据结构奋斗100天】二叉树(上)
【(C语言)数据结构奋斗100天】二叉树(上)
🏠个人主页:泡泡牛奶
🌵系列专栏:数据结构奋斗100天
本期所介绍的是二叉树,那么什么是二叉树呢?在知道答案之前,请大家思考一下下列问题:
- 什么是二叉树的根节点?
- 什么是二叉树的左子树和右子树?
- 什么是二叉树的父节点和子节点?
- 二叉树的遍历有哪些方法?
让我们带着这些问题,开始今天的学习吧( •̀ ω •́ )✧
一、树和二叉树
1. 什么是树?
树是一种非线性的数据结构,是(n>=0)个节点的有限集合。当n=0时,称为空树。在任意一颗非空树中,我们可以看到节点的排列就像一颗倒着的树,根朝上,叶子朝下
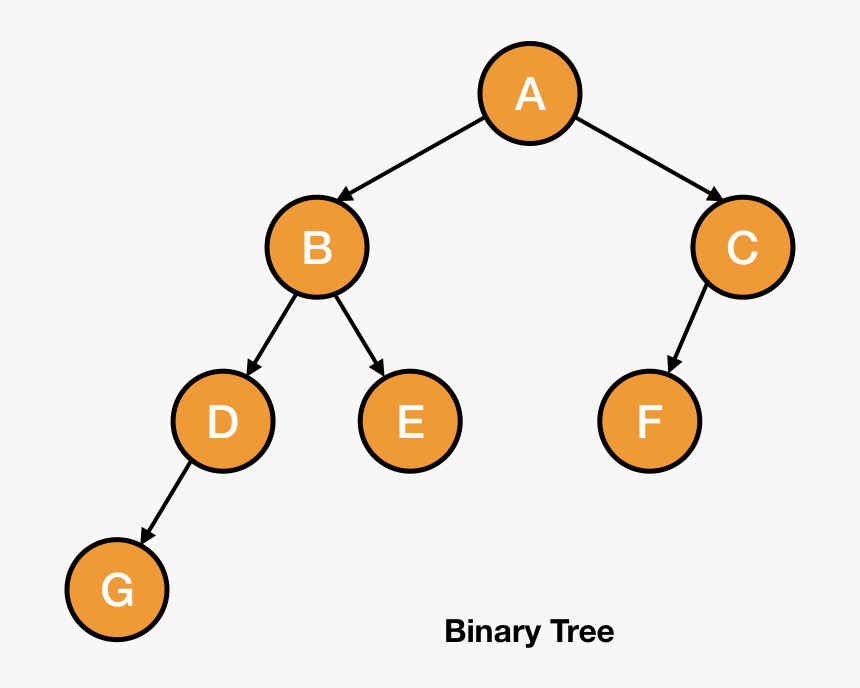
在现实生活中有哪些像上面根朝上,叶子朝下的树型结构呢🤔?

例如一个家族里组成的 “家谱” ,就是一颗树。
再例如一个阶级关系就是一颗 “树”。
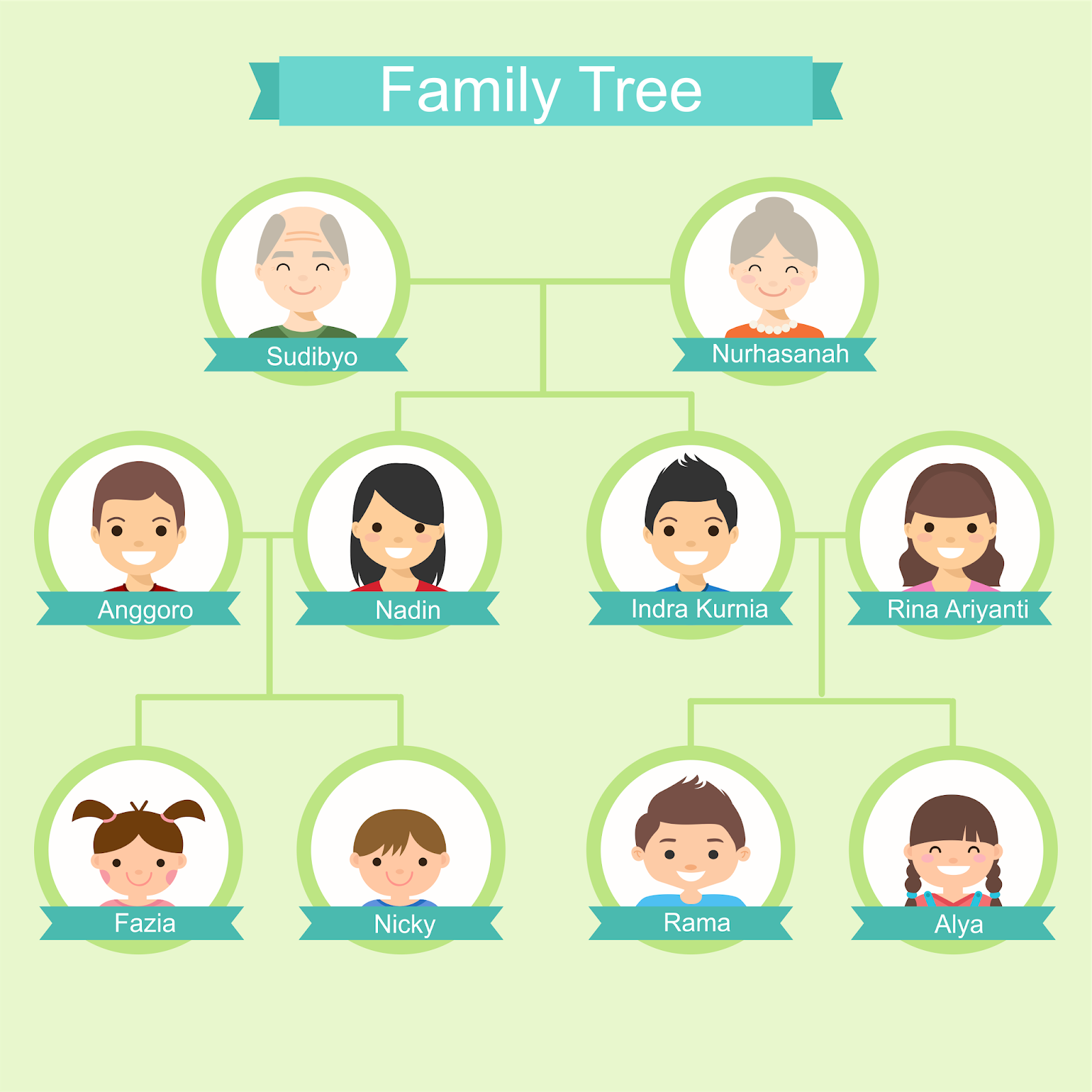
除开人与人的关系,还有很多抽象的东西也可以成为一颗 “树”,如一本书的目录,如操作系统的文件系统。
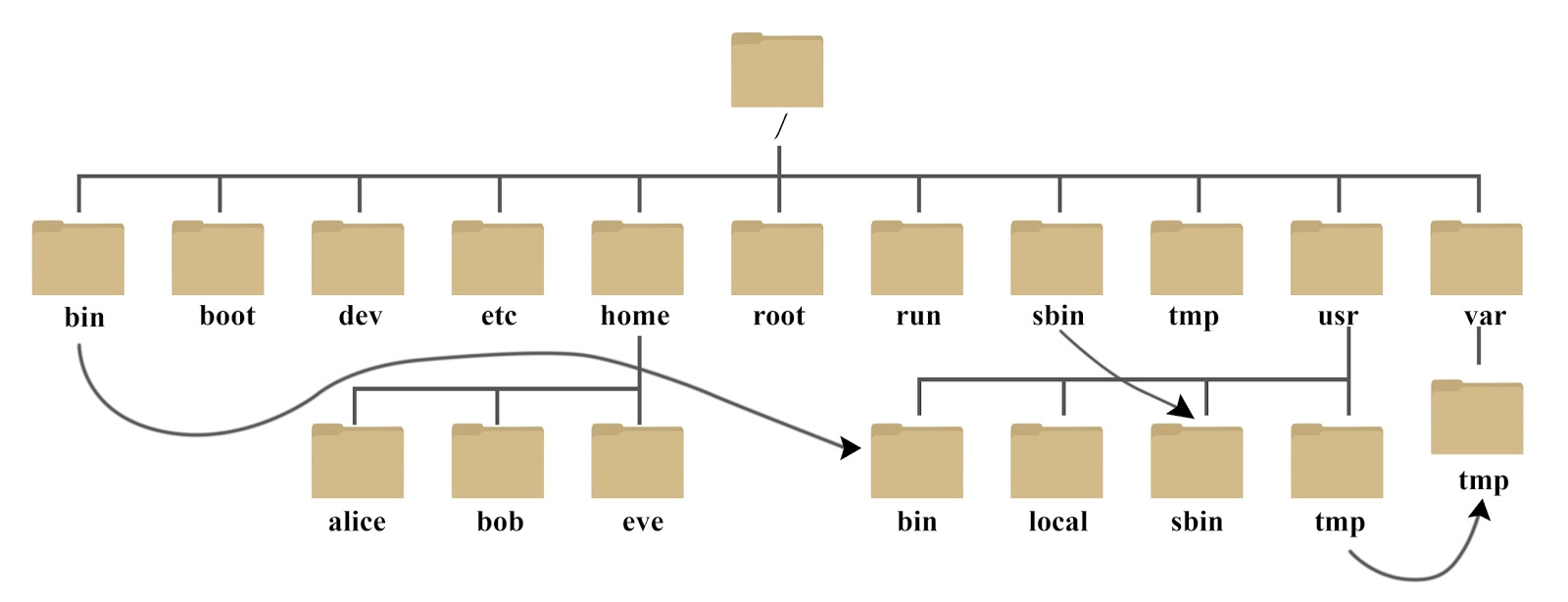
以上的共同点都是由一个 “根” 衍生出许多的 “枝干”,再从每一个 “枝干” 衍生出更多的 “叶子”。
在数据结构中,我们对树有以下称呼:
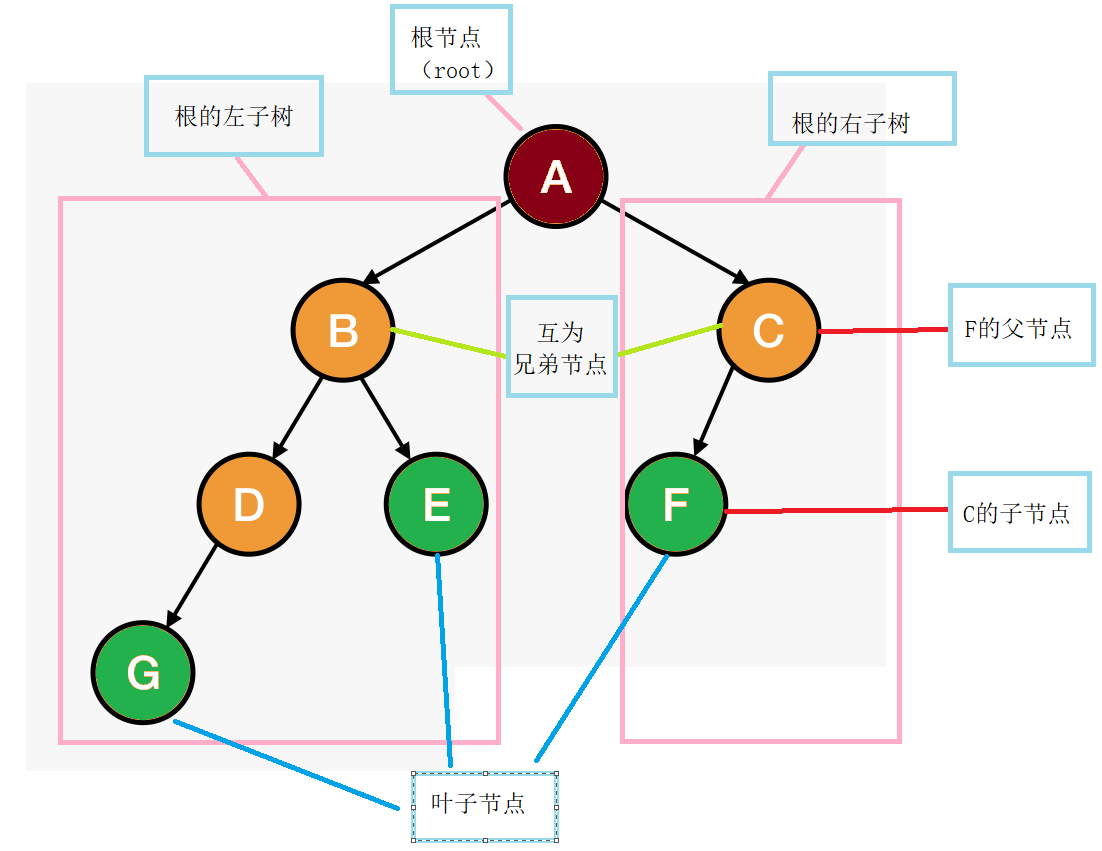
- 父节点/双亲节点:某节点的上一个节点为父节点,例如:C是F的父节点
- (孩)子节点:某一节点指向的下一个节点为子节点,例如:F是C的子节点
- 兄弟节点:父节点相同的节点互为兄弟节点,例如:D、E
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟,例如:D、F互为堂兄弟节点
- 节点的度:一个节点含有的子树的个数称为该节点的度,例如:B的度为2,C的度为1
- 叶子节点:度为0,或者无子节点的称为叶子节点,例如:G、E、F
- 树的度:一颗树中的最大的节点的度,例如:上图树的度为2
- 节点的层次:根节点为第一层, 依次类推
- 树的高度/深度:树节点的最大层次,如上图树的高度为4
- 节点的祖先:根节点到此节点的经过的所有节点都为祖先,例如:A是所有节点的祖孙
- 子孙:只要在关系在某一节点的下面都为子孙
- 森林:有(m > 0)的树所组成的集合称为森林
小结:
树的关系可以由现实生活中的亲戚关系来表示
2. 什么是二叉树?
什么是 n叉树?
n叉树,故名思意,就是树的分叉最多可以有n个。
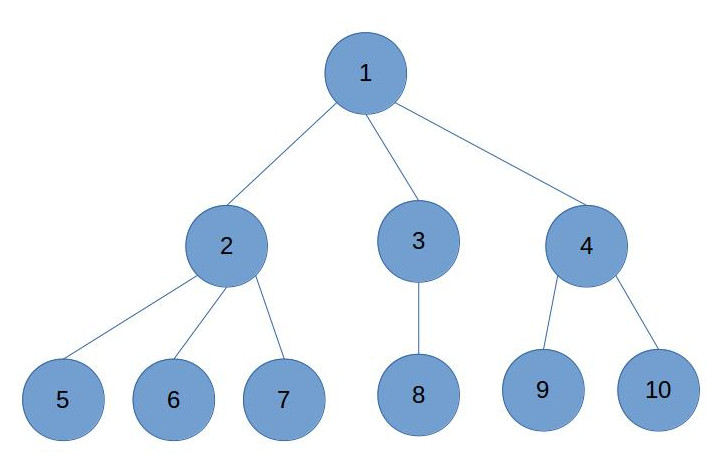
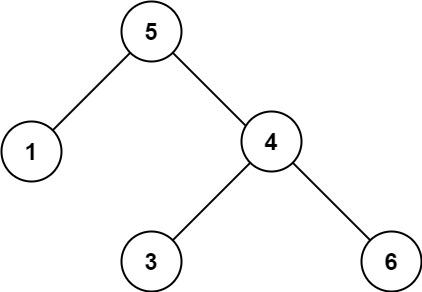
那么二叉树就是,最多有2个孩子节点的树。如下图所示。
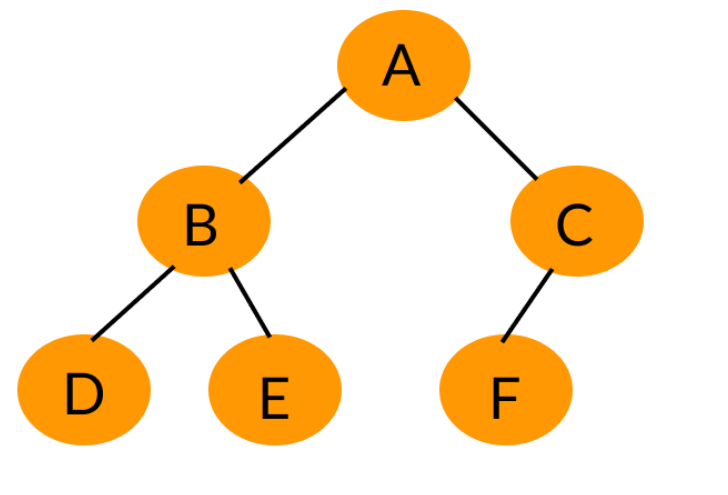
二叉树节点的两个孩子,一个被称为左孩子,一个被称为右孩子。这两个孩子的顺序是固定的。
3. 二叉树的类型
单二叉树的类型来说,其实有很多种,普通二叉树、满二叉树、完全二叉树、搜索二叉树、AVL树、红黑树……而今天我们的主题就是满二叉树和完全二叉树。
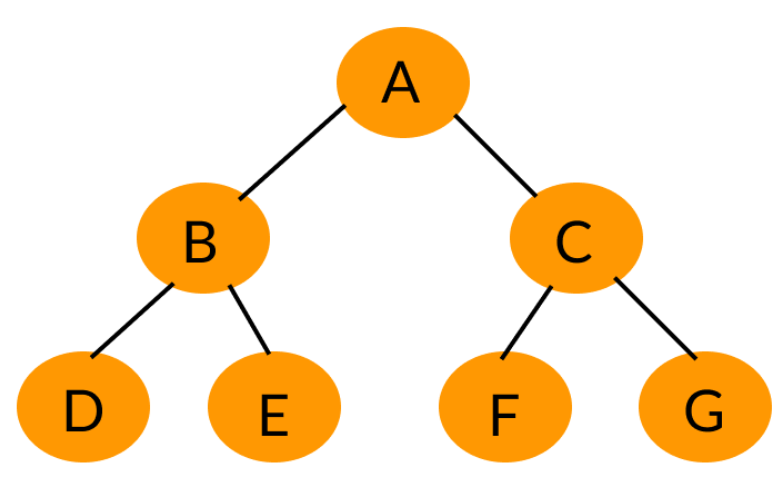
一颗二叉树的所有非叶子节点都存在左右孩子,并且所有叶子节点都在同一层级上,那么这就是满二叉树,如下图。
满二叉树的总节点数为Sn=2n−1S_n = 2^{n}-1Sn=2n−1 (n为层数)
对一个有n个节点的二叉树,按层级需要编号,则所有节点编号从1到n。如果这颗树的所有节点和同样深度的满二叉树的编号为1到n的节点位置相同,则这个二叉树为完全二叉树。如下图。(简单来说,最后一层连续排布,但不满就是完全二叉树)
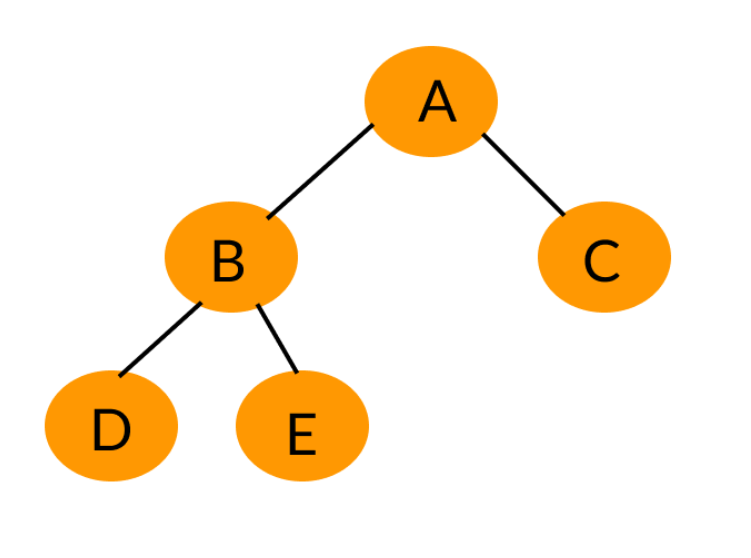
4. 二叉树的规律性质
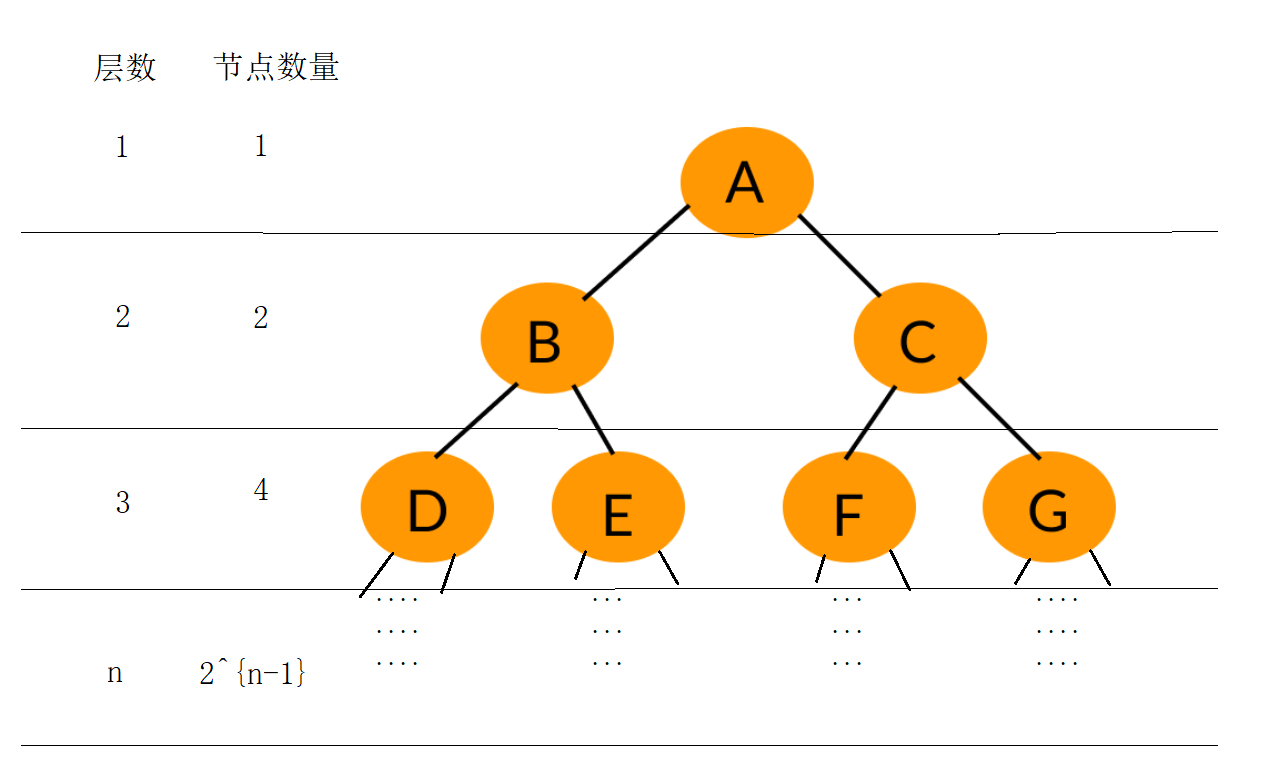
- 这是一个公比为2的等比数列,首项为1。即 a1=1a_1=1a1=1,公比 q=2q=2q=2。
- 第n层节点的数量为 2n−12^{n-1}2n−1,前n层节点的数量总和为 Sn=2n−1S_n=2^n-1Sn=2n−1。
- 对于任意一棵二叉树,满足 n=n0+n1+n2n=n_0+n_1+n_2n=n0+n1+n2,其中 nnn 为节点总数,n0n_0n0 表示度数为0的节点个数,n1n_1n1 表示度数为1的节点个数,n2n_2n2 表示度数为2的节点个数。
- 存在 n2=n0−1n_2=n_0-1n2=n0−1 的关系。
- 计算层数 nnn 的公式为 n=log2(N+1)n=\log_2(N+1)n=log2(N+1),其中 NNN 为节点总数。
上面这些规律往往会在刷题中使用到
二、二叉树的存储结构
链式结构和顺序结构是二叉树的两种常见存储方式。
1. 顺序结构
顺序存储结构使用数组作为基础存储单元,它适用于表示完全二叉树。除了堆,其他情况使用数组存储会则会造成大量空间浪费。顺序存储结构的二叉树在物理结构上是一个数组,逻辑结构上是一棵二叉树。
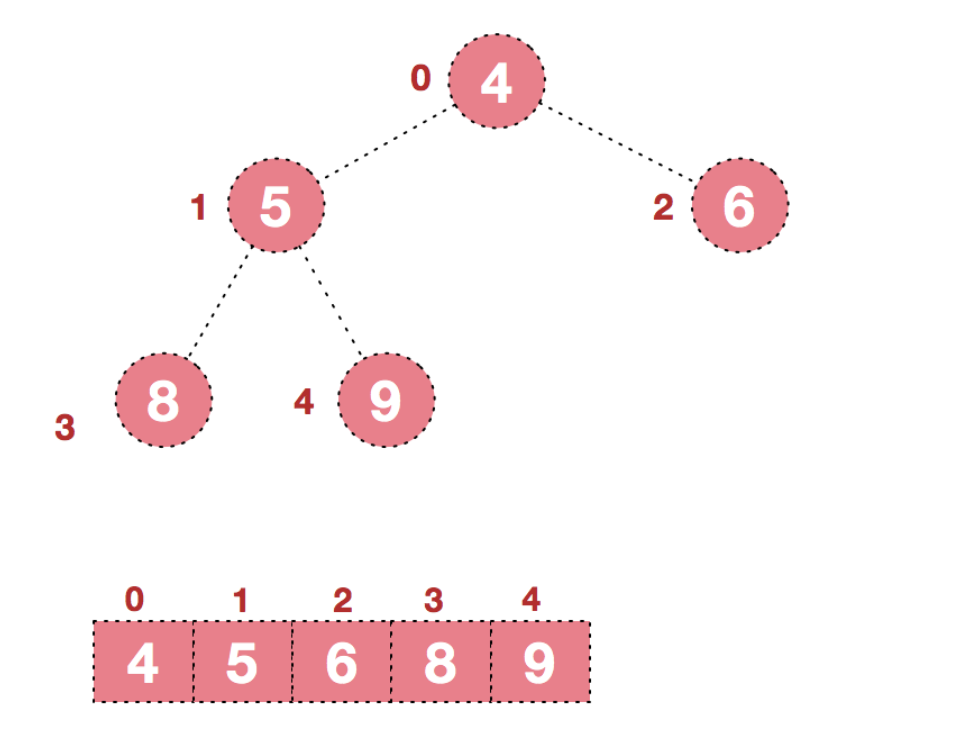
用数组来存储,我们通常会通过下标来访问元素,观察节点规律,我们不难发现:
-
若父节点为
father,子节点为child,则满足:father=child−12father = \frac{child - 1}{2}father=2child−1
-
若左右子节点分别为
left和right,并且左右孩子都存在(即 left,right≥nleft, right \ge nleft,right≥n),则满足:left=father∗2+1left = father * 2 + 1left=father∗2+1
right=father∗2+2right = father * 2 + 2right=father∗2+2
2. 链式结构
链式结构使用指针作为底层容器,通过指向子节点的指针来表示树的逻辑结构。这种方式在存储灵活性和空间利用效率方面优于顺序结构。通用方法是链表中每个节点由三个域组成:数据域和左右指针域。
typedef int treeType;//将int重定义为type_t
typedef struct TreeNode
{treeType val; //表示数据TreeNode* left; //表示左孩子TreeNode* right; //表示右孩子
}TreeNode;
(图片)
总的来说,选择使用链式结构还是顺序结构要根据具体的存储需求来决定。
三、二叉树的遍历
当我们介绍数组、链表时,为什么没有着重研究他们的遍历过程呢?
二叉树的遍历又有什么特殊之处?
在计算机程序中,遍历线性结构的数组或链表是一件简单的事情。相反,二叉树是一种典型的非线性数据结构,遍历时需要将非线性关系的节点转化为线性序列。
二叉树的遍历可以根据节点的直接位置关系分为两类:
- 深度优先遍历(前序遍历、中序遍历、后续遍历)
- 广度优先遍历(层序遍历)
下面就来看看这些不同的遍历方式吧ο(=•ω<=)ρ⌒☆
1. 深度优先遍历
- 前序遍历
二叉树的前序遍历,遍历顺序为根节点、左子树、右子树,当遇到空指针NULL时返回。
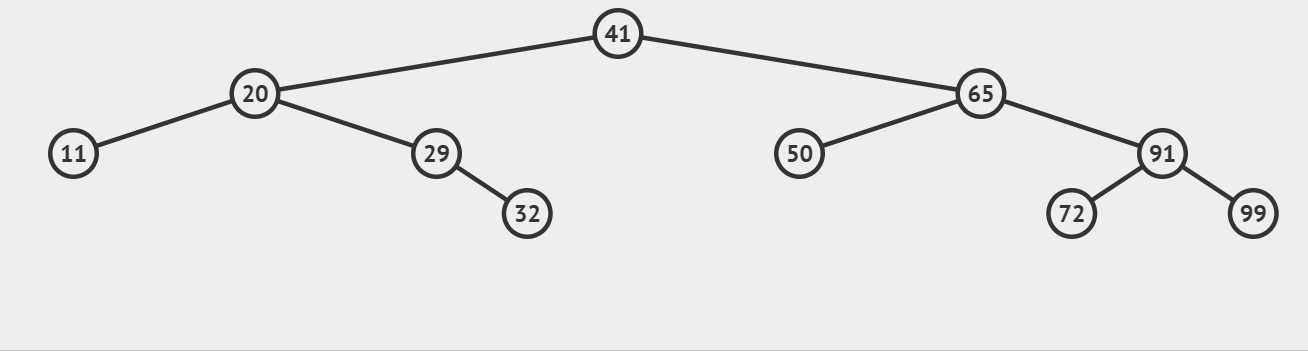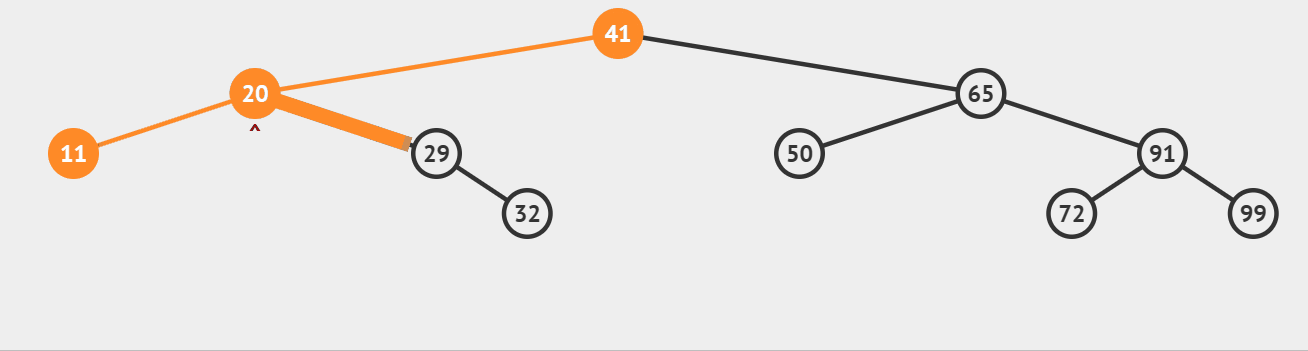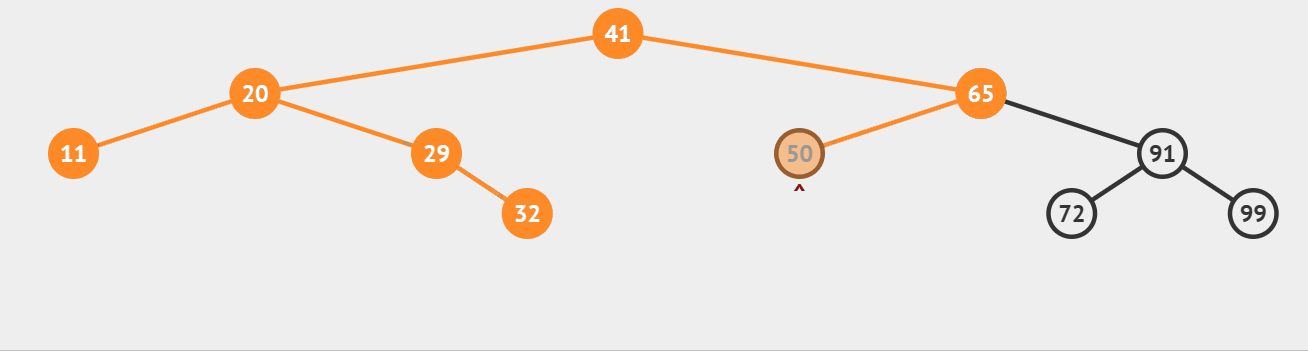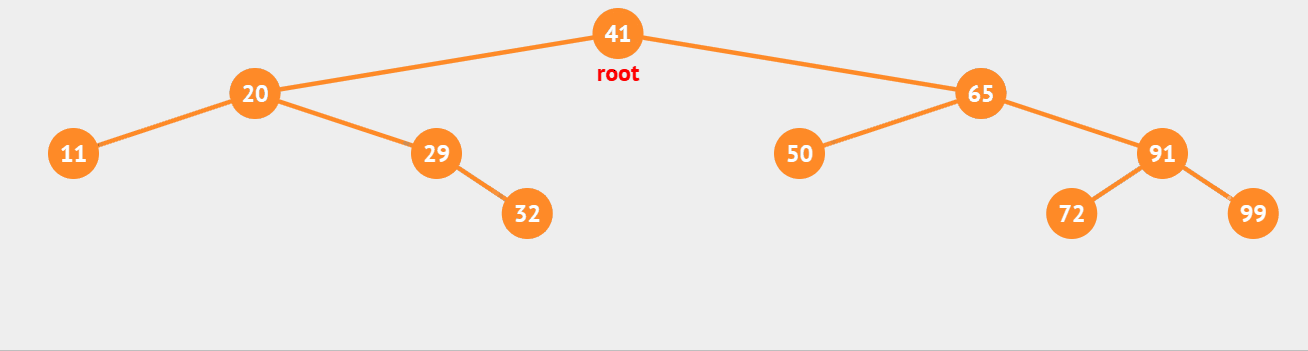
代码示例如下:
void PreOrder(TreeNode* root)
{if (root == NULL){return;}//先取出当前节点元素,再对其进行相关操作printf("%d", root->val);InOrder(root->left);//遍历左节点InOrder(root->right);//遍历右节点
}
- 中序遍历
二叉树的中序遍历,遍历顺序为左子树、根节点、右子树,当遇到空指针NULL时返回。
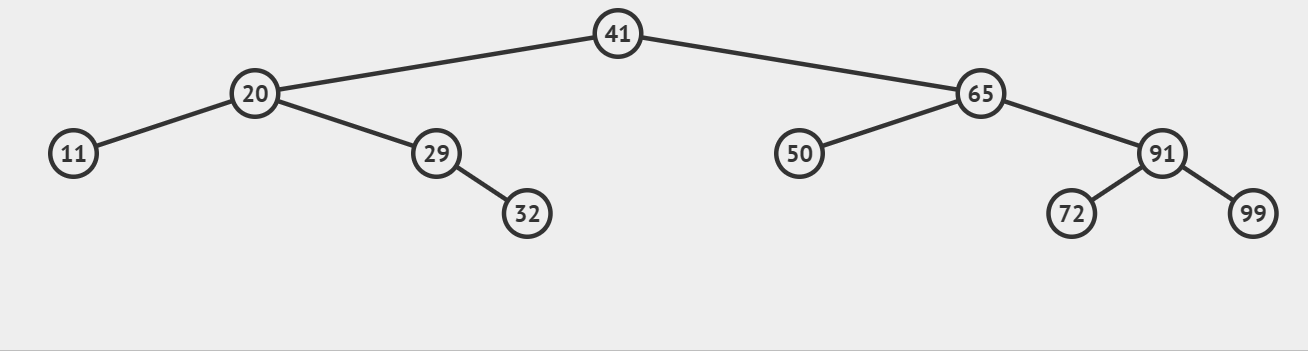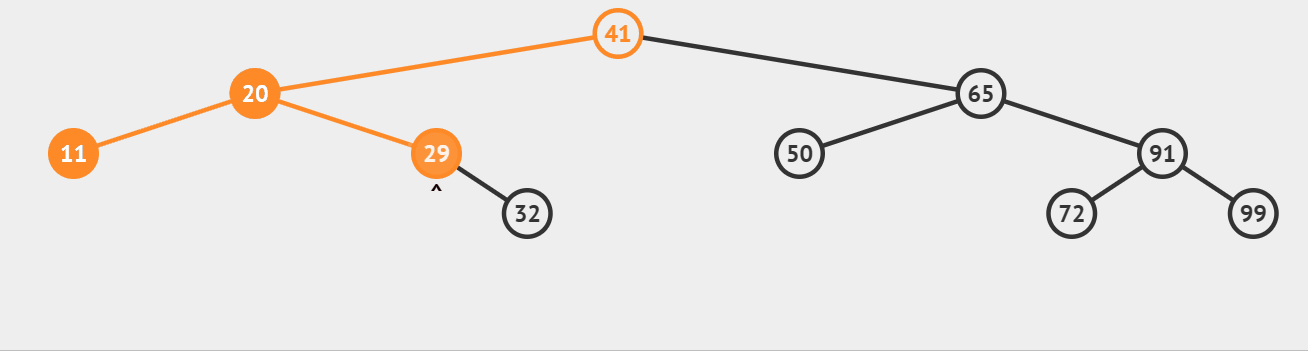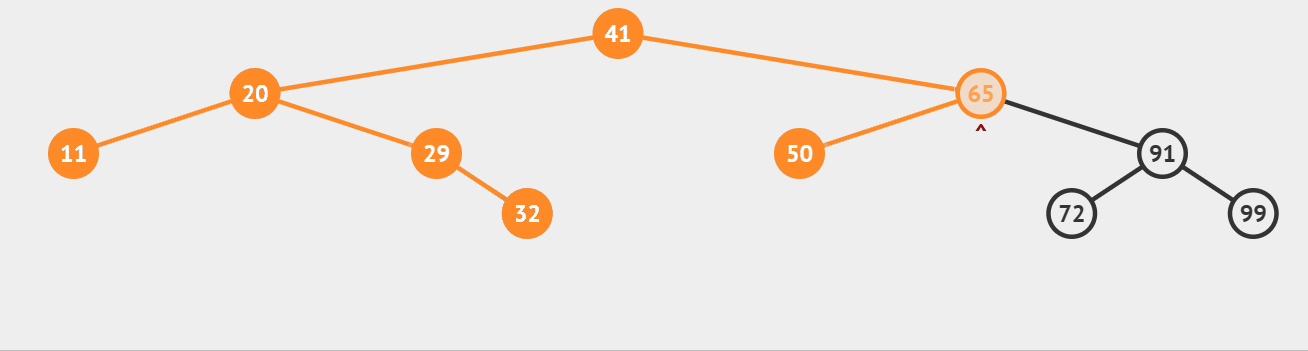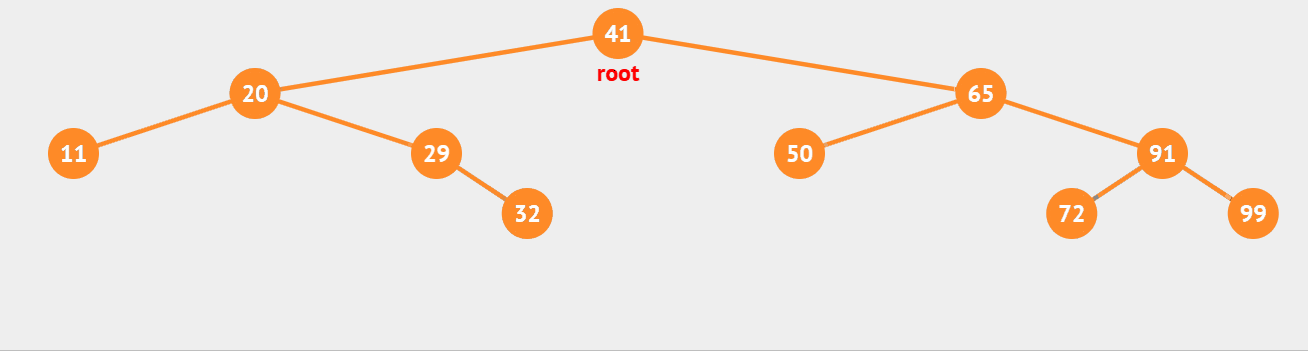
代码示例如下:
void InOrder(TreeNode* root)
{if (root == NULL){return;}InOrder(root->left);//遍历左子树printf("%d", root->val);//取出元素,进行操作InOrder(root->right);//遍历右子树
}
- 后序遍历
二叉树的后序遍历,遍历顺序为左子树、右子树、根节点,当遇到空指针NULL时返回。
代码示例如下:
void PostOrder(TreeNode* root)
{if (root == NULL){return;}PostOrder(root->left);//遍历左子树PostOrder(root->right);//遍历右子树printf("%d", root->val);//取出元素,进行操作
}
2. 广度优先遍历
广度优先遍历,按层次遍历,从根节点开始,按从上至下,从左至右的顺序遍历二叉树的所有节点。
使用广度优先算法,我们通常需要借用队列这个数据结构来实现(不知道队列的,或者没看过这篇文章的,赶紧取看看🚀传送门
接下来我们就会使用队列来完成我们所需要的操作。
这是上一期的队列节点结构,我们需要把QueueType的类型改为TreeNode*来存放我们的节点:
typedef TreeNode* QueueType;//改为TreeNode*typedef struct QueueNode
{QueueType value;struct QueueNode* next;
}QueueNode;
而这也就是为什么我们需要对类型typedef的原因,可以方便我们做修改φ(゜▽゜*)♪
遍历代码示例如下:
void LevelOrder(TreeNode* root)
{Queue q;queue_init(&q);queue_push(&q, root);while (!queue_empty(&q)){TreeNode* cur = queue_front(&q);queue_pop(&q);if (cur == NULL){continue;}printf("%d", cur->val);//取出元素,进行操作queue_push(&q, cur->left);queue_push(&q, cur->right);}//不要忘了释放Queuequeue_destory(&q);
}
在刷题过程中,单纯只是这样,多半会有些不够,接下来我们就把代码进一步优化吧:
void LevelOrder(TreeNode* root)
{Queue q;queue_init(&q);int level = 0; //表示当前层数<------------queue_push(&q, root);while (!queue_empty(&q)){TreeNode* cur = queue_front(&q);queue_pop(&q);//--------------------------------------------------int level_size = queue_size(&q);//获取当前层的元素个数for (int i = 0; i<level_size; ++i){printf("%d", cur->val);//取出元素,进行操作//对当前节点的左右子节点进行判断,若为空便没有必要入队列if (cur->left != NULL){queue_push(&q, cur->left);}if (cur->right != NULL){queue_push(&q, cur->right);}}
//---------------------------------------------------++level;//层数+1 <------------}//不要忘了释放Queuequeue_destory(&q);
}
当每一层入完队列之后,队列内的元素个数一定是下一层的元素个数(可以简单的画一个图来看看,这里就给大家布置一个小问题,让你们自己来理解吧(*^-^*)
四、小结
二叉树是树形结构的一种,其中每个节点最多有两个子节点。二叉树有多种遍历方法,包括深度优先遍历和广度优先遍历。
深度优先遍历有三种:
- 前序遍历
- 中序遍历
- 后序遍历
分别对应的遍历顺序为:
-
根节点、左子树、右子树
-
左子树、根节点、右子树
-
左子树、右子树、根节点
广度优先遍历的遍历顺序是从上到下、从左到右。
点赞是对博主的鼓励和支持!🤗 希望你们看完这篇博客后,不妨给博主一个大大的三连👍,表示对内容的赞赏!😊 当然,如果你是真心被内容打动,那么点个四连甚至五连都是博主最大的动力!💪 让我们一起用简单幽默的语气,为点赞助力!ο(=•ω<=)ρ⌒☆
题,让你们自己来理解吧(*^-^*)
相关文章:

【(C语言)数据结构奋斗100天】二叉树(上)
【(C语言)数据结构奋斗100天】二叉树(上) 🏠个人主页:泡泡牛奶 🌵系列专栏:数据结构奋斗100天 本期所介绍的是二叉树,那么什么是二叉树呢?在知道答案之前,请大家思考一下…...
Java 验证二叉搜索树
验证二叉搜索树中等给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。有效 二叉搜索树定义如下:节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。示例 1&…...

C/C++单项选择题标准化考试系统[2023-02-09]
C/C单项选择题标准化考试系统[2023-02-09] ©3.17 单项选择题标准化考试系统 【难度系数】5级 【任务描述】 设计一个单项选择题的考试系统,可实现试题维护、自动组卷等功能。 【功能描述】 (1)管理员功能: 试题管理:每个试题包括题干、四个备选答案标准答案…...
爱了爱了,这些顶级的 Python 工具包太棒了
Python 语言向来以丰富的第三方库而闻名,今天来介绍几个非常nice的库,有趣好玩且强大!推荐好好学习。 文章目录技术交流数据采集AKShareTuShareGoPUPGeneralNewsExtractor爬虫playwright-pythonawesome-python-login-modelDecryptLoginScylla…...
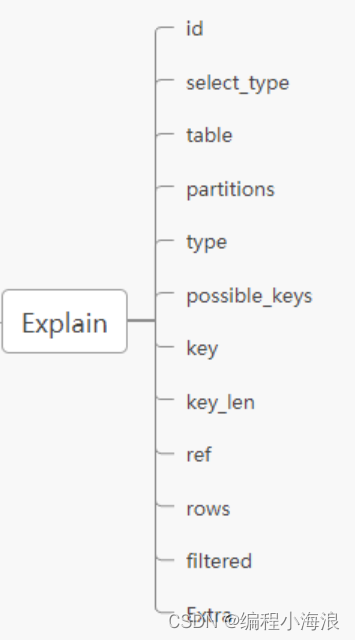
【Explain详解与索引优化最佳实践】
摘要 explain命令是查看MySQL查询优化器如何执行查询的主要方法,可以很好的分析SQL语句的执行情况。每当遇到执行慢(在业务角度)的SQL,都可以使用explain检查SQL的执行情况,并根据explain的结果相应的去调优SQL等。 …...
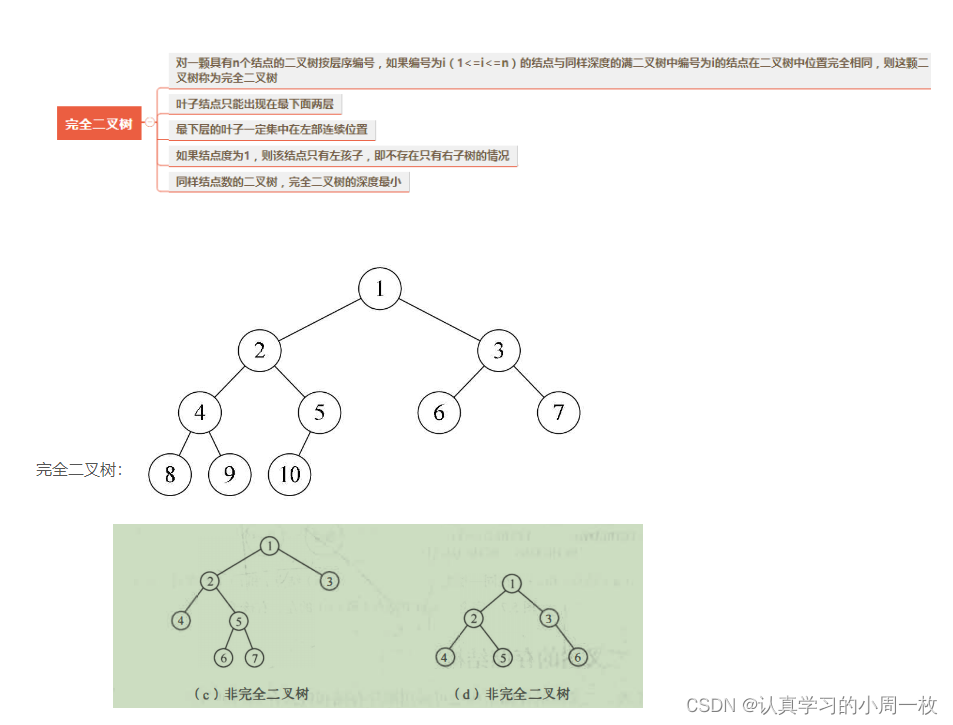
【树和二叉树】数据结构二叉树和树的概念认识
前言:在之前,我们已经把栈和队列的相关概念以及实现的方法进行了学习,今天我们将认识一个新的知识“树”!!! 目录1.树概念及结构1.1树的概念1.2树的结构1.3树的相关概念1.4 树的表示1.5 树在实际中的运用&a…...

通达信收费接口查询可申购新股c++源码分享
有很多股民在做股票交易时为了实现盈利会借助第三三方炒股工具帮助自己,那么通达信收费接口就是人们常用到的,今天小编来分享一下通达信收费接口查询可申购新股c源码: std::cout << " 查询可申购新股: category 12 \n"; c…...
。)
【C#设计模式】创建型设计模式 (单例,工厂)。
c# 创建型设计模式 1.单例设计模式c# 单例JS 单例(ES6)c# 扩展方法c# 如果窗体非单例(tips:窗口可以容器化)2.工厂设计模式JS 简单工厂(ES6)C# 简单工厂C# params关键词(自定义参数个数)JS 手写JQuery(委托,工厂方式隐藏细节)JS ...四种用法C# 偷懒工厂1.单例设计模式 …...
Ubuntu 22.04 LTS 入门安装配置优化、开发软件安装一条龙
Ubuntu 22.04 LTS 入门安装配置&优化、开发软件安装 例行前言 最近在抉择手上空余的笔记本(X220 i7-2620M,Sk Hynix ddr3 8G*2 ,Samsung MINISATA 256G)拿来运行什么系统比较好,早年间我或许还会去继续使用Win…...
第五十章 动态规划——数位DP模型
第五十章 动态规划——数位DP模型一、什么是数位DP数位DP的识别数位DP的思路二、例题1、AcWing 1083. Windy数(数位DP)2、AcWing 1082. 数字游戏(数位DP)3、AcWing 1081. 度的数量(数位DP)一、什么是数位DP…...
02- pandas 数据库 (机器学习)
pandas 数据库重点: pandas 的主要数据结构: Series (一维数据)与 DataFrame (二维数据)。 pd.DataFrame(data np.random.randint(0,151,size (5,3)), # 生成pandas数据 index [Danial,Brandon,softpo,Ella,Cindy], # 行索引 …...

学Qt想系统的学习,看哪本书?
Qt 是一个跨平台应用开发框架(framework),它是用 C语言写的一套类库。使用 Qt 能为 桌面计算机、服务器、移动设备甚至单片机开发各种应用(application),特别是图形用户界面 (graphical user in…...
)
2023年网络安全比赛--跨站脚本攻击②中职组(超详细)
一、竞赛时间 180分钟 共计3小时 二、竞赛阶段 1.访问服务器网站目录1,根据页面信息完成条件,将获取到弹框信息作为flag提交; 2.访问服务器网站目录2,根据页面信息完成条件,将获取到弹框信息作为flag提交; 3.访问服务器网站目录3,根据页面信息完成条件,将获取到弹框信息…...

网络安全实验室4.注入关
4.注入关 1.最简单的SQL注入 url:http://lab1.xseclab.com/sqli2_3265b4852c13383560327d1c31550b60/index.php 查看源代码,登录名为admin 最简单的SQL注入,登录名写入一个常规的注入语句: admin’ or ‘1’1 密码随便填,验证…...

领域搜索算法之经典The Lin-Kernighan algorithm
领域搜索算法之经典The Lin-Kernighan algorithmThe Lin-Kernighan algorithm关于算法性能提升的约束参考文献领域搜索算法是TSP问题中的三大经典搜索算法之一,另外两种分别是回路构造算法和组合算法。 而这篇文章要介绍的The Lin-Kernighan algorithm属于领域搜索算…...

深度学习基础-机器学习基本原理
本文大部分内容参考《深度学习》书籍,从中抽取重要的知识点,并对部分概念和原理加以自己的总结,适合当作原书的补充资料阅读,也可当作快速阅览机器学习原理基础知识的参考资料。 前言 深度学习是机器学习的一个特定分支。我们要想…...

C语言操作符详解 一针见血!
目录算数操作符移位操作符位操作符赋值操作符单目操作符关系操作符逻辑操作符条件操作符逗号表达式下标引用、函数调用和结构成员表达式求值11.1 隐式类型转换算数操作符💭 注意/ 除法 --得到的是商% 取模(取余)--得到的是余数如果除法操作符…...
前端面试题汇总
一:JavaScript 1、闭包是什么?利弊?如何解决弊端? 闭包是什么:JS中内层函数可以访问外层函数的变量,外层函数无法操作内存函数的变量的特性。我们把这个特性称作闭包。 闭包的好处: 隔离作用…...

以数据驱动管理场景,低代码助力转型下一站
数据驱动 数据驱动,是通过移动互联网或者其他的相关软件为手段采集海量的数据,将数据进行组织形成信息,之后对相关的信息讲行整合和提炼,在数据的基础上经过训练和拟合形成自动化的决策模型,简单来说,就是…...

2023年全国数据治理DAMA-CDGA/CDGP考试报名到弘博创新
弘博创新是DAMA中国授权的数据治理人才培养基地,贴合市场需求定制教学体系,采用行业资深名师授课,理论与实践案例相结合,快速全面提升个人/企业数据治理专业知识与实践经验,通过考试还能获得数据专业领域证书。 DAMA认…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
