Java--静态字段与静态方法
1、静态字段
如果将一个字段定义为static,每个类只有一个这样的字段。而对于非静态的实例字段,每个对象都有自己的一个副本。
例如:
class Employee
{private static int nextId = 1;private int id;...
}
其中,每一个Employee对象都有一个自己的id字段,但这个类的所有实例将共享一个nextId字段。换句话说,如果有1000个Employee类对象,则有1000个实例字段id,分别对应每一个对象。但是,只有一个静态字段nextId。即使没有Employee 对象,静态字段nextId 也存在。它属于类,而不属于任何单个的对象。
注释:
在一些面向对象程序设计语言中,静态字段被称为类字段。术语“静态”只是沿用了C++的叫法,并无实际意义。
2、静态常量
Math类中的一个静态常量
public class Math
{...public static final PI = 3.1415926535897932846;...
}
在程序中用Math.PI来访问这个变量。
如果省略关键字static, PI 就变成了Math 类的一一个实例字段。也就是说,需要通过Math类的一个对象来访问PI,并且每一一个Math对象都有它自己的一个PI副本。
System类中你的一个静态常量
public class System
{...public static final PrntStream out = ...;...
}
静态常量只能访问,不能直接修改。
如:
System.out = new PrintStream(...); // ERROR--out is final
3、静态方法
静态方法是不在对象上执行的方法。例如,Math类中pow方法就是一个静态方法。表达式:Math.pow(x,a).
Employee类的静态方法不能访问id实例字段,因为它不能在对象上执行操作。但是,静态方法可以访问静态字段。
示例:
public static int getNextId()
{return nextId; //返回静态字段
}
可以直接用类名调用该方法:
int n = Employee.getNextId();
在下面两种情况下可以使用静态方法:
- 方法不需要访问对象状态,因为它需要的所有参数都通过显式参数提供(例如:(Math.pow)。
- 方法只需要访问类的静态字段( 例如: Employee . getNextId)。
4、main方法
需要注意,可以调用静态方法而不需要任何对象。例如,不需要构造Math类的任何对象就可以调用Math,pow。同理,main 方法也是-一个静态方法。
public class Applicationpublic static void main(String[] args)// construct objects here...}
}
main方法不对任何对象进行操作。事实上,在启动程序时还没有任何对象。静态的main方法将执行并构造程序所需要的对象。
提示:
每一个类可以有一个main方法。这是常用于对类进行单元测试的一个技巧。例如,可以在Employee类中添加一个main方法:
class Employee public Employee(String n, double s, int year, int month, int day) {name = n;salary = s;hireDay = LocalDate. of(year, month, day); } public static void main(String[] args) // unit test {var e = new Employee("Romeo", 50000, 2003, 3, 31);e.raiseSalary(10);System.out . println(e.getName() +""+ e.getSalary()); }如果想要独立地测试Employee类,只需要执行
java Employee如果Employee类是一个更大型应用程序的一部分,就可以使用下面这条语句运行程序
java ApplicationEmployee类中的main方法永远不会执行
相关文章:

Java--静态字段与静态方法
1、静态字段 如果将一个字段定义为static,每个类只有一个这样的字段。而对于非静态的实例字段,每个对象都有自己的一个副本。 例如: class Employee {private static int nextId 1;private int id;... }其中,每一个Employee对…...
多线程的五种“打开”方式
1 概念 1.1 线程是什么?? 线程(Thread)是计算机科学中的一个基本概念,它是进程(Process)中的一个执行单元,负责执行程序的指令序列。线程是操作系统能够进行调度和执行的最小单位。…...

信息熵 条件熵 交叉熵 联合熵 相对熵(KL散度) 互信息(信息增益)
粗略版快速总结 条件熵 H ( Q ∣ P ) 联合熵 H ( P , Q ) − H ( P ) 条件熵H(Q∣P)联合熵H(P,Q)−H(P) 条件熵H(Q∣P)联合熵H(P,Q)−H(P) 信息增益 I ( P , Q ) H ( P ) − H ( P ∣ Q ) H ( P ) H ( Q ) − H ( P , Q ) 信息增益 I(P,Q)H(P)−H(P∣Q)H(P)H(Q)-H(P,Q) 信息…...

Fiddler Response私人订制
在客户端接口的测试中,我们经常会需要模拟各种返回状态或者特定的返回值,常见的是用Fiddler模拟各种请求返回值场景,如重定向AutoResponder、请求拦截修改再下发等等。小编在近期的测试中遇到的一些特殊的请求返回模拟的测试场景,…...
【德哥说库系列】-ASM管理Oracle 19C单实例部署
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...
手写一个简单爬虫--手刃豆瓣top250排行榜
#拿到页面面源代码 request #通过re来提取想要的有效信息 re import requests import re url"https://movie.douban.com/top250"headers{"user-agent":"Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/11…...
【word密码】如何限制word文件中部分内容?
Word文件中有一部分内容不想他人编辑,我们可以设置限制编辑,可以对一部分内容设置限制编辑,具体方法如下: 我们将需要将可以编辑的地方选中,然后打开限制编辑功能 然后勾选限制编辑设置界面中的【限制编辑】和【每个人…...

spring 自定义类型转换-ConverterRegistry
1背景介绍 一个应用工程里面,一遍会涉及到很多的模型转换,如DTO模型转DO模型,DO模型转DTO, 或者Request转DTO模型,总的来说,维护起来还是相对比较复杂。每涉及一个转换都需要重新写对应类的get或者set方法,…...

springboot实现发送短信验证码
目录 一、选择并注册短信服务提供商: 二、添加依赖: 三、配置短信服务信息: 四、编写发送短信验证码的方法: 五、调用发送短信验证码的方法: 一、选择并注册短信服务提供商: 1、选择一个可靠的短信服…...

2024王道408数据结构P144 T18
2024王道408数据结构P144 T18 思考过程 首先还是先看题目的意思,让我们在中序线索二叉树里查找指定结点在后序的前驱结点,这题有一点难至少对我来说…我讲的不清楚理解一下我做的也有点糊涂。在创建结构体时多两个变量ltag和rtag,当ltag0时…...

在windows下安装配置skywalking
1.下载地址 Downloads | Apache SkyWalkinghttp://skywalking.apache.org/downloads/ 2.文件目录说明 将文件解压后,可看到agent和bin目录: Agent:作为探针,安装在服务器端,进行数据采集和上报。 Config:…...
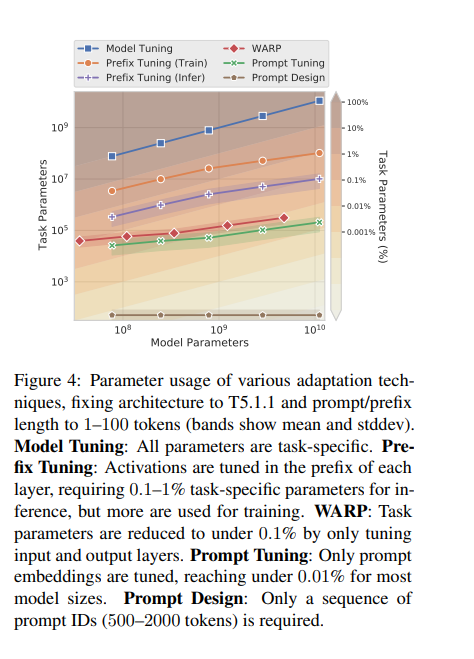
关于大模型参数微调的不同方法
Adapter Tuning 适配器模块(Adapter Moudle)可以生成一个紧凑且可扩展的模型;每个任务只需要添加少量可训练参数,并且可以在不重新访问之前任务的情况下添加新任务。原始网络的参数保持不变,实现了高度的参数共享 Pa…...
)
方法的引用第一版(method reference)
1、体验方法引用 在使用Lambda表达式的时候,我们实际上传递进去的代码就是一种解决方案:拿参数做操作那么考虑一种情况:如果我们在Lanbda中所指定的操作方案,已经有地方存在相同方案,那是否还有必要再重复逻辑呢&#…...

Android DataBinding 基础入门(学习记录)
目录 一、DataBinding简介二、findViewById 和 DataBinding 原理及优缺点1. findViewById的优缺点2. DataBinding的优缺点 三、Android mvvm 之 databinding 原理1. 简介和三个主要的实体DataViewViewDataBinding 2.三个功能2.1. rebind 行为2.2 observe data 行为2.3 observe …...

spring 错误百科
一、使用Spring出错根源 1、隐式规则的存在 你可能忽略了 Sping Boot 中 SpringBootApplication 是有一个默认的扫描包范围的。这就是一个隐私规则。如果你原本不知道,那么犯错概率还是很高的。类似的案例这里不再赘述。 2、默认配置不合理 3、追求奇技淫巧 4、…...
OpenCV基本操(IO操作,读取、显示、保存)
图像的IO操作,读取和保存方法 1.1 API cv.imread()参数: 要读取的图像 读取图像的方式: cv.IMREAD*COLOR:以彩色模式加载图像,任何图像的图像的透明度都将被忽略。这是默认参数 标志: 1 cv.IMREAD*GRAYSCALE :以…...

1.快速搭建Flask项目
一.Pear Admin Flask 官网文档:http://www.pearadmin.com/doc/index.html 1.1下载安装 # 下 载 git clone https://gitee.com/pear-admin/pear-admin-flask# 安 装 pip install -r requirements.txt1.2修改配置 applications下的config.py docker运行的修改dockerdata/conf…...

编程题四大算法思想(三)——贪心法:找零问题、背包问题、任务调度问题、活动选择问题、Prim算法
文章目录 贪心法找零问题(change-making problem)贪心算法要求基本思想适合求解问题的特征 背包问题0/1背包问题0/1背包问题——贪心法 分数背包问题 任务调度问题活动选择问题活动选择——贪心法最早结束时间优先——最优性证明 Prim算法 贪心法 我在当…...
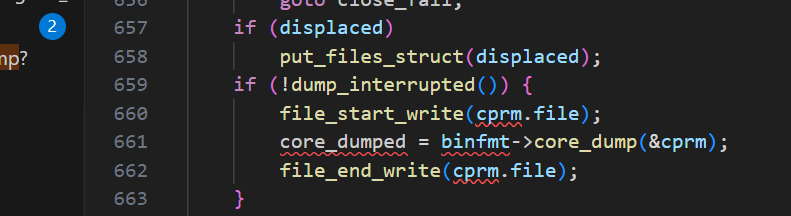
core dump管理在linux中的前世今生
目录 一、什么是core dump? 二、coredump是怎么来的? 三、怎么限制coredump文件的产生? ulimit 半永久限制 永久限制 四、从源码分析如何对coredump文件的名字和路径管理 命名 管理 一些问题的答案 1、为什么新的ubuntu不能产生c…...

Springboot整合knife4j配置swagger教程-干货
开启swagger文档,直接上教程。 第一步:引入依赖 <!--swagger 依赖--><dependency><groupId>com.github.xiaoymin</groupId><artifactId>knife4j-spring-boot-starter</artifactId><version>3.0.3</version></d…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
