代码随想录算法训练营 day59|503.下一个更大元素II、42. 接雨水
一、503.下一个更大元素II
力扣题目链接
可以不扩充nums,在遍历的过程中模拟走两边nums
class Solution {
public:vector<int> nextGreaterElements(vector<int>& nums) {vector<int> result(nums.size(), -1);if (nums.size() == 0) return result;stack<int> st;st.push(0);for (int i = 1; i < nums.size() * 2; i++) { // 模拟遍历两边nums,注意一下都是用i % nums.size()来操作if (nums[i % nums.size()] < nums[st.top()]) st.push(i % nums.size());else if (nums[i % nums.size()] == nums[st.top()]) st.push(i % nums.size()); else {while (!st.empty() && nums[i % nums.size()] > nums[st.top()]) {result[st.top()] = nums[i % nums.size()];st.pop();}st.push(i % nums.size());}}return result;}
};二、42. 接雨水
力扣题目链接
1)双指针法
把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight),避免了重复计算。
当前位置,左边的最高高度是前一个位置的左边最高高度和本高度的最大值。
即从左向右遍历:maxLeft[i] = max(height[i], maxLeft[i - 1]);
从右向左遍历:maxRight[i] = max(height[i], maxRight[i + 1]);
class Solution {
public:int trap(vector<int>& height) {if (height.size() <= 2) return 0;vector<int> maxLeft(height.size(), 0);vector<int> maxRight(height.size(), 0);int size = maxRight.size();// 记录每个柱子左边柱子最大高度maxLeft[0] = height[0];for (int i = 1; i < size; i++) {maxLeft[i] = max(height[i], maxLeft[i - 1]);}// 记录每个柱子右边柱子最大高度maxRight[size - 1] = height[size - 1];for (int i = size - 2; i >= 0; i--) {maxRight[i] = max(height[i], maxRight[i + 1]);}// 求和int sum = 0;for (int i = 0; i < size; i++) {int count = min(maxLeft[i], maxRight[i]) - height[i];if (count > 0) sum += count;}return sum;}
};2)单调栈解法
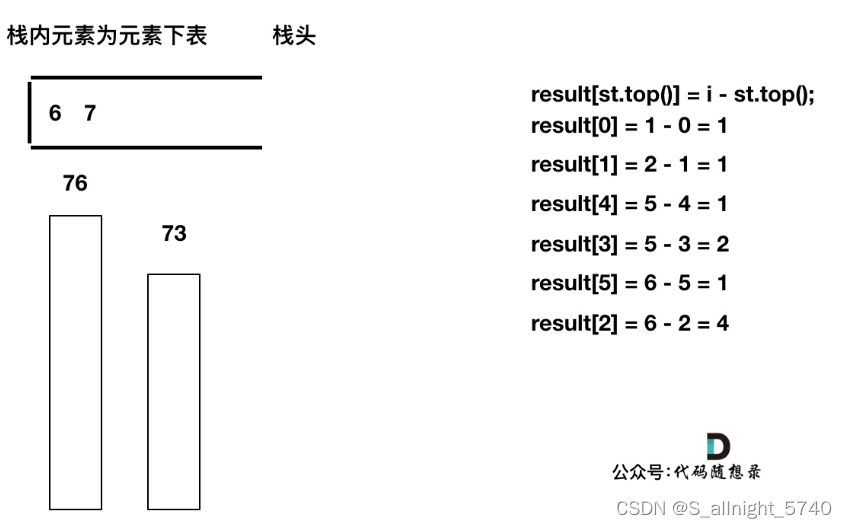
class Solution {
public:int trap(vector<int>& height) {if (height.size() <= 2) return 0; // 可以不加stack<int> st; // 存着下标,计算的时候用下标对应的柱子高度st.push(0);int sum = 0;for (int i = 1; i < height.size(); i++) {if (height[i] < height[st.top()]) { // 情况一st.push(i);} if (height[i] == height[st.top()]) { // 情况二st.pop(); // 其实这一句可以不加,效果是一样的,但处理相同的情况的思路却变了。st.push(i);} else { // 情况三while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是whileint mid = st.top();st.pop();if (!st.empty()) {int h = min(height[st.top()], height[i]) - height[mid];int w = i - st.top() - 1; // 注意减一,只求中间宽度sum += h * w;}}st.push(i);}}return sum;}
};
相关文章:

代码随想录算法训练营 day59|503.下一个更大元素II、42. 接雨水
一、503.下一个更大元素II 力扣题目链接 可以不扩充nums,在遍历的过程中模拟走两边nums class Solution { public:vector<int> nextGreaterElements(vector<int>& nums) {vector<int> result(nums.size(), -1);if (nums.size() 0) return…...

MyBatis数据库操作
文章目录 前言一、MyBatis的各种查询功能1.查询一个实体类对象2.查询一个List集合3.查询单个数据4.查询一条数据为map集合5.查询多条数据为map集合方法一方法二 6.测试类 二、特殊SQL的执行1.模糊查询2.批量删除3.动态设置表名5.添加功能获取自增的主键6.测试类 三、自定义映射…...

python flask框架 debug功能
从今天开始,准备整理一些基础知识,分享给需要的人吧 先整理个flask的debug功能,首先列举一下debug加与不加的区别,然后再上代码和图看看差异 区别: (1)加了debug后,修改js…...

《深入浅出OCR》第六章:OCR数据集与评价指标
一、OCR技术流程 在介绍OCR数据集开始,我将带领大家和回顾下OCR技术流程,典型的OCR技术pipline如下图所示,其中,文本检测和识别是OCR技术的两个重要核心技术。 1.1 图像预处理: 图像预处理是OCR流程的第一步…...
15. 线性代数 - 克拉默法则
文章目录 克拉默法则矩阵运算Hi,大家好。我是茶桁。 上节课我们在最后提到了一个概念「克拉默法则」,本节课,我们就来看看到底什么是克拉默法则。 克拉默法则 之前的课程我们一直在强调,矩阵是线性方程组抽象的来的。那么既然我们抽象出来了,有没有一种比较好的办法高效…...
【LeetCode】剑指 Offer <二刷>(6)
目录 题目:剑指 Offer 12. 矩阵中的路径 - 力扣(LeetCode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 13. 机器人的运动范围 - 力扣&#…...
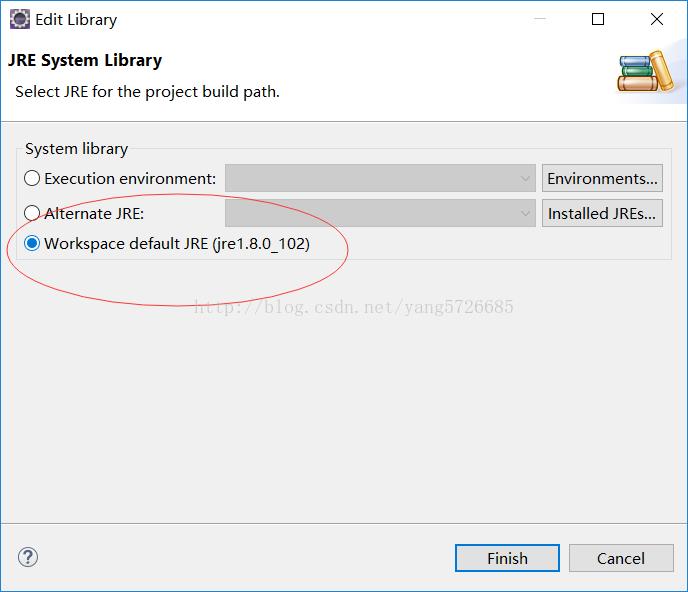
jsp页面出现“String cannot be resolved to a type”错误解决办法
篇首语:小编为大家整理,主要介绍了jsp页面出现“String cannot be resolved to a type”错误解决办法相关的知识,希望对你有一定的参考价值。 jsp页面出现“String cannot be resolved to a type”错误解决办法 解决办法: 右键项目…...

【go-zero】使用自带Redis方法
yaml配置文件 RedisS:Host: Type: Pass: config增加 RedisS struct {Host stringType stringPass string}svc文件 type * struct {RedisClient *redis.Redis } func *(c config.Config) * {sqlConn : sqlx.NewMysql(c.DB.DataSource)return &*{RedisClient: redis.New(c…...
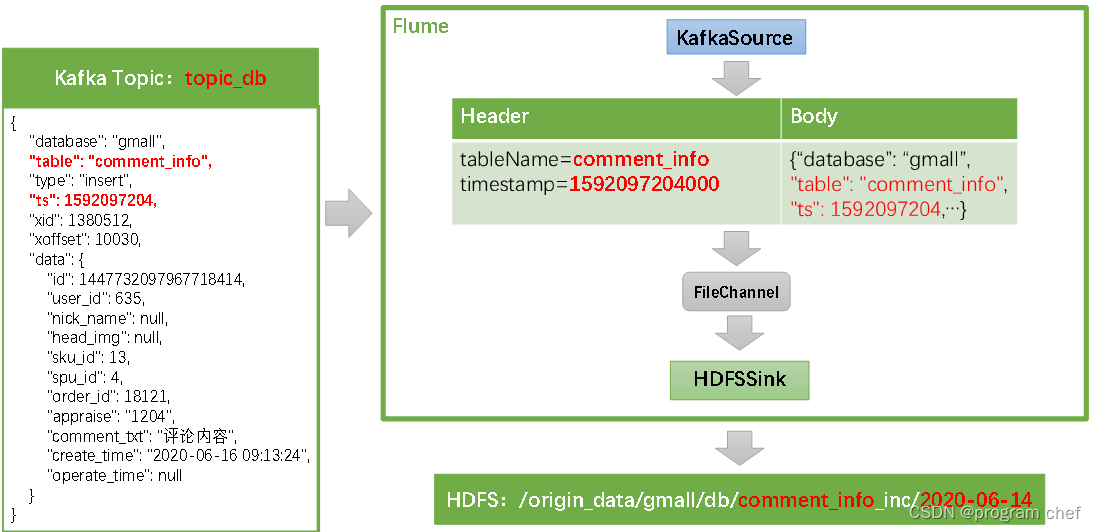
离线数仓同步数据3
业务数据_增量表数据同步 1)Flume配置概述2)Flume配置实操3)通道测试4)编写Flume启停脚本 1)Flume配置概述 Flume需要将Kafka中topic_db主题的数据传输到HDFS,故其需选用KafkaSource以及HDFSSinkÿ…...
Prometheus+Grafana 搭建应用监控系统
一、背景 完善的监控系统可以提高应用的可用性和可靠性,在提供更优质服务的前提下,降低运维的投入和工作量,为用户带来更多的商业利益和客户体验。下面就带大家彻底搞懂监控系统,使用Prometheus Grafana搭建完整的应用监控系统。 …...

Spring Boot整合Log4j2.xml的问题
文章目录 问题解决参考 问题 Spring Boot整合Log4j2.xml的时候返回以下错误: Caused by: org.apache.logging.log4j.LoggingException: log4j-slf4j-impl cannot be present with log4j-to-slf4j 进行了解决。 解决 Spring Boot整合Log4j2.xml经过以下操作&#…...
代码随想录算法训练营第五十八天 | 739. 每日温度,496.下一个更大元素 I
代码随想录算法训练营第五十八天 | 739. 每日温度,496.下一个更大元素 I 739. 每日温度496.下一个更大元素 I 739. 每日温度 题目链接 视频讲解 给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answe…...

【动手学深度学习】--文本预处理
文章目录 文本预处理1.读取数据集2.词元化3.词表4.整合所有功能 文本预处理 学习视频:文本预处理【动手学深度学习v2】 官方笔记:文本预处理 对于序列数据处理问题,在【序列模型】中评估了所需的统计工具和预测时面临的挑战,这…...

2023年最佳研发管理平台评选:哪家表现出色?
“研发管理平台哪家好?以下是一些知名的研发管理软件品牌:Zoho Projects、JIRA、Trello、Microsoft Teams、GitLab。’” 企业需要不断创新以保持竞争力。研发是企业创新的核心,而研发管理平台则为企业提供了一个有效的工具来支持和管理其研发…...

轻量容器引擎Docker基础使用
轻量容器引擎Docker Docker是什么 Docker 是一个开源项目,诞生于 2013 年初,最初是 dotCloud 公司内部的一个业余项目。 它基于 Google 公司推出的 Go 语言实现,项目后来加入了 Linux 基金会,遵从了 Apache 2.0 协议,…...

questions
1.JDK 和 JRE 有什么区别? JDK:Java Development Kit 的简称,java 开发工具包,提供了 java 的开发环境和运行环境 JRE:Java Runtime Environment 的简称,java 运行环境,为 java 的运行提供了所需…...
MojoTween:使用「Burst、Jobs、Collections、Mathematics」优化实现的Unity顶级「Tween动画引擎」
MojoTween是一个令人惊叹的Tween动画引擎,针对C#和Unity进行了高度优化,使用了Burst、Jobs、Collections、Mathematics等新技术编码。 MojoTween提供了一套完整的解决方案,将Tween动画应用于Unity Objects的各个方面,并可以通过E…...

Vue3响应式源码实现
Vue3响应式源码实现 初始化项目结构 vue-proxy ├── effect.js ├── effect.ts ├── index.html ├── index.js ├── package.json ├── reactive.js ├── reactive.ts └── webpack.config.jsreactive.ts import { track, trigger } from "./effect&q…...

【RapidAI】P1 中文文本切割程序
中文文本切割程序 基本信息代码解析相关包获取 yaml 关键文件类的构造函数切分语句部分特殊处理 PDF重点切分去除数组中空字符串再度切分后长度 附录附录一:完整代码附录二:可继续思考问题 基本信息 文件名: chinese_text_splitter.py 文件地…...

4、QT中的网络编程
一、Linux中的网络编程 1、子网和公网的概念 子网网络:局域网,只能进行内网的通信公网网络:因特网,服务器等可以进行远程的通信 2、网络分层模型 4层模型:应用层、传输层、网络层、物理层 应用层:用户自…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
