MATLAB/Simulink 通信原理及仿真学习(三)
文章目录
- MATLAB/Simulink 通信原理及仿真学习(三)
- 3. 通信信号与系统分析
- 3.1 离散信号和系统
- 3.1.1 离散信号
- 3.1.2 离散时间信号
- 3.1.3 信号的能量和功率
- 3.2 傅里叶(Fourier)分析
- 3.2.1 连续时间信号的Fourier变换
- 3.2.2 离散时间信号的Fourier变换
- 3.2.3 离散Fourier变换
MATLAB/Simulink 通信原理及仿真学习(三)
3. 通信信号与系统分析
- 数字通信的研究包括数字形式的信息从产生该信息的信源到一个或多个目的地的传输问题。
3.1 离散信号和系统
- 信号是信息的物理表现形式或说是传递信息的函数,系统定义为处理(或变换)信号的物理设备。
3.1.1 离散信号
一个信号x(t)x(t)x(t)可以是连续时间信号(模拟信号),也可以是离散时间信号(数字信号)。若x(t)x(t)x(t)是离散信号,则ttt仅在时间轴的离散点上取值,这时,应将x(t)x(t)x(t)该记为x(nTs)x(nT_s)x(nTs),TsT_sTs表示相邻两个点之间的时间间隔,又称抽样周期,nnn取整数,即
x(nTs),n=−N1,⋯,0,1,⋯,N2\begin{equation} x(nT_s),n=-N_1,\cdots,0,1,\cdots,N_2 \tag{3-1} \end{equation} x(nTs),n=−N1,⋯,0,1,⋯,N2(3-1)
式中,N1,N2N_1,N_2N1,N2是nnn的取值范围。一般可以把TsT_sTs归一化为1,则x(nTs)x(nT_s)x(nTs)可简记为x(n)x(n)x(n)。
(一直没写MATLAB,差点忘了,注释的符号是 %)
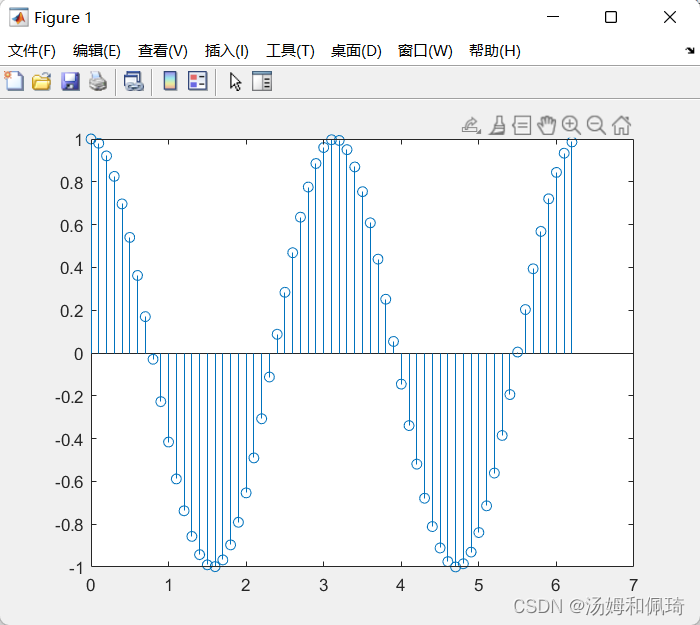
- 例一
% x=cos(2t),抽样序列为0<=t<=2*pi,抽样周期T_s=0.1.
t=0:0.1:2*pi;
x=cos(2*t);
stem(t,x);
输出结果:
1)信号的相加或相乘
{x(n)=x1(n)+x2(n)y(n)=x1(n)x2(n)\begin{cases} x(n) = x_1(n)+x_2(n)\\ y(n) = x_1(n)x_2(n) \end{cases} {x(n)=x1(n)+x2(n)y(n)=x1(n)x2(n)
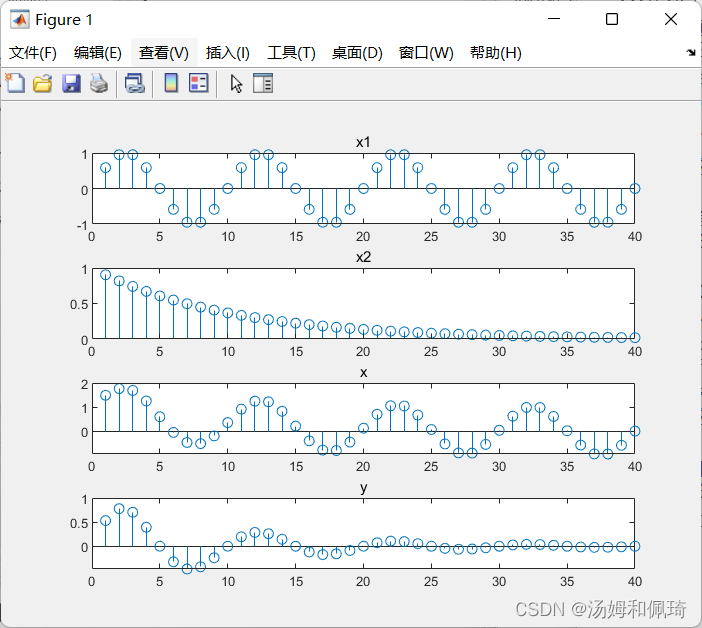
- 例二
% 信号x1(n)=sin(2*pi*0.1n)和x2(n)=exp(-0.1*n),
% 在0<=n<=40的相加和相乘序列
clear all;
n=1:40;
x1=sin(2*pi*0.1*n);
x2=exp(-0.1*n);
x=x1+x2;
y=x1.*x2;
subplot(4,1,1);stem(n,x1);title('x1');
subplot(4,1,2);stem(n,x2);title('x2');
subplot(4,1,3);stem(n,x);title('x');
subplot(4,1,4);stem(n,y);title('y');
输出结果:
2)卷积和
y(n)=∑m=−∞∞x(m)h(n−m)=x(n)∗h(n)(3-3)y(n)=\sum\limits_{m=-\infin}^{\infin}x(m)h(n-m)=x(n)*h(n)\tag{3-3} y(n)=m=−∞∑∞x(m)h(n−m)=x(n)∗h(n)(3-3)
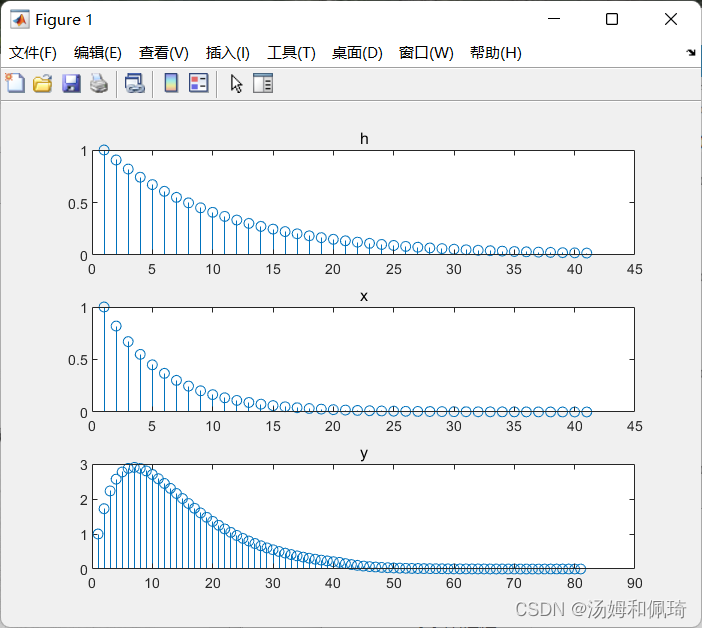
- 例三
% h(n)=exp(-0.1*n),x(n)=exp(-0.2*n),0<=n<=40的卷积和
clear all;
n=0:40;
h=exp(-0.1*n);
x=exp(-0.2*n);
y=conv(x,h);
subplot(3,1,1);stem(h);title('h');
subplot(3,1,2);stem(x);title('x');
subplot(3,1,3);stem(y);title('y');
输出结果:
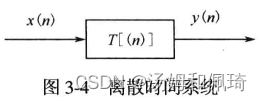
3.1.2 离散时间信号
- 离散时间系统可抽象为一种变换或一种映射,输入序列x(n)x(n)x(n)变换为输出序列y(n)y(n)y(n),即
y(n)=T[x(n)](3-4)y(n)=T[x(n)]\tag{3-4} y(n)=T[x(n)](3-4)
式中,TTT代表变换。
离散时间系统:
- 例四
一个离散时间系统的输入和输出关系为:
y(n)=ay(n−1)+x(n)(3-5)y(n)=ay(n-1)+x(n)\tag{3-5} y(n)=ay(n−1)+x(n)(3-5)
式中,a为常数。该系统表示,现在时刻的输入y(n)y(n)y(n)等于上一次的输出y(n−1)y(n-1)y(n−1)乘以常数a再加上现在的输入x(n)x(n)x(n),这是一个一阶的自回归差分方程,若
(1)x(n)={1,n=00,n≠0(2)x(n)={exp(−0.1n),0≤n≤400,其他(1) \quad x(n)= \begin{cases} 1,n=0 \\ 0,n\neq0 \end{cases}\\ (2)\quad x(n)= \begin{cases} exp(-0.1n),& 0 \le n \le 40\\ 0, & \text{其他} \end{cases} (1)x(n)={1,n=00,n=0(2)x(n)={exp(−0.1n),0,0≤n≤40其他
且a=0.8,y(n)=0,n<0,y(0)=x(0)a=0.8,y(n)=0,n<0,y(0)=x(0)a=0.8,y(n)=0,n<0,y(0)=x(0),是分别求上述系统在所给输入下的响应。
clear all
N=60;%序列长度
% 设置x1和x2
x1=zeros(1,N);
x1(1)=1;
x2=zeros(1,N);
x2(1:41)=exp(-0.1*(0:40));
% 初始状态设置
y1(1)=x1(1);
y2(1)=x2(1);
% 求取y(n)
for n=2:Ny1(n)=0.8*y1(n-1)+x1(n);y2(n)=0.8*y2(n-1)+x2(n);
end
% 绘图
subplot(4,1,1);stem(x1);title('x1');
subplot(4,1,2);stem(x2);title('x2');
subplot(4,1,3);stem(y1);title('y1');
subplot(4,1,4);stem(y2);title('y2');
输出结果

- 例五
一个离散时间系统的输入/输出关系为
y(n)=∑k=0M−1b(k)x(n−k)(3-6)y(n)=\sum\limits_{k=0}^{M-1}b(k)x(n-k)\tag{3-6} y(n)=k=0∑M−1b(k)x(n−k)(3-6)
式中,b(0),b(1),⋯,b(M−1)b(0),b(1),\cdots,b(M-1)b(0),b(1),⋯,b(M−1)为常数。
这一类系统为“有限冲激响应”系统,简称为FIR系统(上一时刻的输出对下一时刻的输出没有影响)。一阶自回归模型中由于包含了由输出到输入的反馈,因此其冲激响应为无限长,这一类系统称为“无限冲激响应”系统,简称IIR系统(包含上一时刻的输出对下一时刻输出的影响)。
在式(3-6)中,设M=3,b(0)=1/2,b(1)=1/8,b(2)=3/8,x(n)={1,0≤n≤50,其他M=3,b(0)=1/2,b(1)=1/8,b(2)=3/8,x(n)=\begin{cases}1,0 \le n \le 5 \\ 0,\text{其他} \end{cases}M=3,b(0)=1/2,b(1)=1/8,b(2)=3/8,x(n)={1,0≤n≤50,其他,试求其输出响应,
clear all
x = ones(1,6);
b = [1/2,1/8,3/8];
y=conv(x,b);
subplot(3,1,1);stem(x);title('x');
subplot(3,1,2);stem(b);title('b');
subplot(3,1,3);stem(y);title('y');
输出结果:
3.1.3 信号的能量和功率
- 能量定义:
E=∫−∞∞∣x(t)∣2dt(3-7)E = \int_{-\infin}^{\infin}|x(t)|^2 dt\tag{3-7} E=∫−∞∞∣x(t)∣2dt(3-7)
E=∑−∞∞∣x(n)∣2(3-8)E = \sum\limits_{-\infin}^{\infin}|x(n)|^2\tag{3-8} E=−∞∑∞∣x(n)∣2(3-8)
如果E<∞E < \infinE<∞,称 x(t),x(n)x(t),x(n)x(t),x(n)为能量有限信号,简称能量信号;E>∞E > \infinE>∞,则称为能量无限信号。若x(t)x(t)x(t)和x(n)x(n)x(n)能量无限,往往开展其功率的研究,即
P=limT→∞1T∫−T/2T/2∣x(t)∣2dt(3-9)P=\lim\limits_{T \to \infin}\frac{1}{T}\int_{-T/2}^{T/2}|x(t)|^2dt\tag{3-9} P=T→∞limT1∫−T/2T/2∣x(t)∣2dt(3-9)
P=limN→∞12N+1∑n=−NN∣x(n)∣2(3-10)P=\lim\limits_{N \to \infin}\frac{1}{2N+1}\sum\limits_{n=-N}^{N}|x(n)|^2\tag{3-10} P=N→∞lim2N+11n=−N∑N∣x(n)∣2(3-10)
若P<∞P < \infinP<∞,则称x(t),x(n)x(t),x(n)x(t),x(n)为功率有限信号,简称功率信号。
- 周期信号、准周期信号与随机信号,由于其时间是无限的,因而为功率信号。一般在有限区间内存在的确定信号是能量信号。例如:x(n)=1,1≤n≤100x(n)=1,1 \le n \le 100x(n)=1,1≤n≤100是能量信号,x(n)=sin(2πn),−∞≤n≤∞x(n)=sin(2\pi n),-\infin \le n \le \infinx(n)=sin(2πn),−∞≤n≤∞是功率信号。
3.2 傅里叶(Fourier)分析
连续时间信号的Fourier变换和Fourier级数,数字信号处理中的离散Fourier变换(DFT)。
3.2.1 连续时间信号的Fourier变换
设x(t)x(t)x(t)为以连续时间信号,若x(t)x(t)x(t)绝对可积,即
∫−∞∞∣x(t)∣dt<∞(3-11)\int_{-\infin}^{\infin}|x(t)|dt<\infin\tag{3-11} ∫−∞∞∣x(t)∣dt<∞(3-11)
那么,x(t)x(t)x(t)的Fourier变换存在,并定义为:
X(jΩ)=∫−∞∞x(t)e−jΩtdt(3-12)X(j\Omega)=\int_{-\infin}^{\infin}x(t)e^{-j \Omega t}dt\tag{3-12} X(jΩ)=∫−∞∞x(t)e−jΩtdt(3-12)
其反变换为:
x(t)=12π∫−∞∞X(jΩ)ejΩtdΩ(3-13)x(t)=\frac{1}{2\pi}\int_{-\infin}^{\infin}X(j\Omega)e^{j \Omega t}d \Omega\tag{3-13} x(t)=2π1∫−∞∞X(jΩ)ejΩtdΩ(3-13)
式中,Ω=2πf\Omega=2 \pi fΩ=2πf,单位为rad/s,将X(jΩ)X(j\Omega)X(jΩ)表示成∣X(jΩ)∣ejφ(Ω)|X(j\Omega)|e^{j\varphi(\Omega)}∣X(jΩ)∣ejφ(Ω)的形式,即可得到∣X(jΩ)∣|X(j\Omega)|∣X(jΩ)∣和φ(Ω)\varphi(\Omega)φ(Ω)随 变化的曲线,分别成为幅频特性和相频特性。
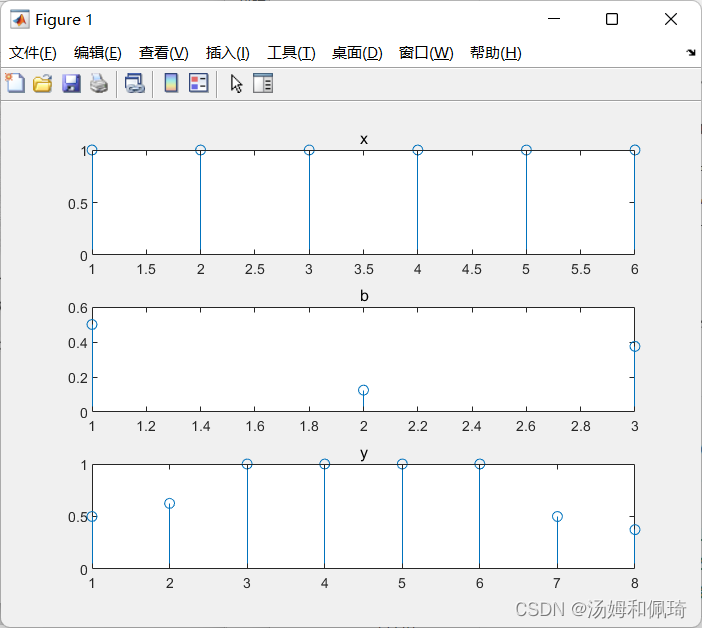
- 例六
绘制f(t)=te−∣t∣f(t)=te^{-|t|}f(t)=te−∣t∣的时域波形及傅里叶变化后的幅频特性。
clear all
% 定义符号变量t
syms t;
f = t*exp(-abs(t));
F = fourier(f)
% 绘制函数曲线
subplot(1,2,1);ezplot(f);
subplot(1,2,2);ezplot(abs(F));

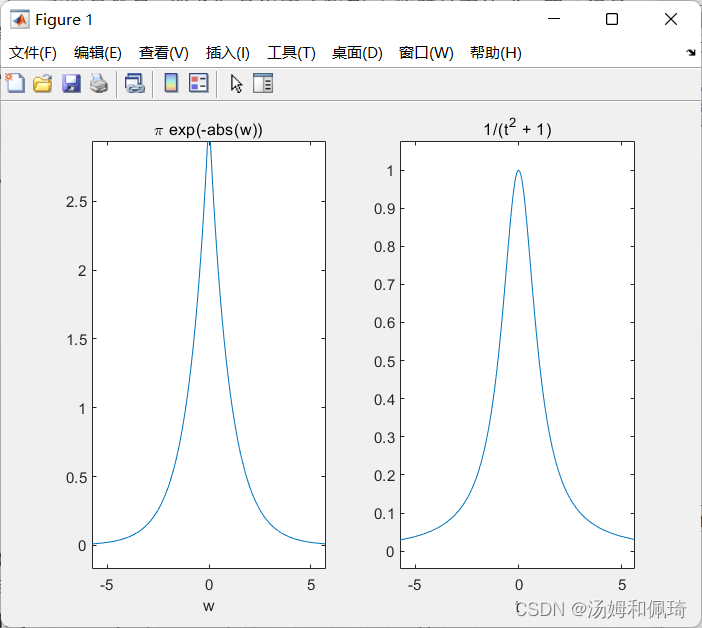
- 例七
某信号的Fourier变换F(ω)=πe−∣ω∣F(\omega)=\pi e^{-|\omega|}F(ω)=πe−∣ω∣,试绘制该信号的时域波形和幅频特性。
clear all
syms t w;
F = pi*exp(-abs(w));
f = ifourier(F,t);
subplot(1,2,1);ezplot(abs(F));
subplot(1,2,2);ezplot(f);
-
严格而将只有非周期函数才有Fourier变换,但若x(t)x(t)x(t)是周期函数,即 ,此时不满足(3-11)的绝对可积条件,此时要求x(t)x(t)x(t)满足狄利克雷条件(Dirichlet),即:(1 )在一周期内,连续或只有有限个第一类间断点(该点含有左右极限);(2)在一周期内,极大值和极小值的数目应是有限个;(3)在一周期内,信号是绝对可积的。
-
Fourier级数为:
x(t)=∑k=−∞∞X(kΩ0)ejkΩ0t,k=0,±1,⋯,±∞(3-14)x(t)=\sum\limits_{k=-\infin}^{\infin}X(k\Omega_0)e^{jk \Omega_0 t},k=0,\pm1,\cdots,\pm\infin\tag{3-14} x(t)=k=−∞∑∞X(kΩ0)ejkΩ0t,k=0,±1,⋯,±∞(3-14)
其中Ω0=2π/T0=2πf0\Omega_0=2\pi/T_0=2\pi f_0Ω0=2π/T0=2πf0,为信号x(t)x(t)x(t)的基波频率,kΩ0k\Omega_0kΩ0为其第k次谐波频率:X(kΩ0)X(k\Omega_0)X(kΩ0)称为x(t)x(t)x(t)在k次谐波处的Fourier系数,它的幅度反映了信号x(t)x(t)x(t)中所包含的频率为kΩ0k\Omega_0kΩ0的成分大小。 -
可以看出周期信号x(t)x(t)x(t)可以由无数个复正弦[ejkΩ0t,k=0,±1,⋯,±∞][e^{jk\Omega_0 t},k=0,\pm 1,\cdots,\pm\infin][ejkΩ0t,k=0,±1,⋯,±∞] 作为基本信号再乘以不同的加权值X(kΩ0)X(k\Omega_0)X(kΩ0)复合而成。X(kΩ0)X(k\Omega_0)X(kΩ0)仅在Ω0\Omega_0Ω0的整数倍上取值,所以其在频率轴上取离散值, 即:
X(kΩ0)=1T∫tt+Tx(t)e−jkΩ0tdt(3-15)X(k\Omega_0)=\frac{1}{T}\int_{t}^{t+T}x(t)e^{-jk \Omega_0 t}dt\tag{3-15} X(kΩ0)=T1∫tt+Tx(t)e−jkΩ0tdt(3-15)
其中X(kΩ0)X(k\Omega_0)X(kΩ0)是复数,所以
X(kΩ0)=∣X(kΩ0)∣ejθkX(k\Omega_0)=|X(k\Omega_0)|e^{j\theta_k} X(kΩ0)=∣X(kΩ0)∣ejθk
式中,∣X(kΩ0)∣|X(k\Omega_0)|∣X(kΩ0)∣是频率为nf0nf_0nf0的分量的振幅,θk\theta_kθk是频率是nf0nf_0nf0的分量的相位。 -
注意X(kΩ0)X(k\Omega_0)X(kΩ0)和X(jΩ)X(j\Omega)X(jΩ)的物理意义不同,前者是Ω\OmegaΩ轴上的离散函数,后者则是Ω\OmegaΩ轴上的连续函数,同时前者是谐波幅度,后者是频谱密度。
-
例八(Ω0=2π/T\Omega_0 = 2\pi/TΩ0=2π/T)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ezyTS3QQ-1677072960929)(../../AppData/Roaming/Typora/typora-user-images/image-20230221191357027.png)]](https://img-blog.csdnimg.cn/48544c2f101c4d8bac215c074d858de4.png)
clear all
k=-50:50;
X=0.25*sinc(k/4);
stem(k,X)
3.2.2 离散时间信号的Fourier变换
-
设h(n)h(n)h(n)为一线形时不变系统的单位抽样响应,定义
H(ejω)=∑n=−∞∞h(n)e−jωn(3-20)H(e^{j\omega})=\sum\limits_{n=-\infin}^{\infin}h(n)e^{-j\omega n}\tag{3-20} H(ejω)=n=−∞∑∞h(n)e−jωn(3-20)
为系统的频率响应,记住了这是离散时间序列的Fourier变换(Discrete Time Fourier Transform, DTFT)。H(ejω)H(e^{j\omega})H(ejω)是ω\omegaω的连续函数,周期为2π2\pi2π 。其中ω\omegaω为数字频率。(3-20)的DTFT是周期信号H(ejω)H(e^{j\omega})H(ejω)在频域内展开成的Fourier级数,其Fourier系数是时域信号h(n)h(n)h(n)。 -
离散信号h(n)h(n)h(n)的DTFT存在的条件是h(n)h(n)h(n)是绝对可和的,既满足:
∑n=−∞∞∣h(n)∣<∞(3-21)\sum\limits_{n=-\infin}^{\infin} |h(n)| < \infin\tag{3-21} n=−∞∑∞∣h(n)∣<∞(3-21) -
相应的,其DTFT反变换(IDTFT)可以表示为:
h(n)=12π∫−ππH(ejω)ejωndω(3-22)h(n)=\frac{1}{2\pi}\int_{-\pi}^{\pi}H(e^{j\omega})e^{j\omega n}d\omega\tag{3-22} h(n)=2π1∫−ππH(ejω)ejωndω(3-22)
根据上述DTFT的定义,可以利用MATLAB,由h(n)h(n)h(n)直接计算H(ejω)H(e^{j\omega})H(ejω)在频率区间 [0,π][0,\pi][0,π]的值并绘制对应的模和相角。 -
假设序列h(n)h(n)h(n)在区间n1≤n≤n2n_1 \le n \le n_2n1≤n≤n2有NNN个样本值,要计算其在下述频率点上的H(ejω)H(e^{j\omega})H(ejω) :
ϖk=kπM,k=0,1,⋯,M−1(3-23)\varpi_k = k\frac{\pi}{M},k=0,1,\cdots,M-1\tag{3-23} ϖk=kMπ,k=0,1,⋯,M−1(3-23)
首先定义一个(M+1)×N(M+1) \times N(M+1)×N 的矩阵,即
W=W(k,n)=e−j(πM)kn,n1≤n≤n2,k=0,1,⋯,M−1(3-24)\boldsymbol W={W(k,n)=e^{-j(\frac{\pi}{M})kn},n_1 \le n \le n_2,k=0,1,\cdots,M-1}\tag{3-24} W=W(k,n)=e−j(Mπ)kn,n1≤n≤n2,k=0,1,⋯,M−1(3-24)
如果将{k}\{k\}{k}和{n}\{n\}{n}写为列矢量,则有
W=[e−j(π/M)KTn](3-25)\boldsymbol W=[e^{-j(\pi/M)K^Tn}]\tag{3-25} W=[e−j(π/M)KTn](3-25)
于是,在所求频率点上的H(ejω)H(e^{j\omega})H(ejω)值可以写为:
HT=hT∗W(3-26)H^T=h^T*\boldsymbol W\tag{3-26} HT=hT∗W(3-26) -
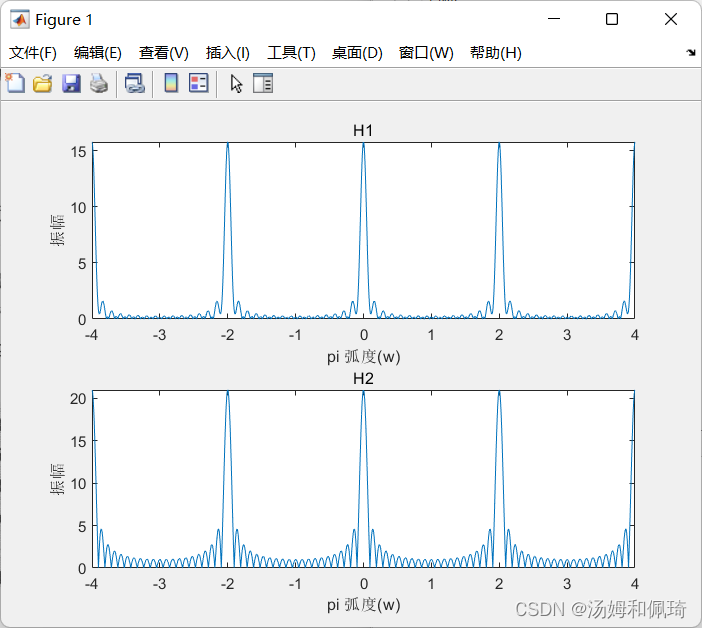
例九

w = -4:0.001:4;
n1=-15:15;
n2=0:20;
h1=exp(-abs(0.1*n1));
h2(n2+1)=1;
Hjw1=h1*(exp(-j*pi).^(n1'*w));
Hjw2=h2*(exp(-j*pi).^(n2'*w));
subplot(2,1,1);plot(w,abs(Hjw1));
title('H1');xlabel('pi 弧度(w)');ylabel('振幅');
subplot(2,1,2);plot(w,abs(Hjw2));
title('H2');xlabel('pi 弧度(w)');ylabel('振幅');
离散时间信号的Fourier变换的性质十分重要,如卷积性质、频移性质等。
DTFT的频移性质是指,序列乘以复指数序列对应于频域的频移,即
DTFT(h(n)ejω1n)=H(ej(ω−ω1))(3-27)DTFT(h(n)e^{j\omega_1 n})=H(e^{j(\omega-\omega_1)})\tag{3-27} DTFT(h(n)ejω1n)=H(ej(ω−ω1))(3-27)
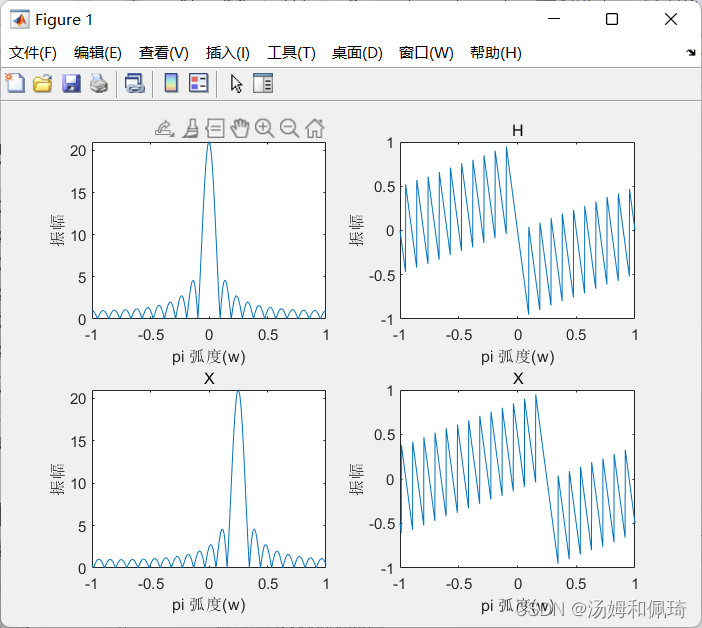
- 例十
给定序列h(n)=1,0len≤20h(n)=1,0 \ le n \le 20h(n)=1,0 len≤20 和 x(n)=h(n)ejπn/4x(n)=h(n)e^{j\pi n/4}x(n)=h(n)ejπn/4,分别计算它们的离散时间Fourier,并比较结果。
clear all
w=-1:0.001:1;
n=0:20;
h(n+1)=1;
x=h.*exp(j*pi*n/4);
Hjw=h*(exp(-j*pi).^(n'*w));
Xjw=x*(exp(-j*pi).^(n'*w));
subplot(2,2,1);plot(w,abs(Hjw));
title('H');xlabel('pi 弧度(w)');ylabel('振幅');
subplot(2,2,2);plot(w,angle(Hjw)/pi);
title('H');xlabel('pi 弧度(w)');ylabel('振幅');
subplot(2,2,3);plot(w,abs(Xjw));
title('X');xlabel('pi 弧度(w)');ylabel('振幅');
subplot(2,2,4);plot(w,angle(Xjw)/pi);
title('X');xlabel('pi 弧度(w)');ylabel('振幅');
一个单位脉冲响应为h(n)h(n)h(n)的系统对输入序列x(n)x(n)x(n)的输出为:
y(n)=x(n)∗h(n)(3-28)y(n)=x(n)*h(n)\tag{3-28} y(n)=x(n)∗h(n)(3-28)
根据DTFT的卷积性质,有:
Y(ejω)=DTFT[y(n)]=DTFT[x(n)∗h(n)]=X(ejω)H(ejω)(3-29)Y(e^{j\omega})=DTFT[y(n)]=DTFT[x(n)*h(n)]=X(e^{j\omega})H(e^{j\omega})\tag{3-29} Y(ejω)=DTFT[y(n)]=DTFT[x(n)∗h(n)]=X(ejω)H(ejω)(3-29)
可以利用这一性质求系统在输入信号为x(n)x(n)x(n)时的系统响应。可以先求出X(ejω)X(e^{j\omega})X(ejω)和H(ejω)H(e^{j\omega})H(ejω),进而求出Y(ejω)Y(e^{j\omega})Y(ejω),再通过IDTFT求出y(n)y(n)y(n),绕过求卷积的步骤。
- 例11 一个系统的单位脉冲响应h(n)=sin(0.2n)e−0.1n,0≤n≤30h(n)=sin(0.2n)e^{-0.1n},0 \le n \le 30h(n)=sin(0.2n)e−0.1n,0≤n≤30,试求:
(1)该系统的频率响应;
(2)若输入信号为x(n)=2sin(0.2πn)+3cos(0.4πn),0≤n≤30x(n)=2sin(0.2\pi n)+3cos(0.4\pi n),0 \le n \le 30x(n)=2sin(0.2πn)+3cos(0.4πn),0≤n≤30,确定该系统的稳态输出。
clear all
w=-1:0.001:1;
n=0:30;
h=sinc(0.2*n);
x=2*sin(0.2*pi*n)+3*cos(0.4*pi*n);
Hjw=h*exp(-j*pi).^(n'*w);
Xjw=x*exp(-j*pi).^(n'*w);
Yjw=Xjw.*Hjw;
n1=0:2*length(n)-2;
dw=0.001*pi;
y=(dw*Yjw*(exp(j*pi).^(w'*n1)))/(2*pi);
y1=conv(x,h);
subplot(3,1,1);plot(w,abs(Hjw))
title('H');xlabel('pi 弧度(w)');ylabel('振幅');
subplot(3,1,2);plot(w,abs(Xjw))
title('X');xlabel('pi 弧度(w)');ylabel('振幅');
subplot(3,1,3);plot(w,abs(Yjw))
title('Y');xlabel('pi 弧度(w)');ylabel('振幅');


3.2.3 离散Fourier变换
- 3.2.2节学习的DTFT的特点是:(1)变换使用无限长的序列;(2)变换的结果是自变量ω\omegaω的连续函数。(时域上连续,在计算机的使用上很难实现。)因而需要一种时域和频域上都离散的计算方法,这便是离散Fourier变换(DFT),也成为快速Fourier变换(FFT)。
- 给定一个离散序列x(n)x(n)x(n),其DFT和IDFT如下:
{X(k)=∑n=0N−1x(n)e−j2πnnk=∑n=0N−1x(n)WNnk,k=0,1,⋯,N−1x(n)=1N∑n=0N−1X(k)ej2πnnk=1N∑n=0N−1x(n)WN−nk,n=0,1,⋯,N−1(3-30)\begin{cases} X(k)=\sum\limits_{n=0}^{N-1}x(n)e^{-j\frac{2\pi}{n}nk}=\sum\limits_{n=0}^{N-1}x(n)W_N^{nk},k=0,1,\cdots,N-1 \\ x(n)=\frac{1}{N}\sum\limits_{n=0}^{N-1}X(k)e^{j\frac{2\pi}{n}nk}=\frac{1}{N}\sum\limits_{n=0}^{N-1}x(n)W_N^{-nk},n=0,1,\cdots,N-1\tag{3-30} \end{cases} ⎩⎨⎧X(k)=n=0∑N−1x(n)e−jn2πnk=n=0∑N−1x(n)WNnk,k=0,1,⋯,N−1x(n)=N1n=0∑N−1X(k)ejn2πnk=N1n=0∑N−1x(n)WN−nk,n=0,1,⋯,N−1(3-30)
式中,WN=e−j2πNW_N=e^{-j\frac{2\pi}{N}}WN=e−jN2π。DFT对应的是时域和频域都是有限长,且都是离散的。
- 例十二 离散序列x(n)=sin(0.2n)e−0.1n,0≤n≤30x(n)=sin(0.2n)e^{-0.1n},0 \le n \le 30x(n)=sin(0.2n)e−0.1n,0≤n≤30,试求该序列的DFT。
clear all
n=0:30;
x=sin(0.2*n).*exp(-0.1*n);
k=-0:30;
N=31;
Wnk=exp(-j*2*pi/N).^(n'*k);
X=x*Wnk;
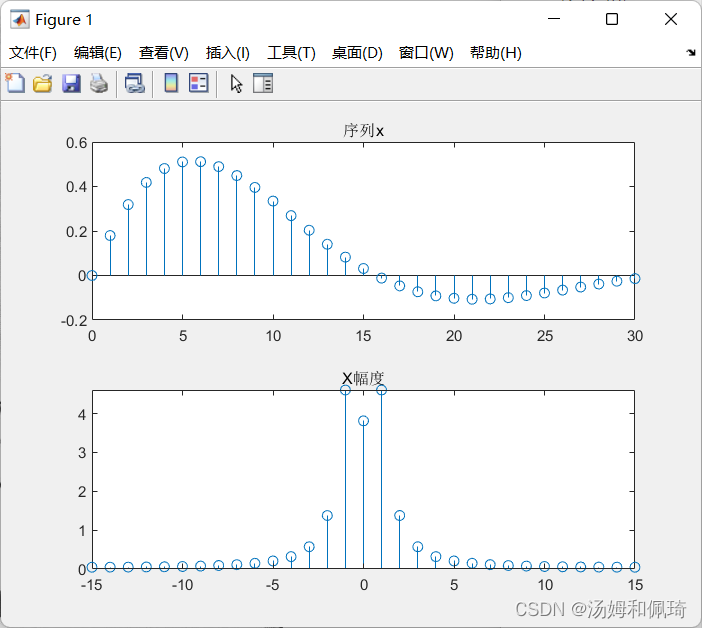
subplot(2,1,1);stem(n,x);title('序列x');
% DFT默认的下标范围是[0,N-1],采取对下标的重新排列,
% 体现序列DFT的对称性
subplot(2,1,2);stem(-15:15, [abs(X(17:end)) abs(X(1:16))]);title('X幅度');
输出结果
- MATLAB提供fft函数计算优先离散序列的DFT,DFT的循环卷积性质,可以设序列x(n),h(n)x(n),h(n)x(n),h(n)都是N点序列,其DFT分别是X(k),H(k),Y(k)X(k),H(k),Y(k)X(k),H(k),Y(k),若

则
Y(k)=X(k)H(k)(3-32)Y(k)=X(k)H(k)\tag{3-32} Y(k)=X(k)H(k)(3-32)
式中圈中间一个N的符号表示做N点循环卷积。
- 一般对两个N点序列的循环卷积,其矩阵形式如下:
y=[y(0)y(1)⋮y(N−1)]=[h(0)h(N−1)⋯h(1)h(1)h(0)⋯h(2)⋮⋮⋮h(N−1)h(N−2)⋯h(2)]⋅[x(0)x(1)⋮x(N−1)]=H⋅x(3-33)y=\begin{bmatrix}y(0)\\y(1)\\ \vdots\\y(N-1)\end{bmatrix}=\begin{bmatrix}&h(0) &h(N-1) &\cdots h(1)\\&h(1) &h(0) &\cdots h(2)\\ &\vdots &\vdots &\vdots\\&h(N-1) &h(N-2) &\cdots h(2)\\ \end{bmatrix} \cdot \begin{bmatrix}x(0)\\x(1)\\ \vdots\\x(N-1)\end{bmatrix}=\boldsymbol {H \cdot x}\tag{3-33} y=y(0)y(1)⋮y(N−1)=h(0)h(1)⋮h(N−1)h(N−1)h(0)⋮h(N−2)⋯h(1)⋯h(2)⋮⋯h(2)⋅x(0)x(1)⋮x(N−1)=H⋅x(3-33)
式(3-33)中矩阵HHH成为循环矩阵,由第1行开始,依次向右移动一个元素,移出去的元素在下一行的最左边出现,即每一行都是由h(0),h(N−1),⋯,h(1)h(0),h(N-1),\cdots,h(1)h(0),h(N−1),⋯,h(1)这N个元素依此法则移动所生成的,故成为HHH为循环矩阵,因此对应的卷积为循环卷积。
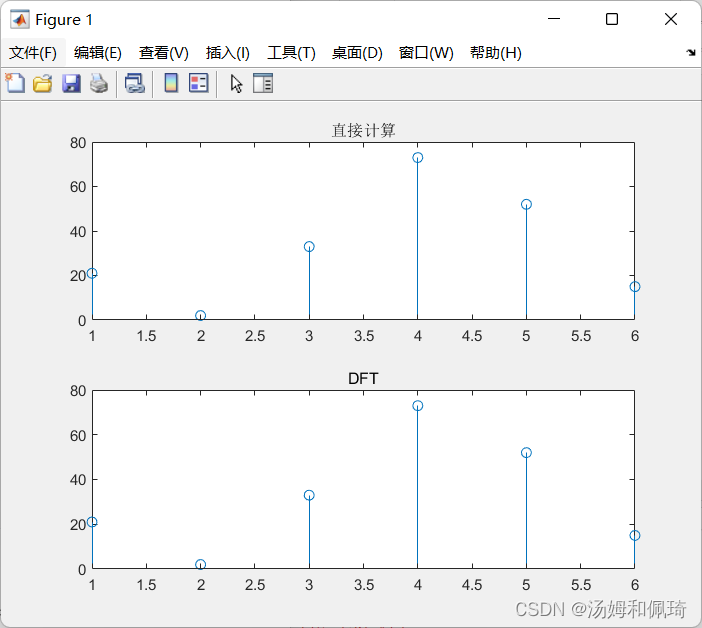
- 例十三
已知序列h(n)=6,3,4,2,1,−2,x(n)=3,2,6,7,−1,−3)h(n)={6,3,4,2,1,-2},x(n)={3,2,6,7,-1,-3})h(n)=6,3,4,2,1,−2,x(n)=3,2,6,7,−1,−3),试分别用直接法和DFT,求两个序列的循环卷积序列。
% examp-13
clear all
h = [6 3 4 2 1 -2];
x = [3 2 6 7 -1 -3];
% 反转序列h
h1=fliplr(h);
% 利用toeolitz生成循环矩阵
H=toeplitz(h,[h(1) h1(1:5)]);
y=H*x';H=fft(h);
X=fft(x);
Y=H.*X;
y1=ifft(Y);subplot(2,1,1);stem(y);title('直接计算')
subplot(2,1,2);stem(y1);title('DFT')
输出结果:
- 设x(n)x(n)x(n)为一MMM点序列,h(n)h(n)h(n)为一LLL点序列,y(n)=x(n)∗h(n)y(n)=x(n)*h(n)y(n)=x(n)∗h(n),即y(n)y(n)y(n)是x(n)x(n)x(n)和h(n)h(n)h(n)的线性卷积,那么y(n)y(n)y(n)是一(M+L−1)(M+L-1)(M+L−1)点的序列。由上面的讨论可知,DFT对应循环卷积而不对应线性卷积。如果利用DFT计算两个序列的线性卷积,则可以采用以下方法:

-
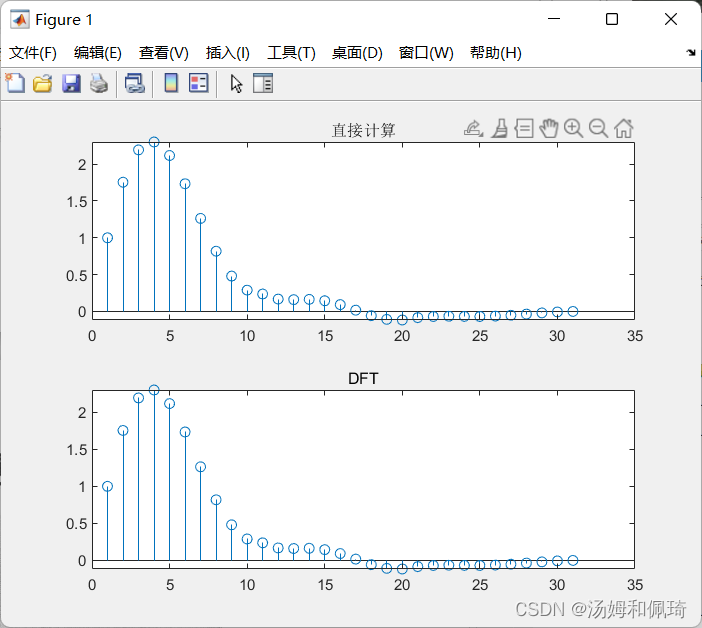
例十四
已知序列h(n)=sinc(0.2n),0≤n≤20,x(n)=e−0.2n,0≤n≤10h(n)=sinc(0.2n),0 \le n \le 20,x(n)=e^{-0.2n},0 \le n \le 10h(n)=sinc(0.2n),0≤n≤20,x(n)=e−0.2n,0≤n≤10,试分别用直接法和DFT法求两个序列的线性卷积序列。
%exmap-14 clear all n1=0:20; n2=0:10; h=sinc(0.2*n1); x=exp(-0.2*n2); y=conv(x,h);% 补齐M+L-1的长度 h1=[h zeros(1,length(x)-1)]; x1=[x zeros(1,length(h)-1)]; H1=fft(h1); X1=fft(x1); Y1=H1.*X1; y1=ifft(Y1);subplot(2,1,1);stem(y);title('直接计算'); subplot(2,1,2);stem(y1);title('DFT');
输出结果
相关文章:

MATLAB/Simulink 通信原理及仿真学习(三)
文章目录MATLAB/Simulink 通信原理及仿真学习(三)3. 通信信号与系统分析3.1 离散信号和系统3.1.1 离散信号3.1.2 离散时间信号3.1.3 信号的能量和功率3.2 傅里叶(Fourier)分析3.2.1 连续时间信号的Fourier变换3.2.2 离散时间信号的…...
如何解决过拟合与欠拟合,及理解k折交叉验证
模型欠拟合:在训练集以及测试集上同时具有较⾼的误差,此时模型的偏差较⼤; 模型过拟合:在训练集上具有较低的误差,在测试集上具有较⾼的误差,此时模型的⽅差较⼤。 如何解决⽋拟合: 添加其他特…...
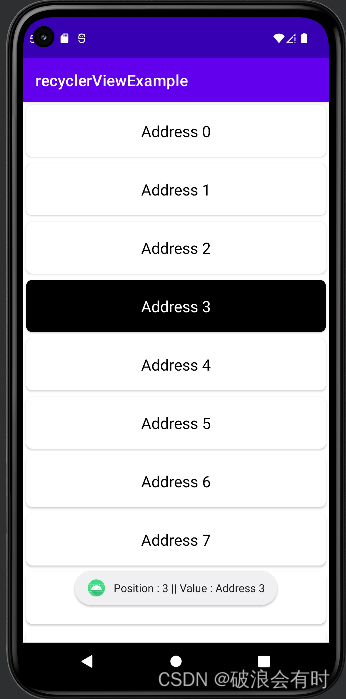
Kotlin 34. recyclerView 案例:显示列表
Kotlin 案例1. recyclerView:显示列表 这里,我们将通过几个案例来介绍如何使用recyclerView。RecyclerView 是 ListView 的高级版本。 当我们有很长的项目列表需要显示的时候,我们就可以使用 RecyclerView。 它具有重用其视图的能力。 在 Re…...

JAVA练习58-汉明距离、颠倒二进制位
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目1-汉明距离 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 二、题目2-颠倒二进制位 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总结 前言 提示…...

优炫数据库百城巡展,成都首站圆满举行
2月17日,由四川省大数据发展研究会、北京优炫软件股份有限公司联合举办的“首届四川省推进信息技术应用创新产业服务研讨会暨优炫数据库百城巡展成都首站隆重举行。此次活动是优炫数据库百城巡展的起点站,更是国产数据库市场美好乐章的一次强力鸣奏。 来…...

【20230210】二叉树小结
二叉树的种类二叉树的主要形式:满二叉树和完全二叉树。满二叉树深度为k,有2^k-1个节点的二叉树完全二叉树除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。二叉搜索树…...
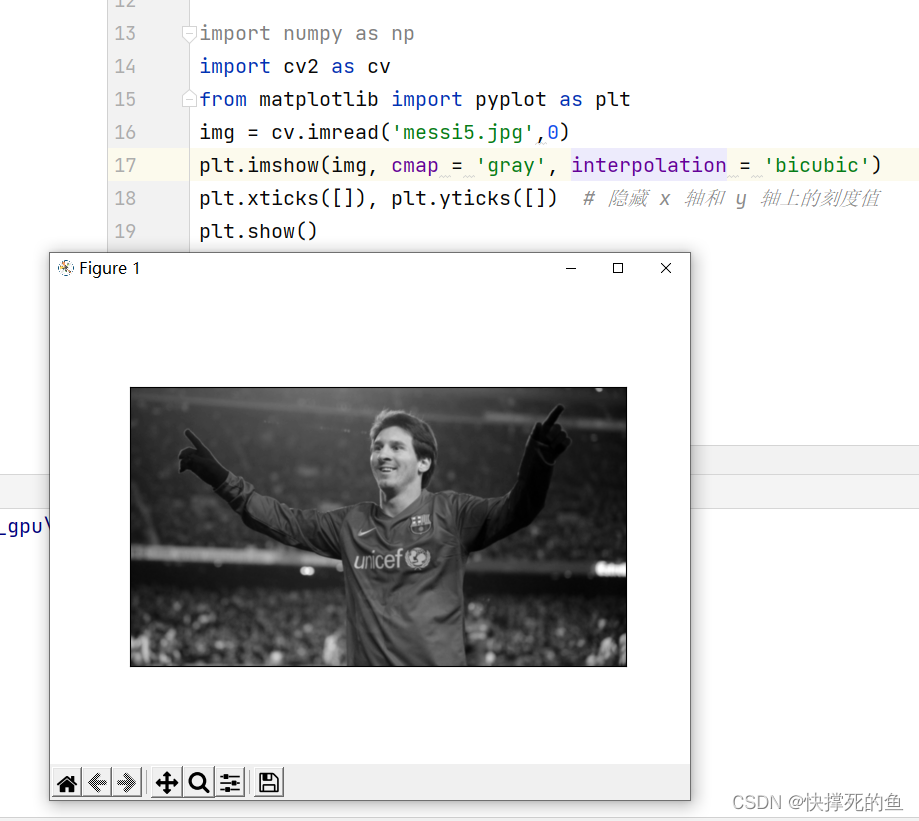
openCV—图像入门(python)
目录 目标 使用OpenCV 显示图像 写入图像 总结使用 使用Matplotlib 注:图片后续补充 目标 在这里,你将了解如何使用Python编程语言中的OpenCV库,实现读取、显示和保存图像的功能。具体来说,你将学习以下函数的用法…...
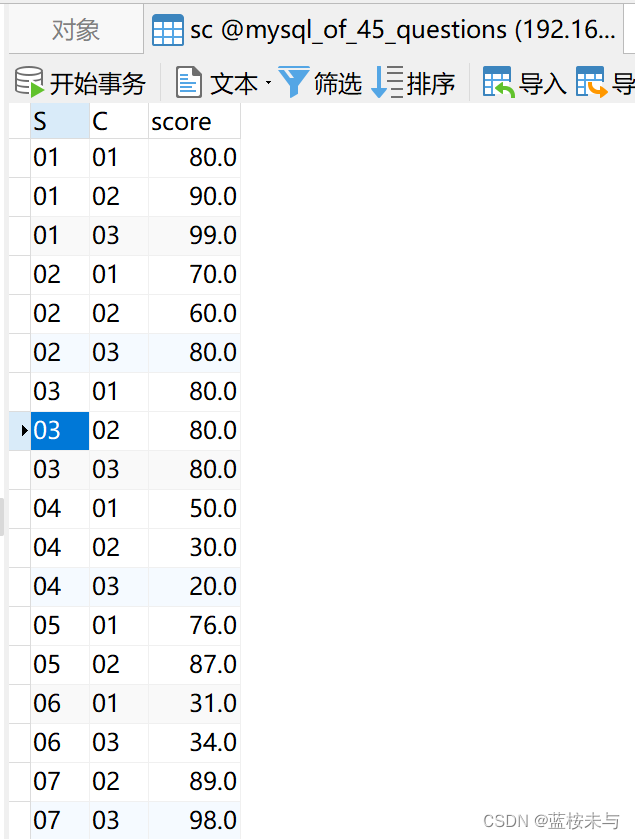
关于一个Java程序员马上要笔试了,临时抱佛脚,一晚上恶补45道简单SQL题,希望笔试能通过
MySQL随手练 / DQL篇 MySQL随手练——DQL篇 题目网盘下载:https://pan.baidu.com/s/1Ky-RJRNyfvlEJldNL_yQEQ?pwdlana 初始数据 表 course 表 student 表 teacher 表 sc 答案 :) —> :( —> :) 1. 查询 "01"课程比"02"课程成绩高的学生…...

PyTorch深度学习实战
本专栏分为两大部分,专栏内容如下: 第1部分 探讨PyTorch与其他深度学习框架的区别。 如何在PyTorch Hub中下载和运行模型。 PyTorch的基本构建组件——张量 展示不同类型的数据如何被表示为张量,以及深度学习模型期望构造什么样的张量。 梯度…...
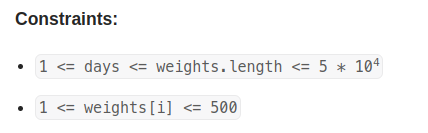
leetcode 1011. Capacity To Ship Packages Within D Days(D天内运送包裹的容量)
数组的每个元素代表每个货物的重量,注意这个货物是有先后顺序的,先来的要先运输,所以不能改变这些元素的顺序。 要days天内把这些货物全部运输出去,问所需船的最小载重量。 思路: 数组内数字顺序不能变,就…...

支持向量机SVM详细原理,Libsvm工具箱详解,svm参数说明,svm应用实例,神经网络1000案例之15
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 SVM应用实例,基于SVM的股票价格预测 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)是一种二分类模型&a…...
Mac 上搭建 iOS WebDriverAgent 环境
文章目录Mac环境搭建配置 Xcode 生成 WDA常见问题brew 安装失败Mac环境搭建 macOS 系统电脑:12.6.2 Xcode:14.0.1(xcodebuild -version) appium Desktop:1.21.0 (下载链接) Appium Desktop 1.22.0 ,从该版…...

python学习笔记之例题篇NO.3
获得用户输入的一个整数N,输出N中所出现不同数字的和。 s list(set(list(input())))# ① r…...
【Kubernetes】第七篇 - Service 服务介绍和使用
一,前言 上一篇,通过配置一个 Deployment 对象,在内部创建副本集对象,副本集帮我们创建了 3 个 pod 副本 由于 pod 存在 IP 漂移现象,pod 的创建和重启会导致 IP 变化; 本篇,介绍 Service 服…...
Linux 终端复用器Tmux
目录 Tmux讲解 配置tmux 配置tmux会话 配置tmux窗口(在会话界面进行配置) 配置tmux面板 配置窗口共享同步 Tmux讲解 RHEL5/6/7使用的是screen软件包 RHEL8使用的是tumx软件包(功能更强大,更易用) tmux的三个基本…...

Hadoop集群模式安装(Cluster mode)
1、Hadoop源码编译 安装包、源码包下载地址 Index of /dist/hadoop/common/hadoop-3.3.0为什么要重新编译Hadoop源码? 匹配不同操作系统本地库环境,Hadoop某些操作比如压缩、IO需要调用系统本地库(*.so|*.dll) 修改源码、重构源码 如何…...
PTA L1-054 福到了(详解)
前言:内容包括:题目,代码实现,大致思路,代码解读 题目: “福”字倒着贴,寓意“福到”。不论到底算不算民俗,本题且请你编写程序,把各种汉字倒过来输出。这里要处理的每…...

python -- 魔术方法
魔术方法就算定义在类里面的一些特殊的方法 特点:这些func的名字前面都有两个下划线 __new__方法 相当于一个类的创建一个对象的过程 __init__方法 相当于为这个类创建好的对象分配地址初始化的过程 __del__方法 一个类声明这个方法后,创建的对象如果…...

「JVM 编译优化」提前编译器
1996 年 JDK 1.0 发布,同年 7 月 外挂即时编译器发布(JDK 1.0.2),而 Java 提前编译发布在之后几个月(IBM High Performance Compiler for Java),1998 年 GNU 组织公布 GCC 家族新成员 GNU Compi…...

Golang channel 用法与实现原理
文章目录1.简介2.用法3.三种状态4.实现原理数据结构原理概述5.小结参考文献1.简介 Golang channel 是一种并发原语,用于在不同 goroutine 之间进行通信和同步。本质上,channel 是一种类型安全的 FIFO 队列,它可以实现多个 goroutine 之间的同…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
