如何在windows环境下编译T
一， 安装MYSYS2
1. 去https://www.msys2.org下载 msys2-x86_64-xxxxx.exe;
2. 按照msys2.org主页提示的步骤安装;
3.安装完默认起来的是 UCRT的， 可以根据环境的需要选择， 我选择的 MSYS2 MINGW64
4. 搭建编译环境， 安装对应的软件包
4.1 更新包数据和核心数据包
pacman -Syu
4.2 安装工具链
pacman -S mingw-w64-x86_64-gcc
4.3 安装其他软件和工具
pacman -S base-devel
pacman -S git
4.4 测试是否征程
gcc -v
4.5 安装cmake
pacman -S mingw-w64-x86_64-cmake mingw-w64-x86_64-extra-cmake-modules
5. 编译TR31 with the code in github
#Windows
rm -Rf build &&
cmake -B build -DCMAKE_OSX_ARCHITECTURES="x86_64;arm64" -DCMAKE_BUILD_TYPE="RelWithDebInfo" -DFETCH_MBEDTLS=YES -DFETCH_ARGP=YES &&
cmake --build build
6. 验证结果
结果OK！
$ ./tr31-tool --import B0128B1TX00N0300KS18FFFF00A0200001E00000KC0C000169E3KP0C00ECAD626F9F1A826814AA066D86C8C18BD0E14033E1EBEC75BEDF586E6E325F3AA8C0E5 --kbpk AB2E09DB3EF0BA71E0CE6CD755C23A3B
Key block format version: B
Key block length: 128 bytes
Key usage: [B1] Initial DUKPT Key (IK/IPEK)
Key algorithm: [T] TDES
Key mode of use: [X] Key Derivation
Key version: Unused
Key exportability: [N] Not exportable
Optional blocks [3]:
[KS] Initial Key Serial Number (KSN): FFFF00A0200001E00000
[KC] Key Check Value (KCV) of wrapped key: 0169E3 (Legacy KCV algorithm)
[KP] Key Check Value (KCV) of KBPK: ECAD62 (Legacy KCV algorithm)
Key length: 16
Key value: BF82DAC6A33DF92CE66E15B70E5DCEB6 (KCV: 0169E3)
二：补充：
Get submodule with git command from some project with submoudles
git -clone --recursive <project URL >
三：Reference:
1.https://www.msys2.org/
相关文章：
如何在windows环境下编译T
一， 安装MYSYS2 1. 去https://www.msys2.org下载 msys2-x86_64-xxxxx.exe; 2. 按照msys2.org主页提示的步骤安装; 3.安装完默认起来的是 UCRT的， 可以根据环境的需要选择， 我选择的 MSYS2 MINGW64 4. 搭建编译环境， 安装对应的软…...
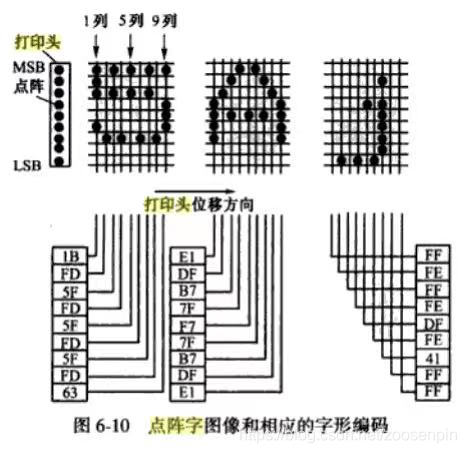
USB接口针式打印机
1 针式打印机原理 - 针式打印机16针是纵向排列，每次打印垂直的16bit，然后右移一bit，继续下列打印；字节的MSB表示最上面的点，字节LSB表示最下面的点 - 由于汉字字模的点阵是横向排列的，而提供给打印头的信息…...
外贸建站教程步骤有哪些？独立站怎么搭建？
推荐的外贸建站教程？制作国际贸易网站的流程？ 对于那些希望将产品或服务推向全球市场的企业来说，建立一个专业、具有吸引力的网站是至关重要的。下面115SHOP将介绍外贸建站教程的关键步骤，帮助您更好地了解如何在国际市场上建立您…...
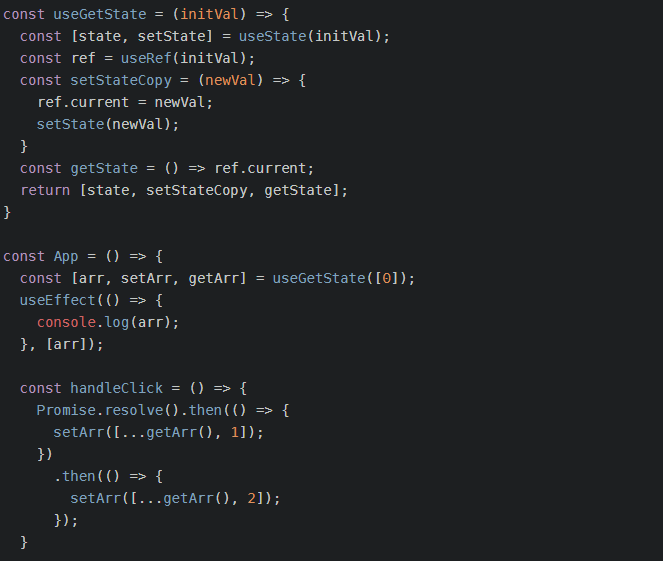
useGetState自定义hooks解决useState 异步回调获取不到最新值
setState 的两种传参方式 1、直接传入新值 setState(options); const [state, setState] useState(0); setState(state 1); 2、传入回调函数 setState(callBack); const [state, setState] useState(0); setState((prevState) > prevState 1); // prevState 是改变之…...
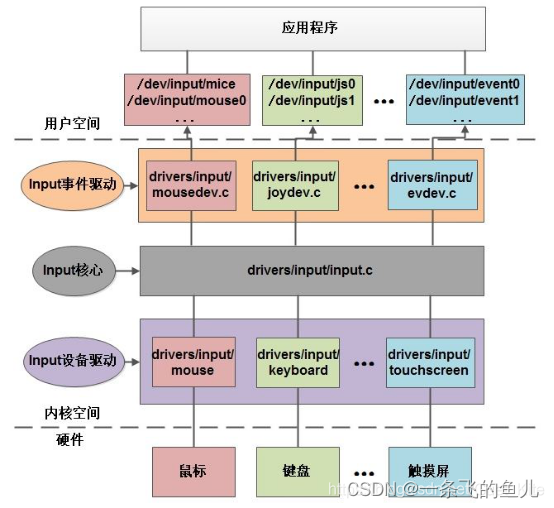
input子系统框架、外设驱动开发
一、input子系统基本框架 Linux内核为了两个目的： 简化纯输入类外设（如：键盘、鼠标、游戏杆、轨迹球、触摸屏。。。等等）的驱动开发统一输入类外设产生的数据格式（struct input_event），更加方…...
Google Chrome 浏览器以全屏模式打开
目录 前言以全屏模式打开禁止弹出无法更新的提示窗禁止翻译网页Chrome设置禁止翻译网页可能1可能2可能3 网页添加指令禁止Chrome翻译网页 禁用脚本气泡浏览器解决办法html解决办法方法1：鼠标滑过超链接时，使状态栏不出现超链接方法2：方法3&am…...
安装torch113、cuda116并运行demo【Transformer】
文章目录 01. 导读02. 显卡驱动版本03. 创建环境、下载安装必要包04. 运行参考代码： 01. 导读 安装torch113、cuda116并运行demo【Transformer】 02. 显卡驱动版本 C:\Users\Administrator>nvidia-smi -l 10 Wed Sep 13 23:35:08 2023 ----------------------…...
基于scRNA-seq的GRN分析三阴性乳腺癌的肿瘤异质性
三阴性乳腺癌即TNBC是一种肿瘤异质性高的乳腺癌亚型。最近的研究表明，TNBC患者可能包含具有不同分子亚型的细胞。此外，基于scRNA-seq数据构建的GRN已经证明了对关键调控因子研究的重要性。作者使用scRNA-seq对TNBC患者的GRN进行了全面分析。从scRNA-seq数…...
Python：二进制文件实现等间隔取相同数据量并合并
举例：每3byte为一页，每3页为一wl。将所有wl的第一页/第二页/第三页分别合并为一个文件。 data b\x01\x02\x03\x04\x05\x06\x07\x08\x09\x01\x02\x03\x04\x05\x06\x07\x08\x09\x01\x02\x03\x04\x05\x06\x07\x08\x09\x01\x02\x03\x04\x05\x06\x07\x08\x0…...
python使用openvc库进行图像数据增强
以下是使用Python和OpenCV库实现图像数据增强的简单示例代码，其中包括常用的数据增强操作： import cv2 import numpy as np import os# 水平翻转 def horizontal_flip(image):return cv2.flip(image, 1)# 垂直翻转 def vertical_flip(image):return cv2…...
如何利用Api接口获取手机当前的网络位置信息
在移动互联网时代，手机定位已经成为了一个日常化的需求，无论是导航、社交还是打车等服务都需要获取手机的位置信息。而获取手机位置信息最基础的一步就是获取手机当前的网络位置信息，本文将介绍如何利用API接口获取手机当前的网络位置信息。 …...
vue-elementPlus自动按需导入和主题定制
elementPlus自动按需导入 装包 -> 配置 1. 装包（主包和两个插件包） $ npm install element-plus --save npm install -D unplugin-vue-components unplugin-auto-import 2. 配置 在vite.config.js文件中配置，配置完重启（n…...
idea中dataBase模板生成
controller.java.vm ##定义初始变量 #set($tableName $tool.append($tableInfo.name, "Controller")) ##设置回调 $!callback.setFileName($tool.append($tableName, ".java")) $!callback.setSavePath($tool.append($tableInfo.savePath, "/contro…...
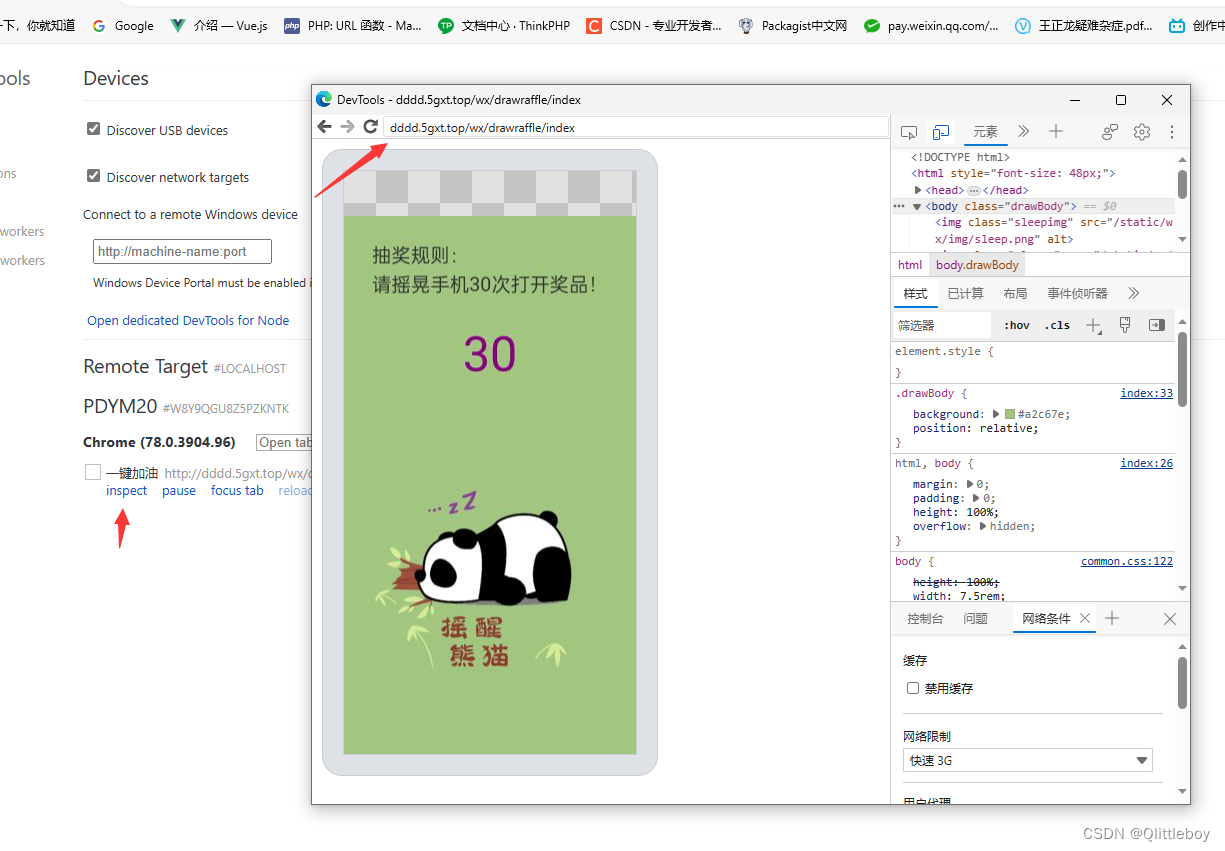
pc端测试手机浏览器运行情况，主要是测试硬件功能
测试h5震动摇晃等功能时不方便测试，需要连电脑显示调试数据 方法： 1.需要手机下载谷歌浏览器，pc端用edge或这谷歌浏览器 2.手机打开USB调试，打开要测试的网页 3.pc端地址栏输入edge://inspect/#devices（这里用的edge浏…...
软件概要设计-架构真题（二十五）
软件概要设计包括软件设计的结构、确定系统功能模块及其相互关系，主要采用（）描述程序的结构。（2018年） 程序流程图、PAD图和伪代码模块结构图、数据流图和盒图模块结构图、层次图和HIPO图程序流程图、数据流图和层次图…...
CSDN发文表情包整理
文章目录 简介部分Emoji表情符号简表人物自然物品地点符号 各种Emoji表情链接 简介 CSDN支持Markdown语法及Emoji表情，使用各种Emoji表情可以使得自己的博文更加生动多彩。一般有两种在支持Markdown的语法环境中添加Emoji表情：1.直接将表情包复制到文档…...
springBoot对接Apache POI 实现excel下载和上传
搭建springboot项目 此处可以参考 搭建最简单的SpringBoot项目_Steven-Russell的博客-CSDN博客 配置Apache POI 依赖 <dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId><version>5.2.2</version> </…...
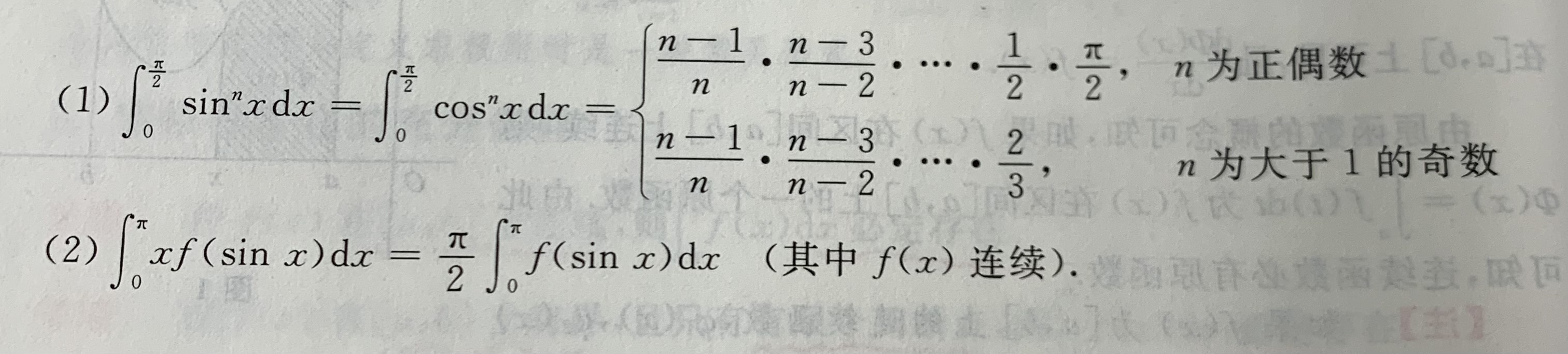
定积分的计算：牛顿-莱布尼茨公式
目录 牛顿-莱布尼茨公式 用C语言代码实现 利用换元积分法和分部积分法 利用奇偶性和周期性求积分 利用已有公式求积分 牛顿-莱布尼茨公式 牛顿-莱布尼茨公式（Newton-Leibniz formula）是微积分学中的基本定理之一，它反映了定积分与被积函…...
shell脚本之case 的用法
shell脚本之case case是Shell脚本中的一种控制流语句，它允许根据变量的值选择不同的执行路径。case语句的语法如下： case word in pattern [| pattern]...) command-list ;; pattern [| pattern]...) command-list ;; ... *) command-list ;; esa…...
第3章 helloworld 驱动实验（iTOP-RK3568开发板驱动开发指南 ）
在学习C语言或者其他语言的时候，我们通常是打印一句“helloworld”来开启编程世界的大门。学习驱动程序编程亦可以如此，使用helloworld作为我们的第一个驱动程序。 接下来开始编写第一个驱动程序—helloworld。 3.1 驱动编写 本小节来编写一个最简单的…...
变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计：let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性，这种设计体现了语言的核心哲学。以下是深度解析： 1.1 设计理念剖析 安全优先原则：默认不可变强制开发者明确声明意图 let x 5; …...
ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上，你可以使用apt包管理器来安装NFS服务器。打开终端并运行： sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享，例如/shared： sudo mkdir /shared sud…...
汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下，虚拟教学实训宛如一颗璀璨的新星，正发挥着不可或缺且日益凸显的关键作用，源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例，汽车生产线上各类…...
微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流，定义在 <sstream> 中： std::istringstream：输入流，从已有字符串中读取并解析。std::ostringstream：输出流，向内部缓冲区写入内容，最终取…...
自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效，它能挖掘数据中的时序信息以及语义信息，但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN，但是…...
多模态大语言模型arxiv论文略读（108）
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题：CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者：Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
MySQL 知识小结（一）
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库，分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷，但是文件存放起来数据比较冗余，用二进制能够更好管理咱们M…...
6个月Python学习计划 Day 16 - 面向对象编程（OOP）基础
第三周 Day 3 🎯 今日目标 理解类（class）和对象（object）的关系学会定义类的属性、方法和构造函数（init）掌握对象的创建与使用初识封装、继承和多态的基本概念（预告） &a…...
rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ，不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源（最常用） conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...