C语言练习题解析(2)
- 💓博客主页:江池俊的博客
- ⏩收录专栏:C语言刷题专栏
- 👉专栏推荐:✅C语言初阶之路 ✅C语言进阶之路
- 💻代码仓库:江池俊的代码仓库
- 🎉欢迎大家点赞👍评论📝收藏⭐

文章目录
- 🌴选择题
- 🌴编程题
- 📌尼科彻斯定理
- 📌等差数列
🎈前言:
- 本专栏每篇练习将包括
5个选择题 + 2个编程题,将涵盖C语言的不同方面,包括基础语法、数据类型、控制结构、数组、指针和函数等。通过练习,你将逐步掌握C语言的基础知识和常见问题,提高你的编程技巧和解决问题的能力。- 我希望这个博客能够为你提供有价值的练习资源,让你在实践中不断进步。同时,我们也鼓励你在练习过程中进行思考和创新,尝试使用不同的编程方法和技巧。
- 让我们一起挑战C语言练习题,攻克每一个难点,不断提升自己的编程技能!
在评论区分享你的练习心得和问题,与我们一起交流和成长。
🌴选择题
- 以下程序段的输出结果是( )
#include<stdio.h>
int main()
{char s[] = "\\123456\123456\t";printf("%d\n", strlen(s));return 0;
}
A: 12 B: 13 C: 16 D: 以上都不对

🔎正确答案:
A
【解析】:
这里考查转义字符,注意:\ \ 表示字符 ’ \ ',\123 表示字符 ‘{’,\t 表示制表符,这些都是一个字符。
- 若有以下程序,则运行后的输出结果是( )
#include <stdio.h>
#define N 2
#define M N + 1
#define NUM (M + 1) * M / 2
int main()
{printf("%d\n", NUM);return 0;
}
A: 4 B: 8 C: 9 D: 6

🔎正确答案:
B
【解析】:
宏只是替换,替换后NUM的样子是(2+1+1)*2+1/2,计算得8。
- 如下函数的 f(1) 的值为( )
int f(int n)
{static int i = 1;if (n >= 5)return n;n = n + i;i++;return f(n);
}
A: 5 B: 6 C: 7 D: 8

🔎正确答案:
C
【解析】:
此题注意静态局部变量的使用,static改变了i的生命周期,第一次调用函数:i初值是1,递归第二次调用函数时,i还是第一次那个变量,值已经变成了2,再一次调用函数时i就是3,依次类推.
- 下面3段程序代码的效果一样吗( )
int b;
(1)const int* a = &b;
(2)int const* a = &b;
(3)int* const a = &b;
A: (2)=(3) B: (1)=(2) C: 都不一样 D: 都一样
🔎正确答案:
B
【解析】:
const在*的左边,则指针指向的变量的值不可直接通过指针改变(可以通过其他途径改变);在*的右边,则指针的指向不可变。简记为 “左定值,右定向” ,(1)和(2)const都在*的左边,(3)中const在*的右边,所以应该选择B。
- 对于下面的说法,
正确的是( )
A: 对于 struct X{short s;int i;char c;},sizeof ( X )等于sizeof ( s ) + sizeof ( i ) + sizeof ( c )
B: 对于某个double变量 a,可以使用 a == 0.0 来判断其是否为零
C: 初始化方式 char a[14] = “Hello, world!”; 和char a[14]; a = “Hello, world!”;的效果相同
D: 以上说法都不对
🔎正确答案:
D
【解析】:
- A选项,没有考虑内存对齐。
- B选项,考察
double类型的比较,由于浮点数存在误差,不能直接判断两个数是否相等,通常 采用比较两数之差的绝对值是否小于一个很小的数字(具体的可自己设定这样一个数,作为误差)来确定是否相等。- C选项,
a为数组首地址是常量不能改变,- 所以A,B,C都是错的,选择D
🌴编程题
📌尼科彻斯定理
【牛客网链接:HJ76 尼科彻斯定理】
【题目信息】:

【答案解析】:
- 这道题的关键在于知道规律后,能够找到第
n个数据立方的起始奇数,从这个起始奇数开始,组成连续的n个奇数
项之和的表达式即可。 - 比如: 33 的起始奇数是 7 , 则 {7, 9, 11} 3个奇数求和表达式 7 + 9 + 11 。
而起始奇数有个规则: m3 的起始奇数值等于 m * (m - 1) + 1
奇数起始项规律:
首先所有奇数项构成一个差值为2的等差数列, 1 3 5 7 9 ....
其次,1的起始奇数是第1个等差数列项,2的起始奇数是第2个等差数列项,3的起始奇数是第4个等差数列项...
形成规律:
1 2 4 7....,而他们的差值分别是1 2 3 4 5...,所以第n项的起始奇数就是一个从1开始到n-1的等差数列(1 2 3 4 5....)之和+1
因此,
当需要求m的立方的起始奇数时,首先计算他的第一个奇数项是总体的第几个,然后再根据等差数列(1 3 5 7 9...)求这个起始奇数。
等差数列求和公式 Sn=n(a1+an)/2 ---> m * (m - 1) / 2 (计算奇数项是总体的第几个)
等差数列第n项公式 an=a1+(n-1)d ---> 1 + ((m * (m - 1) / 2) + 1 - 1) * 2 (计算这个起始奇数的值)
最终得到m的立方的表达式起始奇数: m * (m - 1) + 1 (最终的表达式)
//代码 1:
#include <stdio.h>
int main() {int m = 0;while (scanf("%d", &m) != EOF) {int start = m * m - m + 1;//找到起始奇数printf("%d", start);//先打印出起始奇数for (int i = 1; i < m; i++) //依次打印后面连续的m-1个奇数{printf("+%d", start + 2 * i);}printf("\n");}return 0;
}//代码 2:
#include <stdio.h>
int main()
{int m;while (~scanf("%d", &m)) {int start = m * (m - 1) + 1;//找到对应m^3的起始奇数char buf[10240] = { 0 };//sprintf(buf, format, ...) 与printf用法类似,格式化字符串但是不用于打印而是放到一个buf数组中sprintf(buf, "%d", start);//先将起始奇数转换成为字符串存入buf中for (int i = 1; i < m; i++) {//然后将紧随其后的m-1个奇数数字转换为字符串,按照指定格式放入buf中//%s+%d, 要求先有一个字符串,然后是+符号,然后是个数字的格式;buf对应原先的数据,start += 2对应紧随其后的奇数sprintf(buf, "%s+%d", buf, start += 2);}printf("%s\n", buf);} return 0;
}
【拓展】:sprintf 函数

下面是一些使用sprintf的例子:
- 基本的格式化
#include <stdio.h>int main() {char buffer[50];int a = 10;float b = 3.14;sprintf(buffer, "整数是 %d, 浮点数是 %f", a, b);printf("%s\n", buffer); // 输出: 整数是 10, 浮点数是 3.140000return 0;
}
- 使用标志符
#include <stdio.h>int main() {char buffer[50];int a = 10;float b = 3.14;sprintf(buffer, "整数是 %2d, 浮点数是 %6.2f", a, b);printf("%s\n", buffer); // 输出: 整数是 10, 浮点数是 3.1400return 0;
}
在这个例子中,%2d表示将整数输出为至少两位的数,如果不足两位则在前面补一个空格。%6.2f表示将浮点数输出为至少6位的数,其中小数点后有两位,如果不足则补0。
这只是sprintf函数的基本用法,实际上它还有许多更复杂的用法和标志符,可以用来处理各种复杂的字符串格式化需求。
📌等差数列
【牛客网链接:HJ100 等差数列】
【题目信息】:

【答案解析】:
- 这道题了解了等差数列求和公式
Sn=n(a1+an)/2就简单了 ,根据题目得知a1=2,而等差数列第n项也有具体公式
an=a1+(n-1)d,而公差为3, 这时候只需要套入公式计算即可。
#include <stdio.h>
int main()
{int n, a1 = 2;while (~scanf("%d", &n)) {int an = a1 + (n - 1) * 3;//等差数列第n项计算printf("%d\n", n * (a1 + an) / 2); //等差数列求和打印} return 0;
}
- 这题也可以遍历一遍等差数列,依次求和。
#include<stdio.h>
int main() {int n;while (EOF != scanf("%d", &n)) {int sum = 0;for (int i = 2; i <3* n+2; i+=3) //等差数列第n项的值为3*(n-1)+2{sum += i;//计算前n项和}printf("%d\n", sum);}return 0;
}
🔥今天的内容就到这里了,有什么问题的话欢迎大家在评论区讨论,也可以私信博主为你解答,如果觉得博主的文章还不错的话, 请👍三连支持一下博主哦🤞

相关文章:

C语言练习题解析(2)
💓博客主页:江池俊的博客⏩收录专栏:C语言刷题专栏👉专栏推荐:✅C语言初阶之路 ✅C语言进阶之路💻代码仓库:江池俊的代码仓库🎉欢迎大家点赞👍评论📝收藏⭐ 文…...
Element UI 表单验证规则动态失效问题
Element 版本:v2.15.3 问题背景 如下代码所示:有一个上传文件的 input 组件,在更新的时候,如果不上传文件表示不更新,如果要更新则点击 「重新上传」按钮将上传组件显示出来 <el-form ref"form" :mode…...
多线程并发篇
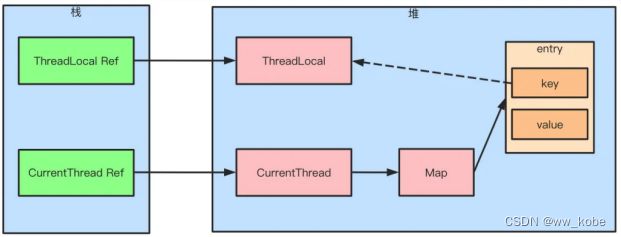
目录 1、线程生命周期 2、线程创建方式 3、Callable 与 Future 4、如何停止一个正在运行的线程 5、notify() 和 notifyAll() 的区别 6、sleep() 和 wait() 的区别 7、start() 和 run() 的区别 8、interrupted 和 isInterruptedd 的区别 9、CyclicBarrier 和 Count…...

pycharm-2023.1 closing project window stuck
pycharm-2023.1 closing project window stuck 问题描述 pycharm 切换项目/重启,一直卡在 closing project 原因分析 PyCharm 2023.1 issue - closing project window stuck (PyPIPackageUtil.lambda$parsePyPIListFromWeb) 解决方案 升级 pycharm 到 2023.3py…...

tkinter编写的打开csdn程序
目录 鬼畜tkinter简介程序代码解析现成总结鬼畜 看看你每次打开CSDN: 1.开机 2.打开浏览器 3.打开CSDN 4.等待 5.完成 我: 1.开机 2.点击%%%按钮 3.等待 4.完成 简单了不知道多少倍 上面的纯属鬼畜,下面正文!!! tkinter tkinter是一个用于创建图形用户界面(GUI)的Py…...

Vue3.2组件如何封装,以弹窗组件的封装为例
以前一直想,每次封装一个弹窗组件的时候,一直特别复杂,父传子,子传父,各种来回绕,来回修改。 一直想如何才能更加简化,但是一直没时间,今天终于抽时间出来封装了一下 本次封装简化…...
每天10个小知识点)
Vue知识系列(5)每天10个小知识点
目录 系列文章目录Vue知识系列(1)每天10个小知识点Vue知识系列(2)每天10个小知识点Vue知识系列(3)每天10个小知识点Vue知识系列(4)每天10个小知识点 知识点41.vue常用基本指令有哪些…...
)
Java基础题08——数组(查找下标所对应的值)
给定一个整数数组,输入一个值 n ,输出 n *在数组中的下标 **(*如果不存在输出 -1 ) 如:int[] arr {3, 2, 1, 4, 5}; 1 输入: 3 输出: 0 2. 输入: 6 输出: -1 int[] arr new int[]{3, 2, 1, 4,…...

LinkedList 源码分析
LinkedList 是一个基于双向链表实现的集合类。 LinkedList 插入和删除元素的时间复杂度 头部插入/删除:只需要修改头结点的指针即可完成插入/删除操作,因此时间复杂度为 O(1)。尾部插入/删除:只需要修改尾结点的指针即可完成插入/删除操作…...
)
跑步锻炼(蓝桥杯)
跑步锻练 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小蓝每天都锻炼身体。 正常情况下,小蓝每天跑 1 千米。如果某天是周一或者月初(1 日),为了激励自己&#x…...

【SLAM】视觉SLAM简介
【SLAM】视觉SLAM简介 task04 主要了解了SLAM的主流框架,清楚VSALM中间接法与直接法的主要区别在什么地方,其各自的优势是什么,了解前端与后端的关系是什么 1.什么是SLAM 2.VSALM中间接法与直接法的主要区别在什么地方,其各自的…...
Visual Studio2019报错
1- Visual Studio2019报错 错误 MSB8036 找不到 Windows SDK 版本 10.0.19041.0的解决方法 小伙伴们在更新到Visual Studio2019后编译项目时可能遇到过这个错误:“ 错误 MSB8036 找不到 Windows SDK 版本 10.0.19041.0的解决方法”,但是我们明明安装了该…...

ffplay源码解析-PacketQueue队列
包队列架构位置 对应结构体源码 MyAVPacketList typedef struct MyAVPacketList {AVPacket pkt; //解封装后的数据struct MyAVPacketList *next; //下一个节点int serial; //播放序列 } MyAVPacketList;PacketQueue typedef struct PacketQueue {MyAVPacketList …...

Flowable主要API介绍
1. ProcessEngine 负责与各个服务进行交互和管理流程的整个生命周期。 方法描述getName()close()startExecutors()启动所有流程引擎中的执行器。执行器用于处理流程实例的执行,在引擎启动时,执行器会自动运行并处理待办任务和定时任务。getRepositorySe…...

TensorFlow与pytorch特定版本虚拟环境的安装
TensorFlow与Python的版本对应,注意,一定要选择对应的版本,否则会让你非常痛苦,折腾很久搞不清楚原因。 建议使用国内镜像源安装 没有GPU后缀的就表示是CPU版本的,不加版本就是最新 pip install tensorflow -i https:…...

【SpringMVC】拦截器JSR303的使用
【SpringMVC】拦截器&JSR303的使用 1.1 什么是JSR3031.2 为什么使用JSR3031.3 常用注解1.4 Validated与Valid区别1.5 JSR快速入门1.5.2 配置校验规则# 1.5.3 入门案例二、拦截器2.1 什么是拦截器2.2 拦截器与过滤器2.3 应用场景2.4 拦截器快速入门2.5.拦截器链2.6登录案列权…...

Java - LambdaQueryWrapper 的常用方法
1、查看项目中是否导入mybatisPlus的jar包 2、servie 层和实现类要集成mybatisPlus service 继承IService<> 实现类中要继承IService的实现类ServiceImpl<mapper,实体类> 3、如果想要mapper中的一些方法,mapper 要继承BaseMapper<实体类> 4、在实…...

Selenium常见问题解析
1、元素定位失败: 在使用Selenium自动化测试时,最常见的问题之一是无法正确地定位元素,这可能导致后续操作失败。解决方法包括使用不同的定位方式(如xpath、CSS selector、id等),等待页面加载完全后再进行…...
【npm】npm私有库的使用-绑定
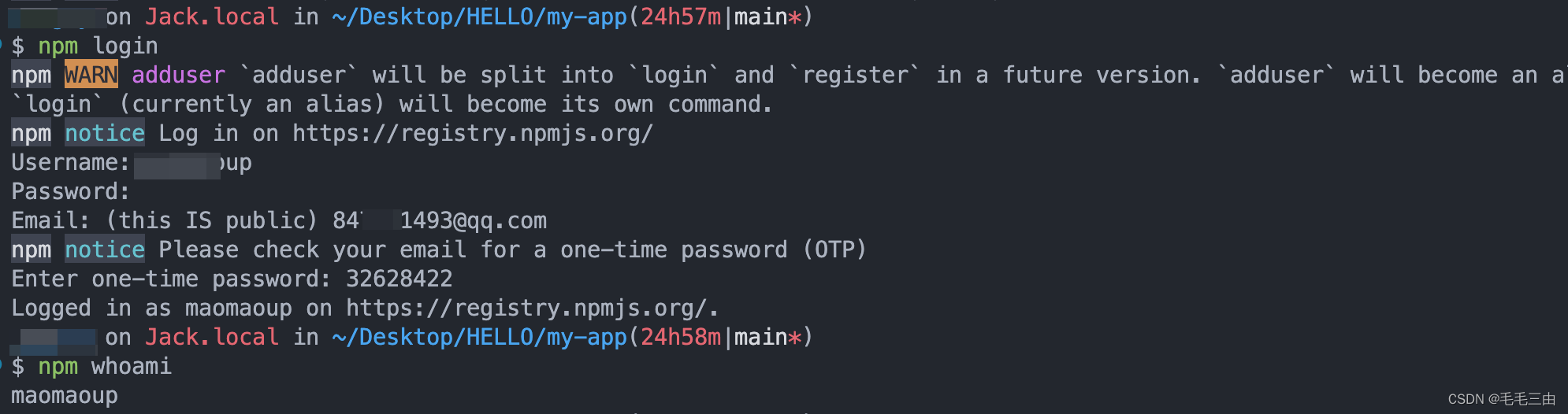
注册npm账户 输入基本信息 验证 收一次性验证码 登录 本地绑定 全局绑定了其他的私有库 若要在专门发包的项目中,发包到自己的私有库,需要在项目文件夹中创建一个.npmrc文件 创建文件 可以直接在项目目录下输入touch .npmrc创建文件 文件内容 regi…...

spring seccurity OAuth 2.0授权服务器工作流程
一、客户端配置:在configure(ClientDetailsServiceConfigurer clients)方法中,配置了一个客户端,包括客户端标识符、客户端秘密、授权类型、授权范围和令牌有效期等信息。这个客户端表示某个应用程序或服务,它将向授权服务器请求访…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
