数据结构与算法之最短路路径与最短路径和动态规划
If every unfolding we experience takes us further along in life, then, we are truly experiencing what life is offering.
如果我们在人生中体验的每一次转变都让我们在生活中走得更远,那么,我们就真正的体验到了生活想让我们体验的东西。
Do not try and bend the spoon. That's impossible. Instead, only try to realize the truth. There is no spoon. Then you'll see that it is not the spoon that bends. It is only yourself.
不要试图弯曲汤匙。那是不可能的。你只能试着去理解一件事实。汤匙不存在。你会发现被弯曲的不是汤匙。那只是你自己。
目录:
一.题目(最短路径)
1.关于动态规划
二.三种思路
1.思路一(深搜)
2.思路二(动态规划)
3.思路三(数论方法)
总结
三.题目(最短路径和)
一.题目(最短路径)
1.关于动态规划
动态规划算法的基本思想是:将待求解的问题分解成若干个相互联系的子问题,先求解子问题,然后从这些子问题的解得到原问题的解;对于重复出现的子问题,只在第一次遇到的时候对它进行求解,并把答案保存起来,让以后再次遇到时直接引用答案,不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果。
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为Finish)。
问总共有多少条不同的路径?

输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 2, n = 3
输出:3
解释: 从左上角开始,总共有 3 条路径可以到达右下角。
向右 -> 向右 -> 向下
向右 -> 向下 -> 向右
向下 -> 向右 -> 向右
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9
二.三种思路
思路一(深搜)
这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。
注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
如图举例:

此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
class Solution {
private:int dfs(int i, int j, int m, int n) {if (i > m || j > n) return 0; // 越界了if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);}
public:int uniquePaths(int m, int n) {return dfs(1, 1, m, n);}
};大家如果提交了代码就会发现超时了!
来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。
这棵树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
2.思路二(动态规划)
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
1)确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2)确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
3)dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
所以初始化代码为:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;4)确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
5)举例推导dp数组
如图所示:

以上动规五部曲分析完毕,C++代码如下:
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m; i++) dp[i][0] = 1;for (int j = 0; j < n; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};时间复杂度:O(m × n)
空间复杂度:O(m × n)
3.思路三(数论方法)
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。

在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
那么这就是一个组合问题了。
那么答案,如图所示:

求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
例如如下代码是不行的。
class Solution {
public:int uniquePaths(int m, int n) {int numerator = 1, denominator = 1;int count = m - 1;int t = m + n - 2;while (count--) numerator *= (t--); // 计算分子,此时分子就会溢出for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母return numerator / denominator;}
};需要在计算分子的时候,不断除以分母,代码如下:
class Solution {
public:int uniquePaths(int m, int n) {long long numerator = 1; // 分子int denominator = m - 1; // 分母int count = m - 1;int t = m + n - 2;while (count--) {numerator *= (t--);while (denominator != 0 && numerator % denominator == 0) {numerator /= denominator;denominator--;}}return numerator;}
};时间复杂度:O(m)
空间复杂度:O(1)
计算组合问题的代码还是有难度的,特别是处理溢出的情况!
总结
本文分别给出了深搜,动规,数论三种方法。
深搜当然是超时了,顺便分析了一下使用深搜的时间复杂度,就可以看出为什么超时了。然后在给出动规的方法,依然是使用动规五部曲,这次我们就要考虑如何正确的初始化了,初始化和遍历顺序其实也很重要!
三.题目(最短路径和)
给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。
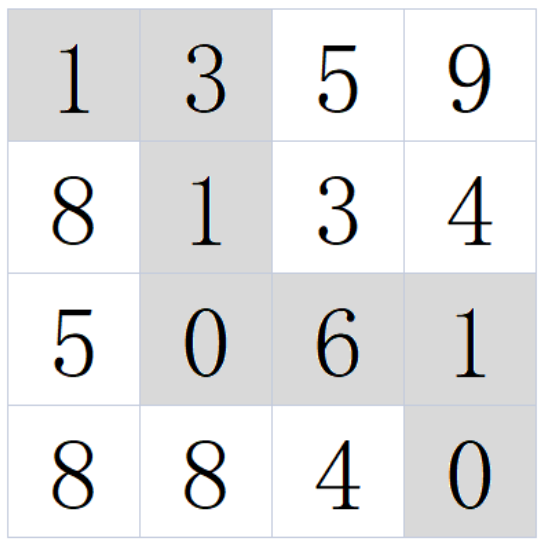
例如:当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时,对应的返回值为12,
所选择的最小累加和路径如下图所示:

1.思路
最朴素的解法莫过于枚举所有的路径,然后求和,找出其中最大值。但是像这种有状态值可以转移的问题,我们可以尝试用动态规划。
具体做法:
step 1:我们可以构造一个与矩阵同样大小的二维辅助数组,其中]dp[i][j]表示以(i,j)位置为终点的最短路径和,则dp[0][0]=matrix[0][0]。
step 2:很容易知道第一行与第一列,只能分别向右或向下,没有第二种选择,因此第一行只能由其左边的累加,第一列只能由其上面的累加。
step 3:边缘状态构造好以后,遍历矩阵,补全矩阵中每个位置的dp数组值:如果当前的位置是(i,j),上一步要么是(i−1,j)往下,要么就是(i,j−1)往右,那么取其中较小值与当前位置的值相加就是到当前位置的最小路径和,因此状态转移公式为dp[i][j]=min(dp[i−1][j],dp[i][j−1])+matrix[i][j]。
step 4:最后移动到(n−1,m−1)的位置就是到右下角的最短路径和。
2.代码实现
class Solution {
public:int minPathSum(vector<vector<int> >& matrix) {// write code hereint m=matrix.size();int n=matrix[0].size();vector<vector<int>>dp(m,vector<int>(n,0));dp[0][0]=matrix[0][0];for(int i=1;i<m;i++){dp[i][0]=dp[i-1][0]+matrix[i][0];}for(int j=1;j<n;j++){dp[0][j]=dp[0][j-1]+matrix[0][j];}for(int i=1;i<m;i++){for(int j=0;j<n;j++){dp[i][j]=min(dp[i-1][j],dp[i][j-1])+matrix[i][j];}}return dp[m-1][n-1];}
};这是两道经典的dp题目,值得反反复思琢磨。
2023.02.23
From:努力进大厂的新青年
相关文章:

数据结构与算法之最短路路径与最短路径和动态规划
If every unfolding we experience takes us further along in life, then, we are truly experiencing what life is offering.如果我们在人生中体验的每一次转变都让我们在生活中走得更远,那么,我们就真正的体验到了生活想让我们体验的东西。Do not tr…...
git 本地新建分支并进行合并
由于新的要求 不允许在线上直接clone下的git分支进行开发,只能本地新建分支再往线上分支合并远程库clone到本地库 git clone 需要下载的git地址注意我下载下来的是dev分支 根据实际情况进行分析git clone https://gitee.com/hello.git本地创建新的分支 git checkout…...

2023年DAMA-CDGA/CDGP数据治理认证选择哪家机构好?
DAMA认证为数据管理专业人士提供职业目标晋升规划,彰显了职业发展里程碑及发展阶梯定义,帮助数据管理从业人士获得企业数字化转型战略下的必备职业能力,促进开展工作实践应用及实际问题解决,形成企业所需的新数字经济下的核心职业…...
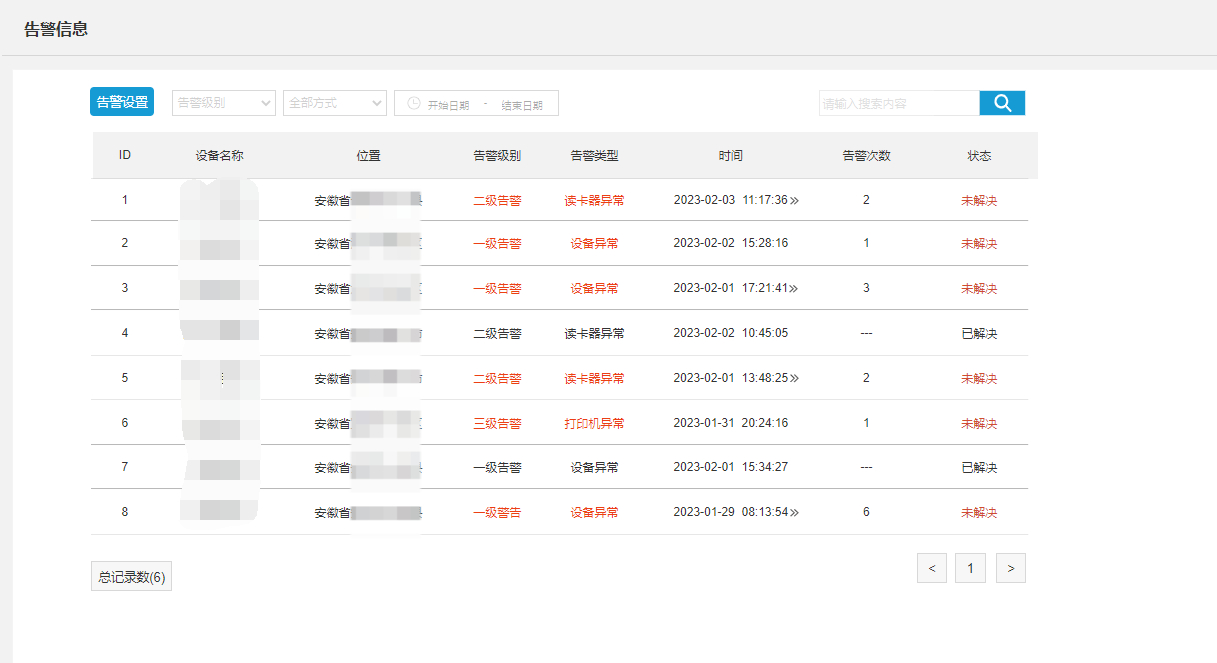
浅析高速服务区交互一体机设备管理系统的建设与方向
很多高速公路服务区均缺乏现代化的服务思维、理念和手段,信息系统功能薄弱,服务区的自助服务终端存在功能单一、人机交互体验差、设备维护管理成本高、联动效率低、运营难等问题,这不仅无法支撑服务区的精细化服务和智能化管理需求࿰…...
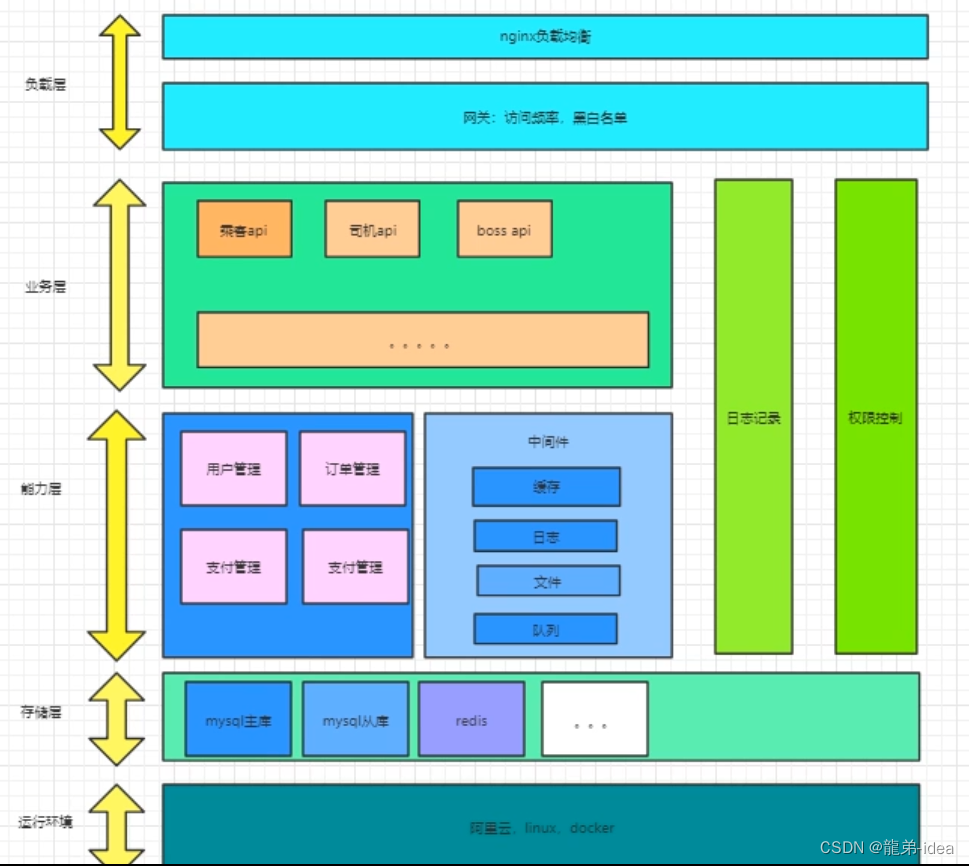
分布式面试题
目录 分布式id的生成方案有哪些 雪花算法生成的ID由哪些部分组成 分布式锁在项目中有哪些应用场景? 分布式锁有哪些解决方案 Redis做分布式锁用什么命令 Redis做分布式锁,死锁有哪些情况?如何解决 Redis如何做分布式锁 MySQL如何做分布式锁 什么…...

Prophet 处理时间序列数据
Prophet 处理时间序列数据 flyfish 论文地址 https://peerj.com/preprints/3190/ 官网 https://facebook.github.io/prophet/ 源码地址 https://github.com/facebook/prophet hon import pandas as pd from prophet import Prophet df pd.read_csv(https://raw.githubuse…...

一文搞清楚LoRa网关,LoRa网关全知道
欢迎来到东用知识小课堂下面,今天我们用东用科技的OGC300系列LoRa为例,以简单的方式帮助大家了解一下LoRa相关的小知识一、LoRa网关的基本介绍LoRa是semtech公司创建的低功耗局域网无线标准,低功耗一般很难覆盖远距离,远距离一般功…...
医疗保健和智慧城市服务将引领5G物联网采用
Juniper Research预测,到2026年,全球5G物联网连接将达到1.16亿,而2023年仅为1700万。该公司预测,医疗保健部门和智慧城市服务将在未来三年推动这1100%的增长,到2026年占5G物联网设备的60%以上。5G物联网技术的超低延迟…...

promise静态方法及相关练习
promise的静态方法相对简单,这篇文章做个总结,以便漏补缺总结如下:1. Promise.all/Promise.anyPromise.allSettled/Promise.race都是接受数组,数组里面是promise2.. Promise.all 接收的promise数组只要有一个失败那么整个就是失败…...

【Tips】通过背数据了解业务
学习资料:做了三年数据分析,给你的几点建议 1. 通过背数据了解业务 原文: 总结: 方法:每天早上去到公司第一件事情就是先背一遍最新的各种指标。原理: 数据敏感性就是建立在对数据的了解和熟悉上。业务的…...
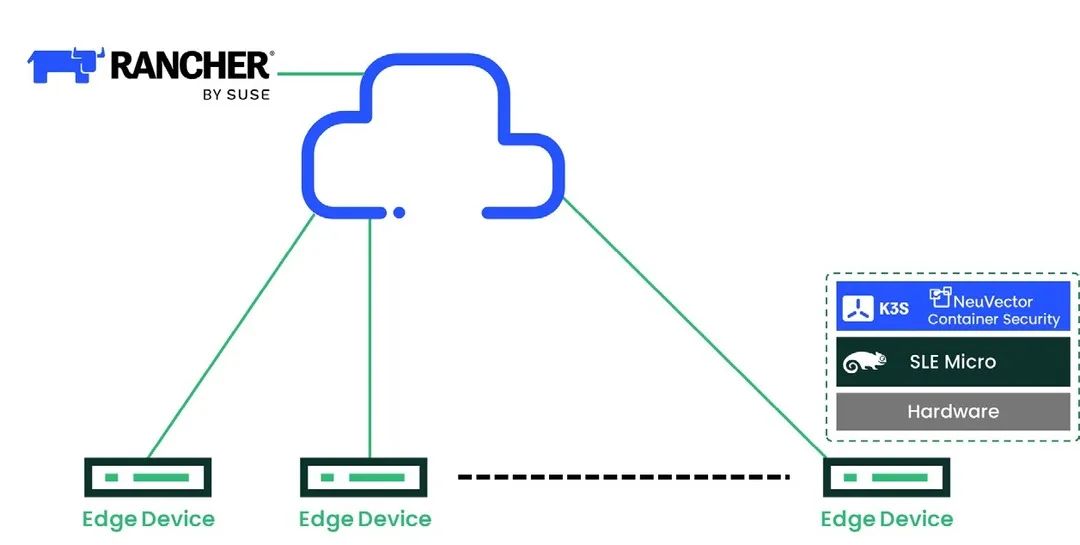
设备太分散?如何一站式管理边缘 OS、K8s 和应用?
作者简介 张志龙,SUSE 大中华区资深解决方案架构师,CNCF 官方认证的 CKA&CKAD 工程师,深耕以 Kubernetes 为代表的云原生领域,具备丰富的架构设计、业务容器化改造和项目落地实践经验。 据 Gartner 预测,到 2025 年…...

CF1692D The Clock 题解
CF1692D The Clock 题解题目链接字面描述题面翻译题目描述输入输出题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示代码实现题目 链接 https://www.luogu.com.cn/problem/CF1692D 字面描述 题面翻译 题目描述 从一个24小时制的时间点开始,每隔 xx…...
IDEA 30 个好用天花板技巧,敲代码直接接爽到飞。
IDEA 作为Java开发工具的后起之秀,几乎以碾压之势把其他对手甩在了身后,主要原因还是归功于:好用;虽然有点重,但依旧瑕不掩瑜,内置了非常多的功能,大大提高了日常的开发效率,下面汇总…...
关于selenium的等待
目录 隐式等待 显式等待 注意事项 隐式等待 简单来说:在规定的时间范围内,轮询等待元素出现之后就立即结束。 如果在规定的时间范围内,元素仍然没有出现,则会抛出一个异常【NoSuchElementException】,脚本停止运行…...
结构建模设计——Solidworks软件之装配体操作基本总结三(高级配合、机械配合、快捷菜单功能)
【系列专栏】:博主结合工作实践输出的,解决实际问题的专栏,朋友们看过来! 《QT开发实战》 《嵌入式通用开发实战》 《从0到1学习嵌入式Linux开发》 《Android开发实战》 《实用硬件方案设计》 长期持续带来更多案例与技术文章分享…...
【在 Colab 中使用 TensorBoard 绘图】
【在 Colab 中使用 TensorBoard 绘图】进入 Google Drive进入 Colab在深度学习中,使用本机GPU跑可能会比较慢,这里使用 Google Drive Colab 进行训练,运行代码 进入 Google Drive 进入网盘 初次进入需要注册账号。注意科学上网即可。右键…...

React循环DOM时为什么需要添加key
一、React 渲染流程和更新流程 react渲染流程:jsx -> 虚拟dom -> 真实domreact更新流程:props/state改变 -> render函数重新执行 -> 生成新的虚拟dom树 -> 新旧虚拟dom树进行diff -> 计算出差异进行更新 ->更新到真实的dom树 所以…...

Elasticsearch架构篇 - terms aggregation
terms aggregation 即词项分桶聚合。它是 Elasticsearch 最常用的聚合,类同于关系型数据库依据关键字段做 group。 size:返回的词项分桶数量,默认 10。阈值 65535。默认情况下,协调节点向每个分片请求 top size 数量的词项桶&…...

MySQL 的体系结构、引擎与索引
MySQL的引擎与体系结构 体系结构 连接层 最上层是一些客户端和链接服务,主要完成一些类似于连接处理、授权认证、及相关的安全方案。服务器也会为安全接入的每个客户端验证它所具有的操作权限 服务层 第二层架构主要完成大多数的核心服务功能,如SQL…...

数字IC设计需要学什么?
看到不少同学在网上提问数字IC设计如何入门,在学习过程中面临着各种各样的问题,比如书本知识艰涩难懂,有知识问题难解决,网络资源少,质量参差不齐。那么数字IC设计到底需要学什么呢? 首先来看看数字IC设计…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
