LeetCode 周赛上分之旅 #49 再探内向基环树
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。
学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度也更复杂。在这个专栏里,小彭与你分享每场 LeetCode 周赛的解题报告,一起体会上分之旅。
本文是 LeetCode 上分之旅系列的第 49 篇文章,往期回顾请移步到文章末尾~
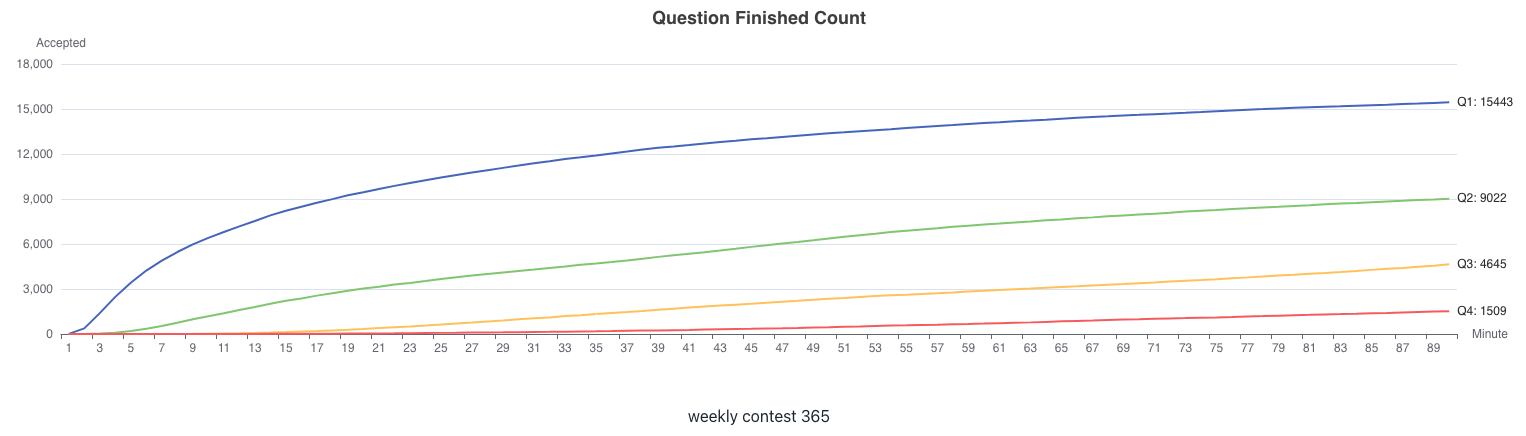
LeetCode 周赛 365
T1. 有序三元组中的最大值 I(Easy)
- 标签:模拟、前后缀分解、线性遍历
T2. 有序三元组中的最大值 II(Medium)
- 标签:模拟、前后缀分解、线性遍历
T3. 无限数组的最短子数组(Medium)
- 标签:滑动窗口
T4. 有向图访问计数(Hard)
- 标签:内向基环树、拓扑排序、DFS
T1. 有序三元组中的最大值 I(Easy)
https://leetcode.cn/problems/maximum-value-of-an-ordered-triplet-i/description/
同 T2。
T2. 有序三元组中的最大值 II(Medium)
https://leetcode.cn/problems/maximum-value-of-an-ordered-triplet-ii/description/
问题分析
初步分析:
- 问题目标: 构造满足条件的合法方案,使得计算结果最大;
- 问题条件: 数组下标满足 i < j < k i < j < k i<j<k 的三位数;
- 计算结果: ( n u m s [ i ] − n u m s [ j ] ) ∗ n u m s [ k ] (nums[i] - nums[j]) * nums[k] (nums[i]−nums[j])∗nums[k]。
思考实现:
- T1. 有序三元组中的最大值 I 的数据量只有 100 100 100,枚举所有合法的 [ i , j , k ] [i, j, k] [i,j,k] 组合,时间复杂度是 O ( n 3 ) O(n^3) O(n3);
- T2. 有序三元组中的最大值 II 的数据量有 1 0 5 10^5 105,我们需要思考更优解法。
思考优化:
为了使得计算结果尽可能大,显然应该让乘法的左右两部分尽可能大。对于存在多个变量的问题,一个重要的技巧是 「固定一个,思考另一个」 ,这就容易多了。
- 固定 j j j: 为了让结果更大,应该找到 n u m s [ j ] nums[j] nums[j] 左边最大的 n u m s [ i ] nums[i] nums[i] 和右边最大的 n u m s [ k ] nums[k] nums[k] 组合,时间复杂度是 O ( n 2 ) O(n^2) O(n2)。我们也可以使用前后缀分解预处理出来,这样时间复杂度就是 O ( n ) O(n) O(n);
- 固定 k k k: 同理,固定 k k k 寻找应该找到左边使得 n u m s [ i ] − n u m s [ j ] nums[i] - nums[j] nums[i]−nums[j] 最大的方案,这可以实现线性时间和常量空间。
题解一(枚举)
枚举所有方案,记录最优解。
class Solution {fun maximumTripletValue(nums: IntArray): Long {var ret = 0Lval n = nums.sizefor (i in 0 until n) {for (j in i + 1 until n) {for (k in j + 1 until n) {ret = max(ret, 1L * (nums[i] - nums[j]) * nums[k])}}}return ret}
}
复杂度分析:
- 时间复杂度: O ( n 3 ) O(n^3) O(n3)
- 空间复杂度: O ( 1 ) O(1) O(1)
题解二(前后缀分解)
预处理出每个位置前后的最大值,再枚举 n u m s [ j ] nums[j] nums[j] 记录最优解。
class Solution {fun maximumTripletValue(nums: IntArray): Long {val n = nums.sizeval preMax = IntArray(n)var sufMax = IntArray(n)for (i in 1 until n) {preMax[i] = max(preMax[i - 1], nums[i - 1])}for (i in n - 2 downTo 0) {sufMax[i] = max(sufMax[i + 1], nums[i + 1])}return max(0, (1 .. n - 2).maxOf { 1L * (preMax[it] - nums[it]) * sufMax[it] })}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
题解三(线性遍历)
线性遍历 n u m s [ k ] nums[k] nums[k] 并记录 ( n u m s [ i ] − n u m s [ j ] ) (nums[i] - nums[j]) (nums[i]−nums[j]) 的最大值,记录最优解。
class Solution {fun maximumTripletValue(nums: IntArray): Long {val n = nums.sizevar ret = 0Lvar maxDelta = 0var maxI = 0for (e in nums) {ret = max(ret, 1L * maxDelta * e)maxDelta = max(maxDelta, maxI - e)maxI = max(maxI, e)}return ret}
}
class Solution:def maximumTripletValue(self, nums: List[int]) -> int:ret = maxDelta = maxI = 0for e in nums:ret = max(ret, maxDelta * e)maxDelta = max(maxDelta, maxI - e)maxI = max(maxI, e)return ret
class Solution {
public:long long maximumTripletValue(vector<int> &nums) {long long ret = 0;int max_delta = 0, max_i = 0;for (int e : nums) {ret = max(ret, (long long) max_delta * e);max_delta = max(max_delta, max_i - e);max_i = max(max_i, e);}return ret;}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) O(1) O(1)
T3. 无限数组的最短子数组(Medium)
https://leetcode.cn/problems/minimum-size-subarray-in-infinite-array/description/
问题分析
令 n u m s nums nums 数组的整体元素和为 s s s,考虑 t a r g e t target target 的两种情况:
- 对于 t a r g e t target target 很小的情况(小于数组整体和 s s s):这是很简单的滑动窗口问题;
- 对于 t a r g e t target target 较大的情况(大于等于数组的整体和 s s s):那么最小长度中一定包含整数倍的 s s s,以及某个 n u m s nums nums 的子数组。
class Solution {fun minSizeSubarray(nums: IntArray, t: Int): Int {val n = nums.sizeval s = nums.sum()val k = t % s// 同向双指针var left = 0var sum = 0var len = nfor (right in 0 until 2 * n) {sum += nums[right % n]while (sum > k) {sum -= nums[left % n]left ++}if (sum == k) len = min(len, right - left + 1)}return if (len == n) -1 else n * (t / s) + len}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 最大扫描 2 2 2 倍数组长度;
- 空间复杂度:仅使用常量级别空间。
T4. 有向图访问计数(Hard)
https://leetcode.cn/problems/count-visited-nodes-in-a-directed-graph/description/
问题分析
初步分析:
对于 n n n 个点 n n n 条边的有向弱连通图,图中每个点的出度都是 1 1 1,因此它是一棵 「内向基环树」。那么,对于每个点有 2 2 2 种情况:
- 环上节点:绕环行走一圈后就会回到当前位置,因此最长访问路径就是环长;
- 树链节点:那么从树链走到环上后也可以绕环行走一圈,因此最长访问路径就是走到环的路径 + 环长。
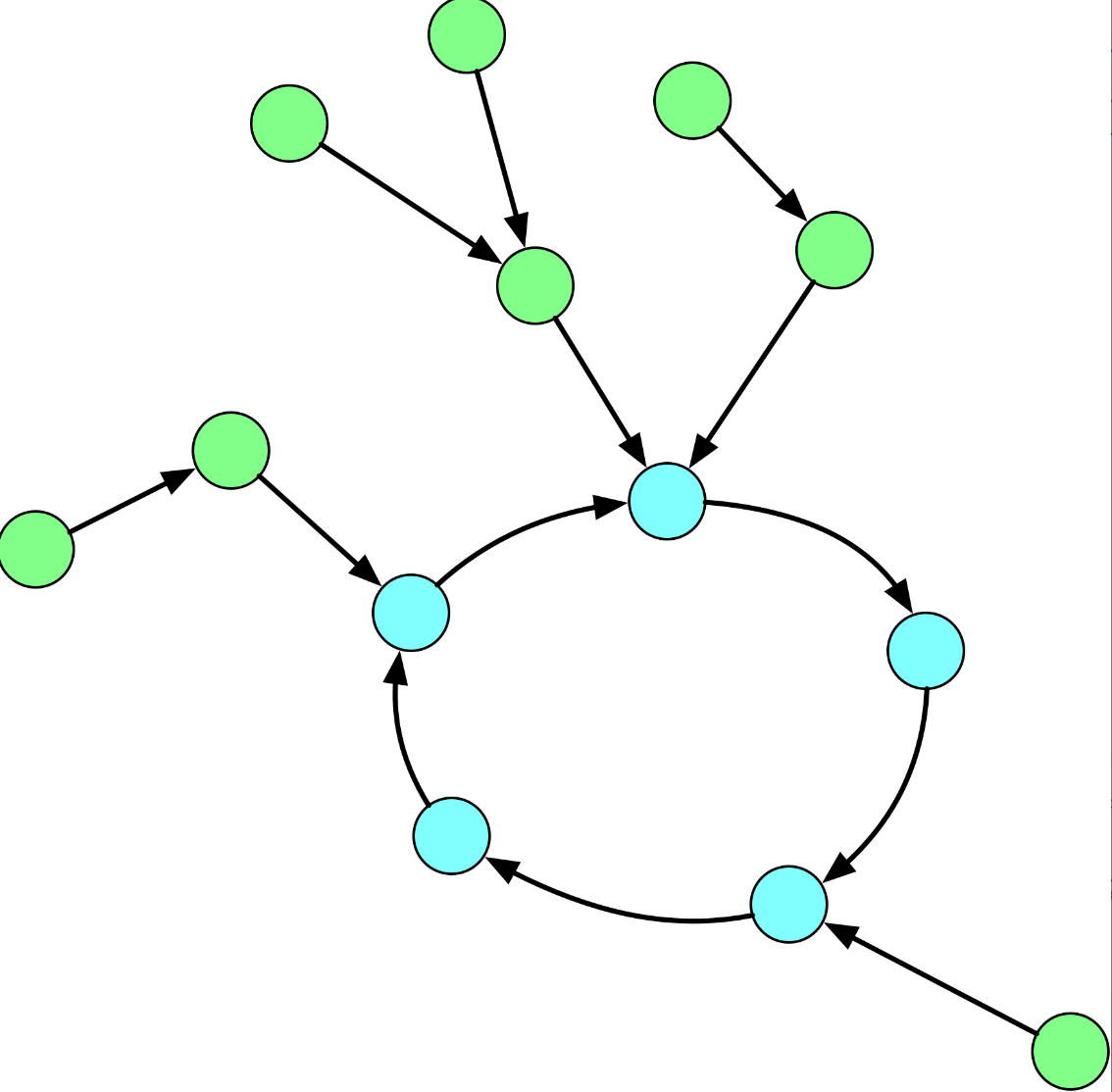
图片不记得出处了~
思考实现:
- 只有一个连通分量的情况: 那么问题就相对简单,我们用拓扑排序剪去树链,并记录链上节点的深度(到环上的距离),最后剩下的部分就是基环;
- 有多个连通分量的情况: 我们需要枚举每个连通分量的基环,再将基环的长度累加到该连通分量的每个节点。
题解(拓扑排序 + DFS)
- 第一个问题:将基环的长度累加到该连通分量的每个节点
拓扑排序减去树链很容易实现,考虑到我们这道题在找到基环后需要反向遍历树链,因此我们考虑构造反向图(外向基环树);
- 第二个问题:找到基环长度
在拓扑排序后,树链上节点的入度都是 0 0 0,因此入度大于 0 0 0 的节点就位于基环上。枚举未访问的基环节点走 DFS,就可以找到该连通分量的基环。
class Solution {fun countVisitedNodes(edges: List<Int>): IntArray {// 内向基环树val n = edges.sizeval degree = IntArray(n)val graph = Array(n) { LinkedList<Int>() }for ((x,y) in edges.withIndex()) {graph[y].add(x)degree[y]++ // 入度}// 拓扑排序val ret = IntArray(n)var queue = LinkedList<Int>()for (i in 0 until n) {if (0 == degree[i]) queue.offer(i)}while(!queue.isEmpty()) {val x = queue.poll()val y = edges[x] if (0 == -- degree[y]) queue.offer(y)}// 反向 DFSfun rdfs(i: Int, depth: Int) {for (to in graph[i]) {if (degree[to] == -1) continueret[to] = depthrdfs(to, depth + 1)}}// 枚举连通分量for (i in 0 until n) {if (degree[i] <= 0) continueval ring = LinkedList<Int>()var x = iwhile (true) {degree[x] = -1ring.add(x)x = edges[x]if (x == i) break}for (e in ring) {ret[e] = ring.sizerdfs(e, ring.size + 1)}}return ret}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 拓扑排序和 DFS 都是线性时间;
- 空间复杂度: O ( n ) O(n) O(n) 图空间和队列空间。
题解二(朴素 DFS)
思路参考小羊的题解。
我们发现这道题的核心在于 「找到每个基环的节点」 ,除了拓扑排序剪枝外,对于内向基环树来,从任何一个节点走 DFS 走到的最后一个节点一定是基环上的节点。
在细节上,对于每个未访问过的节点走 DFS 的结果会存在 3 3 3 种情况:
- 环上节点:刚好走过基环;
- 树链节点:走过树链 + 基环。
- 还有 1 1 1 种情况:DFS 起点是从树链的末端走的,而前面树链的部分和基环都被走过,此时 DFS 终点就不一定是基环节点了。这种情况就同理从终点直接反向遍历就好了,等于说省略了处理基环的步骤。
class Solution {fun countVisitedNodes(edges: List<Int>): IntArray {val n = edges.sizeval ret = IntArray(n)val visit = BooleanArray(n)for (i in 0 until n) {if (visit[i]) continue// DFSval link = LinkedList<Int>()var x = iwhile (!visit[x]) {visit[x] = truelink.add(x)x = edges[x]}if (ret[x] == 0) {val depth = link.size - link.indexOf(x) // (此时 x 位于基环入口)repeat(depth) {ret[link.pollLast()] = depth}}var depth = ret[x]while (!link.isEmpty()) {ret[link.pollLast()] = ++depth}}return ret}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) DFS 都是线性时间;
- 空间复杂度: O ( n ) O(n) O(n) 图空间和队列空间。
推荐阅读
LeetCode 上分之旅系列往期回顾:
- LeetCode 单周赛第 364 场 · 前后缀分解结合单调栈的贡献问题
- LeetCode 单周赛第 363 场 · 经典二分答案与质因数分解
- LeetCode 双周赛第 114 场 · 一道简单的树上动态规划问题
- LeetCode 双周赛第 113 场 · 精妙的 O(lgn) 扫描算法与树上 DP 问题
⭐️ 永远相信美好的事情即将发生,欢迎加入小彭的 Android 交流社群~

相关文章:

LeetCode 周赛上分之旅 #49 再探内向基环树
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。 学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度…...

kubernetes-v1.23.3 部署 kafka_2.12-2.3.0
文章目录 [toc]构建 debian 基础镜像部署 zookeeper配置 namespace配置 gfs 的 endpoints配置 pv 和 pvc配置 configmap配置 service配置 statefulset 部署 kafka配置 configmap配置 service配置 statefulset 这里采用的部署方式如下: 使用自定义的 debian 镜像作为…...

位置编码器
目录 1、位置编码器的作用 2、代码演示 (1)、使用unsqueeze扩展维度 (2)、使用squeeze降维 (3)、显示张量维度 (4)、随机失活张量中的数值 3、定义位置编码器类,我…...
Lua多脚本执行
--全局变量 a 1 b "123"for i 1,2 doc "Holens" endprint(c) print("*************************************1")--本地变量(局部变量) for i 1,2 dolocal d "Holens2"print(d) end print(d)function F1( ..…...
Spirng Cloud Alibaba Nacos注册中心的使用 (环境隔离、服务分级存储模型、权重配置、临时实例与持久实例)
文章目录 一、环境隔离1. Namespace(命名空间):2. Group(分组):3. Services(服务):4. DataId(数据ID):5. 实战演示:5.1 默…...

26663-2011 大型液压安全联轴器 课堂随笔
声明 本文是学习GB-T 26663-2011 大型液压安全联轴器. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了大型液压安全联轴器的分类、技术要求、试验方法及检验规则等。 本标准适用于联接两同轴线的传动轴系,可起到限制…...
ChatGPT架构师:语言大模型的多模态能力、幻觉与研究经验
来源 | The Robot Brains Podcast OneFlow编译 翻译|宛子琳、杨婷 9月26日,OpenAI宣布ChatGPT新增了图片识别和语音能力,使得ChatGPT不仅可以进行文字交流,还可以给它展示图片并进行互动,这是一次ChatGPT向多模态进化的…...

二、VXLAN BGP EVPN基本原理
VXLAN BGP EVPN基本原理 1、BGP EVPN2、BGP EVPN路由2.1、Type2路由——MAC/IP路由2.2、Type3路由——Inclusive Multicast路由2.3、Type5路由——Inclusive Multicast路由 ————————————————————————————————————————————————…...

Evil.js
Evil.js install npm i lodash-utils什么?黑心996公司要让你体统跑路了? 想在离开前给你们的项目留点小礼物? 偷偷地把本项目引入你们的项目吧,你们的项目会有但不仅限于如下的神奇效果: 仅在周日时: 当…...
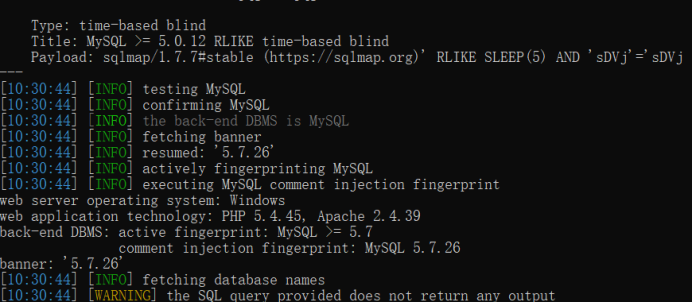
使用sqlmap的 ua注入
文章目录 1.使用sqlmap自带UA头的检测2.使用sqlmap随机提供的UA头3.使用自己写的UA头4.调整level检测 测试环境:bWAPP SQL Injection - Stored (User-Agent) 1.使用sqlmap自带UA头的检测 python sqlmap.py -u http://127.0.0.1:9004/sqli_17.php --cookie“BEEFHOO…...
华为云云耀云服务器L实例评测 | 实例评测使用之体验评测:华为云云耀云服务器管理、控制、访问评测
华为云云耀云服务器L实例评测 | 实例评测使用之体验评测:华为云云耀云服务器管理、控制、访问评测 介绍华为云云耀云服务器 华为云云耀云服务器 (目前已经全新升级为 华为云云耀云服务器L实例) 华为云云耀云服务器是什么华为云云耀…...

resultmap
自定义映射resultMap resultMap处理字段和属性的映射关系 若字段名和实体类中的属性名称不一致,则可以通过resultMap设置自定义映射 建moudel项目【实现多对一、一对多的表操作demo】 temp员工表、dept部门表 导入依赖【mysql驱动、junit、mybatis、日志依赖log4…...
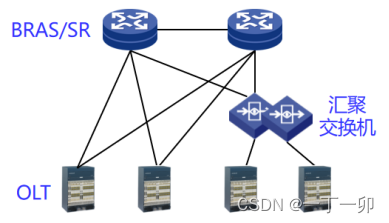
宽带光纤接入网中影响家宽业务质量的常见原因有哪些
1 引言 虽然家宽业务质量问题约60%发生在家庭网(见《家宽用户家庭网的主要质量问题是什么?原因有哪些》一文),但在用户的眼里,所有家宽业务质量问题都是由运营商的网络质量导致的,用户也因此对不同运营商家…...
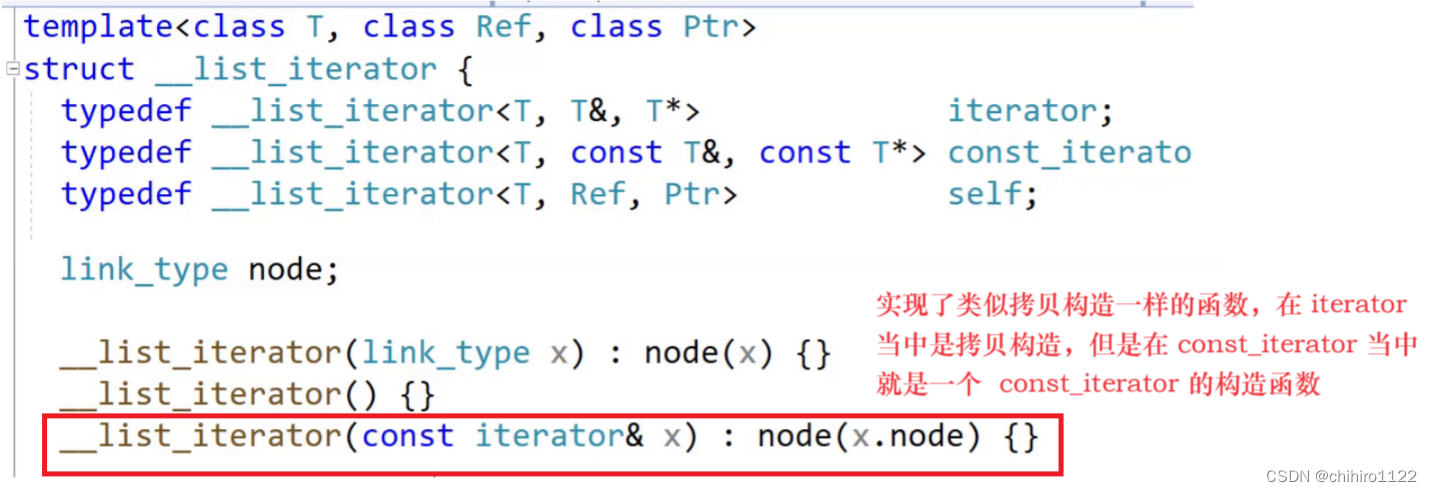
C++ - 封装 unordered_set 和 unordered_map - 哈希桶的迭代器实现
前言 unordered_set 和 unordered_map 两个容器的底层是哈希表实现的,此处的封装使用的 上篇博客当中的哈希桶来进行封装,相当于是在 哈希桶之上在套上了 unordered_set 和 unordered_map 。 哈希桶的逻辑实现: C - 开散列的拉链法&…...
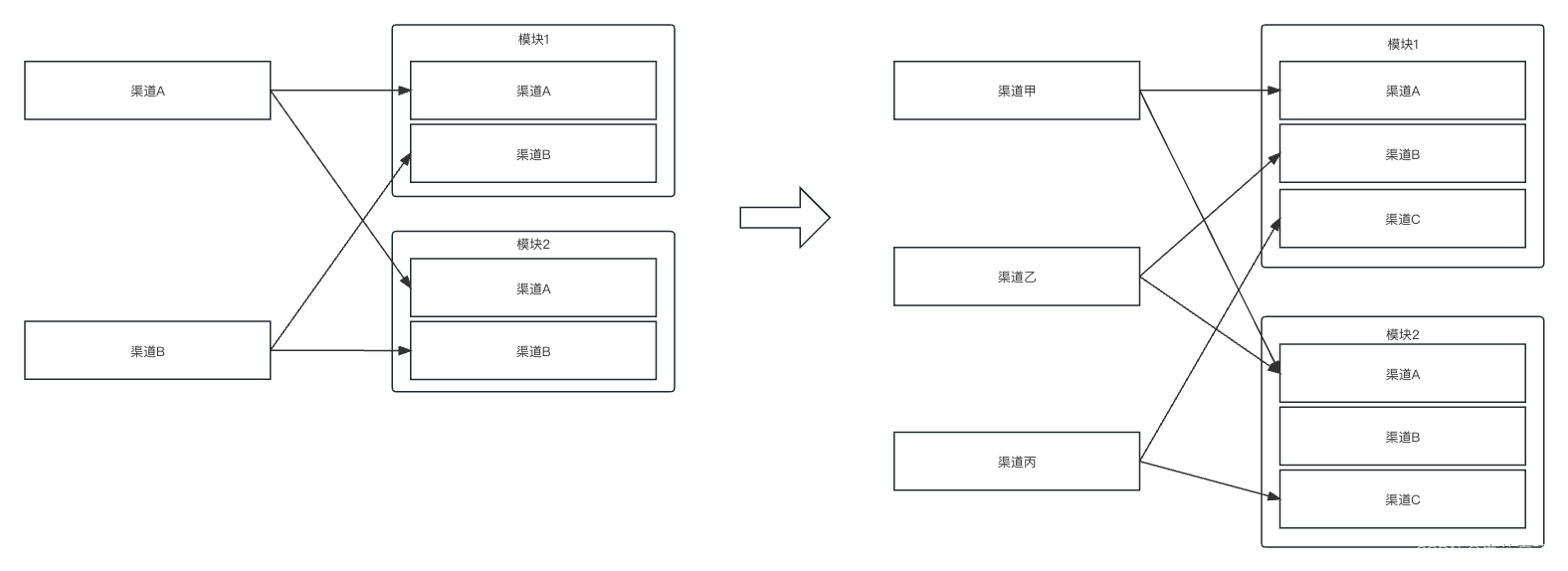
gradle中主模块/子模块渠道对应关系通过配置实现
前言: 我们开发过程中,经常会面对针对不同的渠道,要产生差异性代码和资源的场景。目前谷歌其实为我们提供了一套渠道包的方案,这里简单描述一下。 比如我主模块依赖module1和module2。如果主模块中声明了2个渠道A和B,…...

28383-2012 卷筒料凹版印刷机 学习笔记
声明 本文是学习GB-T 28383-2012 卷筒料凹版印刷机. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了卷筒料凹版印刷机的型式、基本参数、要求、试验方法、检验规则、标志、包装、运输与 贮存。 本标准适用于机组式的卷筒料凹版…...
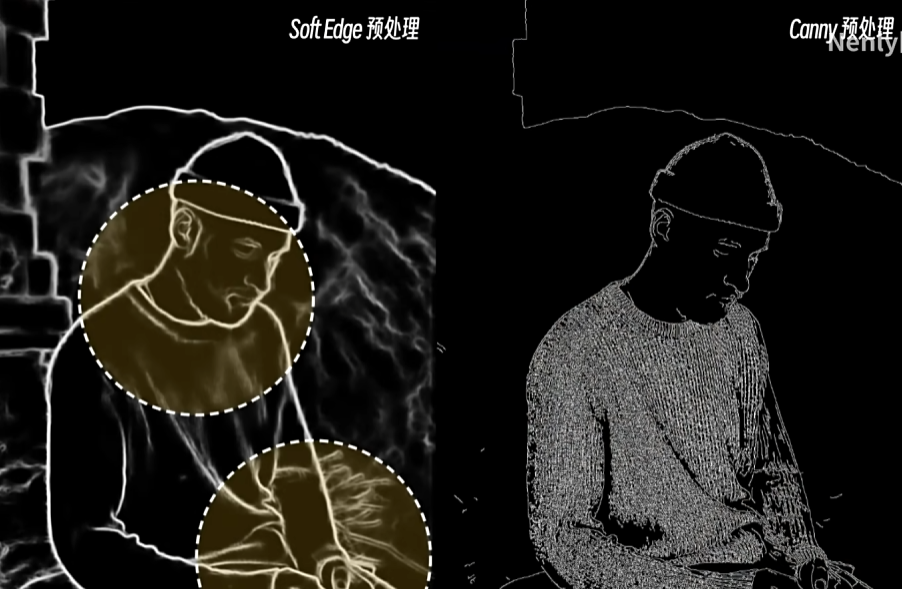
stable diffusion学习笔记【2023-10-2】
L1:界面 CFG Scale:提示词相关性 denoising:重绘幅度 L2:文生图 女性常用的负面词 nsfw,NSFW,(NSFW:2),legs apart, paintings, sketches, (worst quality:2), (low quality:2), (normal quality:2), lowres, normal quality, (…...
flink选择slot
flink选择slot 在这个类里修改 package org.apache.flink.runtime.resourcemanager.slotmanager.SlotManagerImpl; findMatchingSlot(resourceProfile):找到满足要求的slot(负责从哪个taskmanager中获取slot)对应上图第8,9&…...

世界前沿技术发展报告2023《世界信息技术发展报告》(六)网络与通信技术
(六)网络与通信技术 1. 概述2. 5G与光通讯2.1 美国研究人员利用电磁拓扑绝缘体使5G频谱带宽翻倍2.2 日本东京工业大学推出可接入5G网络的高频收发器2.3 美国得克萨斯农工大学通过波束管理改进5G毫米波通信2.4 联发科完成全球首次5G NTN卫星手机连线测试2…...
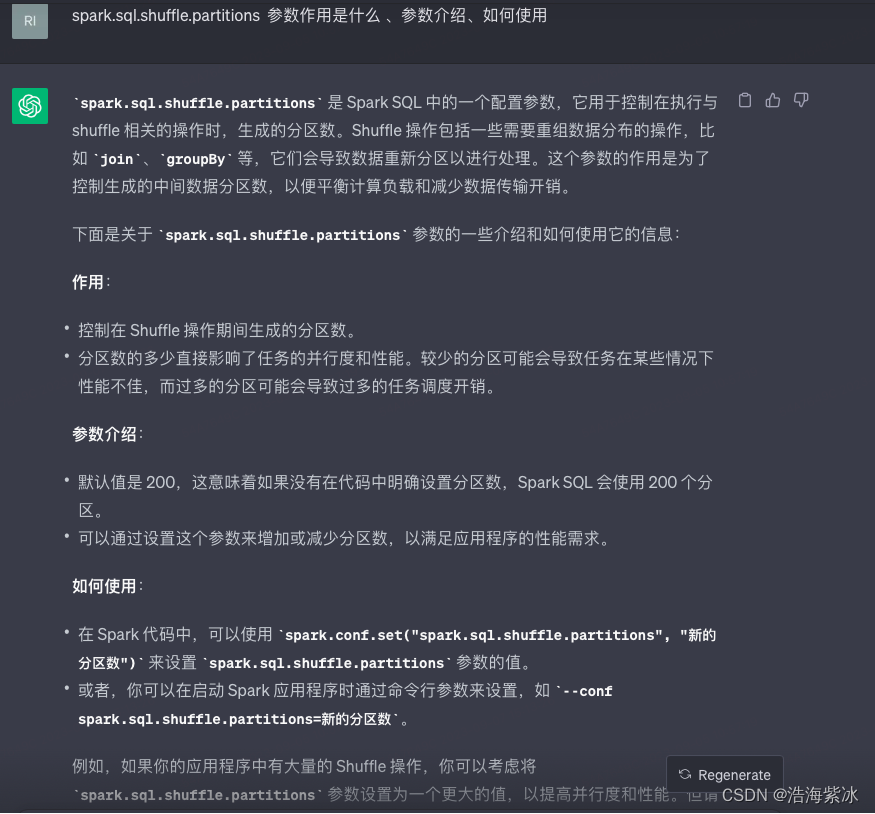
spark SQL 任务参数调优1
1.背景 要了解spark参数调优,首先需要清楚一部分背景资料Spark SQL的执行原理,方便理解各种参数对任务的具体影响。 一条SQL语句生成执行引擎可识别的程序,解析(Parser)、优化(Optimizer)、执行…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
