极大似然估计概念的理解——统计学习方法
目录
1.最大似然估计的概念的理解1
2.最大似然估计的概念的理解2
3.最大似然估计的概念的理解3
4.例子
1.最大似然估计的概念的理解1
最大似然估计是一种概率论在统计学上的概念,是参数估计的一种方法。给定观测数据来评估模型参数。也就是模型已知,参数未定。已知某个随机样本满足某种概率分布,但是其中具体参数不太清楚,参数估计通过若干次的实验,观察其结果,利用结推出参数的大概值。最大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆值把这个参数作为估计的真实值。
最大似然估计是建立在最大似然原理的基础上。最大似然原理:设一个随机实验有若干个可能出现的结果A1、A2、…、An,在一次实验中,结果Ak出现,则认为实验Ak的出现最有利,即Ak出现概率较大。这里用到概率最大概率最可能出现的直观想法,然后对Ak出现的概率公式求极大值,这样便可解未知参数。
最大似然估计定义:最有可能的情况(即找出与样本分布最接近的概率分布模型)
似然函数:它是一种关于统计模型中的参数的函数,表示模型参数的似然性(likelyhood),“似然性”它 与 ("或然性"或 “概率性”或”概率“)意思相近,都是指事件发生的可能性。但是 似然性 和 概率 在统计学中还是有明确的区分:
概率:在参数已知的情况下,预测观测结果;
似然性:在观测结果已知的情况下,对参数进行估值和猜测。
2.最大似然估计的概念的理解2
最大似然估计(Maximum Likelihood Estimation)是一种可以生成拟合数据的任何分布的参数的最可能估计的技术。它是一种解决建模和统计中常见问题的方法——将概率分布拟合到数据集。
例如,假设数据来自泊松(λ)分布,在数据分析时需要知道λ参数来理解数据。这时就可以通过计算MLE找到给定数据的最有可能的λ,并将其用作对参数的良好估计。
MLE是用于拟合或估计数据集概率分布的频率法。这是因为MLE从不计算假设的概率,而贝叶斯解会同时使用数据和假设的概率。MLE假设在计算方法之前,所有的解决方案(分布的参数)都是等可能的,而贝叶斯方法(MAP)不是这样,它使用了关于分布参数的先验信息。
MLE之所以有效,是因为它将寻找数据分布的参数视为一个优化问题。通过最大化似然函数,找到了最可能的解。
3.最大似然估计的概念的理解3
最大似然估计把抽这些样本的每一次抽取看成一个个独立的事件,然后将它们的概率密度乘起来视为一个整体事件A,然后反推“参数为什么值的时候,事件A最有可能发生”
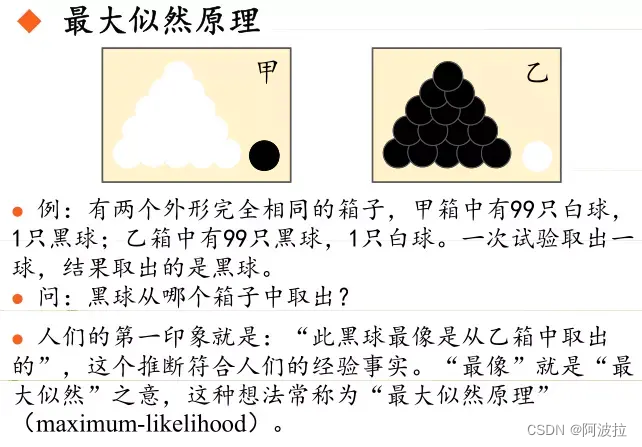
4.例子
假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。我们想知道罐中白球和黑球的比例,现在我们可以每次任意从已经摇匀的罐中拿一个球出来,记录球的颜色,然后把拿出来的球再放回罐中。假如在前面的一百次重复记录中,有七十次是白球,请问罐中白球所占的比例最有可能是多少?
很多人马上就有答案了:70%。而其后的理论支撑是什么呢?
我们假设罐中白球的比例是p,那么黑球的比例就是1-p。因为每抽一个球出来,在记录颜色之后,我们把抽出的球放回了罐中并摇匀,所以每次抽出来的球的颜色服从同一独立分布。
那么问题来了,既然有无数种分布可以选择,极大似然估计应该按照什么原则去选取这个分布呢?
如果第一次抽象的结果记为x1,第二次抽样的结果记为x2....那么样本结果为(x1,x2.....,x100)。这样,我们可以得到如下表达式:
P(样本结果|Model)
= P(x1,x2,…,x100|Model)
= P(x1|Mel)P(x2|M)…P(x100|M)
= p^70(1-p)^30.
答:采取的方法是让这个样本结果出现的可能性最大,也就是使得p^70(1-p)^30值最大,那么我们就可以看成是p的方程,求导即可!
那么既然事情已经发生了,为什么不让这个出现的结果的可能性最大呢?这也就是最大似然估计的核心。
我们想办法让观察样本出现的概率最大,转换为数学问题就是使得:
p^70(1-p)^30最大,这太简单了,未知数只有一个p,我们令其导数为0,即可求出p为70%,与我们一开始认为的70%是一致的。其中蕴含着我们的数学思想在里面。
求最大似然估计的问题,就变成了求似然函数的极值问题。
相关文章:

极大似然估计概念的理解——统计学习方法
目录 1.最大似然估计的概念的理解1 2.最大似然估计的概念的理解2 3.最大似然估计的概念的理解3 4.例子 1.最大似然估计的概念的理解1 最大似然估计是一种概率论在统计学上的概念,是参数估计的一种方法。给定观测数据来评估模型参数。也就是模型已知,参…...

python模拟表格任意输入位置
在表格里输入数值,要任意位置,我找到了好方法: input输入 1. 行 2. 列输入:1 excel每行输入文字input输入位置 3.2 表示输入位置在:3行个列是要实现一个类似于 Excel 表格的输入功能,并且希望能够指定输入…...
如何限制文件只能通过USB打印机打印,限制打印次数和时限并且无法在打印前查看或编辑内容
在今天这个高度信息化的时代,文档打印已经成为日常工作中不可或缺的一部分。然而,这也带来了诸多安全风险,如文档被篡改、知识产权被侵犯以及信息泄露等。为了解决这些问题,只印应运而生。作为一款独特的软件工具,只印…...
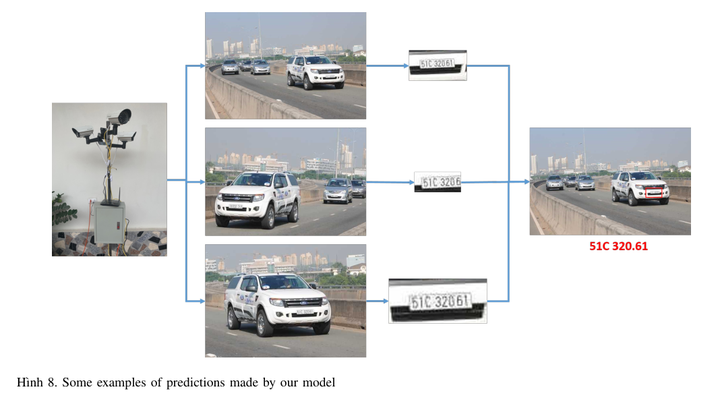
车牌文本检测与识别:License Plate Recognition Based On Multi-Angle View Model
论文作者:Dat Tran-Anh,Khanh Linh Tran,Hoai-Nam Vu 作者单位:Thuyloi University;Posts and Telecommunications Institute of Technology 论文链接:http://arxiv.org/abs/2309.12972v1 内容简介: 1)方向&#x…...

Blender中的4种视图着色模式
Blender中有四种主要的视图着色模式:线框、实体、Look Dev和渲染。它们的主要区别如下: - 线框模式只显示物体的边缘(线框),可以让您看到场景中的所有物体,也可以调整线框的颜色和背景的颜色。 - 实…...
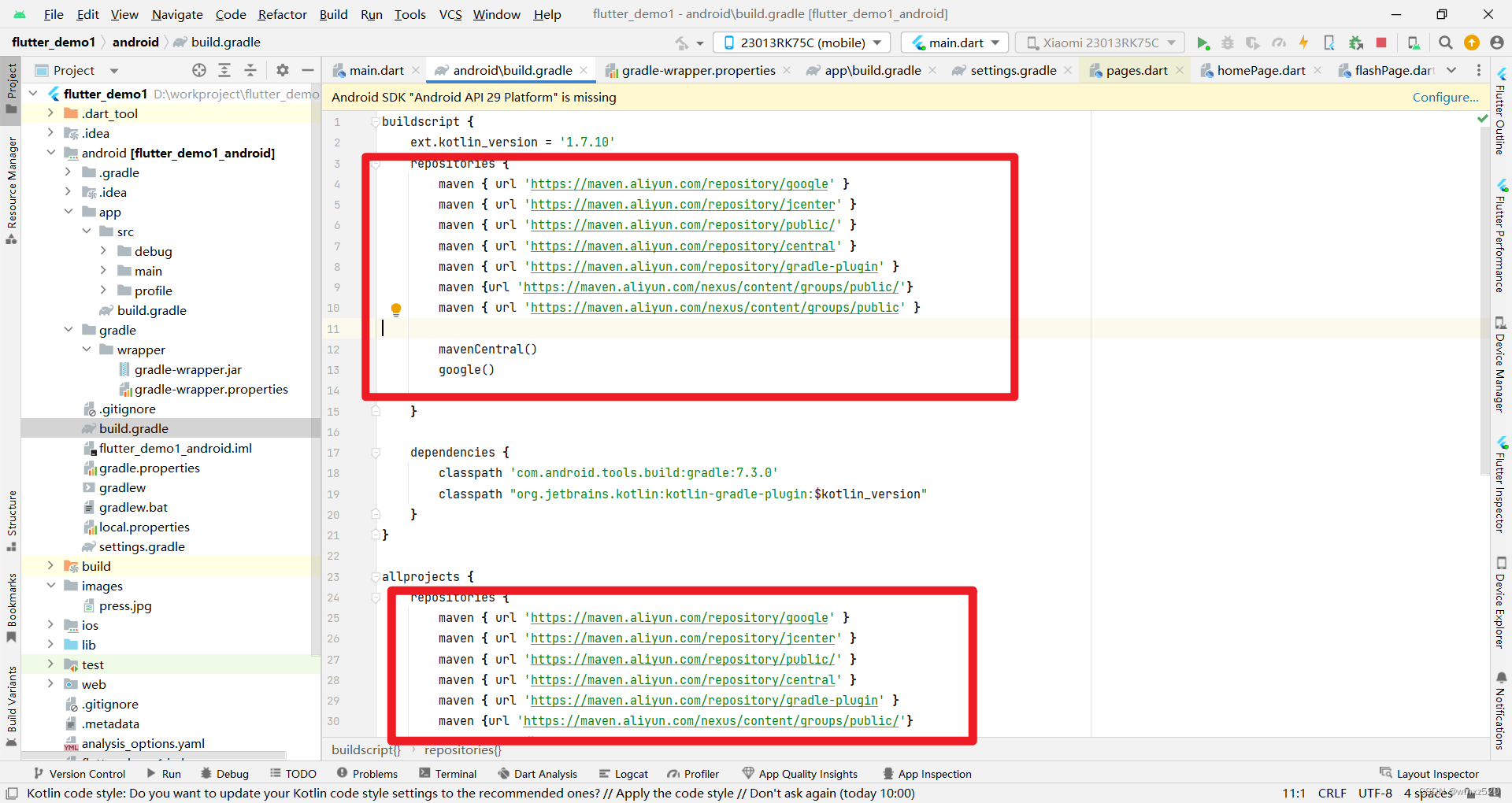
Flutter项目安装到Android手机一直显示在assembledebug
问题 Flutter项目安装到Android手机一直显示在assembledebug 原因 网络不好,gradle依赖下载不下来 解决方案 修改如下的文件 gradle-wrapper.properties 使用腾讯提供的gradle镜像下载 distributionUrlhttps://mirrors.cloud.tencent.com/gradle/gradle-7.5…...
数据预处理【等深分箱与等宽分箱】)
数据挖掘实验(二)数据预处理【等深分箱与等宽分箱】
一、分箱平滑的原理 (1)分箱方法 在分箱前,一定要先排序数据,再将它们分到等深(等宽)的箱中。 常见的有两种分箱方法:等深分箱和等宽分箱。 等深分箱:按记录数进行分箱࿰…...

Vue2 第一次学习
本章为超级浓缩版,文章过于短,方便复习使用哦~ 文章目录 1. 简单引入 vue.js2. 指令2.1 事件绑定指令 v-on (简写 )2.2 内容渲染指令2.3 双向绑定指令 v-model2.4 属性绑定指令 v-bind (简写 : )2.5 条件渲染指令2.6 循环指令 v-for 3. vue 其他知识3.1 侦听器 watch3.2 计算属…...
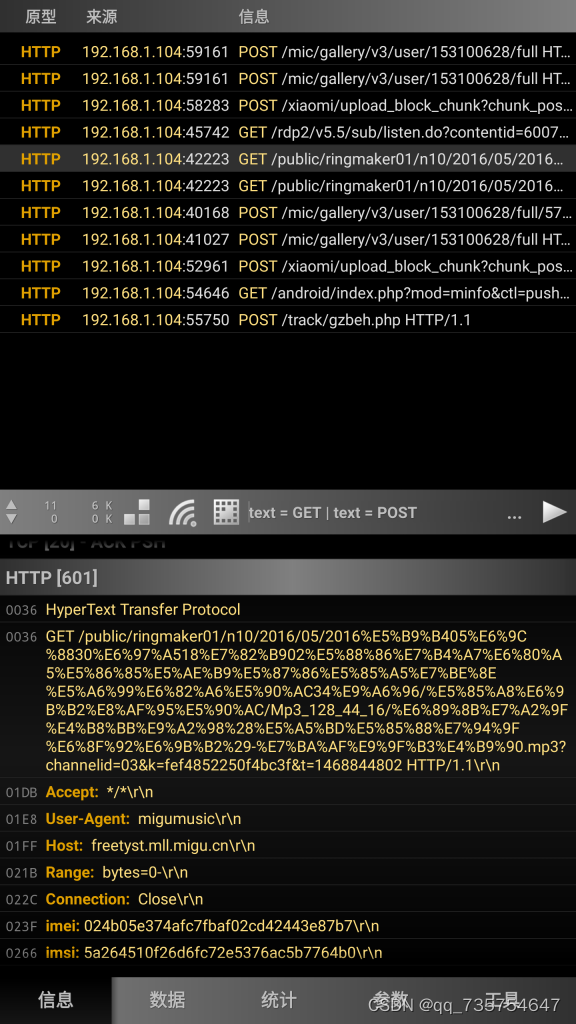
tiny模式基本原理整合
【Tiny模式】的基本构成 M【首头在首位】 U【/】 V【HTTP/】 Host H【真实ip】 XH \r回车 \n换行 \t制表 \ 空格 一个基本的模式构成 [method] [uri] [version]\r\nHost: [host]\r\n[method] [uri] [version]\r\nHost: [host]\r\n 检测顺序 http M H XH 有些地区 XH H M 我这边…...

使用聚氨酯密封件的好处?
聚氨酯密封件因其优异的耐用性、灵活性和广泛的应用范围而在各个行业中广受欢迎。在本文中,我们将探讨使用聚氨酯密封件的优点,阐明其在许多不同领域广泛使用背后的原因。 1、高性能: 聚氨酯密封件具有出色的性能特征,使其成为各…...

DevEco Studio如何安装中文插件
首先 官网下载中文插件 由于DevEco是基于IntelliJ IDEA Community的,所有Compatibility选择“IntelliJ IDEA Community”,然后下载一个对应最新的就ok了。 最后打开Plugins页面,点击右上角齿轮 -> Install Plugin from Disk…。选择下载的…...

10.2 校招 实习 内推 面经
绿泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表格 1、校招 | 国家电网 国网信通产业集团2024届校园招聘! 校招 | 国家电网 国网信通产业集团2024届校园招聘! 2、校招 | 海信集团2024届全球校园招聘正式启动!…...
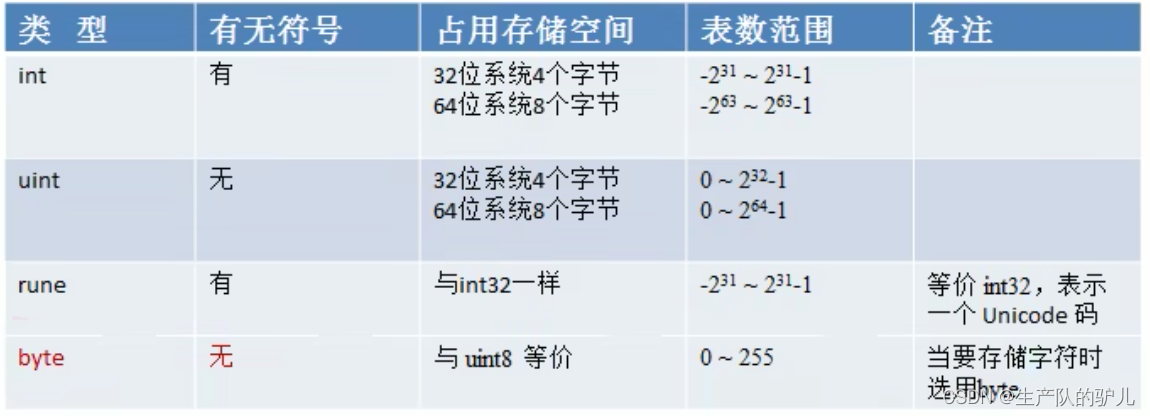
Golang 语言学习 01 包含如何快速学习一门新语言
Golang方向 区块链 go服务器端 (后台流量支撑程序) 支撑主站后台流量(排序,推荐,搜索等),提供负载均衡,cache,容错,按条件分流,统计运行指标 (qps, latenc…...

整理了197个经典SOTA模型,涵盖图像分类、目标检测、推荐系统等13个方向
今天来帮大家回顾一下计算机视觉、自然语言处理等热门研究领域的197个经典SOTA模型,涵盖了图像分类、图像生成、文本分类、强化学习、目标检测、推荐系统、语音识别等13个细分方向。建议大家收藏了慢慢看,下一篇顶会的idea这就来了~ 由于整理的SOTA模型…...
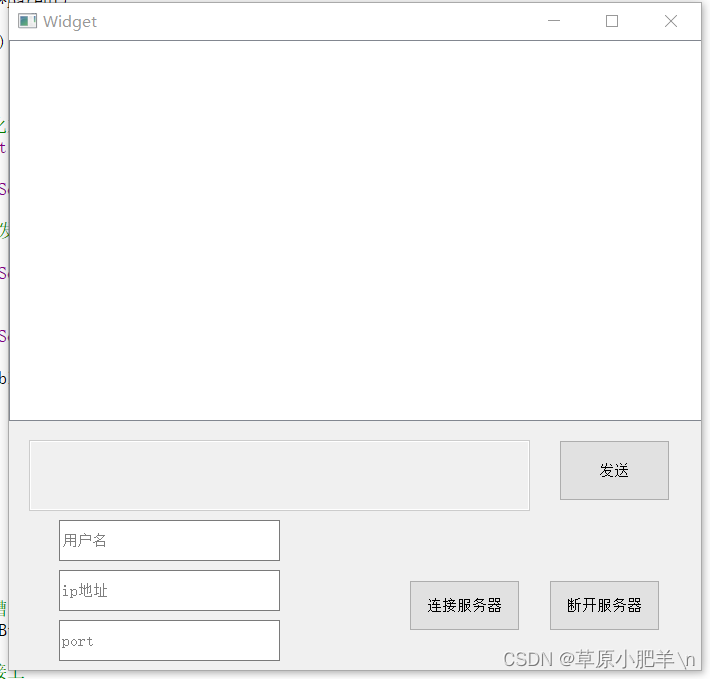
10.4 小任务
目录 QT实现TCP服务器客户端搭建的代码,现象 TCP服务器 .h文件 .cpp文件 现象 TCP客户端 .h文件 .cpp文件 现象 QT实现TCP服务器客户端搭建的代码,现象 TCP服务器 .h文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #includ…...
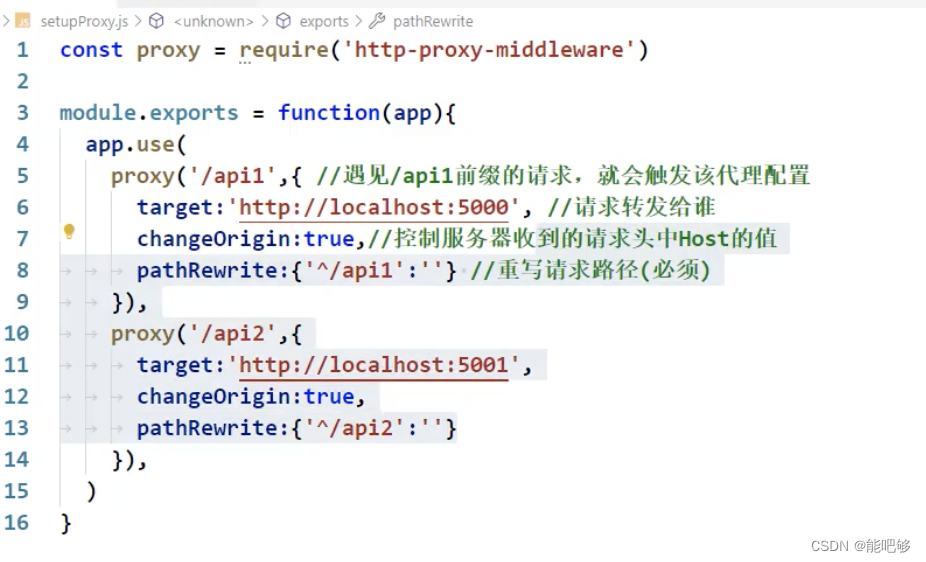
AJAX--Express速成
一、基本概念 1、AJAX(Asynchronous JavaScript And XML),即为异步的JavaScript 和 XML。 2、异步的JavaScript 它可以异步地向服务器发送请求,在等待响应的过程中,不会阻塞当前页面。浏览器可以做自己的事情。直到成功获取响应后…...

开题报告 PPT 应该怎么做
开题报告 PPT 应该怎么做 1、报告时首先汇报自己的姓名、单位、专业和导师。 2、研究背景(2-3张幻灯片) 简要阐明所选题目的研究目的及意义。 研究的目的,即研究应达到的目标,通过研究的背景加以说明(即你为什么要…...

JavaScript系列从入门到精通系列第十四篇:JavaScript中函数的简介以及函数的声明方式以及函数的调用
文章目录 一:函数的简介 1:概念和简介 2:创建一个函数对象 3:调用函数对象 4:函数对象的普通功能 5:使用函数声明来创建一个函数对象 6:使用函数声明创建一个匿名函数 一:函…...
)
当我们做后仿时我们究竟在仿些什么(三)
异步电路之间必须消除毛刺 之前提到过,数字电路后仿的一个主要目的就是动态验证异步电路时序。异步电路的时序是目前STA工具无法覆盖的。 例如异步复位的release是同步事件,其时序是可以靠STA保证的;但是reset是异步事件,它的时序…...

如何将超大文件压缩到最小
1、一个文件目录,查看属性发现这个文件达到了2.50GB; 2、右键此目录选择添加到压缩文件; 3、在弹出的窗口中将压缩文件格式选择为RAR4,压缩方式选择为最好,选择字典大小最大,勾选压缩选项中的创建固实压缩&…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...
