计算机竞赛 题目:基于FP-Growth的新闻挖掘算法系统的设计与实现
文章目录
- 0 前言
- 1 项目背景
- 2 算法架构
- 3 FP-Growth算法原理
- 3.1 FP树
- 3.2 算法过程
- 3.3 算法实现
- 3.3.1 构建FP树
- 3.4 从FP树中挖掘频繁项集
- 4 系统设计展示
- 5 最后
0 前言
🔥 优质竞赛项目系列,今天要分享的是
基于FP-Growth的新闻挖掘算法系统的设计与实现
该项目较为新颖,适合作为竞赛课题方向,学长非常推荐!
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
1 项目背景
如今新闻泛滥,令人眼花缭乱,即使同一话题下的新闻也多得数不胜数。人们可以根据自己的职业和爱好关注专业新闻网站的不同热点要闻。因此,通过对人们关注新闻的热点问题进行分析,可以得出民众对某个领域的关切程度和社会需要解决的问题,也有利于了解当前的舆论焦点,有助于政府了解民意,便于国家对舆论进行正确引导,使我们的社会更加安定和谐。本文以财经领域为例,通过爬虫技术抓取网络上的大量财经新闻,通过对新闻内容文本进行预处理及密度聚类分析来发现热点;从发现的热点中,再进行词汇聚类分析,得出热点所涉及的人或事物,以此分析出社会对经济领域关注的问题和需要解决的问题。

2 算法架构
该项目学长要通过文本挖掘技术进行新闻热点问题分析,把从网上抓取到的财经新闻,通过对新闻内容的聚类,得到新闻热点;再对热点进行分析,通过对某一热点相关词汇的聚类,得到热点问题所涉及的人物、行业或组织等。

1、利用新闻 API、爬虫算法、多线程并行技术,抓取三大专业财经新闻网站(新浪财经、搜狐财经、新华网财经)的大量财经新闻报道;
2、对新闻进行去重、时间段过滤,然后对新闻内容文本进行 jieba
分词并词性标注,过滤出名词、动词、简称等词性,分词前使用自定义的用户词词典增加分词的准确性,分词后使用停用词词典、消歧词典、保留单字词典过滤掉对话题无关并且影响聚类准确性的词,建立每篇新闻的词库,利用
TF-IDF 特征提取之后对新闻进行 DBSCAN 聚类,并对每个类的大小进行排序;
3、针对聚类后的每一类新闻,为了得到该处热点的话题信息,还需要提取它们的标题,利用 TextRank
算法,对标题的重要程度进行排序,用重要性最高的标题来描述该处热点的话题
4、对所有的新闻内容进行 jieba 分词,并训练出 word2vec 词嵌入模型,然后对聚类后的每一类新闻,提取它们的内容分词后的结果,运用
word2vec 模型得到每个词的词向量,再利用 FP-Growth类算法进行相关新闻挖掘。
3 FP-Growth算法原理
3.1 FP树
FP树是一种存储数据的树结构,如下图所示,每一路分支表示数据集的一个项集,数字表示该元素在某分支中出现的次数

3.2 算法过程
1 构建FP树
- 遍历数据集获得每个元素项的出现次数,去掉不满足最小支持度的元素项
- 构建FP树:读入每个项集并将其添加到一条已存在的路径中,若该路径不存在,则创建一条新路径(每条路径是一个无序集合)
2 从FP树中挖掘频繁项集
- 从FP树中获得条件模式基
- 利用条件模式基构建相应元素的条件FP树,迭代直到树包含一个元素项为止
算法过程写得比较简略,具体过程我们在下节的实操中进一步理解。
3.3 算法实现
3.3.1 构建FP树
class treeNode:def __init__(self,nameValue,numOccur,parentNode):self.name=nameValue #节点名self.count=numOccur #节点元素出现次数self.nodeLink=None #存放节点链表中,与该节点相连的下一个元素self.parent=parentNodeself.children={} #用于存放节点的子节点,value为子节点名def inc(self,numOccur):self.count+=numOccurdef disp(self,ind=1):print(" "*ind,self.name,self.count) #输出一行节点名和节点元素数,缩进表示该行节点所处树的深度for child in self.children.values():child.disp(ind+1) #对于子节点,深度+1# 构造FP树# dataSet为字典类型,表示探索频繁项集的数据集,keys为各项集,values为各项集在数据集中出现的次数# minSup为最小支持度,构造FP树的第一步是计算数据集各元素的支持度,选择满足最小支持度的元素进入下一步def createTree(dataSet,minSup=1):headerTable={}#遍历各项集,统计数据集中各元素的出现次数for key in dataSet.keys():for item in key:headerTable[item]=headerTable.get(item,0)+dataSet[key] #遍历各元素,删除不满足最小支持度的元素for key in list(headerTable.keys()):if headerTable[key]<minSup:del headerTable[key]freqItemSet=set(headerTable.keys())#若没有元素满足最小支持度要求,返回None,结束函数if len(freqItemSet)==0:return None,Nonefor key in headerTable.keys():headerTable[key]=[headerTable[key],None] #[元素出现次数,**指向每种项集第一个元素项的指针**]retTree=treeNode("Null Set",1,None) #初始化FP树的顶端节点for tranSet,count in dataSet.items():localD={} #存放每次循环中的频繁元素及其出现次数,便于利用全局出现次数对各项集元素进行项集内排序for item in tranSet:if item in freqItemSet:localD[item]=headerTable[item][0]if len(localD)>0:orderedItems=[v[0] for v in sorted(localD.items(),key=operator.itemgetter(1),reverse=True)] #根据元素全局出现次数对每个项集(tranSet)中的元素进行排序updateTree(orderedItems,retTree,headerTable,count) #使用排序后的项集对树进行填充return retTree,headerTable#树的更新函数#items为按出现次数排序后的项集,是待更新到树中的项集;count为items项集在数据集中的出现次数#inTree为待被更新的树;headTable为头指针表,存放满足最小支持度要求的所有元素def updateTree(items,inTree,headerTable,count):#若项集items当前最频繁的元素在已有树的子节点中,则直接增加树子节点的计数值,增加值为items[0]的出现次数if items[0] in inTree.children: inTree.children[items[0]].inc(count)else:#若项集items当前最频繁的元素不在已有树的子节点中(即,树分支不存在),则通过treeNode类新增一个子节点inTree.children[items[0]]=treeNode(items[0],count,inTree)#若新增节点后表头表中没有此元素,则将该新增节点作为表头元素加入表头表if headerTable[items[0]][1]==None: headerTable[items[0]][1]=inTree.children[items[0]]else:#若新增节点后表头表中有此元素,则更新该元素的链表,即,在该元素链表末尾增加该元素updateHeader(headerTable[items[0]][1],inTree.children[items[0]])#对于项集items元素个数多于1的情况,对剩下的元素迭代updateTreeif len(items)>1:updateTree(items[1::],inTree.children[items[0]],headerTable,count)#元素链表更新函数#nodeToTest为待被更新的元素链表的头部#targetNode为待加入到元素链表的元素节点def updateHeader(nodeToTest,targetNode):#若待被更新的元素链表当前元素的下一个元素不为空,则一直迭代寻找该元素链表的末位元素while nodeToTest.nodeLink!=None: nodeToTest=nodeToTest.nodeLink #类似撸绳子,从首位一个一个逐渐撸到末位#找到该元素链表的末尾元素后,在此元素后追加targetNode为该元素链表的新末尾元素nodeToTest.nodeLink=targetNode测试
#加载简单数据集
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDat#将列表格式的数据集转化为字典格式
def createInitSet(dataSet):retDict={}for trans in dataSet:retDict[frozenset(trans)]=1return retDictsimpDat=loadSimpDat()
dataSet=createInitSet(simpDat)
myFPtree1,myHeaderTab1=createTree(dataSet,minSup=3)
myFPtree1.disp(),myHeaderTab1
输入数据:

由此数据集构建的FP树长这样,看看是不是满足上一节介绍的FP树结构

3.4 从FP树中挖掘频繁项集
具体过程如下:
1 从FP树中获得条件模式基
- 条件模式基:以所查找元素项为结尾的路径集合,每条路径都是一条前缀路径,路径集合包括前缀路径和路径计数值。
- 例如,元素"r"的条件模式基为 {x,s}2,{z,x,y}1,{z}1
- 前缀路径:介于所查找元素和树根节点之间的所有内容
- 路径计数值:等于该条前缀路径的起始元素项(即所查找的元素)的计数值
2 利用条件模式基构建相应元素的条件FP树
- 对每个频繁项,都要创建一棵条件FP树。
- 例如对元素t创建条件FP树:使用获得的t元素的条件模式基作为输入,利用构建FP树相同的逻辑构建元素t的条件FP树
3 迭代步骤(1)(2),直到树包含一个元素项为止
-
接下来继续构建{t,x}{t,y}{t,z}对应的条件FP树(tx,ty,tz为t条件FP树的频繁项集),直到条件FP树中没有元素为止
-
至此可以得到与元素t相关的频繁项集,包括2元素项集、3元素项集。。。
#由叶节点回溯该叶节点所在的整条路径 #leafNode为叶节点,treeNode格式;prefixPath为该叶节点的前缀路径集合,列表格式,在调用该函数前注意prefixPath的已有内容 def ascendTree(leafNode,prefixPath):if leafNode.parent!=None:prefixPath.append(leafNode.name)ascendTree(leafNode.parent,prefixPath)#获得指定元素的条件模式基 #basePat为指定元素;treeNode为指定元素链表的第一个元素节点,如指定"r"元素,则treeNode为r元素链表的第一个r节点 def findPrefixPath(basePat,treeNode):condPats={} #存放指定元素的条件模式基while treeNode!=None: #当元素链表指向的节点不为空时(即,尚未遍历完指定元素的链表时)prefixPath=[]ascendTree(treeNode,prefixPath) #回溯该元素当前节点的前缀路径if len(prefixPath)>1:condPats[frozenset(prefixPath[1:])]=treeNode.count #构造该元素当前节点的条件模式基treeNode=treeNode.nodeLink #指向该元素链表的下一个元素return condPats#有FP树挖掘频繁项集 #inTree: 构建好的整个数据集的FP树 #headerTable: FP树的头指针表 #minSup: 最小支持度,用于构建条件FP树 #preFix: 新增频繁项集的缓存表,set([])格式 #freqItemList: 频繁项集集合,list格式def mineTree(inTree,headerTable,minSup,preFix,freqItemList):#按头指针表中元素出现次数升序排序,即,从头指针表底端开始寻找频繁项集bigL=[v[0] for v in sorted(headerTable.items(),key=lambda p:p[1][0])] for basePat in bigL:#将当前深度的频繁项追加到已有频繁项集中,然后将此频繁项集追加到频繁项集列表中newFreqSet=preFix.copy()newFreqSet.add(basePat)print("freqItemList add newFreqSet",newFreqSet)freqItemList.append(newFreqSet)#获取当前频繁项的条件模式基condPatBases=findPrefixPath(basePat,headerTable[basePat][1])#利用当前频繁项的条件模式基构建条件FP树myCondTree,myHead=createTree(condPatBases,minSup)#迭代,直到当前频繁项的条件FP树为空if myHead!=None:mineTree(myCondTree,myHead,minSup,newFreqSet,freqItemList)
接着刚才构建的FP树,测试一下,
freqItems=[]
mineTree(myFPtree1,myHeaderTab1,3,set([]),freqItems)
freqItems
我们从FP树中挖掘到的频繁项集如下,这里设置的最小支持度为3:

上图表示数据集中,支持度大于3(出现3次以上)的元素项集,即,频繁项集。
4 系统设计展示
为了方便操作及理解,学长使用 Python 的 tkinter 模块设计了一个系统操作界面

分析可视化




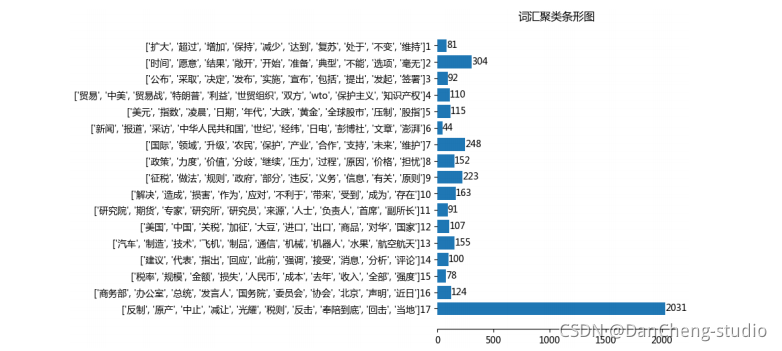
(未完待续。。。。)
5 最后
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
相关文章:

计算机竞赛 题目:基于FP-Growth的新闻挖掘算法系统的设计与实现
文章目录 0 前言1 项目背景2 算法架构3 FP-Growth算法原理3.1 FP树3.2 算法过程3.3 算法实现3.3.1 构建FP树 3.4 从FP树中挖掘频繁项集 4 系统设计展示5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 基于FP-Growth的新闻挖掘算法系统的设计与实现…...

String 类型的变量和常量做 “+” 运算时发生了什么?
先看看字符串不加 final 关键字拼接的情况(jdk1.8): String str1 "str" String str2 "ing" String str3 "str" "ing" String str4 str1 str2 String str5 "string" System.out.println(str3 …...

【Java互联网技术】MinIO分布式文件存储服务
应用场景 互联网海量非结构化数据的存储 基本概念 Object:存储的基本对象,如文件、字节流等 Bucket:存储Object的逻辑空间,相当于顶层文件夹 Drive:存储数据的磁盘,在MinIO启动时,以参数的…...
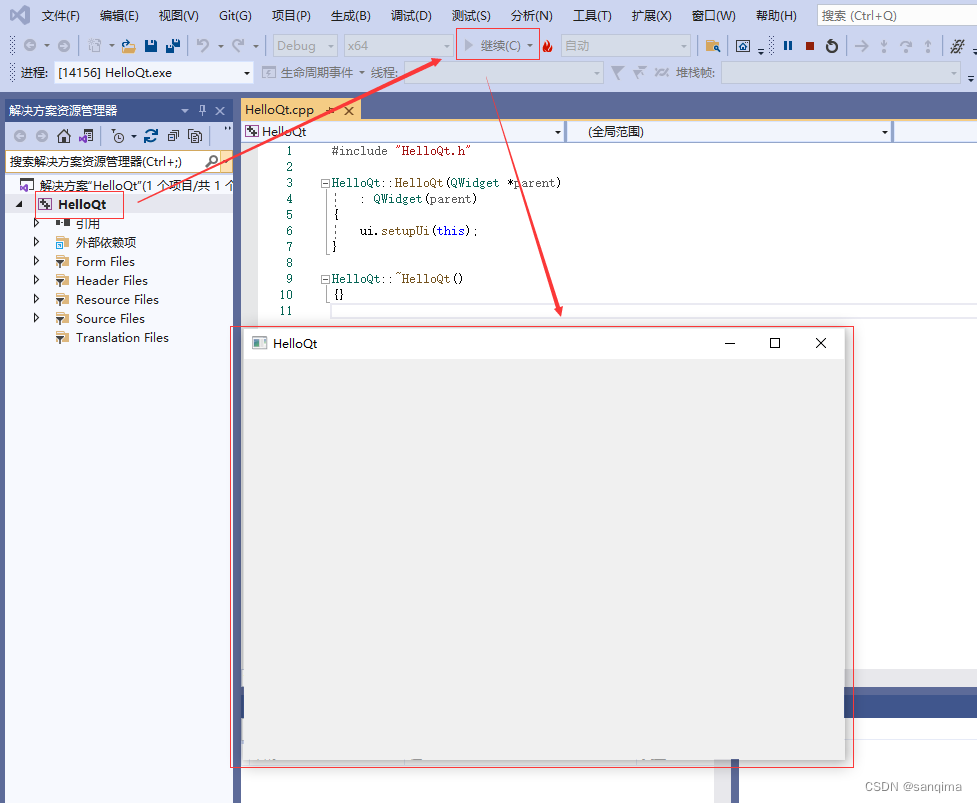
在visual studio里配置Qt插件并运行Qt工程
Qt插件,也叫qt-vsaddin,它以*.vsix后缀名结尾。visual studio简称为VS,从visual studio 2010版本开始,VS支持Qt框架的开发,Qt以插件方式集成到VS里。这里简述在visual studio 2019里配置Qt 5.14.2插件,并配…...

【C语言】利用数组处理批量数据(字符数组)
前言:前面已经介绍了,字符数据是以字符的ASCII代码存储在存储单元中的,一般占一个字节。由于ASCII代码也属于整数形式,因此在C99标准中,把字符类型归纳为整型类型中的一种。 💖 博主CSDN主页:卫卫卫的个人主页 &#x…...

算法通过村第十二关-字符串|白银笔记|经典面试题
文章目录 前言1. 反转问题1.1 反转字符串1.2 k个一组反转1.3 仅仅反转字母1.3.1 采用栈实现操作1.3.2 采用双指针实现操作 1.4 反转字符串里面的单词1.4.1 使用语言提供的方法来解决(内置API)1.4.2 如何优雅自己实现上述功能 2. 验证回文串3. 字符串中的第一个唯一字符4. 判断是…...
《视觉 SLAM 十四讲》V2 第 5 讲 相机与图像
文章目录 相机 内参 && 外参5.1.2 畸变模型单目相机的成像过程5.1.3 双目相机模型5.1.4 RGB-D 相机模型 实践5.3.1 OpenCV 基础操作 【Code】OpenCV版本查看 5.3.2 图像去畸变 【Code】5.4.1 双目视觉 视差图 点云 【Code】5.4.2 RGB-D 点云 拼合成 地图【Code】 习题题…...
)
使用libmodbus库开发modbusTcp从站(支持多个主站连接)
使用libmodbus库开发modbusTcp从站(支持多个主站连接) Chapter1 使用libmodbus库开发modbusTcp从站(支持多个主站连接)rdsmodbusslave.hrdsmodbusslave.cppmain.cpp Chapter1 使用libmodbus库开发modbusTcp从站(支持多个主站连接) 参考链接:…...
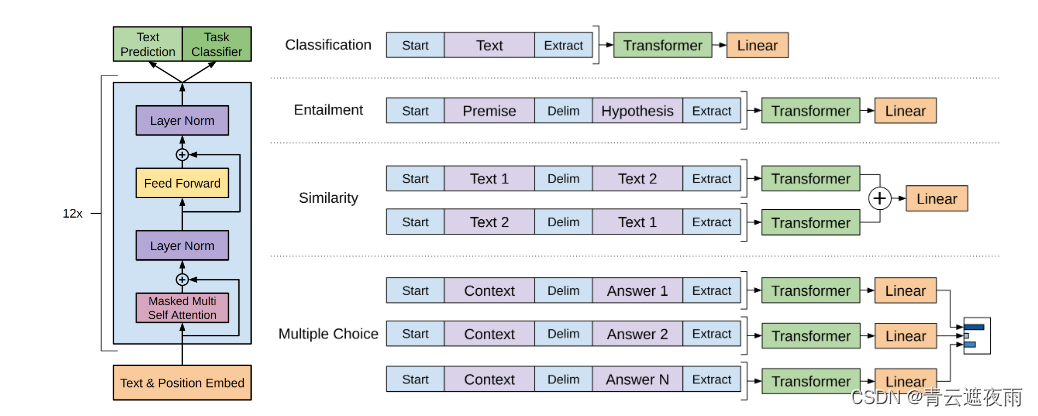
GPT系列论文解读:GPT-2
GPT系列 GPT(Generative Pre-trained Transformer)是一系列基于Transformer架构的预训练语言模型,由OpenAI开发。以下是GPT系列的主要模型: GPT:GPT-1是于2018年发布的第一个版本,它使用了12个Transformer…...
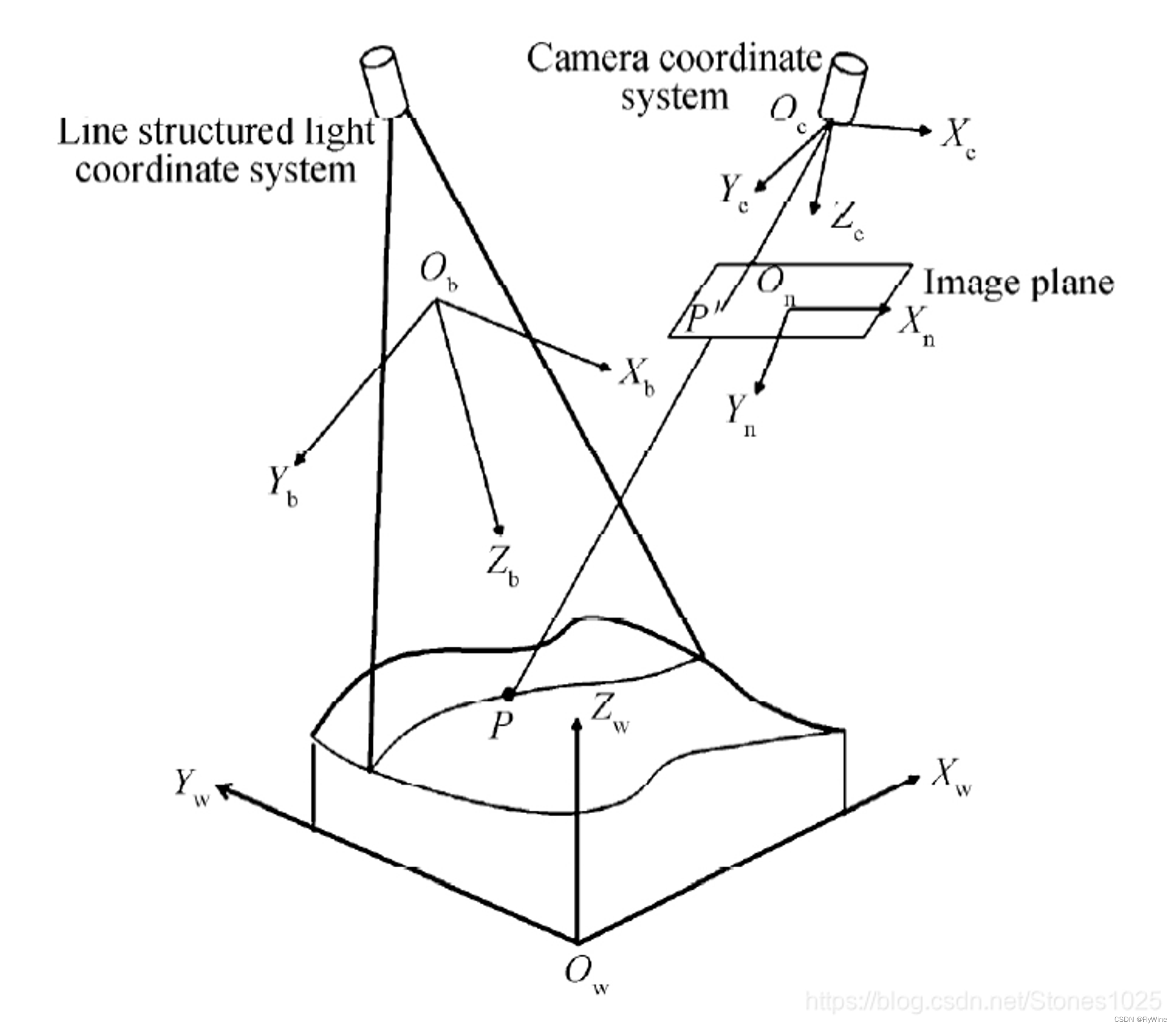
(四)激光线扫描-光平面标定
在上一章节,已经实现了对激光线条的中心线提取,并且在最开始已经实现了对相机的标定,那么相机标定的作用是什么呢? 就是将图像二维点和空间三维点之间进行互相转换。 1. 什么是光平面 激光发射器投射出一条线,形成的一个扇形区域平面就是光平面,也叫光刀面,与物体相交…...
妙不可言的Python之旅----(二)
Python基础语法 什么是字面量 字面量:在代码中,被写下来的的固定的值,称之为字面量 常用的值类型 类型 描述 说明 数字(Number) 支持 • 整数(int) • 浮点数(floatÿ…...

cartographer(1)-运行
1.下载数据集 #1.下载数据集: mkdir /home/tang/bagfiles#2.开始二维建图 cd /home/tang/carto_ws/cartographer_detailed_comments_ws/install_isolated/source install_isolated/setup.bash rospack profile #新装的包索引地址存在ros的环境里 roslaunch ca…...

C++:模板进阶与继承
模板进阶与继承 模板进阶1.非类型的模板参数2.模板的特化2.1特化的概念2.2函数模板特化2.3类模板特化2.4全特化和偏特化2.4.1全特化2.4.2偏特化 3.模板的分离编译3.1同文件分离3.2不同文件下分离 继承1.继承的概念和定义1.1继承的概念1.2继承的定义1.2.1定义格式1.2.2继承关系和…...

vue-img-cutter 实现图片裁剪[vue 组件库]
借助 vue-img-cutter 可以在网页端实现图片裁剪功能,最终功能效果如下: 组件 npm 安装 npm install vue-img-cutter2 --save-dev # for vue2 npm install vue-img-cutter3 --save-dev # for vue3vue-img-cutter使用 template模板标签模块,…...

手把手教你从零开始腾讯云服务器部署(连接建站教程)
使用腾讯云服务器搭建网站全流程,包括轻量应用服务器和云服务器CVM建站教程,轻量可以使用应用镜像一键建站,云服务器CVM可以通过安装宝塔面板的方式来搭建网站,腾讯云服务器网txyfwq.com分享使用腾讯云服务器建站教程,…...
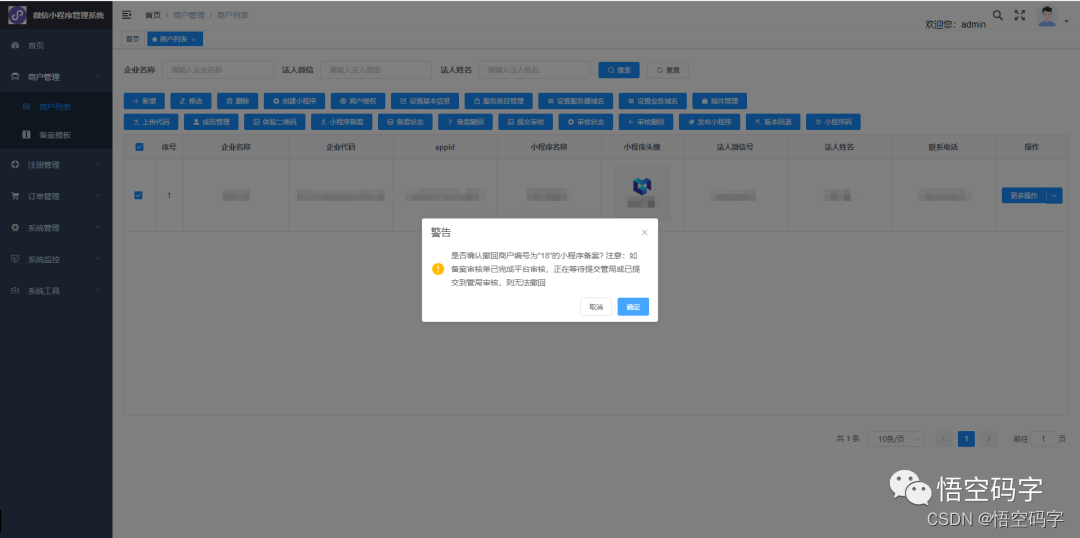
微信开放平台第三方开发,实现代小程序备案申请
大家好,我是小悟 微信小程序备案整体流程总共分为五个环节:备案信息填写、平台初审、工信部短信核验、通管局审核和备案成功。 服务商可以代小程序发起备案申请。在申请小程序备案之前,需要确保小程序基本信息已填写完成、小程序至少存在一个…...

设计模式——11. 享元模式
1. 说明 享元模式(Flyweight Pattern)是一种结构型设计模式,它旨在减少系统中相似对象的内存占用或计算开销,通过共享相同的对象来达到节省资源的目的。 享元模式的核心思想是将对象的状态分为内部状态(Intrinsic State)和外部状态(Extrinsic State): 内部状态是对象…...

【LLM】主流大模型体验(文心一言 科大讯飞 字节豆包 百川 阿里通义千问 商汤商量)
note 智谱AI体验百度文心一言体验科大讯飞大模型体验字节豆包百川智能大模型阿里通义千问商汤商量简要分析:仅从测试“老婆饼为啥没有老婆”这个问题的结果来看,chatglm分点作答有条理(但第三点略有逻辑问题);字节豆包…...
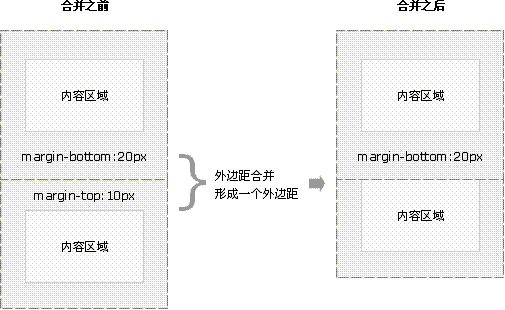
CSS小计
1:设置图片随窗缩放 使用百分比 width: 100%;height: 100%; 使用vmin: 将可视区域分为100vmin width: 100vmin;height: 100vmin; 2:设置字体颜色与背景色融合 mix-blend-mode: difference 3: 设置宽度自适应 width:fit-content 4:外边距合并 当两个相领的两个容…...
机器学习:决策树
决策树 决策树是一种基于树形结构的模型,决策树从根节点开始,一步步走到叶子节点(决策),所有的数据最终都会落到叶子节点,既可以做分类也可以做回归。 特征选择 根节点的选择该用哪一个特征呢ÿ…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
