【算法挨揍日记】day16——525. 连续数组、1314. 矩阵区域和

525. 连续数组
525. 连续数组
题目描述:
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。

解题思路:
本题的元素只有0和1,根据题目意思,我们可以把题目看成找一段最长的子区间使得区间的0
和1的数量相同,我们可以对其优化将所有的0变成-1,这样这段区间的和就为0
也就是转化为在【0,i-1】这个区间内最长的和为0的子数组
我们依旧可以利用哈希表hash,我们还得处理一下默认前缀和为0的时候等于-1的时候
长度的计算:

解题思路:
class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int,int>hash;hash[0]=-1;int ret=0,sum=0;for(int i=0;i<nums.size();i++){sum+=nums[i]==0?-1:1;if(hash.count(sum))ret=max(ret,i-hash[sum]);else hash[sum]=i;}return ret;}
};1314. 矩阵区域和
1314. 矩阵区域和
题目描述:
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
i - k <= r <= i + k,j - k <= c <= j + k且(r, c)在矩阵内。
解题思路:
本题我们还是使用前缀和+哈希表,不过是二维前缀和
因为本题的计算的下标的范围可能会越界,因此我们可以min和max函数就行解决,这里的+1是因为需要进行下标匹配,下标匹配下面会讲;
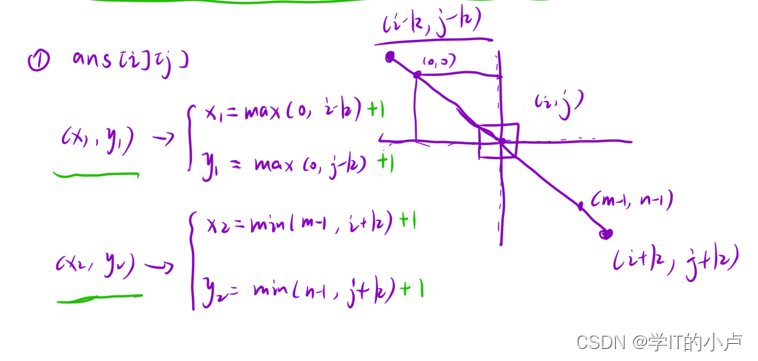
有个细节需要注意就是:
我们的mat数组是从0开始的,而我们的前缀和数组dp是从1开始,而我们返回的数组ans是从0开始的
因为力扣进行结果判断的时候需要从0开始,不然本题更加简单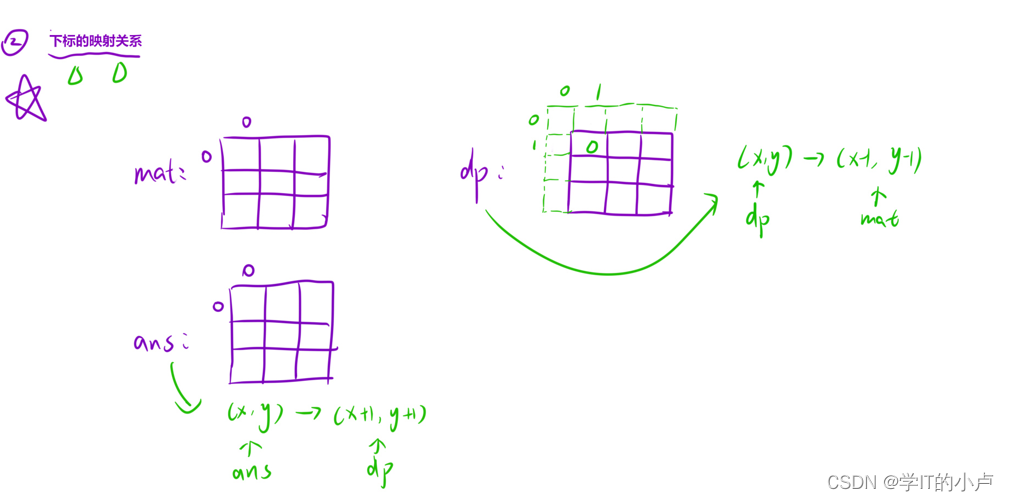
解题代码:
class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int n=mat.size();int m=mat[0].size();vector<vector<int>> dp(n+1,vector<int>(m+1));for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];vector<vector<int>> ans(n,vector<int>(m));for(int i=0;i<n;i++){for(int j=0;j<m;j++){int x1=max(0,i-k)+1;int y1=max(0,j-k)+1;int x2=min(n-1,i+k)+1;int y2=min(m-1,j+k)+1;ans[i][j]=dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1];}}return ans;}
};相关文章:
【算法挨揍日记】day16——525. 连续数组、1314. 矩阵区域和
525. 连续数组 525. 连续数组 题目描述: 给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。 解题思路: 本题的元素只有0和1,根据题目意思,我们可以把题目看成找一段最…...
k8s-13 存储之secret
Secret 对象类型用来保存敏感信息,例如密码、OAuth 令牌和 ssh key。 敏感信息放在 secret 中比放在 Pod 的定义或者容器镜像中来说更加安全和灵活 。 Pod 可以用两种方式使用 secret:作为 volume 中的文件被挂载到 pod 中的一个或者多个容器里 当 kubelet 为 pod 拉…...
)
什么是高阶成分(HOC)
高阶组件(Higher-Order Component,HOC)是一种在React中用于组件复用和逻辑抽象的设计模式。它本质上是一个函数,接受一个组件作为参数,并返回一个新的组件。 1. HOC的作用: HOC允许我们在不修改原始组件的…...

深度学习硬件配置推荐
目录 1. 基础推荐2. GPU显存与内存是一个1:4的配比?3. deep learning 入门和kaggle比赛4. 有些 Kaggle 比赛数据集很大,可能需要更多的 GPU 显存,请推荐显存4. GDDR6和HBM25. HDD 或 SATA SSD1. 基础推荐 假设您作为一个深度学习入门学者的需求,以下是一份推荐的电脑硬件配…...
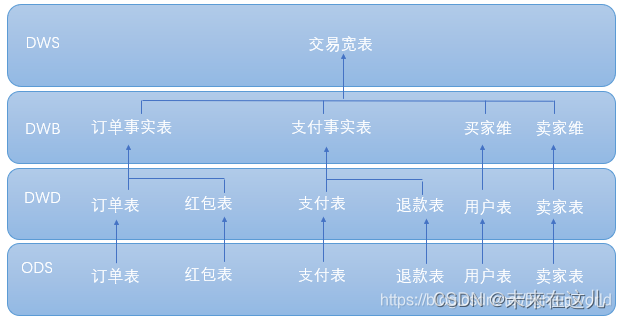
数仓建设(一)
想了想,我们的数仓的建设是基于大数据平台进行的,中间也经历了比较曲折的过程。 每个行业都有自身的业务区别,不过很多还是比较相通的。 本文将全面讲解数仓建设规范,从数据模型规范,到数仓公共规范,数仓各…...

Springboot整合taos时序数据库TDengine
1.首先安装TDengine服务端在linux上 TDengine多种安装包的安装和卸载 - TDengine | 涛思数据安装过程直接去官网看,非常详细简单 2.出现的问题 windows连接 invalid app version 版本不对应 版本不对应的问题,需要在linux上安装的版本和windows client版本一致,不然w…...
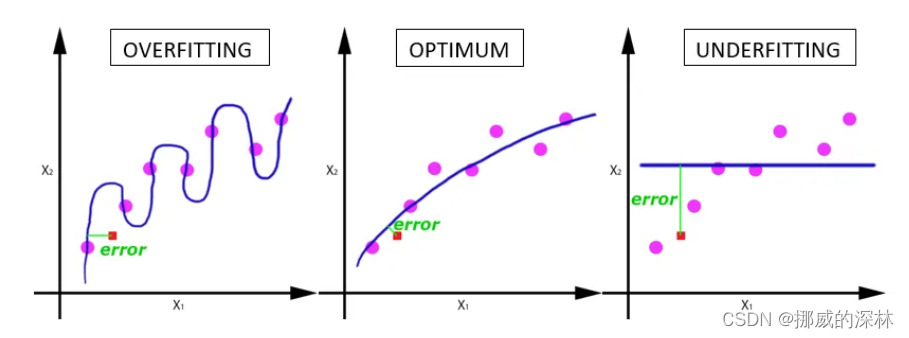
Epoch、批量大小、迭代次数
梯度下降 它是 机器学习中使用的迭代 优化算法,用于找到最佳结果(曲线的最小值)。 坡度 是指 斜坡的倾斜度或倾斜度 梯度下降有一个称为 学习率的参数。 正如您在上图(左)中看到的,最初步长较大&#…...

qt-C++笔记之清空QVBoxLayout中的QCheckBox
qt-C笔记之清空QVBoxLayout中的QCheckBox QVBoxLayout 和 QCheckBox 是两个类,都是 PyQt/PySide 中用于创建图形用户界面 (GUI) 的工具。它们通常与 Qt 库一起使用,Qt 是一个流行的跨平台 GUI 库,可以用于创建桌面应用程序。 QVBoxLayout: Q…...

pc微信39223部分算法call偏移
WechatWin.dll 基址:78FD0000 MD5_Init_call 7AF48C80 | 56 | push esi | 7AF48C81 | 8B7424 08 | mov esi,dword ptr ss:[esp0x8] | 7AF48C85 | 6A 4C | push 0x4C …...
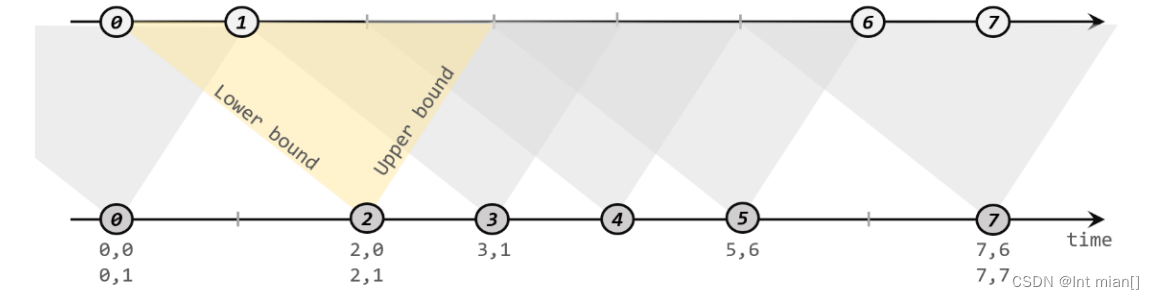
尚硅谷Flink(三)时间、窗口
1 🎰🎲🕹️ 🎰时间、窗口 🎲窗口 🕹️是啥 Flink 是一种流式计算引擎,主要是来处理无界数据流的,数据源源不断、无穷无尽。想要更加方便高效地处理无界流,一种方式就…...

MPLS基础
1. MPLS原理与配置 MPLS基础 (1)MPLS概念 MPLS位于TCP/IP协议栈中的数据链路层和网络层之间,可以向所有网络层提供服务。 通过在数据链路层和网络层之间增加额外的MPLS头部,基于MPLS头部实现数据快速转发。 本课程仅介绍MPLS在…...

react+antd+Table实现表格初始化勾选某条数据,分页切换保留上一页勾选的数据
加上rowKey这个属性 <Table rowKey{record > record.id} // 加上rowKey这个属性rowSelection{rowSelection}columns{columns}dataSource{tableList}pagination{paginationProps} />...

Linux shell编程学习笔记13:文件测试运算
Linux Shell 脚本编程和其他编程语言一样,支持算数、关系、布尔、逻辑、字符串、文件测试等多种运算。前面几节我们依次研究了 Linux shell编程 中的 字符串运算、算术运算、关系运算、布尔运算 和 逻辑运算,今天我们来研究 Linux shell编程中的文件测…...

element ui this.$msgbox 自定义组件
this.$msgbox({title: "选择", message: (<com1figs{this.figs} on-selected{this.new_selected}></com1>),showCancelButton: false,showConfirmButton: false,}); 运行报错 Syntax Error: Unexpected token (89:20) 参考: https://gith…...
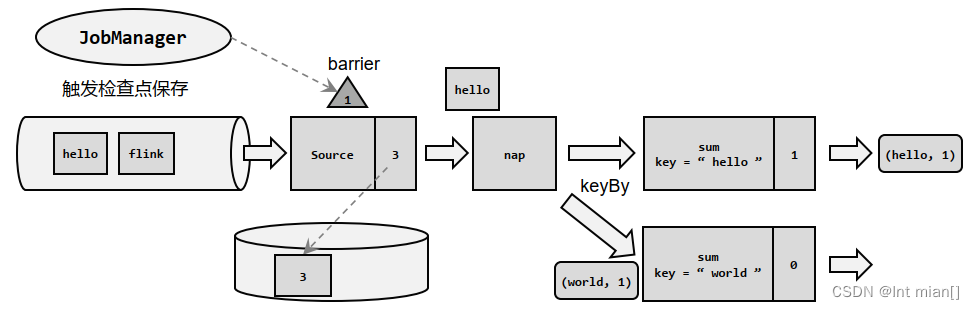
尚硅谷Flink(四)处理函数
目录 🦍处理函数 🐒基本处理函数 🐒按键分区处理函数(KeyedProcessFunction) 🐵定时器(Timer)和定时服务(TimerService) // 1、事件时间的案例 // 2、处理…...
AXURE RP EXTENSION For Chrome 安装
在浏览器上输入地址:chrome://extensions/ 打开图片中这个选项,至此你就能通过index.html访问...
-3)
24、Flink 的table api与sql之Catalogs(java api操作视图)-3
Flink 系列文章 1、Flink 部署、概念介绍、source、transformation、sink使用示例、四大基石介绍和示例等系列综合文章链接 13、Flink 的table api与sql的基本概念、通用api介绍及入门示例 14、Flink 的table api与sql之数据类型: 内置数据类型以及它们的属性 15、Flink 的ta…...
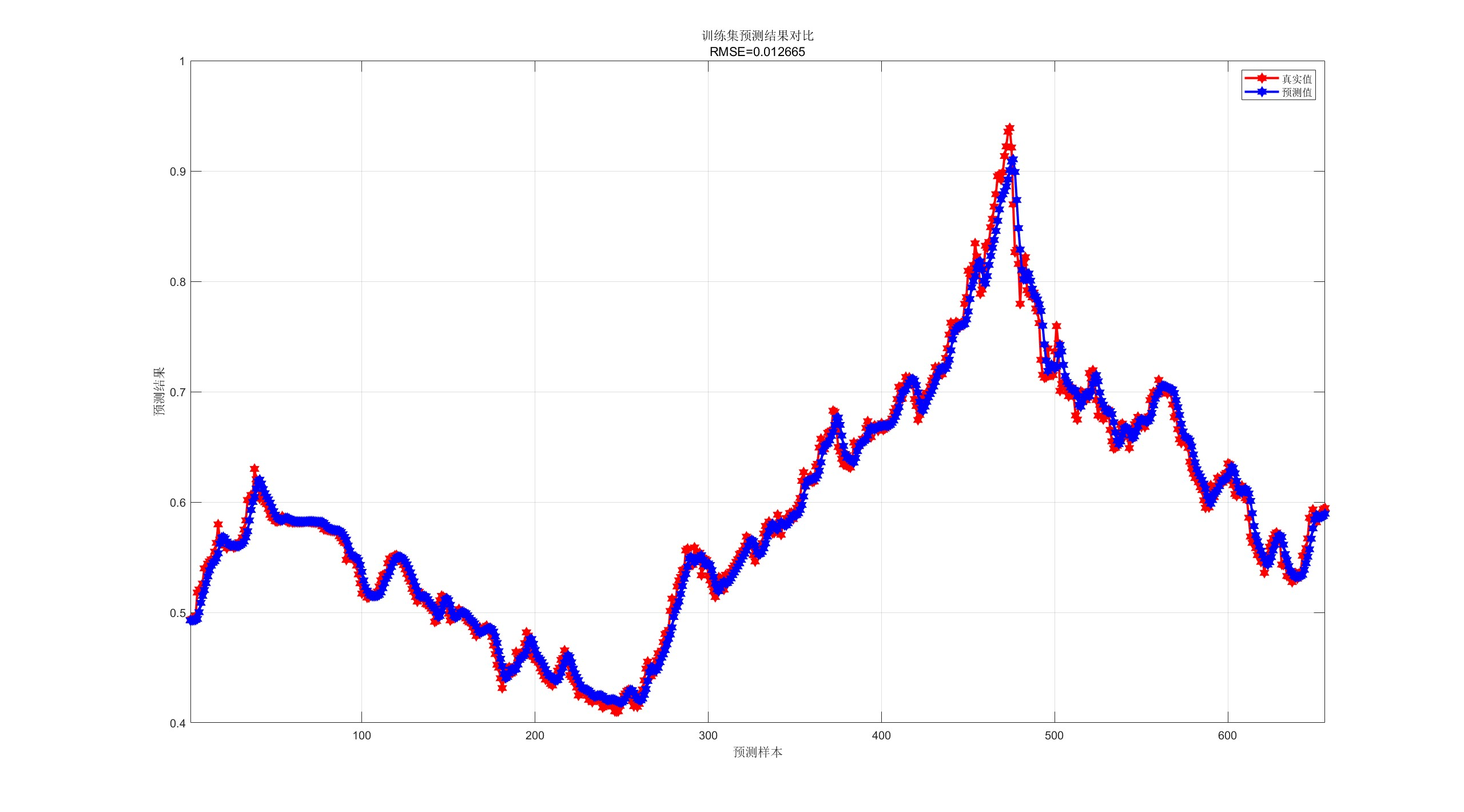
【CNN-GRU预测】基于卷积神经网络-门控循环单元的单维时间序列预测研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
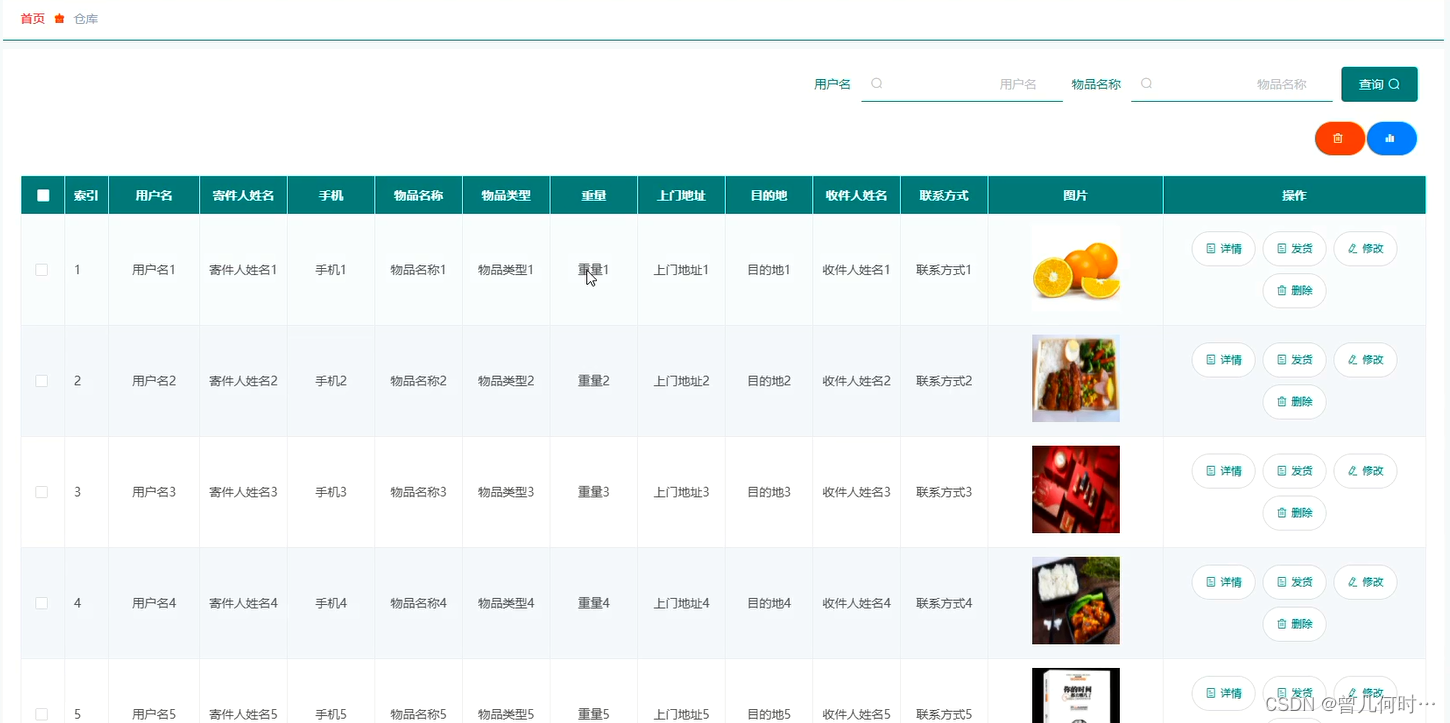
计算机毕业设计--基于SSM+Vue的物流管理系统的设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

GPT4 Plugins 插件 WebPilot 生成抖音文案
1. 生成抖音文案 1.1. 准备1篇优秀的抖音文案范例 1.2. Promept公式 你是一个有1000万粉丝的抖音主播, 请模仿下面的抖音脚本文案,重新改与一篇文章改写成2分钟的抖音视频脚本, 要求前一部分是十分有争议性的内容,并且能够引发…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

