实例9:四足机器人运动学正解平面RR单腿可视化
实例9:四足机器人正向运动学单腿可视化
实验目的
- 通过动手实践,搭建mini pupper四足机器人的腿部,掌握机器人单腿结构。
- 通过理论学习,熟悉几何法、旋转矩阵法在运动学正解(FK)中的用处。
- 通过编程实践,熟悉可视化简化机器人单腿的方法。
实验要求
通过Python编程,在简化的mini pupper平面二连杆模型内,让用户输入关节角,根据关节角及关节的基本信息,计算出每个关节相对于基坐标系的坐标,并将其可视化输出。
实验知识
1.什么是正向运动学 Forward Kinematics ?
在mini pupper的实际运动操作中,需要考虑计算小腿末端相对身体基座标系位置和姿态关系的静态几何问题。简单来说,就是给定一组关节角的值,计算小腿末端坐标系相对于基坐标系的位姿。
正向运动学探究的问题可以看做由关节空间Joint Space (θ1,θ2,⋅⋅⋅⋅,θn)(\theta_1,\theta_2,····,\theta_n)(θ1,θ2,⋅⋅⋅⋅,θn)描述到 笛卡尔空间Cartesian Space (WorldP)(^{World}P)(WorldP) 描述的位置表示。
探究这种位置的表示关系就是正向运动学,对于机器人来说,就是以操作臂的关节变量为自变量,描述操作臂末端执行器的位姿与基坐标系之间的函数关系。
2.怎么描述机器人的一条腿?
既然要考虑计算mini pupper实际运动中小腿末端相对身体基座标系位置和姿态关系的计算,就应该有对应的定性和定量的描述及表示来使得计算能够实现。
在机器人学中,操作臂由连杆link组成,将连杆视作刚体,相邻连杆由关节joint连接,关节可以相对 转动(revolute) 或者 移动(prismatic),转动的轴被称为Axis。
操作臂的这种描述对应到人体上,可以看作简化的人类的手臂,“大臂”就是一个连杆,通过“肘关节”这个关节和另一个连杆“小臂”相连,mini pupper也是相同的道理。
关节的转动和移动引出了两个数学量,对于转动关节,相邻杆件的相对角度变化被称为关节角,而对于移动关节,相邻杆件之间的相对位移变化被称为关节偏移量。
对于操作臂来说,自由度的数量是具有独立的位置变量的数目,常见的工业机器人大都是开式的运动链,每个关节位置由唯一变量来定义,因此关节的数目常常等于自由度的数量。
操作臂的末端被称为末端执行器,比如夹具、焊枪等,通常用设置在末端执行器上的工具坐标系Frame_Tool与操作臂的固定底座的参考基坐标系Frame_Base的相对关系,来描述操作臂的位置与姿态。
3.怎么描述腿间部件的关系?
为了描述相邻连杆之间的关系,引入了4个变量对连杆的空间关系进行描述。
| 名称 | 符号 | 含义 | 注释 |
|---|---|---|---|
| 连杆长度 | ai−1a_{i-1}ai−1 | 两个相邻关节轴之间公垂线的长度 | 连杆长度是沿着X^i−1\hat X_{i-1}X^i−1方向,Z^i−1\hat Z_{i-1}Z^i−1和Z^i\hat Z_{i}Z^i之间公垂线的长度。因为ai−1a_{i-1}ai−1是距离,所以始终有ai−1≥0a_{i-1}\geq0ai−1≥0。 |
| 连杆扭转角 | αi−1\alpha_{i-1}αi−1 | 沿着ai−1a_{i-1}ai−1方向的投影平面中两关节轴线的夹角 | 连杆扭转角是沿着X^i−1\hat X_{i-1}X^i−1方向看去所形成的的二维平面内Z^i−1\hat Z_{i-1}Z^i−1和Z^i\hat Z_{i}Z^i的夹角,按照右手法从Z^i−1\hat Z_{i-1}Z^i−1扭向Z^i\hat Z_{i}Z^i取正负。 |
| 连杆偏距 | did_{i}di | 沿两个相邻连杆公共轴线方向的距离。 | 沿着Z^i\hat Z_{i}Z^i方向看去,对于X^i−1\hat X_{i-1}X^i−1与Z^i\hat Z_{i}Z^i所在直线的相交点和X^i\hat X_{i}X^i与Z^i\hat Z_{i}Z^i所在直线的相交点,这两个相交点的距离。 |
| 关节角 | θi\theta_{i}θi | 两相邻连杆绕公共轴线旋转的角度。 | 沿着Z^i\hat Z_{i}Z^i方向看,二维平面内X^i−1\hat X_{i-1}X^i−1和X^i\hat X_{i}X^i的夹角,方向为X^i−1\hat X_{i-1}X^i−1扭向X^i\hat X_{i}X^i。 |
连杆扭转角和连杆长度定义了同一杆件的两个关节轴之间的关系,关节角和连杆偏距定义了连杆是如何连接的。
上表注释中提及的X^i\hat X_{i}X^i、Y^i\hat Y_{i}Y^i、Z^i\hat Z_{i}Z^i将在后文中结合连杆坐标系提及,可结合理解。
4.Denavit-Hartenberg表达法
简称为DH表达法,版本为Craig version,DH法是用四个连杆参数来描述机构运动关系的规则,两个参数用于描述连杆本身,另外两个参数用于描述连杆之间的连接关系。
这四个参数即是之前所提到的连杆扭转角αi−1\alpha_{i-1}αi−1、连杆长度ai−1a_{i-1}ai−1、关节角θi\theta_{i}θi、连杆偏距did_{i}di。
通常来说,对于转动关节,关节变量为关节角θi\theta_{i}θi,对于移动关节,关节变量为连杆偏距did_{i}di。
对于这类关节,除了关节变量外的其他的三个连杆参数都是固定不变的硬件属性参数。
5.连杆坐标系
为了描述连杆间的关系,坐标系被引入,因此需要在每个连杆上建立连杆坐标系,对于连杆i−1{i-1}i−1,其上有连杆坐标系{i−1}\{i-1\}{i−1},在Craig改良DH法中,连杆坐标系的原点通常被规定在在关节轴Axis(i−1)Axis_{(i-1)}Axis(i−1)上。
按照这种坐标系的规定,固定连杆坐标系的各正交轴如下:
| 轴或点 | 定义 |
|---|---|
| 原点 | 公垂线aia_iai与关节轴AxisiAxis_iAxisi的交点 |
| Z^i\hat Z_iZ^i | 与关节轴AxisiAxis_iAxisi重合 |
| X^i\hat X_iX^i | 沿着 公垂线aia_iai由关节jointijoint_ijointi指向关节jointi+1joint_{i+1}jointi+1方向。当公垂线ai=0a_i=0ai=0时,X^i\hat X_iX^i垂直于 Z^i\hat Z_iZ^i与 Z^i+1\hat Z_{i+1}Z^i+1形成的平面,可以有两个方向,根据方便选用 |
| Y^i\hat Y_iY^i | 根据右手定则确定,已知拇指为 X^i\hat X_iX^i,食指为Y^i\hat Y_iY^i ,已知中指为Z^i\hat Z_iZ^i |
连杆坐标系中的特殊存在
首端连杆
首端连杆被称为地杆,机器人的固定基座上的坐标系{0}\{0\}{0}常被用作参考坐标系。Z^0\hat Z_0Z^0方向和Z^1\hat Z_1Z^1相同,并当坐标系{1}\{1\}{1}的关节变量θi\theta_{i}θi或did_{i}di为0时,使坐标系{0}\{0\}{0}和坐标系{1}\{1\}{1}重合,以简化计算。
转动关节Revolute jointα0=0a0=0d1=0θ1=?(当为0时Frame重合)\text {转动关节Revolute joint} \quad \alpha_0=0 \quad a_0=0 \quad d_1=0 \quad\theta_1=?(当为0时Frame重合) 转动关节Revolute jointα0=0a0=0d1=0θ1=?(当为0时Frame重合)
移动关节Prismatic jointα0=0a0=0θ1=0d1=?(当为0时Frame重合)\text {移动关节Prismatic joint} \quad \alpha_0=0 \quad a_0=0 \quad \theta_1=0 \quad d_1=?(当为0时Frame重合) 移动关节Prismatic jointα0=0a0=0θ1=0d1=?(当为0时Frame重合)
末端连杆
末端杆没有下一根杆件,因此要和上一根杆件找关联。
对于转动关节,X^n\hat X_nX^n方向和X^n−1\hat X_{n-1}X^n−1相同,再选取设置原点使得dn=0d_n=0dn=0
对于移动关节,选取设置X^n\hat X_nX^n方向使得θn=0\theta_n=0θn=0,当dn=0d_n=0dn=0时,原点位于关节轴nnn和X^n−1\hat X_{n-1}X^n−1交点处
学习完连杆坐标系中,连杆参数可以更简单地理解:
| 名称 | 符号 | 含义 |
|---|---|---|
| 连杆扭转角 | αi−1\alpha_{i-1}αi−1 | 连杆扭转角是绕X^i−1\hat X_{i-1}X^i−1轴,Z^i−1\hat Z_{i-1}Z^i−1旋转到Z^i\hat Z_{i}Z^i的夹角 |
| 连杆长度 | ai−1a_{i-1}ai−1 | 连杆长度是沿着X^i−1\hat X_{i-1}X^i−1轴,Z^i−1\hat Z_{i-1}Z^i−1移动到Z^i\hat Z_{i}Z^i的公垂线的长度 |
| 关节角 | θi\theta_{i}θi | 绕Z^i\hat Z_{i}Z^i轴,X^i−1\hat X_{i-1}X^i−1旋转到X^i\hat X_{i}X^i的夹角 |
| 连杆偏距 | did_{i}di | 沿着Z^i\hat Z_{i}Z^i轴,X^i−1\hat X_{i-1}X^i−1移动到X^i\hat X_{i}X^i的距离 |
建立连杆坐标系和DH表
- 找出关节轴
分析运动状态,找出关节平移或转动的轴向(joint axes) - 找出Z^i\hat Z_{i}Z^i
Z^i\hat Z_{i}Z^i的正方向为转动或移动的轴axis方向 - 找出X^i\hat X_{i}X^i
X^i\hat X_{i}X^i的正方向是两个关节轴之间公垂线上,指向下一个关节轴的方向
(ai=0a_i=0ai=0时,即当两关节轴相交时,XXX和ZiZ_iZi和Zi+1Z_{i+1}Zi+1的方向垂直,此时方向怎么方便怎么来) - 确定原点
原点即为Z^i\hat Z_{i}Z^i与X^i\hat X_{i}X^i的交点 - 找出Y^i\hat Y_{i}Y^i
根据右手定则确定,拇指为 X^i\hat X_iX^i,食指为Y^i\hat Y_iY^i ,中指为Z^i\hat Z_iZ^i - 处理首端连杆
并当Frame1Frame_1Frame1的关节变量θi\theta_{i}θi或did_{i}di为0时,使Frame0Frame_0Frame0和Frame1Frame_1Frame1重合,以简化计算。 - 处理末端连杆
尽量使得连杆参数为0以简化计算
根据以上几步处理的结果,可以获取DH参数表
DH参数表是Frame之间的关系,每个i代表一对轴之间的关系
表中的1为基坐标系Frame0Frame_0Frame0与第一个轴坐标系Frame1Frame_1Frame1的关系
表中的3为末端连杆与最后一个可(转、平移)的轴的关系
| i | αi−1\alpha_{i-1}αi−1 | ai−1a_{i-1}ai−1 | θi\theta_iθi | did_idi |
|---|---|---|---|---|
| 1 | 0 | 0 | θ1\theta_1θ1 | 0 |
| 2 | 0 | L1L_1L1 | θ2\theta_2θ2 | 0 |
| 3 | 0 | L2L_2L2 | θ3\theta_3θ3 | 0 |
6.连杆坐标系之间的转化
对于Framei−1Frame_{i-1}Framei−1,要从Axisi−1Axis_{i-1}Axisi−1到AxisiAxis_{i}Axisi。
首先,完成从Z^i−1\hat Z_{i-1}Z^i−1到Z^i\hat Z_{i}Z^i的旋转αi−1\alpha_{i-1}αi−1和平移ai−1a_{i-1}ai−1距离。
然后,将旋转和平移后的Axisi−1Axis_{i-1}Axisi−1旋转θi\theta_{i}θi,并沿着Z^i\hat Z_{i}Z^i方向平移did_{i}di距离。
总计进行四次操作,最终可得
i−1P=ii−1TiP^{i-1}P=^{i-1}_iT^{i}P i−1P=ii−1TiP
ii−1T^{i-1}_iTii−1T中合并了这四次操作,得出该变换矩阵:
ii−1T=[Cosθi−Sinθi0ai−1SinθiCosαi−1CosθiCosαi−1−Sinαi−1−Sinαi−1diSinθiSinαi−1CosθiSinαi−1Cosαi−1Cosαi−1di0001]^{i-1}_iT= \left[ \begin{matrix} Cos\theta_i & -Sin\theta_i & 0 & a_{i-1} \\ Sin\theta_iCos\alpha_{i-1} & Cos\theta_iCos\alpha_{i-1} & -Sin\alpha_{i-1} &-Sin\alpha_{i-1}d_i\\ Sin\theta_iSin\alpha_{i-1} & Cos\theta_iSin\alpha_{i-1} & Cos\alpha_{i-1} &Cos\alpha_{i-1}d_i\ \\ 0&0&0&1 \end{matrix} \right] ii−1T=CosθiSinθiCosαi−1SinθiSinαi−10−SinθiCosθiCosαi−1CosθiSinαi−100−Sinαi−1Cosαi−10ai−1−Sinαi−1diCosαi−1di 1
多次使用该变换矩阵可以得出不相邻的关节之间的转化关系
7.mini pupper的简化运动学结构
mini pupper的单条腿部可简化视作典型的三连杆非平面操作臂,三自由度的设计使得它理论上能够到达空间限位范围内的任意位置。
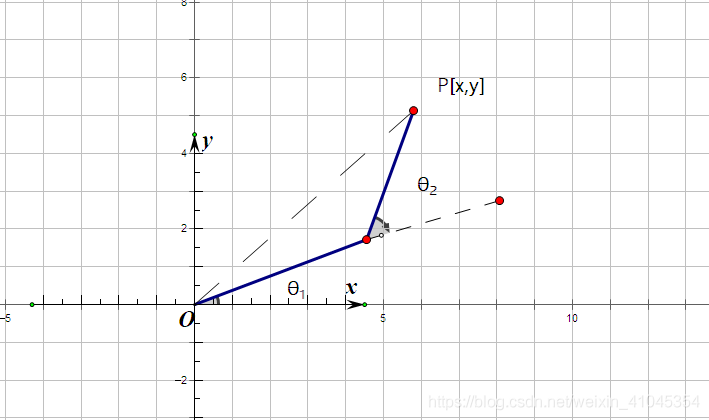
当我们进一步简化,不考虑横向髋关节运动时,mini pupper的腿部可以简化为平面二连杆机构RR模型,使用几何解法即可在已知θ1\theta_1θ1和θ2\theta_2θ2的情况下求得0P^0P0P的坐标,完成运动学正解。
对于大臂与小臂相交处QQQ:
xq=l1Cosθ1x_q=l_1Cos\theta_1 xq=l1Cosθ1
yq=l1Sinθ1y_q=l_1Sin\theta_1 yq=l1Sinθ1
对于小臂末端点:
xp=l1Cosθ1+l2Cos(θ1+θ2)x_p=l_1Cos\theta_1+l_2Cos(\theta_1+\theta_2) xp=l1Cosθ1+l2Cos(θ1+θ2)
yp=l1Sinθ1+l2Sin(θ1+θ2)y_p=l_1Sin\theta_1+l_2Sin(\theta_1+\theta_2) yp=l1Sinθ1+l2Sin(θ1+θ2)
图片:平面二连杆机构RR模型
实验步骤
1. 编写Python代码 rr_manipulator.py
#!/usr/bin/python
# coding:utf-8
# rr_manipulator.py
# mini pupper的简化单腿,可视作同一平面的RR类机械臂,可视化该机械臂,由给定角度计算末端点位置
import matplotlib.pyplot as plt # 引入matplotlib
import numpy as np # 引入numpy
from math import radians, sin, cos# 几何法:关节角转端点坐标
def theta_2_position_rr(l1, l2, theta1, theta2):"""运动学正解 将输入的关节角转化为对应的端点坐标:param l1: 大臂长:param l2: 小臂长:param theta1: 大臂关节角:param theta2: 小臂关节角:return: 端点1坐标 端点2坐标"""point_1 = [l1*cos(radians(theta1)), l1*sin(radians(theta1))]point_2 = [l1*cos(radians(theta1))+l2*cos(radians(theta1+theta2)),l1*sin(radians(theta1))+l2*sin(radians(theta1+theta2))]print(point_1)print(point_2)return point_1, point_2def preprocess_drawing_data(points):"""处理点坐标数据转化为matplotlib适应的绘图格式:param points: 点数据:return: 绘图数据x坐标list和对应的y坐标list"""xs = [0]ys = [0]xs.append(points[0][0])xs.append(points[1][0])ys.append(points[0][1])ys.append(points[1][1])return xs, ys# 关节信息
# 大臂长度:5 cm 小臂长度:6 cm
link_length = [5, 6] # in cm# 关节角初始化
joints_angle_origin = [30, 30]
joints_angle = [0, 0]
print("关节角初始状态 theta1=%d°, theta2=%d°" % (joints_angle_origin[0], joints_angle_origin[1]))# 输入连杆参数:各关节角
for i in range(1, 3):joints_angle[i-1] = int(input("请输入腿部舵机[%d]要转动的的角度:" % i))print("腿部舵机[{0}]将转动{1}°".format(i, joints_angle[i-1]))# 计算并预处理绘图数据
points_origin = theta_2_position_rr(link_length[0], link_length[1], joints_angle_origin[0], joints_angle_origin[1])
points_after = theta_2_position_rr(link_length[0], link_length[1], joints_angle[0], joints_angle[1])
data_origin = preprocess_drawing_data(points_origin)
data_after = preprocess_drawing_data(points_after)# 绘图
fig, ax = plt.subplots() # 建立图像
plt.plot(data_origin[0], data_origin[1], color='black', label='original')
plt.scatter(data_origin[0], data_origin[1], color='black')
plt.plot(data_after[0], data_after[1], color='red', label='after')
plt.scatter(data_after[0], data_after[1], color='blue')
ax.set(xlabel='X', ylabel='Y', title='mini pupper FK RR model')
ax.grid()
plt.legend()
plt.show()
2. 运行程序,观察效果
在rr_manipulator.py的目录下执行以下命令:
sudo python rr_manipulator.py
此时应观察到根据关节角计算出的可视化坐标。
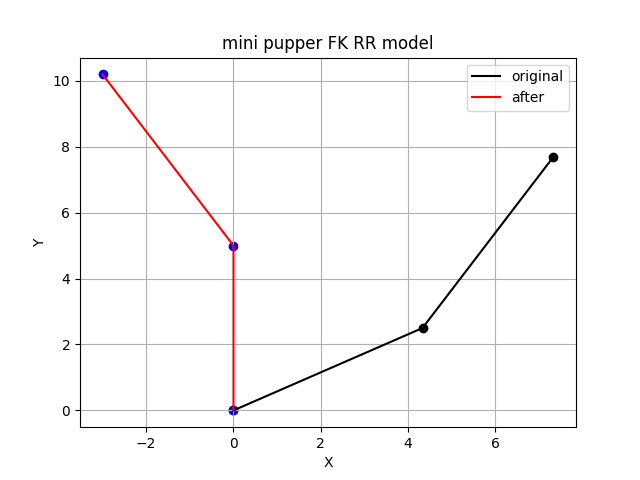
实验总结
经过本知识点的学习和实验操作,你应该能达到以下水平:
| 知识点 | 内容 | 了解 | 熟悉 | 掌握 |
|---|---|---|---|---|
| 硬件 | mini pupper单腿结构的搭建 | ✔ | ||
| 运动学 | 平面RR类型机械臂的运动学正解 | ✔ | ||
| 运动学 | 非平面RRR类型机械臂 | ✔ | ||
| 运动学 | 几何法完成运动学正解 | ✔ | ||
| 运动学 | 运动学正解基础知识 | ✔ | ||
| 可视化 | Python可视化运动学 | ✔ |
版权信息:教材尚未完善,此处预留版权信息处理方式
mini pupper相关内容可访问:https://github.com/mangdangroboticsclub
相关文章:

实例9:四足机器人运动学正解平面RR单腿可视化
实例9:四足机器人正向运动学单腿可视化 实验目的 通过动手实践,搭建mini pupper四足机器人的腿部,掌握机器人单腿结构。通过理论学习,熟悉几何法、旋转矩阵法在运动学正解(FK)中的用处。通过编程实践&…...
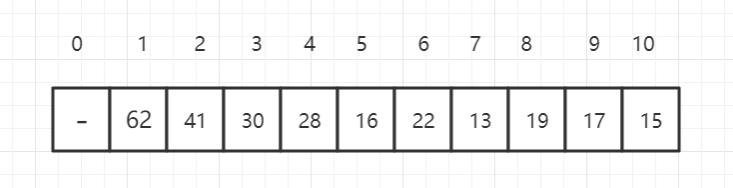
堆的基本存储
一、概念及其介绍堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。堆满足下列性质:堆中某个节点的值总是不大于或不小于其父节点的值。堆总是一棵完全二叉树。二、适用说明堆是利用完全二叉树的结构来维护一组数…...

如何获取物体立体信息通过一个相机
大家都知道的3D 技术是通过双眼视觉差异 得到的 但是3D的深度并没有那么强 为什么眼睛看到的就那么强 这无法让我们相信这个视觉差理论是和人眼睛立体感是一个原理 这个如今3D 电影都在用的技术 是和真正的人眼立体感 不一样的 或者说是有瑕疵的 分析一下现在的立体感技术 是通…...
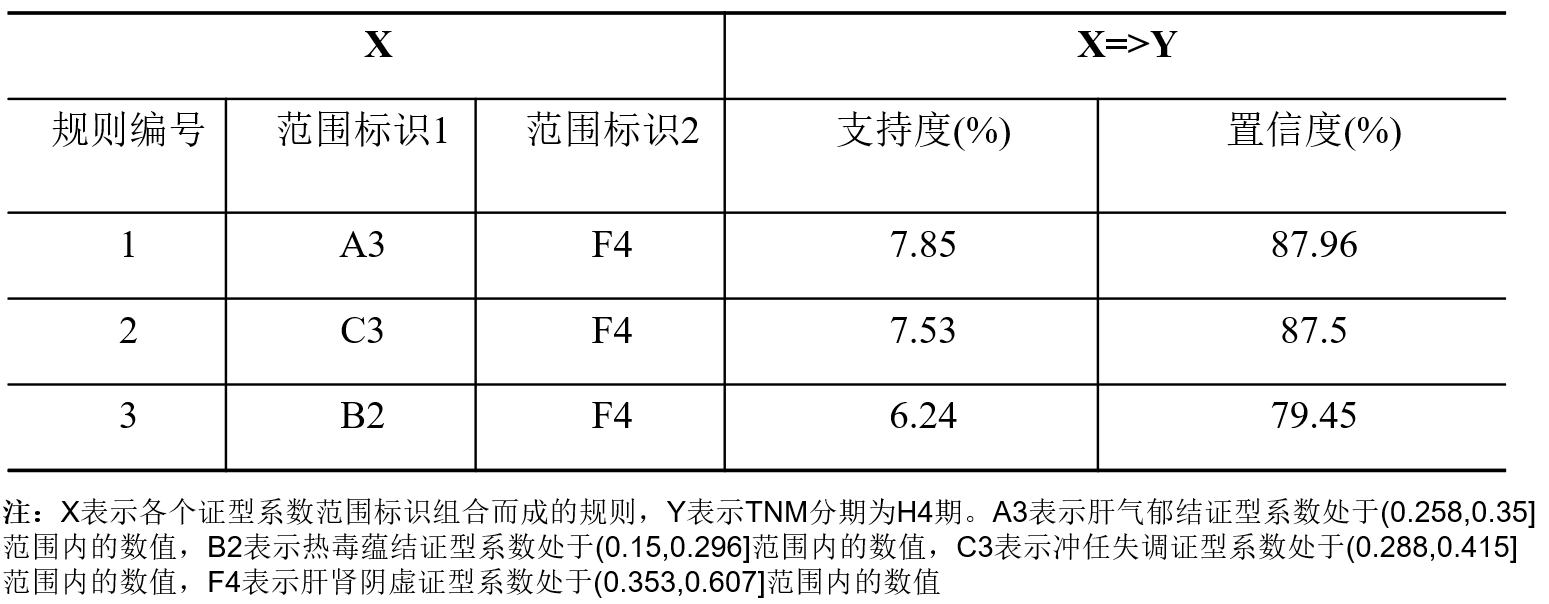
【数据挖掘实战】——中医证型的关联规则挖掘(Apriori算法)
目录 一、背景和挖掘目标 1、问题背景 2、传统方法的缺陷 3、原始数据情况 4、挖掘目标 二、分析方法和过程 1、初步分析 2、总体过程 第1步:数据获取 第2步:数据预处理 第3步:构建模型 三、思考和总结 项目地址:Data…...
一些硬件学习的注意事项与快捷方法
xilinx系列软件 系统适用版本 要安装在Ubuntu系统的话,要注意提前看好软件适用的版本,不要随便安好了Ubuntu系统又发现对应版本的xilinx软件不支持。 如下图,发行说明中会说明这个版本的软件所适配的系统版本。 下载 vivado vitis这些都可以…...
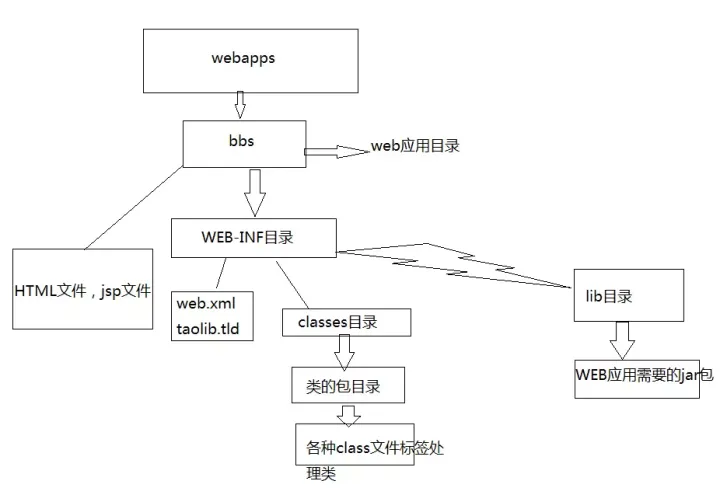
【Tomcat】Tomcat安装及环境配置
文章目录什么是Tomcat为什么我们需要用到Tomcattomcat下载及安装1、进入官网www.apache.org,找到Projects中的project List2、下载之后,解压3、找到tomcat目录下的startup.bat文件,双击之后最后结果出现多少多少秒,表示安装成功4、…...
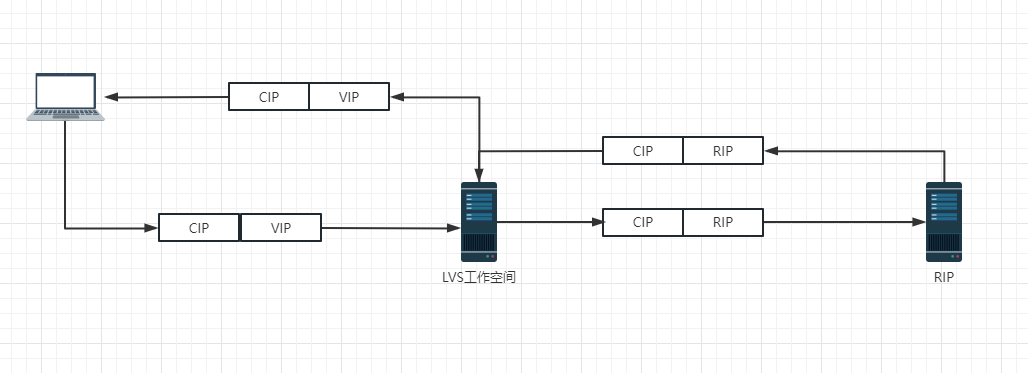
负载均衡:LVS 笔记(二)
文章目录LVS 二层负载均衡机制LVS 三层负载均衡机制LVS 四层负载均衡机制LVS 调度算法轮叫调度(RR)加权轮叫调度(WRR)最小连接调度(LC)加权最小连接调度(WLC)基于局部性的最少链接调…...
SEO优化:干货技巧分享,包新站1-15天100%收录首页
不管是老域名还是新域名,不管是多久没有收录首页的站,此法周期7-30天,包首页收录!本人不喜欢空吹牛逼不实践的理论,公布具体操作:假如你想收录的域名是a.com,那么准备如下材料1.购买5-10个最便宜…...

JavaWeb测试题
【第四小组】【姓名:郑梦飞】说明:上方【组】填入所在的组,上方【姓名】填入自己的真实姓名。答题方式,基于Word文档基础上答题编程题可利用工具编程完以后,复制到该文档内。答完以后,导成PDF。以姓名.PDF命…...
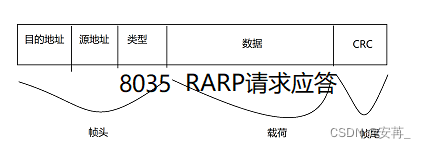
Java EE|TCP/IP协议栈之数据链路层协议详解
文章目录一、数据链路层协议感性认识数据链路层简介以太网简介特点二、以太网数据帧格式详解帧头不同类型对应的载荷三、关于MTU什么是MTUMTU有什么作用ip分片(了解)参考一、数据链路层协议感性认识 数据链路层简介 从上图可以看出 , 在TCP/…...
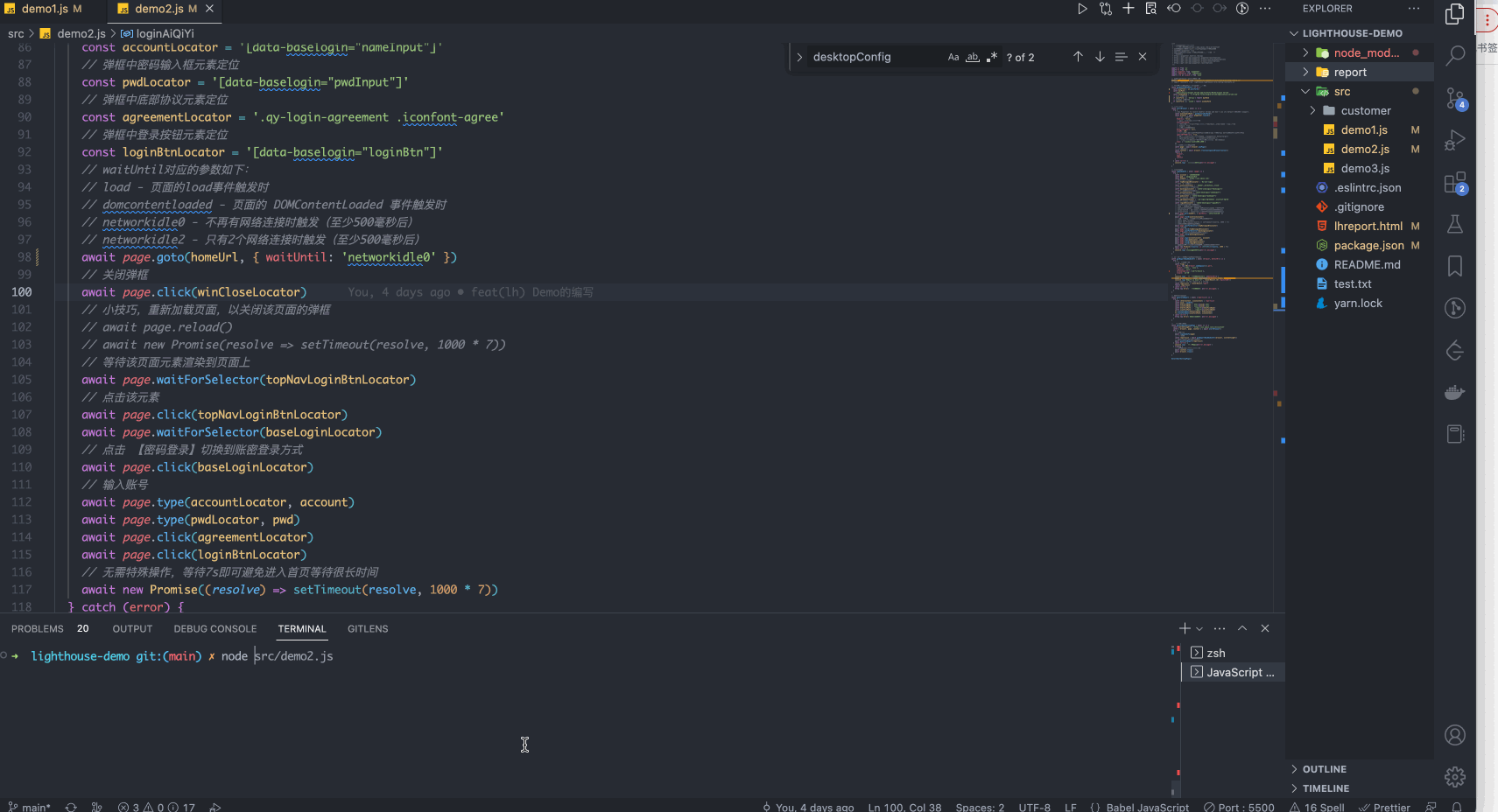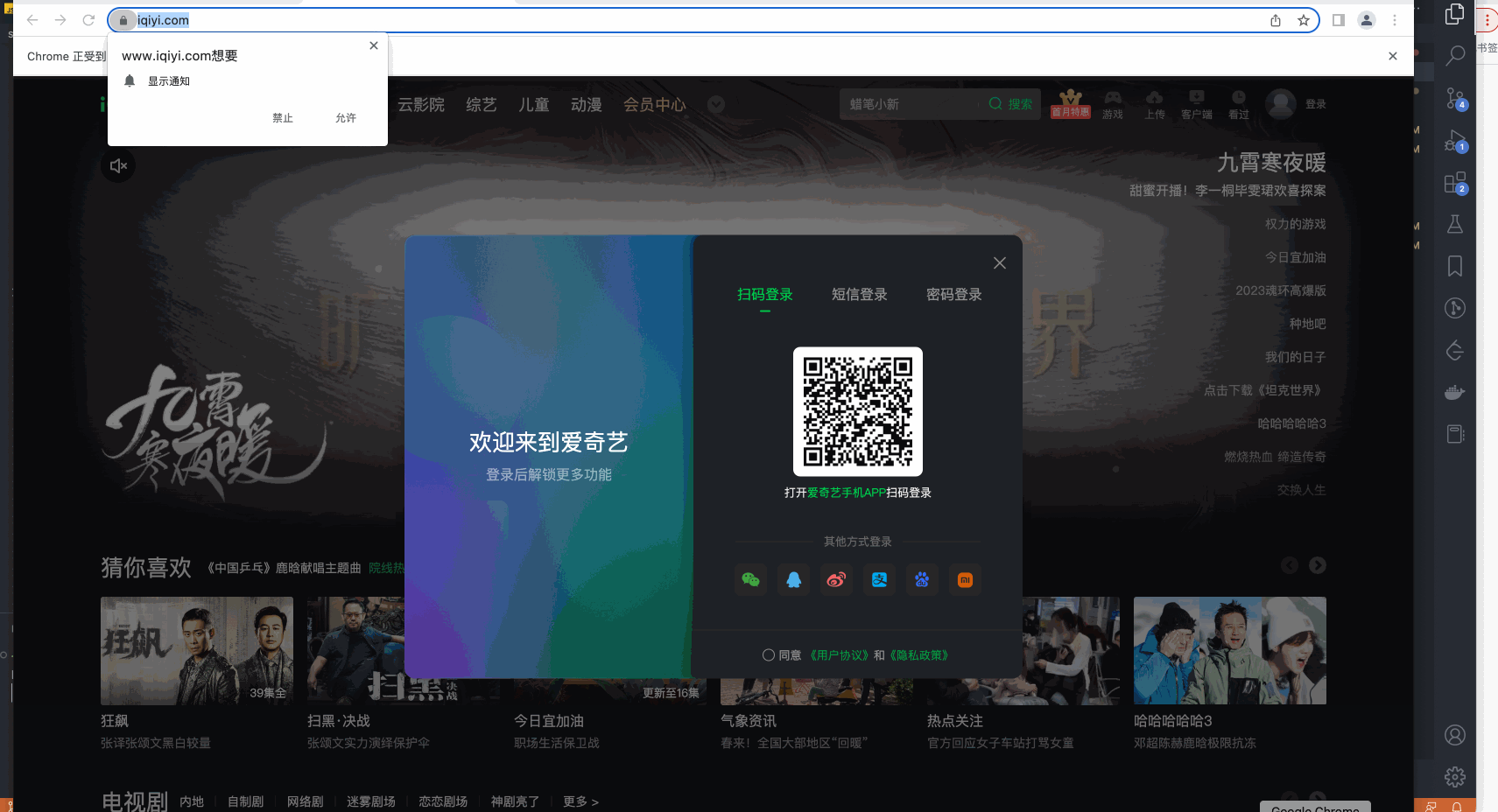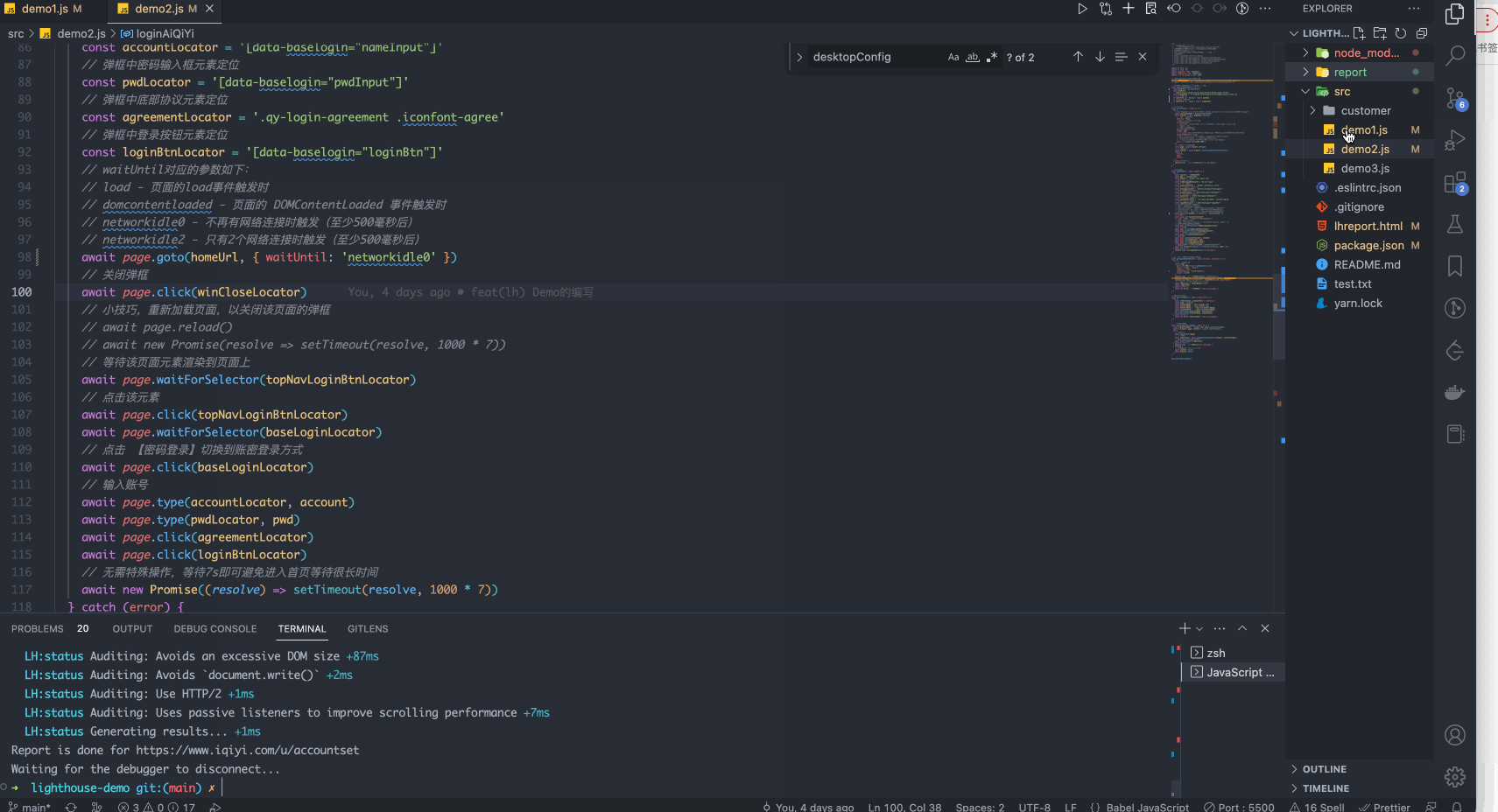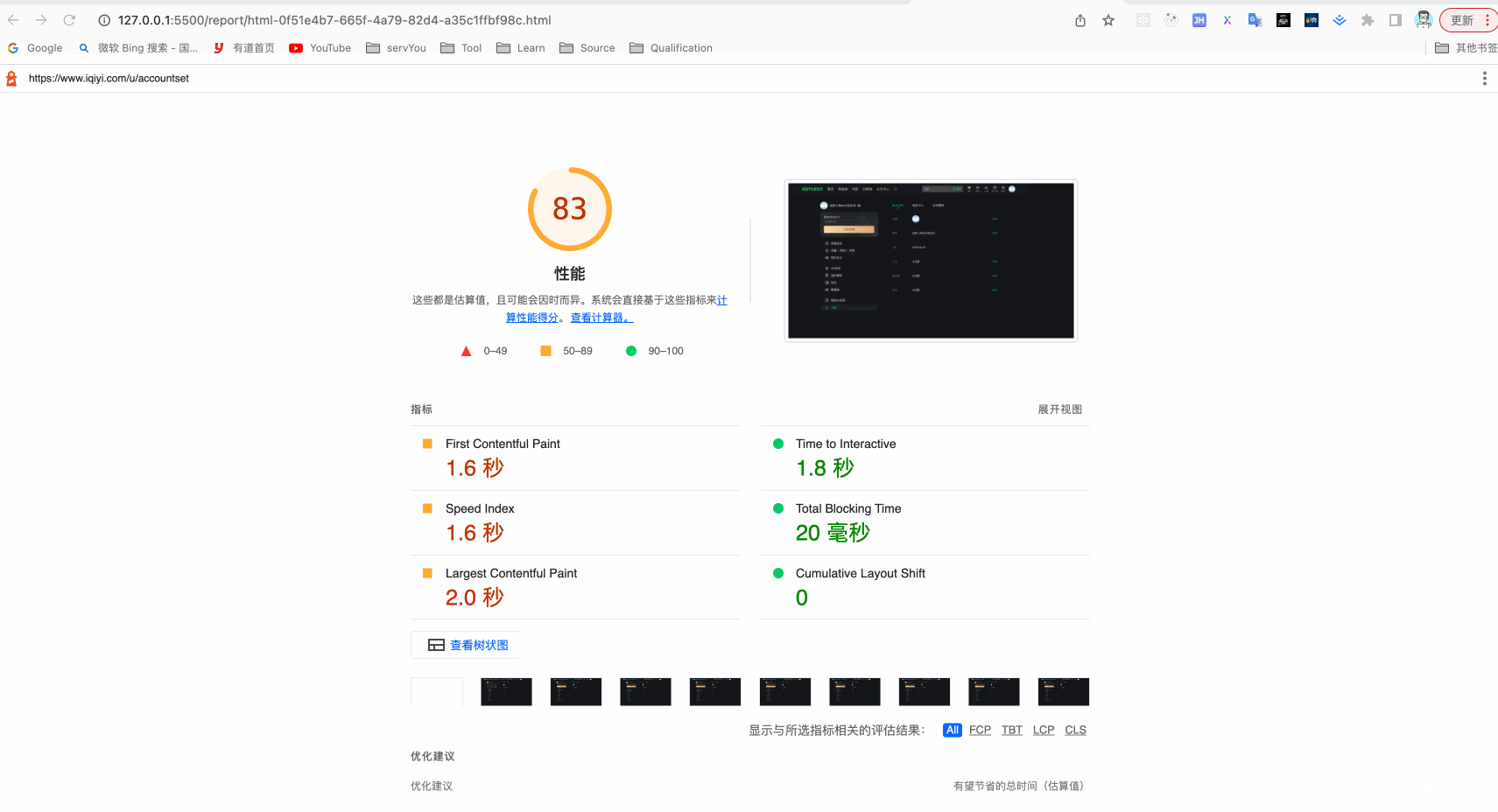
Lighthouse组合Puppeteer检测页面
如上一篇文章lighthouse的介绍和基本使用方法结尾提到的一样,我们在实际使用Lighthouse检测页面性能时,通常需要一定的业务前置条件,比如最常见的登录操作、如果没有登录态就没有办法访问其他页面。再比如有一些页面是需要进行一系列的操作&a…...
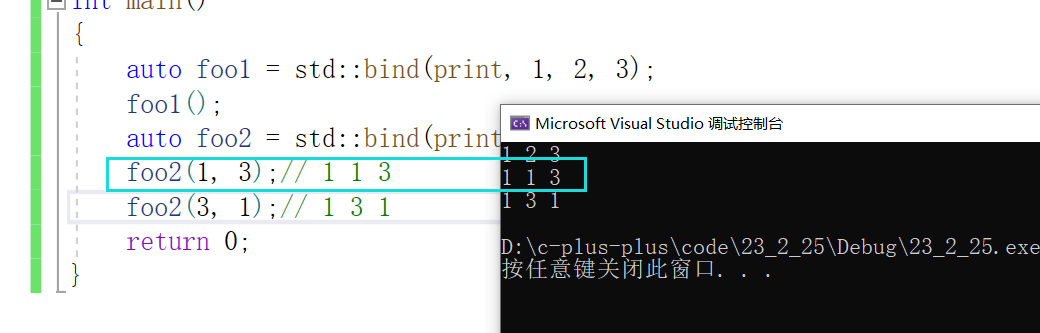
【C++】仿函数、lambda表达式、包装器
1.仿函数 仿函数是什么?仿函数就是类中的成员函数,这个成员函数可以让对象模仿函数调用的行为。 函数调用的行为:函数名(函数参数)C中可以让类实现:函数名(函数参数)调用函数 自己写一个仿函数: 重载()运算符 cla…...
)
二叉树(二)
二叉树——堆存储1.堆的初始化2. 堆的销毁3.堆的插入4.堆的删除5.堆的打印6.取堆顶的数据7.堆的数据个数8.堆的判空9.堆的构建10.向上调整11.向下调整12.使用堆进行排序13.交换14.完整代码🌟🌟hello,各位读者大大们你们好呀🌟&…...

爬虫知识简介
爬虫简介 爬虫与网络请求 网络爬虫是一个自动提取网页的程序,一般都分为3步:数据爬取,数据解析,数据存储。数据爬取就是模拟浏览器发送请求,所以需要对网络请求HTTP/HTTPS有一定了解 相关概念: H…...

2023年全国最新会计专业技术资格精选真题及答案6
百分百题库提供会计专业技术资格考试试题、会计考试预测题、会计专业技术资格考试真题、会计证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 11.下列各项中,企业根据本月“工资费用分配汇总表”分配所列财务部门…...

同时学习C++语言和C#语言好吗?
同时学习两门编程语言并不是不好的选择,尤其是对于初学者而言,这样做能够帮助你更好地理解编程语言的基本概念和原则。C和C#都是常用的编程语言,它们都有各自的优点和用途。同时学习这两门语言能够让你更好地理解它们之间的异同点,…...

Android8,source与lunch流程解析
source 流程 # build/make/envsetup.sh ---- # Execute the contents of any vendorsetup.sh files we can find. for f in test -d device && find -L device -maxdepth 4 -name vendorsetup.sh 2> /dev/null | sort \ test -d vendor && find -L vendo…...
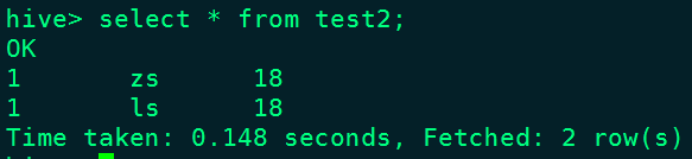
大数据NiFi(二十):实时同步MySQL数据到Hive
文章目录 实时同步MySQL数据到Hive 一、开启MySQL的binlog日志 1、登录mysql查看MySQL是否开启binlog日志 2 、开启mysql binlog日志 3、重启mysql 服务,重新查看binlog日志情况 二、配置“CaptureChangeMySQL”处理器 1、创建“…...
mac 如何设置 oh my zsh 终端terminal 和添加主题powerlevel10k
Oh My Zsh 是什么 Oh My Zsh 是一款社区驱动的命令行工具,正如它的主页上说的,Oh My Zsh 是一种生活方式。它基于 zsh 命令行,提供了主题配置,插件机制,已经内置的便捷操作。给我们一种全新的方式使用命令行。 **Oh …...
王道《操作系统》学习(一)——计算机系统概述
1.1 操作系统的概念、功能 1.1.1 操作系统的概念(定义) (1)操作系统是系统资源的管理者 (2)向上层用户、软件提供方便易用的服务 (3)是最接近硬件的一层软件 1.1.2 操作系统的功能…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
