基于秃鹰算法的无人机航迹规划-附代码
基于秃鹰算法的无人机航迹规划
文章目录
- 基于秃鹰算法的无人机航迹规划
- 1.秃鹰搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用秃鹰算法来优化无人机航迹规划。
1.秃鹰搜索算法
秃鹰算法原理请参考:https://blog.csdn.net/u011835903/article/details/113775430
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得秃鹰搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用秃鹰算法对航迹评价函数式(7)进行优化。优化结果如下:


从结果来看,秃鹰算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于秃鹰算法的无人机航迹规划-附代码
基于秃鹰算法的无人机航迹规划 文章目录 基于秃鹰算法的无人机航迹规划1.秃鹰搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用秃鹰算法来优化无人机航迹规划。 1.秃鹰搜索算法 …...
08. 按键输入
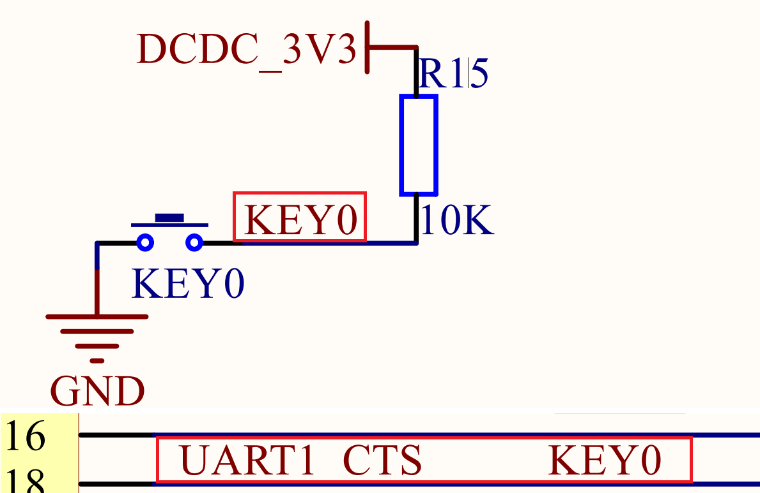
08. 按键输入 按键原理图代码编写GPIO驱动代码按键驱动代码主函数 加上清除BSS段,代码不运行 按键原理图 按键KEY0连接到了UART1_CTS上。默认情况下,KEY0为高,当按下KEY0后,UART1_CTS为低电平 代码编写 在bsp下创建一个key和一个…...

YOLOv8-pose关键点检测:模型轻量化创新 |轻量高性能网络PPLCNet助力backbone
💡💡💡本文解决什么问题:轻量高性能网络PPLCNet替换YOLOv8 backbone PPLCNet | GFLOPs从9.6降低至6.6, mAP50从0.921下降至0.901,mAP50-95从0.697提升至0.752 Yolov8-Pose关键点检测专栏介绍:https://blog.csdn.net/m0_63774211/category_12398833.html ✨✨✨手…...

大数据笔记-关于Cassandra的删除问题
Cassandra是Facebook开源的一个NoSQL数据库,它除了具备一般的NoSQL分布式数据库特点以外,最大的一个特点是去中心化架构设计,这和Hadoop HDFS/HBase等不一样,比如HDFS分为NameNode和DataNode,而Cassandra集群中所有节点…...

Qt自定义文件选择框
文章目录 前言一、头文件二、源文件三、qss文件四、效果 前言 在开发过程中,经常遇到使用文件选择框的情况,qt默认的文件选择框,样式可能与开发的桌面程序差异比较大.此时,我们可以自定义文件选择框,设置其样式,尽量做到样式统一. 一、头文件 #ifndef CUSTOMFILEDIALOG_H #d…...
金蝶云星空创建自动下推并保存公共服务
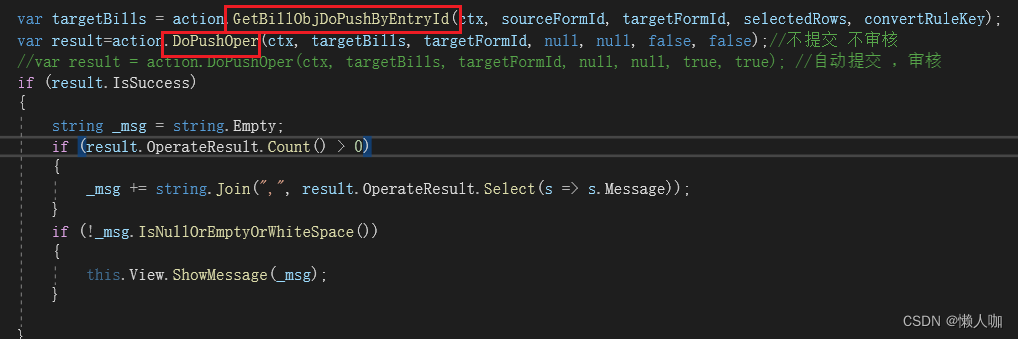
文章目录 金蝶云星空创建自动下推并保存公共服务创建公共方法按单下推数据按明细行下推数据调用下推操作 调用公共方法 金蝶云星空创建自动下推并保存公共服务 创建公共方法 按单下推数据 /// <summary>/// 获取单据转换数据包/// </summary>public DynamicObjec…...

人大金仓助力中国人民银行征信中心业务系统异地容灾优化升级
日前,人大金仓助力中国人民银行应收账款融资服务平台异地容灾项目顺利上线,保证了平台系统运行的连续性和数据安全,为充分发挥平台的融资功能,缓解中小微企业融资难提供了强有力的保障。 缓解中小微企业融资难 中国人民银行构于2…...

[架构之路-249/创业之路-80]:目标系统 - 纵向分层 - 企业信息化的呈现形态:常见企业信息化软件系统 - 产品(数据)管理
目录 前言: 一、企业信息化的结果:常见企业信息化软件 1.1 产品数据管理 1.1.1 什么是产品数据管理What 1.1.1.1 常见工具 1.1.1.2 软件企业的产品数据管理系统 1.1.2 为什么需要产品数据管理系统Why? 1.1.3 谁需要产品数据管理系统w…...

【NI-DAQmx入门】传感器基础知识
1.什么是传感器? 传感器可将真实的现象(例如温度或压力)转换为可测量的电流和电压,因而对于数据采集应用必不可少。接下来我们将介绍您所需的测量类型及其对应的传感器类型。在开始之前,您还可以先了解一些传感器术语&…...
CMake:构建时为特定目标运行自定义命令
CMake:构建时为特定目标运行自定义命令 导言项目结构相关源码结果 导言 add_custom_command 是 CMake 中用于添加自定义构建规则的命令,通常用于在编译项目时执行一些自定义操作,例如生成文件、运行脚本等。 项目结构 . ├── CMakeLists…...

基于适应度相关算法的无人机航迹规划-附代码
基于适应度相关算法的无人机航迹规划 文章目录 基于适应度相关算法的无人机航迹规划1.适应度相关搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用适应度相关算法来优化无人机航迹…...
jmeter BeanShell预处理程序:报错Error invoking bsh method: eval...
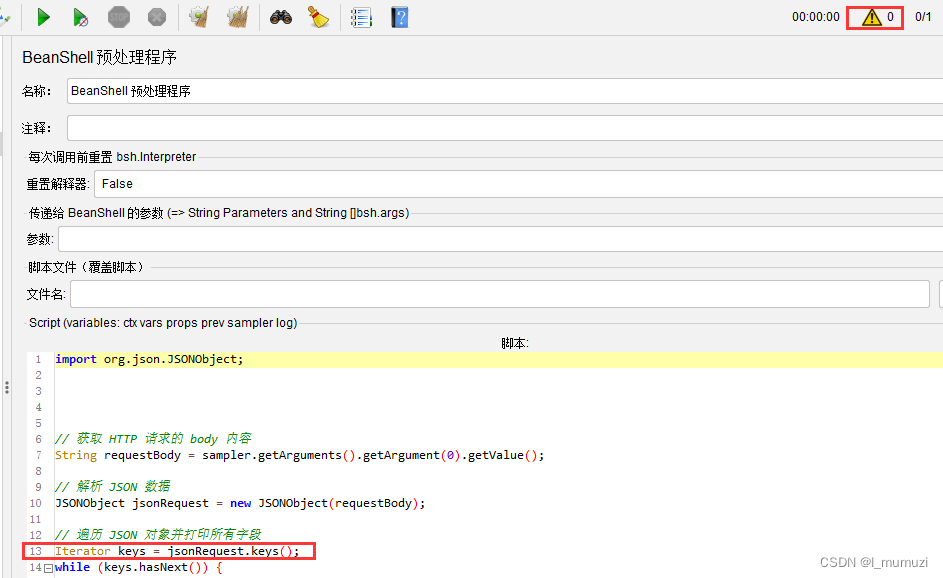
1、jmeter运行报错: ERROR o.a.j.u.BeanShellInterpreter: Error invoking bsh method: eval In file: inline evaluation of: " . . . Encountered "" at line 13, column 23. WARN o.a.j.m.BeanShellPreProcessor: Problem in BeanShell scri…...

使用springboot对Elasticsearch 进行索引的增、删、改、查
一 SpringBoot Elasticsearch 项目环境搭建 1.1 修改pom文件添加依赖 目前使用spring-boot-starter-parent版本为2.2.8.RELEASE 对应spring-data-elasticsearch版本为2.2.8.RELEASE,版本对应可以自行百度,如果不行直接用elasticsearch-rest-high-lev…...

Project#2: Extendible Hash Index
文章目录 准备Task #1-Read/Write Page GuardsBasicPageGuard/ReadPageGuard/WritePageGuardUpgradeWrappersTests Task #2-Extendible Hash Table PagesHash Table Header Pages**成员变量:****方法实现:** Hash Table Directory Pages**成员变量&#…...
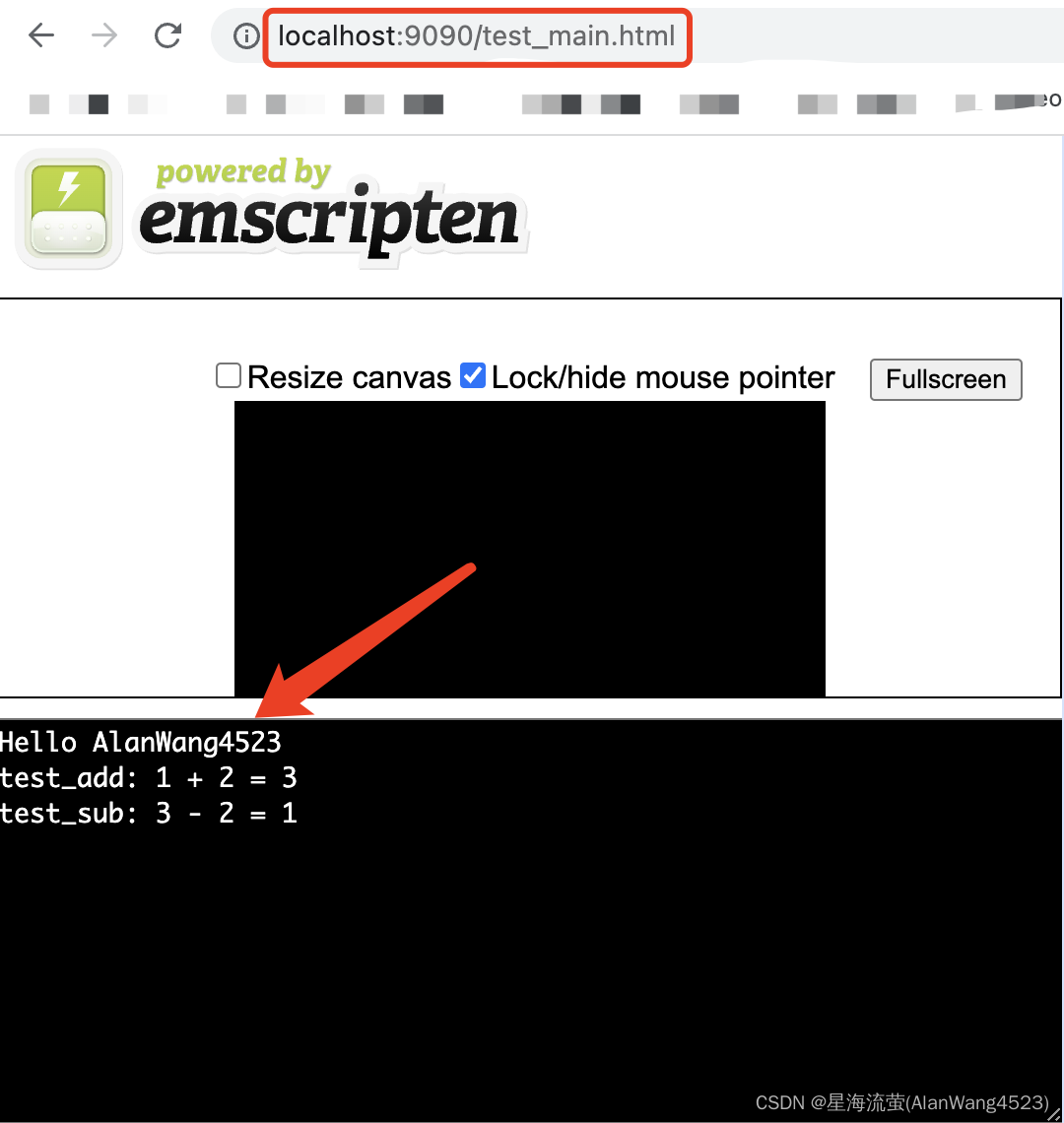
Emscripten + CMakeLists.txt 将 C++ 项目编译成 WebAssembly(.wasm)/js,并编译 Html 测试
背景:Web 端需要使用已有的 C 库(使用 CMake 编译),需要将 C 项目编译成 WebAssembly(.wasm) 供 js 调用。 上篇文章《Mac 上安装 Emscripten》 已讲解如何安装配置 Emscripten 环境。 本篇文章主要讲解如何将基于 CMakeLists 配…...
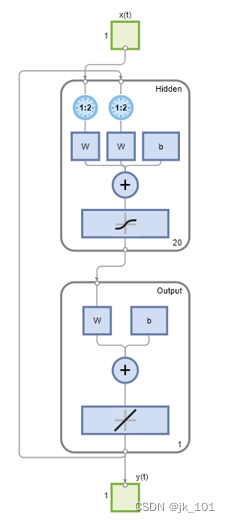
MATLAB中preparets函数用法
目录 语法 说明 示例 准备开环和闭环网络的数据 preparets函数的功能是为网络模拟或训练准备输入和目标时间序列数据 语法 [Xs,Xi,Ai,Ts,EWs,shift] preparets(net,Xnf,Tnf,Tf,EW) 说明 [Xs, Xi, Ai, Ts, EWs, shift] preparets(net, Xnf, Tnf, Tf, EW) 这个函数接受…...
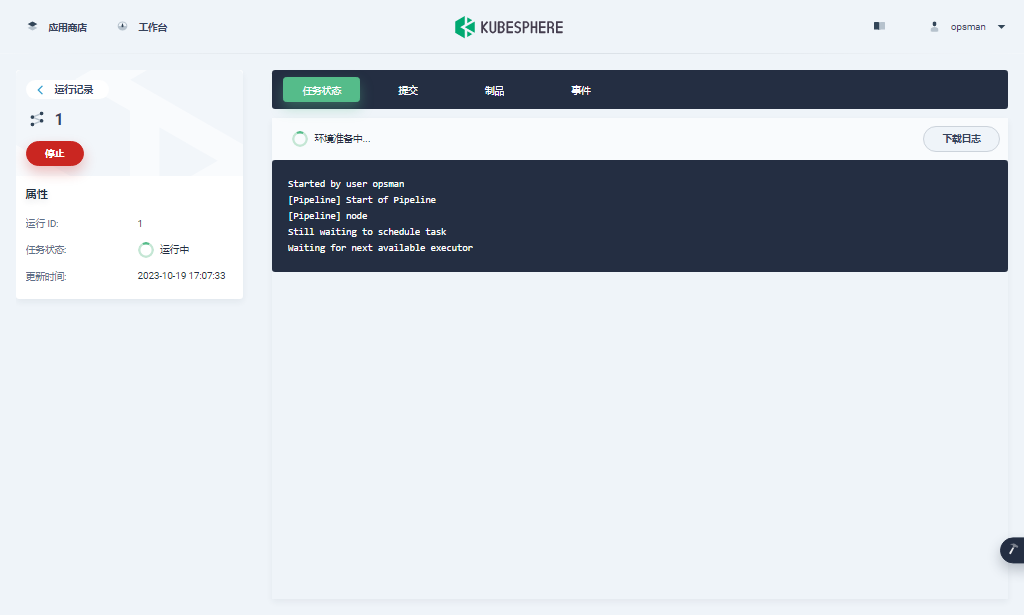
ARM 版 OpenEuler 22.03 部署 KubeSphere v3.4.0 不完全指南续篇
作者:运维有术 前言 知识点 定级:入门级KubeKey 安装部署 ARM 版 KubeSphere 和 KubernetesARM 版 KubeSphere 和 Kubernetes 常见问题 实战服务器配置 (个人云上测试服务器) 主机名IPCPU内存系统盘数据盘用途ks-master-1172.16.33.1661650200KubeSp…...

react官网
应急方案 – React 中文文档 (docschina.org) 正版卡死版 Hooks FAQ – React (reactjs.org) 英文流畅版 应急方案 – React 中文网 (nodejs.cn) 盗版流畅版(翻译有稍稍的问题) http://www.react-cn.com/index.html 黄版...
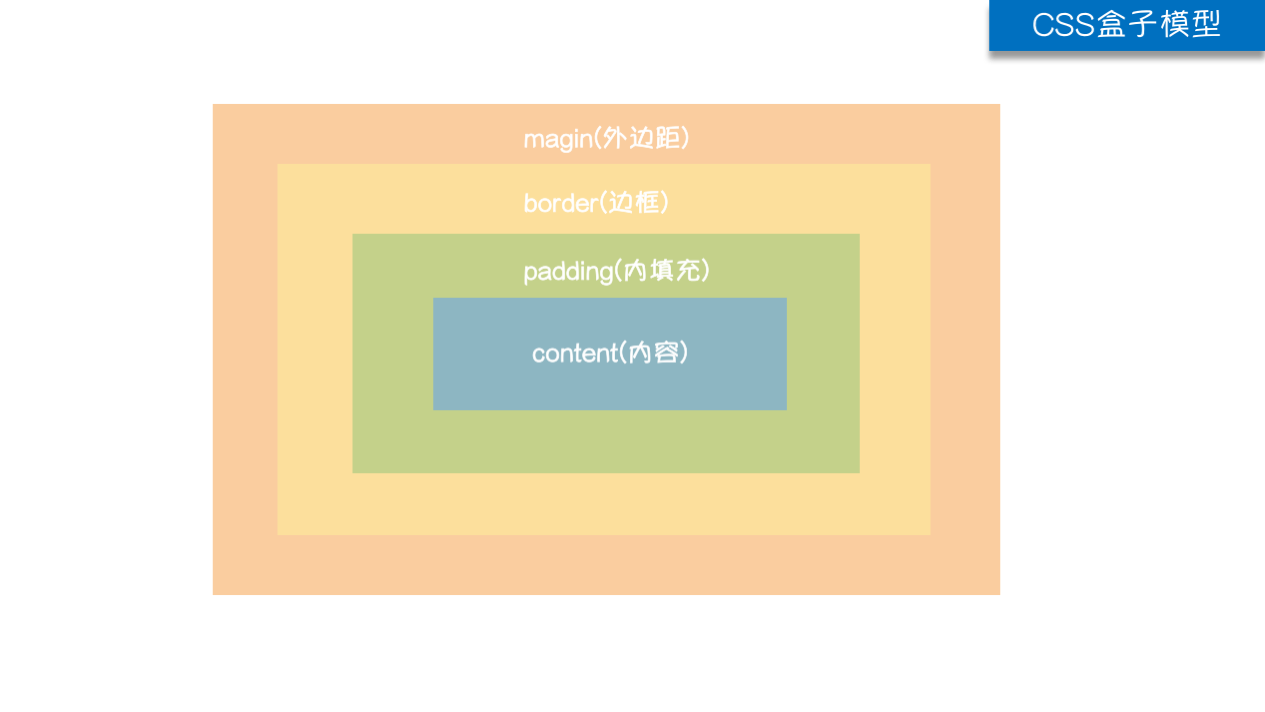
前端css介绍
CSS介绍 CSS(Cascading Style Sheet,层叠样式表)定义如何显示HTML元素。 当浏览器读到一个样式表,它就会按照这个样式表来对文档进行格式化(渲染)。 CSS语法 CSS实例 每个CSS样式由两个组成部分:选择器和…...

MySql创建索引
在MySQL中,可以使用CREATE INDEX语句来创建索引。以下是创建索引的基本语法: CREATE INDEX index_name ON table_name (column1, column2, ...);其中,index_name是索引的名称,可以自定义(也可以不指定索引名称&#x…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
