C语言青蛙跳台阶【图文详解】

青蛙跳台阶
- 前言
- 1. 题目介绍
- 2. 解题思路
- 3. 利用图片来演示青蛙跳台阶的原理
- 4. 如何用C语言实现青蛙跳台阶
前言
在本文,我们要与一只活泼可爱的小青蛙合作,带领着它跳上台阶,这个小家伙精力充沛,特别擅长于跳跃。我们要让它做我们的思维助手,看看有多少种方法让它跳到指定的台阶上。
本文比较生动有趣,没有太多的理论,小青蛙也非常敬业,相信对你来说,阅读本文将是一个愉快的经历,如果有什么建议,可以评论留言我,恒川都会认真看的哦。
我还得温馨地提醒一下你:
本文易懂(不难),但还是值得琢磨的。有些思维方法乍一眼看起来很像,代码写出来似乎也差不多,但是它们之间的解题方法,确实有差别的,你可能需要仔细体会,才能领悟。
如果想看汉诺塔的讲解,请点击该链接汉诺塔详细图解。
1. 题目介绍
一只青蛙可以一次跳 1 级台阶或一次跳 2 级台阶,例如:跳上第一级台阶只有一种跳法:直接跳 1 级即可。跳上两级台阶,有两种跳法: 每次跳 1 级,跳两次; 或者一次跳 2 级.
问要跳上第 n 级台阶有多少种跳法?
2. 解题思路
此类求多少种可能性 的题目一般都有递推性质 ,跟斐波那契,汉诺塔的题型相似,即 f(n)和 f(n-1)…f(1)之间是有联系的。
如果想看汉诺塔的讲解,请点击该链接汉诺塔详细图解
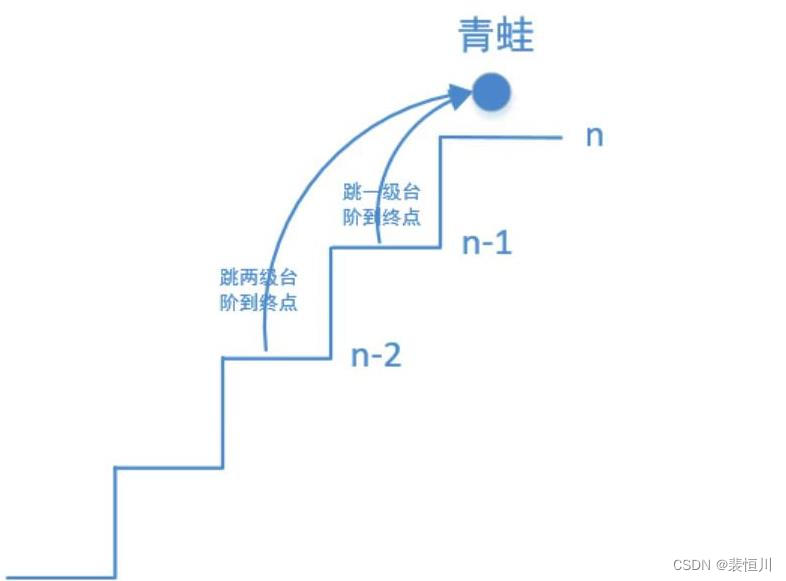
设跳上 n级台阶有 f(n)种跳法。在所有跳法中,青蛙的最后一步只有两种情况: 跳上1级或 2级台阶。
当为 1级台阶: 剩 n-1个台阶,此情况共有 f(n-1)种跳法;
当为 2级台阶: 剩 n-2个台阶,此情况共有 f(n-2)种跳法。
f(n)为以上两种情况之和,即 f(n)=f(n-1)+f(n-2),以上递推性质为斐波那契数列。本题可转化为求斐波那契数列第 n项的值 ,与斐波那契数列等价,唯一的不同在于起始数字不同。
青蛙跳台阶问题: f(0)=1 , f(1)=1, f(2)=2;
斐波那契数列问题: f(0)=0 , f(1)=1, f(2)=1。

斐波那契数列的定义是 f(n + 1) = f(n) + f(n - 1),生成第n项的做法有以下几种:
递归法:
原理: 把 f(n)问题的计算拆分成 f(n-1)和 f(n-2)两个子问题的计算,并递归,以 f(0)和 f(1)为终止条件。
缺点: 大量重复的递归计算,例如 f(n)和 f(n - 1)两者向下递归都需要计算 f(n - 2)的值。
记忆化递归法:
原理: 在递归法的基础上,新建一个长度为 n的数组,用于在递归时存储 f(0)至 f(n)的数字值,重复遇到某数字时则直接从数组取用,避免了重复的递归计算。
缺点: 记忆化存储的数组需要使用 O(N)的额外空间。
动态规划:
原理: 以斐波那契数列性质 f(n + 1) = f(n) + f(n - 1)为转移方程。
从计算效率、空间复杂度上看,动态规划是本题的最佳解法。
链接:https://leetcode-cn.com/problems/qing-wa-tiao-tai-jie-wen-ti-lcof/solution/mian-shi-ti-10-ii-qing-wa-tiao-tai-jie-wen-ti-dong/
来源:力扣(LeetCode)
3. 利用图片来演示青蛙跳台阶的原理


4. 如何用C语言实现青蛙跳台阶
#include<stdio.h>
int dance_s(int n)
{if (n == 1){return 1;//当只有一层台阶时直接返回1}if (n == 2){return 2;//当只有2层台阶时直接返回2}if (n > 2){return dance_s(n - 1) + dance_s(n - 2);}//当n>2时,利用递归,直到结束停止
}
int main()
{int n = 0;scanf("%d", &n);//输入台阶的个数int num = dance_s(n);printf("%d\n", num);//打印共有多少种跳台阶的方案return 0;
}
如果这份博客对大家有帮助,希望各位给恒川一个免费的点赞作为鼓励,并评论收藏一下,谢谢大家!!!
制作不易,如果大家有什么疑问或给恒川的意见,欢迎评论区留言。
相关文章:

C语言青蛙跳台阶【图文详解】
青蛙跳台阶前言1. 题目介绍2. 解题思路3. 利用图片来演示青蛙跳台阶的原理4. 如何用C语言实现青蛙跳台阶前言 在本文,我们要与一只活泼可爱的小青蛙合作,带领着它跳上台阶,这个小家伙精力充沛,特别擅长于跳跃。我们要让它做我们的…...
——list容器的基础理论知识)
笔记(五)——list容器的基础理论知识
list容器是一个双向链表容器,可以高效地进行插入删除元素,但是不能随机存取元素(不支持at()和[]操作符)。一、list容器的对象构造方法list对象采用模板类的默认构造形式例如list<T> lst;#include<iostream>…...

浅谈网络中接口幂等性设计问题
所谓幂等性设计,就是说,一次和多次请求某一个资源应该具有同样的副作用。用数学的语言来表达就是:f(x) f(f(x))。 在数学里,幂等有两种主要的定义。 在某二元运算下,幂等元素是指被自己重复运算(或对于函数…...
《C Primer Plus》第13章复习题与编程练习
《C Primer Plus》第13章复习题与编程练习复习题1. 下面的程序有什么问题?2. 下面的程序完成什么任务?(假设在命令行环境中运行)3. 假设程序中有下列语句:4. 编写一个程序,不接受任何命令行参数或接受一个命…...

计算机SCI论文应该怎么作图? - 易智编译EaseEditing
计算机SCI论文,作图时要注意以下几个方面的问题: 1.图片的格式要tiff或者eps; 2.文件大小不能超过10M; 3.长和宽也给出了具体要求; 4.色彩模式要RGB或者灰度图; 5.文中的文字字体和大小; …...
【一】kubernetes集群部署
一、docker环境搭建 1、移除以前docker相关包 sudo yum remove docker docker-client docker-client-latest docker-common docker-latest docker-latest-logrotate docker-logrotate docker-engine2、配置yam源 sudo yum install -y yum-utilssudo yum-config-manager --ad…...

Docker安装Redis
一、拉取镜像 命令::docker pull <镜像名称>:<版本号> docker pull redis 二:Docker挂载配置文件 挂载:即将宿主的文件和容器内部目录相关联,相互绑定,在宿主机内修改文件的话也随之修改容…...
 系统执行的过程)
在shell中执行一条可执行程序(./a.out) 系统执行的过程
目录 系统调度过程 用户空间角度: 内核角度 1、调用fork创建一个新进程 2、使用_fo_fork创建新进程 3、父进程调用wake_up_new_task尝试唤醒新进程 4、CPU选择一个合适的进程来运行; 5、运行新进程 6、实现负载均衡 系统调度过程 分析在命令行…...
【ArcGIS Pro二次开发】(10):属性表字段(field)的修改
在ArcGIS Pro中,经常会遇到用字段计算器对要素的属性表进行计算。下面以一个例子演示如何在ArcGIS Pro SDK二次开发中实现。 一、要实现的功能 如上图所示的要素图层,要实现如下功能: 当字段【市级行政区】的值为【泉州市】时,将…...

数据结构与算法—散列表
目录 散列表 散列函数 散列冲突解决 1、开放寻址法 1.1 线性探测 1.2 二次探测 1.3 双重散列 2、链表法 使用场景 单词查找 散列表与链表的结合使用LRU 散列表总结 散列表实例 散列表 Word 单词拼写功能,如何实现的?散列表(Has…...

计算机网络笔记、面试八股(一)—— TCP/IP网络模型
本章目录1. TCP/IP网络模型1.1 应用层1.1.1 应用层作用1.1.2 应用层有哪些常用协议1.2 运输层1.2.1 TCP与UDP的区别1.2.2 分块传输1.2.3 端口1.3 网络层1.3.1 IP报文1.3.2 IP地址1.3.3 网络号和主机号的获得1.3.4 子网掩码的获得1.3.5 路由1.3.6 IP地址与MAC地址的区别1.3.7 AR…...
:国际化)
Servlet笔记(18):国际化
三个概念 国际化: 意义着一个网站提供不同版本的翻译成访问者的语言或国籍的内容。本地化: 意味着向网站添加资源,以使其适应特定的地理或文化区域。区域设置: 针对某个国家的某个地区的设置。 Servlet可以根据请求者的区域设置…...

kibana搭建(windowslinux)
1.说明 搭建kibana方便查询es库,本文分别对windows和linux版本进行安装,因为es集群版本是7.4.1,所以配套的kibana也是选择相同版本 2.下载 https://artifacts.elastic.co/downloads/kibana/kibana-7.4.1-windows-x86_64.zip https://artifact…...
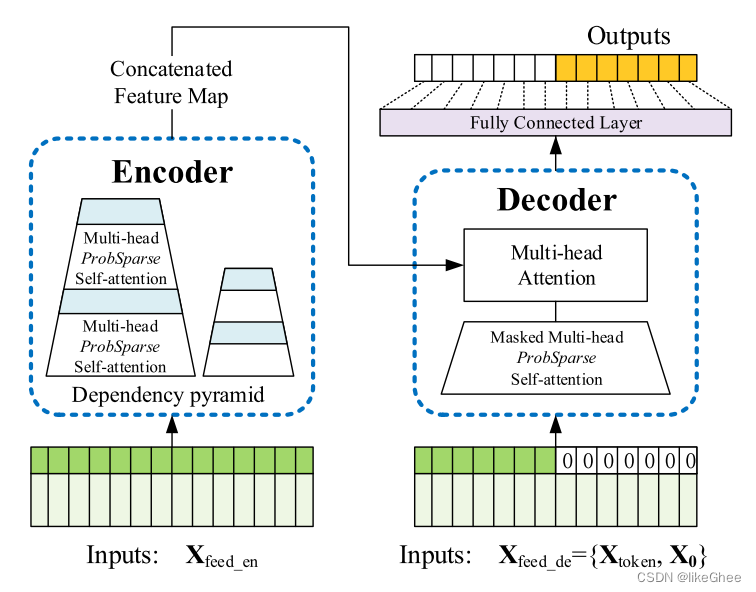
(pytorch进阶之路)Informer
论文:Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting (AAAI’21 Best Paper) 看了一下以前的论文学习学习,我也是重应用吧,所以代码部分会比较多,理论部分就一笔带过吧 论文作者也很良心的…...
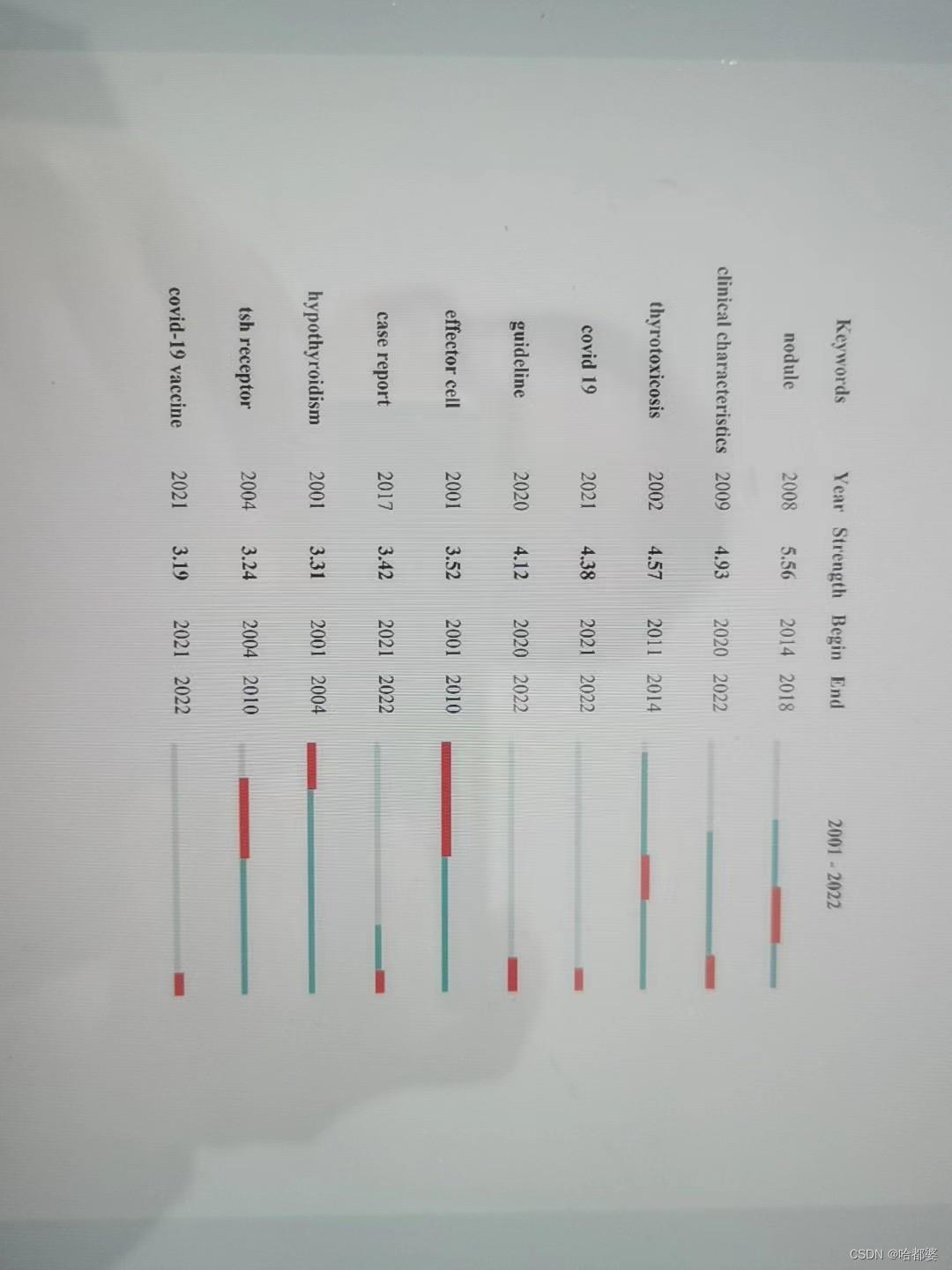
关键词聚类和凸现分析-实战1——亚急性甲状腺炎的
审稿人问题第8页第26行-请指出#是什么意思,并解释为什么亚急性甲状腺炎在这里被列为#8。我认为在搜索亚急性甲状腺炎相关文章时,关键词共现分析应该提供关键词共现的数据。这些结果的实际用途是什么?亚急性甲状腺炎是一种较为罕见但重要的甲状腺疾病&am…...

二叉树——二叉搜索树中的众数
二叉搜索树中的众数 链接 给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。 如果树中有不止一个众数,可以按 任意顺序 返回。 假定…...
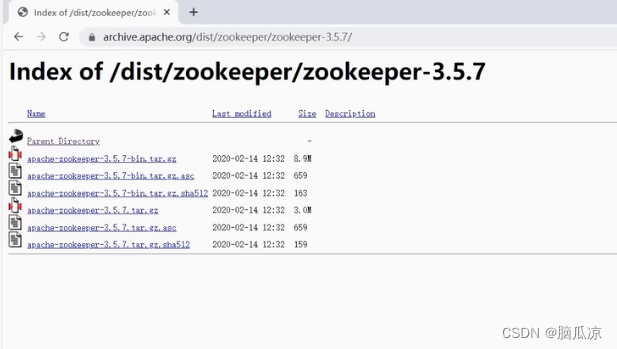
安装_配置参数解读_集群安装配置_启动选举_搭建启停脚本---大数据之ZooKeeper工作笔记004
这里首先下载zookeeper安装包,可以看到官网地址 找到download 点击下载 找到老一点的,我们找3.5.7 in the archive 点击 然后这里找到3.5.7这一个 然后下载这个-bin.tar.gz这个...
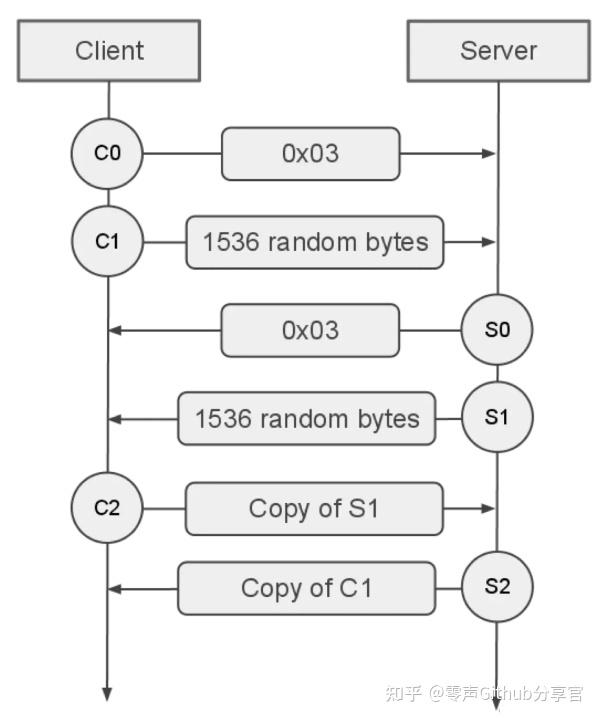
RTMP的工作原理及优缺点
一.什么是RTMP?RTMP(Real-Time Messaging Protocol,实时消息传输协议)是一种用于低延迟、实时音视频和数据传输的双向互联网通信协议,由Macromedia(后被Adobe收购)开发。RTMP的工作原理是&#…...

【数据结构与算法】——第八章:排序
文章目录1、基本概念1.1 什么是排序1.2 排序算法的稳定性1.3 排序算法的分类1.4 内排序的方法2、插入排序2.1 直接插入排序2.2 直接插入排序2.3 希尔排序3、交换排序3.1 冒泡排序3.2 快速排序4、选择排序4.1 简单选择排序4.2 树形选择排序4.3 堆排序4.4 二路归并排序5、基数排序…...

在linux中web服务器的搭建与配置
以下涉及到的linux命令大全查阅 https://www.runoob.com/linux/linux-command-manual.htmlvim命令查阅 https://www.runoob.com/linux/linux-vim.htmlscp命令https://www.runoob.com/linux/linux-comm-scp.html首先要有一个请求的服务地址用ssh 进入到linux系统中ssh 请求的服务…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
