【数据结构(七)】查找算法
文章目录
- 查找算法介绍
- 1. 线性查找算法
- 2. 二分查找算法
- 2.1. 思路分析
- 2.2. 代码实现
- 2.3. 功能拓展
- 3. 插值查找算法
- 3.1. 前言
- 3.2. 相关概念
- 3.3. 实例应用
- 4. 斐波那契(黄金分割法)查找算法
- 4.1. 斐波那契(黄金分割法)原理
- 4.2. 实例应用
查找算法介绍
在 java 中,我们常用的查找有四种:
① 顺序(线性)查找
② 二分查找/折半查找
③ 插值查找
④ 斐波那契查找
1. 线性查找算法
问题:
数组arr[] = {1, 9, 11, -1, 34, 89},使用线性查找方式,找出11所在的位置。
代码实现:
package search;public class SeqSearch {public static void main(String[] args) {int arr[] = { 1, 9, 11, -1, 34, 89 };// 没有顺序的数组int index = seqSearch(arr, 11);if (index == -1) {System.out.println("没有找到");} else {System.out.println("找到了,下标为:" + index);}}/*** 这里实现的线性查找是找到一个满足条件的值,就返回* * @param arr* @param value* @return*/public static int seqSearch(int[] arr, int value) {// 线性查找是逐一比对,发现有相同的值,就返回下标for (int i = 0; i < arr.length; i++) {if (arr[i] == value) {return i;}}return -1;}}
运行结果:

2. 二分查找算法
问题:
请对一个有序数组进行二分查找 {1,8, 10, 89, 1000, 1234} ,输入一个数看看该数组是否存在此数,并且求出下标,如果没有就提示"没有这个数"。
2.1. 思路分析
二分查找的思路分析
-
首先,确定该数组的中间的下标: m i d = ( l e f t + r i g h t ) / 2 mid = (left + right) / 2 mid=(left+right)/2
-
然后让需要查找的数
findVal和arr[mid]比较
2.1.findVal > arr[mid],说明你要查找的数在mid的右边, 因此需要递归的向右查找
2.2.findVal < arr[mid],说明你要查找的数在mid的左边, 因此需要递归的向左查找
2.3.findVal == arr[mid],说明找到,就返回 -
什么时候需要结束递归:
①找到就结束递归
②递归完整个数组,仍然没有找到findVal,也需要结束递归 当left > right就需要退出
2.2. 代码实现
注意:使用二分查找的前提是 该数组是有序的
package search;public class BinarySearch {public static void main(String[] args) {int arr[] = { 1, 8, 10, 89, 1000, 1234 };int resIndex = binarySearch(arr, 0, arr.length - 1, 1);System.out.println("resIndex= " + resIndex);}// 二分查找法/*** * @param arr 数组* @param left 左边的索引* @param right 右边的索引* @param findVal 要查找的值* @return 如果找到就返回下标,如果没有找到就返回-1*/public static int binarySearch(int[] arr, int left, int right, int findVal) {// 当left > right 时,说明递归整个数组,但是没有找到if (left > right) {return -1;}int mid = (left + right) / 2;int midVal = arr[mid];if (findVal > midVal) {// 向右递归return binarySearch(arr, mid + 1, right, findVal);} else if (findVal < midVal) {return binarySearch(arr, left, mid - 1, findVal);} else {return mid;}}}
运行结果:

2.3. 功能拓展
问题:
数组{1,8, 10, 89, 1000, 1000,1234}, 当一个有序数组中,有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000。
代码实现:
package search;import java.util.ArrayList;
import java.util.List;public class BinarySearch {public static void main(String[] args) {int arr[] = { 1, 8, 10, 89, 1000, 1000, 1234 };List<Integer> resIndexList = binarySearch2(arr, 0, arr.length - 1, 1000);System.out.println("resIndexList = " + resIndexList);}/** 思路分析:* 1. 在找 mid 的索引值,不要马上返回* 2. 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 3. 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 4. 将 ArrayList 返回*/public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal) {// 当left > right 时,说明递归整个数组,但是没有找到if (left > right) {return new ArrayList<Integer>();}int mid = (left + right) / 2;int midVal = arr[mid];if (findVal > midVal) {// 向右递归return binarySearch2(arr, mid + 1, right, findVal);} else if (findVal < midVal) {return binarySearch2(arr, left, mid - 1, findVal);} else {/** 思路分析:* 1. 在找 mid 的索引值,不要马上返回* 2. 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 3. 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 4. 将 ArrayList 返回*/List<Integer> resIndexlist = new ArrayList<Integer>();// 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayListint temp = mid - 1;while (true) {if (temp < 0 || arr[temp] != findVal) {// 退出break;}// 否则,就将temp放入到resIndexlistresIndexlist.add(temp);temp -= 1;// temp左移}resIndexlist.add(mid);// 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayListtemp = mid + 1;while (true) {if (temp > arr.length - 1 || arr[temp] != findVal) {// 退出break;}// 否则,就将temp放入到resIndexlistresIndexlist.add(temp);temp += 1;// temp左移}return resIndexlist;}}}
运行结果:

3. 插值查找算法
3.1. 前言
二分查找算法存在查找效率较慢的情况,因为其中的mid是从中间开始取的。假如对数组{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 }进行查找,查找 1 所在的位置,实现代码如下:
package search;import java.util.ArrayList;
import java.util.List;public class BinarySearch {public static void main(String[] args) {int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 };List<Integer> resIndexList = binarySearch2(arr, 0, arr.length - 1, 1);System.out.println("resIndexList = " + resIndexList);}/** 思路分析:* 1. 在找 mid 的索引值,不要马上返回* 2. 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 3. 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 4. 将 ArrayList 返回*/public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal) {System.out.println("调用了一次");// 当left > right 时,说明递归整个数组,但是没有找到if (left > right) {return new ArrayList<Integer>();}int mid = (left + right) / 2;int midVal = arr[mid];if (findVal > midVal) {// 向右递归return binarySearch2(arr, mid + 1, right, findVal);} else if (findVal < midVal) {return binarySearch2(arr, left, mid - 1, findVal);} else {/** 思路分析:* 1. 在找 mid 的索引值,不要马上返回* 2. 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 3. 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 4. 将 ArrayList 返回*/List<Integer> resIndexlist = new ArrayList<Integer>();// 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayListint temp = mid - 1;while (true) {if (temp < 0 || arr[temp] != findVal) {// 退出break;}// 否则,就将temp放入到resIndexlistresIndexlist.add(temp);temp -= 1;// temp左移}resIndexlist.add(mid);// 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayListtemp = mid + 1;while (true) {if (temp > arr.length - 1 || arr[temp] != findVal) {// 退出break;}// 否则,就将temp放入到resIndexlistresIndexlist.add(temp);temp += 1;// temp左移}return resIndexlist;}}}
运行结果:
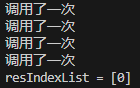
总共调用了4次才查找出1的索引值,效率较慢。通过插值查找可改善上述问题。
3.2. 相关概念
原理介绍:
插值查找算法类似于二分查找,不同的是插值查找每次从自适应 mid 处开始查找。
mid的计算公式:
对二分查找中的求 mid 索引的公式进行修改:

上图公式中:
① low 表示左边索引 left
② high 表示右边索引 right
③ key 就是前面二分查找中讲的 findVal(要查找的值)
即插值查找的 mid计算公式:
m i d = l o w + ( h i g h − l o w ) k e y − a r r [ l o w ] a r r [ h i g h ] − a r r [ l o w ] \begin{aligned} &mid = low + (high-low)\frac{key-arr[low]}{arr[high]-arr[low]} \end{aligned} mid=low+(high−low)arr[high]−arr[low]key−arr[low]
对应前面的代码公式,即:
m i d = l e f t + ( r i g h t – l e f t ) f i n d V a l – a r r [ l e f t ] a r r [ r i g h t ] – a r r [ l e f t ] \begin{aligned} &mid = left + (right – left)\frac{findVal – arr[left]}{arr[right] – arr[left]} \end{aligned} mid=left+(right–left)arr[right]–arr[left]findVal–arr[left]
举例说明:
数组 arr = [1, 2, 3, …, 100]
①假如需要查找的值是 1
(使用二分查找的话,需要多次递归,才能找到 1 的下标0)
使用插值查找算法:
m i d = l e f t + ( r i g h t – l e f t ) f i n d V a l – a r r [ l e f t ] a r r [ r i g h t ] – a r r [ l e f t ] \begin{aligned}&mid = left + (right – left)\frac{findVal – arr[left]}{arr[right] – arr[left]}\end{aligned} mid=left+(right–left)arr[right]–arr[left]findVal–arr[left]
即:
m i d = 0 + ( 99 − 0 ) 1 − 1 100 − 1 = 0 + 99 ∗ 0 99 = 0 ( 直接定位到下标 0 ) \begin{aligned}&mid = 0+(99-0)\frac{1-1}{100-1} = 0 + 99 * \frac{0}{99} = 0\ \ \ (直接定位到下标0)\end{aligned} mid=0+(99−0)100−11−1=0+99∗990=0 (直接定位到下标0)
②假如需要查找的值是 100
m i d = 0 + ( 99 − 0 ) 100 − 1 ( 100 − 1 = 0 + 99 ∗ 99 99 = 0 + 99 = 99 ( 直接定位到下标 99 ) \begin{aligned}&mid =0 + (99 - 0)\frac{100 - 1}{(100 - 1} = 0 + 99 * \frac{99}{99} = 0 + 99 = 99\ \ \ (直接定位到下标99)\end{aligned} mid=0+(99−0)(100−1100−1=0+99∗9999=0+99=99 (直接定位到下标99)
3.3. 实例应用
问题:
对数组 arr = [1, 2, 3, …, 100] ,使用插值查找算法,找到 1 的索引值(下标)
代码实现:
package search;import java.util.Arrays;public class InsertValueSearch {public static void main(String[] args) {int[] arr = new int[100];for (int i = 0; i < 100; i++) {arr[i] = i + 1;}int index = insertValueSearch(arr, 0, arr.length - 1, 1);System.out.println("index = " + index);// System.out.println(Arrays.toString(arr));}// 编写插值查找算法// 说明:插值查找算法也要求数组是有序的/*** * @param arr 数组* @param left 左边索引* @param right 右边索引* @param findVal 要查找的值* @return 如果找到,就返回对应的下标;如果没有找到,就返回-1*/public static int insertValueSearch(int[] arr, int left, int right, int findVal) {System.out.println("查找了一次");// 注意:findVal < arr[0] 和 findVal > arr[arr.length - 1] 必须需要,否则得到的mid可能越界if (left > right || findVal < arr[0] || findVal > arr[arr.length - 1]) {return -1;}// 求出 midint mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);int midVal = arr[mid];if (findVal > midVal) {// 说明应该向右边递归return insertValueSearch(arr, mid + 1, right, findVal);} else if (findVal < midVal) {// 说明应该向左递归return insertValueSearch(arr, left, mid - 1, findVal);} else {return mid;}}}
运行结果:
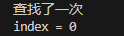
注意事项:
- 对于数据量较大,关键字分布比较均匀的查找表来说,采用插值查找, 速度较快.
- 关键字分布不均匀的情况下,该方法不一定比折半(二分)查找要好
4. 斐波那契(黄金分割法)查找算法
黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。取其前三位数字的近似值是 0.618。由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。这是一个神奇的数字,会带来意想不到的效果。
斐波那契数列 {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … … } 发现斐波那契数列的两个相邻数 的比例,无限接近 黄金分割值0.618。
4.1. 斐波那契(黄金分割法)原理
斐波那契查找原理与前两种相似,仅仅改变了中间结点(mid)的位置,mid 不再是中间或插值得到,而是位于黄金分割点附近,即 m i d = l o w + F [ k − 1 ] − 1 mid=low+F[k-1]-1 mid=low+F[k−1]−1( F F F 代表斐波那契数列),如下图所示:

对 F(k-1)-1 的理解:
- 由斐波那契数列 F [ k ] = F [ k − 1 ] + F [ k − 2 ] F[k]=F[k-1]+F[k-2] F[k]=F[k−1]+F[k−2] 的性质,可以得到 ( F [ k ] − 1 ) = ( F [ k − 1 ] − 1 ) + ( F [ k − 2 ] − 1 ) + 1 (F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1 (F[k]−1)=(F[k−1]−1)+(F[k−2]−1)+1 。该式说明:只要顺序表的长度为 F[k]-1,则可以将该表分成长度为 F [ k − 1 ] − 1 F[k-1]-1 F[k−1]−1 和 F [ k − 2 ] − 1 F[k-2]-1 F[k−2]−1 的两段,即如上图所示。从而中间位置为 m i d = l o w + F [ k − 1 ] − 1 mid=low+F[k-1]-1 mid=low+F[k−1]−1
- 类似的,每一子段也可以用相同的方式分割
- 但顺序表长度 n n n 不一定刚好等于 F [ k ] − 1 F[k]-1 F[k]−1,所以需要将原来的顺序表长度 n n n 增加至 F [ k ] − 1 F[k]-1 F[k]−1。这里的 k k k 值只要能使得 F [ k ] − 1 F[k]-1 F[k]−1 恰好大于或等于 n n n 即可,由以下代码得到,顺序表长度增加后,新增的位置(从 n + 1 n+1 n+1 到 F [ k ] − 1 F[k]-1 F[k]−1 位置),都赋为 n n n 位置的值即可。
while(n>fib(k)-1)
k++;
4.2. 实例应用
问题:
请对一个有序数组进行斐波那契查找 {1,8, 10, 89, 1000, 1234} ,输入一个数看看该数组是否存在此数,并且求出下标,如果没有就提示"没有这个数"(return = -1)。
代码实现:
package search;import java.util.Arrays;public class FibonacciSearch {public static int maxSize = 20;public static void main(String[] args) {int[] arr = { 1, 8, 10, 89, 1000, 1234 };System.out.println("index = " + fibSearch(arr, 89));}// 因为后面我们mid=low+F(k-1)-1,需要使用斐波那契数列,因此我们需要先获取到一个斐波那契数列// 非递归方法得到一个斐波那契数列public static int[] fib() {int[] f = new int[maxSize];f[0] = 1;f[1] = 1;for (int i = 2; i < maxSize; i++) {f[i] = f[i - 1] + f[i - 2];}return f;}// 编写斐波那契查找算法// 使用非递归的方式编写算法/*** * @param a 数组* @param key 需要查找的关键字(值)* @return 返回对应的下标,如果没有,就返回-1*/public static int fibSearch(int[] a, int key) {int low = 0;int high = a.length - 1;int k = 0;// 表示斐波那契分割数值的下标int mid = 0;// 存放mid值int f[] = fib();// 获取到斐波那契数列// 获取到斐波那契分割数值的下标while (high > f[k] - 1) {k++;}// 因为f[k]的值 可能大于a的长度,因此需要使用Arrays类,构造一个新的数组,并指向a[]// 不足的部分会使用0填充int[] temp = Arrays.copyOf(a, f[k]);// 实际上,需要使用a数组的最后的数填充temp// 举例:// temp = {1,8,10,89,1000,1234,0,0,0} --> {1,8,10,89,1000,1234,1234,1234,1234}for (int i = high + 1; i < temp.length; i++) {temp[i] = a[high];}// 使用while循环处理,找到keywhile (low <= high) {// 只要这个条件满足,就可以找mid = low + f[k - 1] - 1;if (key < temp[mid]) {// 继续向数组的前面查找(左边)high = mid - 1;// 为什么是k--?// 说明:// 1. 全部元素=前面的元素+后面的元素// 2. f[k] = f[k-1] + f[k-2]// 因为 前面有f[k-1]个元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3]// 即 在f[k-1]的前面继续查找(k--)// 即 下次循环的 mid = f[k-1-1]-1k--;} else if (key > temp[mid]) {// 继续向数组的后面查找(右边)low = mid + 1;// 为什么是 k -= 2// 说明// 1. 全部元素=前面的元素+后面的元素// 2. f[k] = f[k-1] + f[k-2]// 因为 后面有f[k-2]个元素,所以可以继续拆分 f[k-2] = f[k-3] + f[k-4]// 即 在f[k-2]的后面继续查找(k-=2)// 即 下次循环的 mid = f[k-1-2]-1k -= 2;} else {// 找到// 需要确定,返回的是哪一个下标if (mid <= high) {return mid;} else {return high;}}}return -1;}}
运行结果:
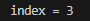
相关文章:
【数据结构(七)】查找算法
文章目录 查找算法介绍1. 线性查找算法2. 二分查找算法2.1. 思路分析2.2. 代码实现2.3. 功能拓展 3. 插值查找算法3.1. 前言3.2. 相关概念3.3. 实例应用 4. 斐波那契(黄金分割法)查找算法4.1. 斐波那契(黄金分割法)原理4.2. 实例应用 查找算法介绍 在 java 中,我们…...
Android画布Canvas绘制drawBitmap基于源Rect和目的Rect,Kotlin
Android画布Canvas绘制drawBitmap基于源Rect和目的Rect,Kotlin <?xml version"1.0" encoding"utf-8"?> <androidx.appcompat.widget.LinearLayoutCompat xmlns:android"http://schemas.android.com/apk/res/android"xmlns…...
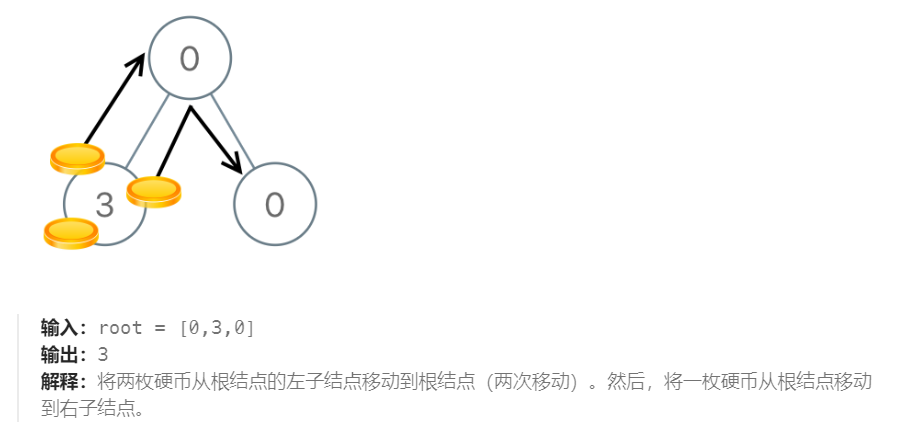
深度优先搜索LeetCode979. 在二叉树中分配硬币
给你一个有 n 个结点的二叉树的根结点 root ,其中树中每个结点 node 都对应有 node.val 枚硬币。整棵树上一共有 n 枚硬币。 在一次移动中,我们可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点。移动可以是从父结点到…...
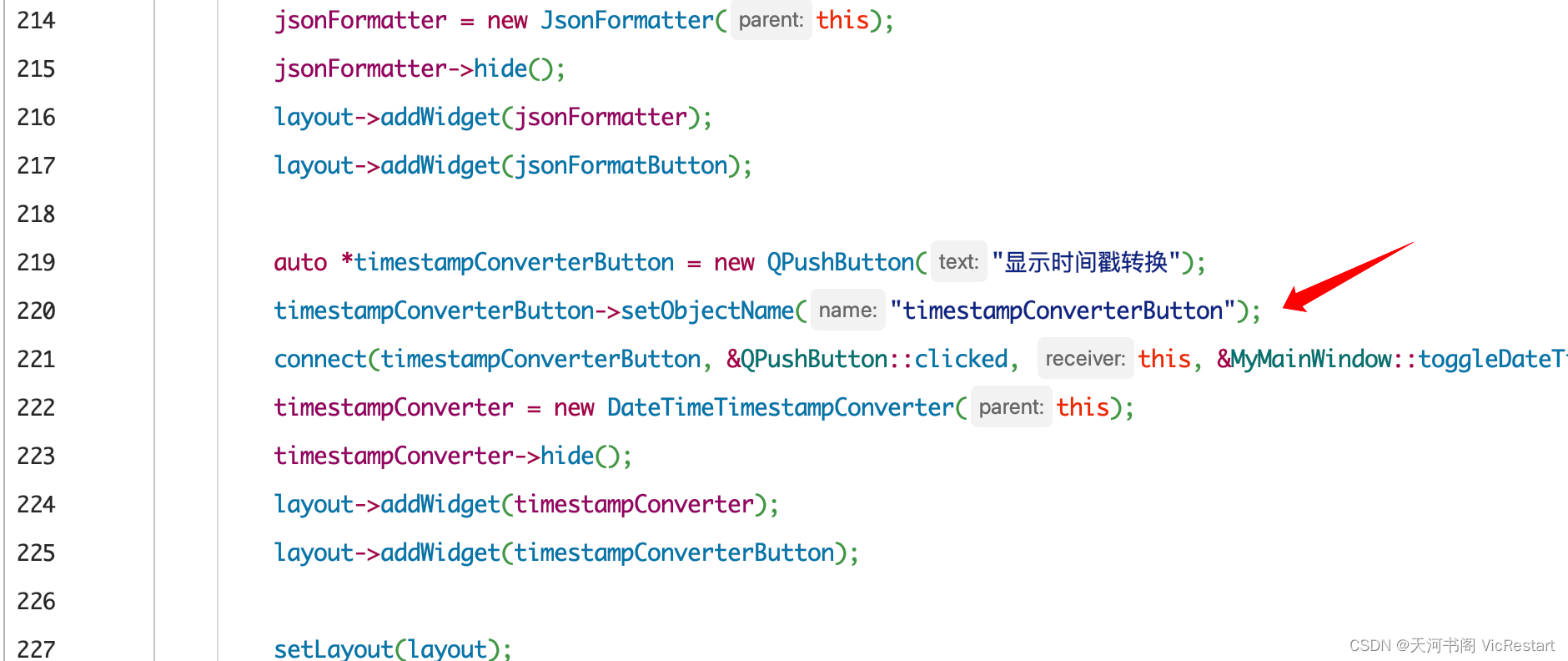
C++学习之路(十)C++ 用Qt5实现一个工具箱(增加一个时间戳转换功能)- 示例代码拆分讲解
上篇文章,我们用 Qt5 实现了在小工具箱中添加了《JSON数据格式化》功能,还是比较实用的。为了继续丰富我们的工具箱,今天我们就再增加一个平时经常用到的功能吧,就是「 时间戳转换 」功能,而且实现点击按钮后文字进行变…...

Linux 5.15安全特性之ARM64 PAC
ARM64 PAC(Pointer Authentication Code)机制是ARM架构中引入的一种安全特性,旨在提供指针的完整性和安全性保护。它通过在指针中插入一段额外的代码进行签名,以验证指针的完整性,从而抵御缓冲区溢出和代码注入等攻击。…...

同旺科技 分布式数字温度传感器
内附链接 1、数字温度传感器 主要特性有: ● 支持PT100 / PT1000 两种铂电阻; ● 支持 2线 / 3线 / 4线 制接线方式; ● 支持5V~17V DC电源供电; ● 支持电源反接保护; ● 支持通讯波特率1200bps、2…...

状态空间的定义
状态空间是描述一个系统所有可能状态的集合。在系统理论、控制论、计算机科学、强化学习等领域,状态空间是一种常见的概念。 状态空间框架是一种用于描述和分析系统的方法,它包括系统的状态、状态之间的转移关系以及与状态相关的行为。下面详细解释状态…...

数据挖掘实战-基于word2vec的短文本情感分析
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

大数据面试总结
1、冒泡排序、选择排序 2、二分查找 3、 hashmap和hashtable的区别?hashmap的底层实现原理? a、hashtable和hashmap的区别: 1、hashtable是线程安全的,会在每一个方法中都添加方法synchronize(同步机制)…...
利大于弊:物联网技术对电子商务渠道的影响
For Better or For Worse: Impacts of IoT Technology in e-Commerce Channel 物联网技术使用传感器和其他联网设备来手机和共享数据,并且被视为一种可以为供应链成员带来巨大的机会的突破性技术。本文的研究背景是:一个提供物联网基础设备的电子商务平…...
)
Python 元组详解(tuple)
文章目录 1 概述1.1 性质1.2 下标1.3 切片 2 常用方法2.1 访问:迭代、根据下标2.2 删除:del2.3 运算符:、*2.4 计算元组中元素个数:len()2.5 返回元组中元素最大值:max()2.6 返回元组中元素最小值:min()2.7…...

Redis部署-主从模式
目录 单点问题 主从模式 解析主从模式 配置redis主从模式 info replication命令查看复制相关的状态 断开复制关系 安全性 只读 传输延迟 拓扑结构 数据同步psync replicationid offset psync运行流程 全量复制流程 无硬盘模式 部分复制流程 积压缓冲区 实时复…...

全栈冲刺 之 一天速成MySQL
一、为什么使用数据库 数据储存在哪里? 硬盘、网盘、U盘、光盘、内存(临时存储) 数据持久化 使用文件来进行存储,数据库也是一种文件,像excel ,xml 这些都可以进行数据的存储,但大量数据操作…...

服务器运行train.py报错解决
在服务器配置完虚拟环境以及安装完各种所需库后,发现报错Traceback (most recent call last): File "/root/yolov5-master/yolov5-master/train.py", line 48, in <module> import val as validate # for end-of-epoch mAP File "/root/yolov5…...

Flutter开发type ‘Future<int>‘ is not a subtype of type ‘int‘ in type cast错误
文章目录 问题描述错误源码 问题分析解决方法修改后的代码 问题描述 今天有个同事调试flutter程序时报错,问我怎么解决,程序运行时报如下错误: type ‘Future’ is not a subtype of type ‘int’ in type cast 错误源码 int order Databas…...
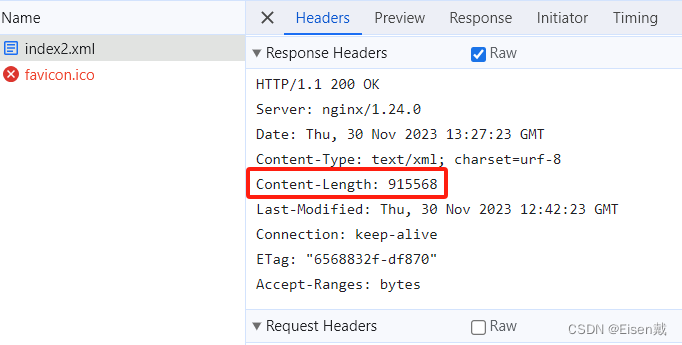
Nginx(十二) gzip gzip_static sendfile directio aio 组合使用测试(2)
测试10:开启gzip、sendfile、aio、directio1m,关闭gzip_static,请求/index.js {"time_iso8601":"2023-11-30T17:20:5508:00","request_uri":"/index.js","status":"200","…...

hls实现播放m3u8视频将视频流进行切片 HLS.js简介
github官网GitHub - video-dev/hls.js: HLS.js is a JavaScript library that plays HLS in browsers with support for MSE.HLS.js is a JavaScript library that plays HLS in browsers with support for MSE. - GitHub - video-dev/hls.js: HLS.js is a JavaScript library …...
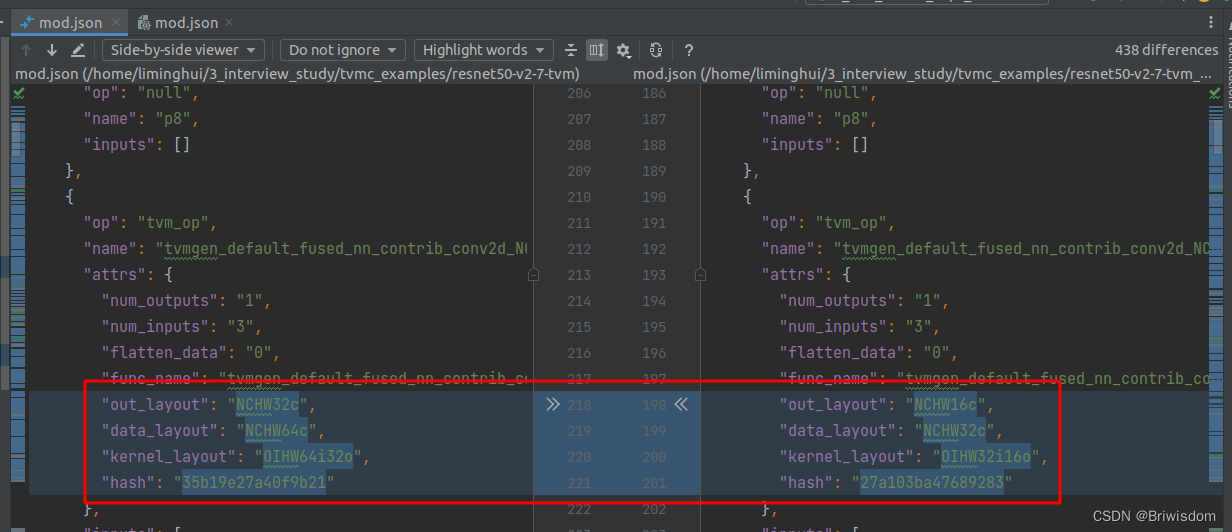
Ubuntu20.04部署TVM流程及编译优化模型示例
前言:记录自己安装TVM的流程,以及一个简单的利用TVM编译模型并执行的示例。 1,官网下载TVM源码 git clone --recursive https://github.com/apache/tvmgit submodule init git submodule update顺便完成准备工作,比如升级cmake版本…...
)
华为OD机试真题-两个字符串间的最短路径问题-2023年OD统一考试(C卷)
题目描述: 给定两个字符串,分别为字符串A与字符串B。例如A字符串为ABCABBA,B字符串为CBABAC可以得到下图m*n的二维数组,定义原点为(0, 0),终点为(m, n),水平与垂直的每一条边距离为1,映射成坐标系如下图。 从原点(0, 0)到(0, A)为水平边,距离为1,从(0, A)到(A, C)为垂…...

python try-except
相比于直接raise ValueError,使用try-except可以使程序在发生异常后仍然能够运行。 在try的部分中,当遇到第一个Error,就跳转到except中寻找对应类型的error,后续代码不再执行,如果try中有多个Error,注意顺…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
