K-means算法通俗原理及Python与R语言的分别实现
K均值聚类方法是一种划分聚类方法,它是将数据分成互不相交的K类。K均值法先指定聚类数,目标是使每个数据到数据点所属聚类中心的总距离变异平方和最小,规定聚类中心时则是以该类数据点的平均值作为聚类中心。
01K均值法原理与步骤
对于有N个数据的数据集,我们想把它们聚成K类,开始需要指定K个聚类中心,假设第i类有ni个样本数据,计算每个数据点分别到聚类中心的距离平方和,距离这里直接用的欧式距离,还有什么海明距离、街道距离、余弦相似度什么的其实都可以,这里聚类的话,欧式距离就好。
(1)、所有类别样本数等于总样本数,即每个类类是互不相同的

(2)、每一类(假设是第i类)中数据点到聚类中心距离平方总和di为:
xi表示第i类各点平均值(聚类中心)
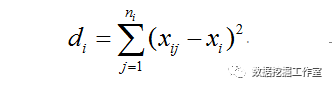
(3)、K类数据点距离之和为:

这样就会有一个KN的距离平方和矩阵,每一列(比如第j列)的最小值对应的行数(比如第i行)就表明:第j个数据样本属于第i类别。这样,每个数据就会分别属于不同的类别了。
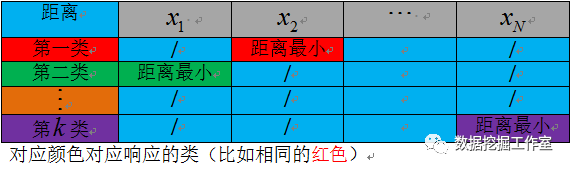
比如,表格中红色部分数据点x2到第一类的聚类中心距离最小,则x2就属于第一类。
K均值步骤:
- 随机选取K个数据点作为(起始)聚类中心;
- 按照距离最近原则分配数据点到对应类;
- 计算每类的数据点平均值(新的聚类中心);
- 计算数据点到聚类中心总距离;
- 如果与上一次相比总距离下降,聚类中心替换;
- 直到总距离不再下降或者达到指定计算次数。
其实,这个过程相对比较简单,给我一组聚类中心,总能根据到聚类中心距离最小原则生成一组聚类方案,然后计算各个类别到聚类中心距离总和是否下降,如果距离总和下降,就继续计算每类数据点平均值(新的聚类中心),对应的聚类方案要好(还是那句话:给我一组聚类中心,总能根据到聚类中心距离最小原则生成一组聚类方案),然后不断计算,直到距离总和下降幅度很小(几乎收敛),或者达到指定计算次数。
K-means算法缺点主要是:
- 对异常值敏感;
- 需要提前确定k值;
- 结果不稳定;
02 K均值算法Python的实现
思路:
- 首先用random模块产生随机聚类中心;
- 用numpy包简化运算;
- 写了一个函数实现一个中心对应一种聚类方案;
- 不断迭代;
- matplotlib包结果可视化。
代码如下:
- import numpy as np
- import random as rd
- import matplotlib.pyplot as plt
- import math
- #数据
- dat = np.array([[14,22,15,20,30,18,32,13,23,20,21,22,23,24,35,18],
- [15,28,18,30,35,20,30,15,25,23,24,25,26,27,30,16]])
- print(dat)
- #聚类中心#
- n = len(dat[0])
- N = len(dat)n
- k = 3
- #-------随机产生-----#
- center = rd.sample(range(n),k)
- center = np.array([dat.T[i] for i in center])
- print(‘初始聚类中心为:’)
- print(center)
- print(‘-----------------------’)
-
- #计算聚类中心
- def cent(x):
- return(sum(x)/len(x))
-
- #计算各点到聚类中心的距离之和
- def dist(x):
- #聚类中心
- m0 = cent(x)
- dis = sum(sum((x-m0)2))
- return(dis)
-
- #距离
- def f(center):
- c0 = []
- c1 = []
- c2 = []
- D = np.arange(k*n).reshape(k,n)
- d0 = center[0]-dat.T
- d1 = center[1]-dat.T
- d2 = center[2]-dat.T
- d = np.array([d0,d1,d2])
- for i in range(k):
- D[i] = sum((d[i]2).T)
- for i in range(n):
- ind = D.T[i].argmin()
- if(ind 0):
- c0.append(i)#分配类别
- else:
- if(ind 1):
- c1.append(i)
- else:
- c2.append(i)
- C0 = np.array([dat.T[i] for i in c0])
- C1 = np.array([dat.T[i] for i in c1])
- C2 = np.array([dat.T[i] for i in c2])
- C = [C0,C1,C2]
- print([c0,c1,c2])
- s = 0
- for i in C:
- s+=dist(i)
- return(s,C)
-
- n_max = 50
- #初始距离和
- print(‘第1次计算!’)
- dd,C = f(center)
- print(‘距离和为’+str(dd))
- print(‘第2次计算!’)
- center = [cent(i) for i in C]
- Dd,C = f(center)
- print(‘距离和为’+str(Dd))
- K = 3
-
- while(K<n_max):
- #两次差值很小并且计算了一定次数
- if(math.sqrt(dd-Dd)<1 and K>20):
- break;
- print(‘第’+str(K)+‘次计算!’)
- dd = Dd
- print(‘距离和为’+str(dd))
- #当前聚类中心
- center = [cent(i) for i in C]
- Dd,C = f(center)
- K+=1
-
-
- #—聚类结果可视化部分—#
-
- j = 0
- for i in C:
- if(j 0):
- plt.plot(i.T[0],i.T[1],‘ro’)
- if(j 1):
- plt.plot(i.T[0],i.T[1],‘b+’)
- if(j == 2):
- plt.plot(i.T[0],i.T[1],‘g*’)
- j+=1
-
- plt.show()
(1):聚类成功的例子:
对于不合适的初始随机聚类中心,一般而言不会失败,成功次数较多。
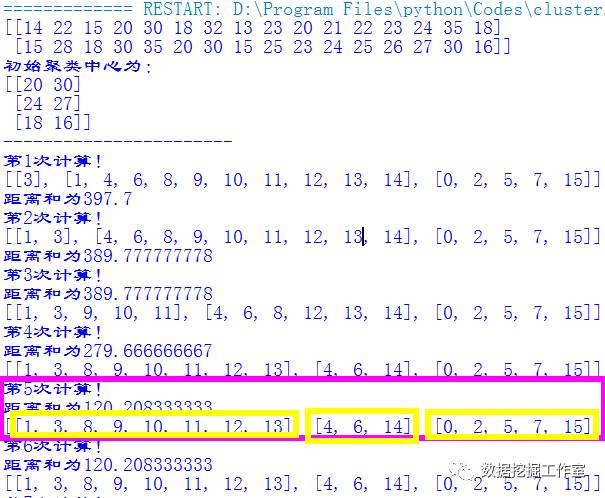
可以看出,其实第五次就收敛了,共分成了三类。它们的标签序号为:
第一类:[1, 3, 8, 9, 10, 11, 12, 13];
第二类:[4, 6, 14];
第三类:[0, 2, 5, 7, 15]
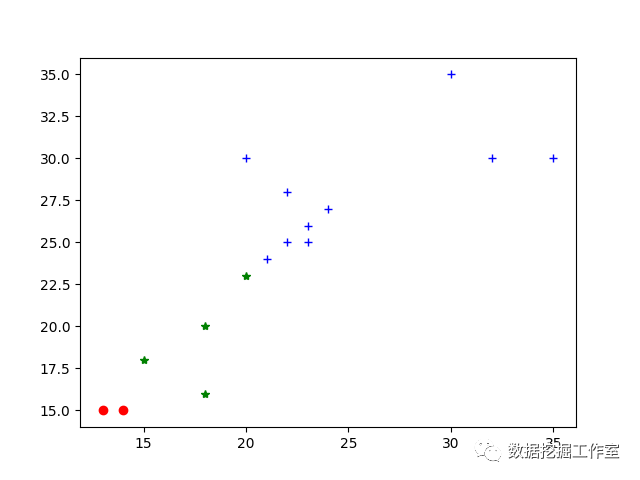
聚类图:

聚类结果与实际情况一致
(2):聚类失败的例子:
有时候可能会失败,运行实验了三次出现了一次败笔,迭代过程如下:

散点图:
聚类失败图
显然,由于初始点的随机选取不当,导致聚类严重失真!这聚类效果明显就很差,表明随机产生的初始聚类中心应该不合适,最后不管怎么迭代,都不可能生成合适的聚类了,这与k-means算法的原理确实可以解释的。这就是k-means的最显著的缺点!
03K均值算法的R语言实现
用的还是上面程序一样的数据,R语言聚类就很方便,直接调用kmeans(data,聚类数)就能方便完成:
- rm(list = ls())
- path <- ‘C:\Users\26015\Desktop\clu.txt’
- dat <- read.csv(path,header = FALSE)
- dat <- t(dat)
- kc <- kmeans(dat,3)
- summary(kc)
- kc
查看聚类结果:
- K-means clustering with 3 clusters of sizes 8, 3, 5
- Cluster means:
- [,1] [,2]
- 1 21.87500 26.00000
- 2 32.33333 31.66667
- 3 15.60000 16.80000
聚成3类,分别有8,3,5个数据
Clustering vector:
V1 V2 V3 V4 V5 V6 V7 V8 V9
3 1 3 1 2 3 2 3 1
V10 V11 V12 V13 V14 V15 V16
1 1 1 1 1 2 3
第一类:2,4,9,10,11,12,13,14
第二类:1,3,6,8,16;
第三类:5,7,15
由于Python下标是从“0”开始,所以两种方法聚类结果实际上是一样的!
相关文章:

K-means算法通俗原理及Python与R语言的分别实现
K均值聚类方法是一种划分聚类方法,它是将数据分成互不相交的K类。K均值法先指定聚类数,目标是使每个数据到数据点所属聚类中心的总距离变异平方和最小,规定聚类中心时则是以该类数据点的平均值作为聚类中心。 01K均值法原理与步骤 对于有N个…...

使用 db2diag 工具来分析 db2diag 日志文件
供数据库和系统管理员使用的主日志文件为管理通知日志。db2diag 日志文件旨在供 IBM 软件支持机构用于进行故障诊断。 管理通知日志消息也以标准化消息格式记录到 db2diag 日志文件。 db2diag 工具用于对 db2diag 日志文件中的大量信息进行过滤和格式化。过滤 db2diag 日志文…...
在Pytorch中使用Tensorboard可视化训练过程
这篇是我对哔哩哔哩up主 霹雳吧啦Wz 的视频的文字版学习笔记 感谢他对知识的分享 本节课我们来讲一下如何在pytouch当中去使用我们的tensorboard 对我们的训练过程进行一个可视化 左边有一个visualizing models data and training with tensorboard 主要是这么一个教程 那么这里…...
Redis 命令全解析之 Hash类型
文章目录 ⛄介绍⛄命令⛄RedisTemplate API⛄应用场景 ⛄介绍 Hash类型,也叫散列,其value是一个无序字典,类似于Java中的 HashMap 结构。 String结构是将对象序列化为JSON字符串后存储,当需要修改对象某个字段时很不方便…...

postgresql数据库配置主从并配置ssl加密
1、先将postgresql数据库主从配置好 参考:postgresql主从配置 2、在主节点配置ssl加密,使用navicat测试是否可以连接 参考:postgresql配置ssl 3、正常连接无误后,将root.crt、server.crt、server.key复制到从数据库节点的存储…...
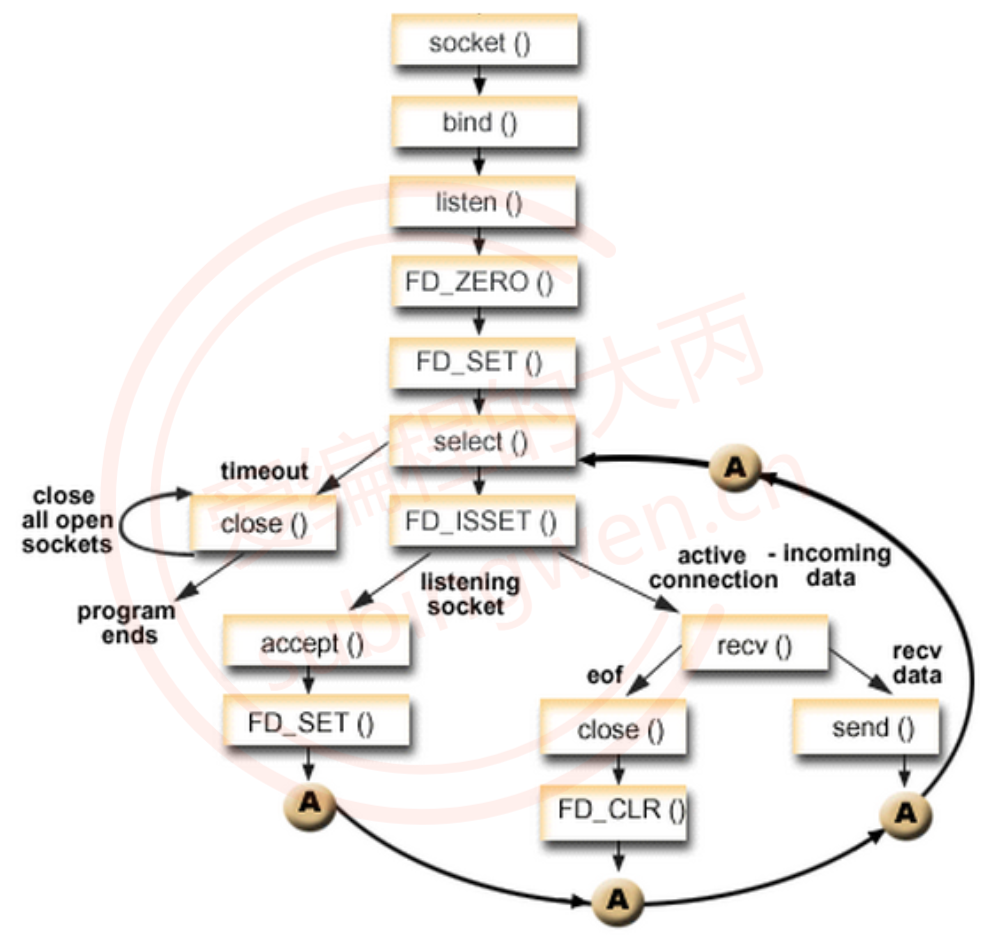
IO多路转接之select
IO多路转接之select 1. IO多路转接(复用)2. select2.1 函数原型2.2 细节描述 3. 并发处理3.1 处理流程3.2 通信代码 原文链接 1. IO多路转接(复用) IO多路转接也称为IO多路复用,它是一种网络通信的手段(机…...
)
linux如何删除大文件的第一行(sed)
可以用sed命令实现: 删除文档的第一行 1. sed -i 1d <file>删除文档的最后一行 1. sed -i $d <file>在文档指定行中增加一行 # 示例如下: echo "1"; echo "2"; echo "4"; echo "5"; # 想要在echo…...
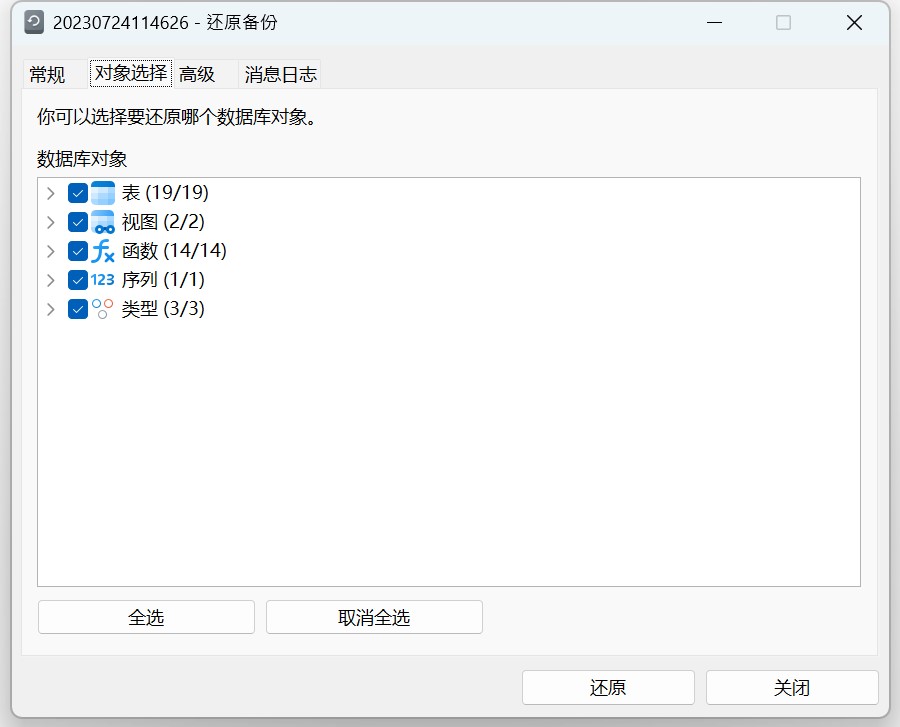
Navicat 技术指引 | 适用于 GaussDB 分布式的备份/还原功能
Navicat Premium(16.3.3 Windows 版或以上)正式支持 GaussDB 分布式数据库。GaussDB 分布式模式更适合对系统可用性和数据处理能力要求较高的场景。Navicat 工具不仅提供可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结…...

【广州华锐互动VRAR】VR戒毒科普宣传系统有效提高戒毒成功率
随着科技的不断发展,虚拟现实(VR)技术已经逐渐渗透到各个领域,为人们的生活带来了前所未有的便利。在教育科普领域,VR技术的应用也日益广泛,本文将详细介绍广州华锐互动开发的VR戒毒科普宣传系统࿰…...

守护安全,六氟化硫气体泄漏报警装置校准服务
在电力工业中,六氟化硫(SF6)气体是一种重要的介质,它用作封闭式中、高压开关的灭弧和绝缘气体。六氟化硫气体的卓越性能实现了装置经济化、低维护化的操作。与普通装置相比,可以节省最多90%的空间。 六氟化…...
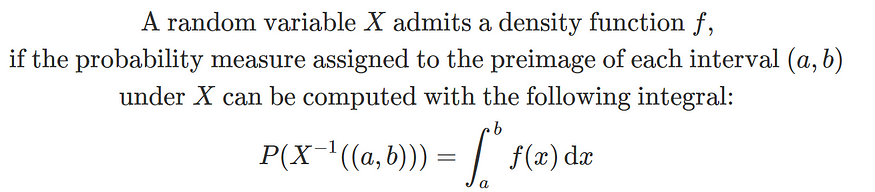
概率测度理论方法(第 2 部分)
一、说明 欢迎回到这个三部曲的第二部分!在第一部分中,我们为测度论概率奠定了基础。我们探索了测量和可测量空间的概念,并使用这些概念定义了概率空间。在本文中,我们使用测度论来理解随机变量。 作为一个小回顾,在第…...
实战:Docker Compose 下 Nginx、Java、Mysql 和 Redis 服务协同部署(包含解决浏览器访问Linux部署服务器本地资源问题)
1. 背景 在该实战中,我们将探讨如何使用Docker Compose协同部署Nginx、Java、Mysql和Redis服务,实现一个视频上传与展示的应用。具体需求如下: Java应用负责上传视频和图片资源到Nginx目录下,作为资源服务器。Nginx服务作为静态…...

Docker 设置国内镜像源
Docker 设置国内镜像源 您可以通过修改daemon配置文件/etc/docker/daemon.json来使用加速器 具体配置如下: {"registry-mirrors" : ["https://registry.docker-cn.com","http://hub-mirror.c.163.com","https://docker.mirro…...

通信协议 远程调用RPC
1.通讯协议 所有的HDFS通讯协议都是建立在TCP/IP协议之上。 客户端通过一个可配置的TCP端口连接到Namenode,通过ClientProtocol协议与Namenode交 互。而Datanode使用DatanodeProtocol协议与Namenode交互。 一个远程过程调用(RPC)模型被抽象出来封装ClientProtoc…...
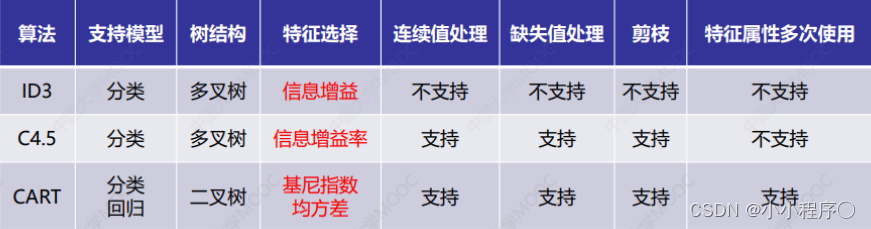
决策树 算法原理
决策树 算法原理 决策树的原理 决策树: 从训练数据中学习得出一个树状结构的模型 决策树属于判别模型 决策树是一种树状结构,通过做出一系列决策 (选择) 来对数据进行划分,这类似于针对一系列问题进行选择。 决策树的决策过程就是从根节点开始&#…...

Git全局设置命令---设置提交人邮箱
介绍 使用git命令设置提交人邮箱。 命令 git config --global user.email "xxxxxxxx.com"...

3DCAT+上汽奥迪:打造新零售汽车配置器实时云渲染解决方案
在 5G、云计算等技术飞速发展的加持下,云渲染技术迎来了突飞猛进的发展。在这样的背景下,3DCAT应运而生,成为了业内知名的实时云渲染服务商之一。 交互式3D实时云看车作为云渲染技术的一种使用场景,也逐步成为一种新的看车方式&a…...
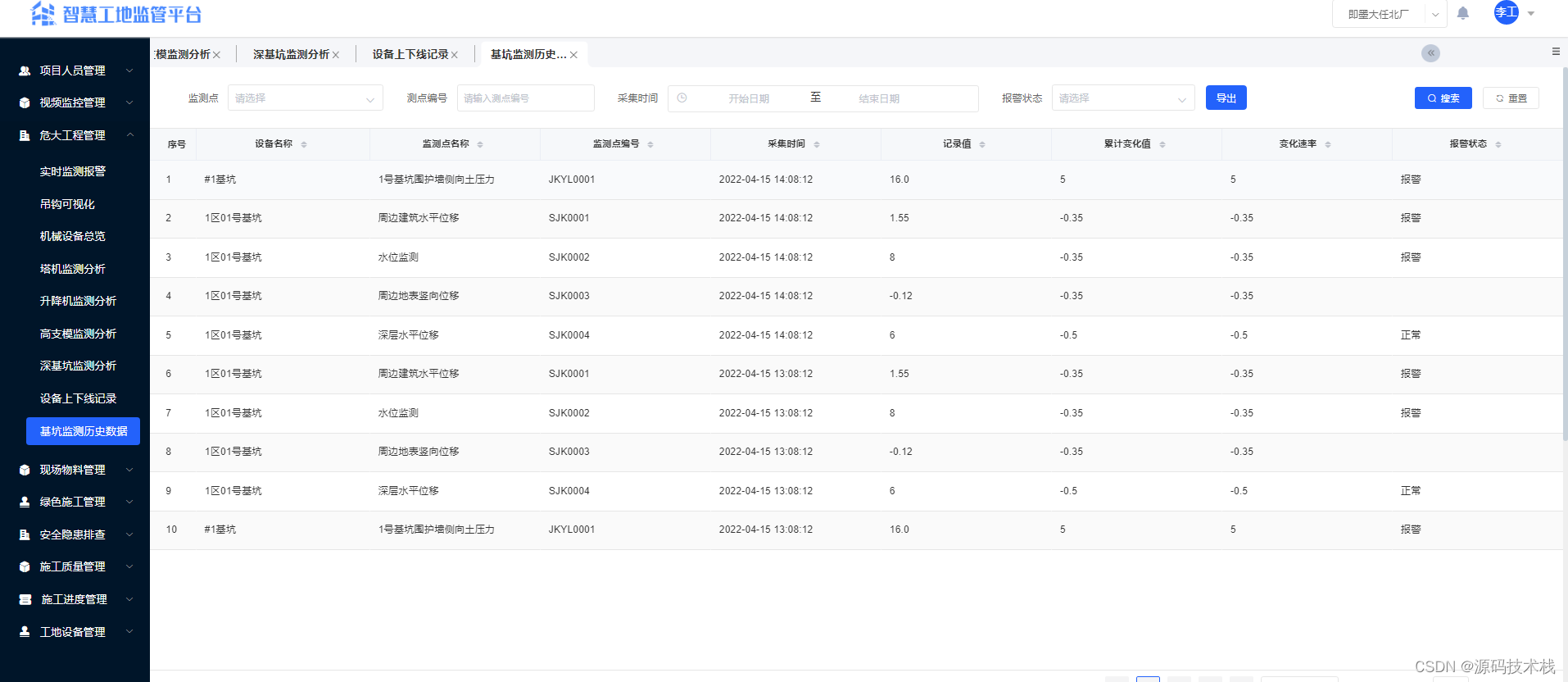
物联网+AI智慧工地云平台源码(SaaS模式)
智慧工地云平台充分运用数字化技术,聚焦施工现场岗位一线,依托物联网、互联网、AI等技术,围绕施工现场管理的人、机、料、法、环五大维度,以及施工过程管理的进度、质量、安全三大体系为基础应用,实现全面高效的工程管…...

python打开相机,用鼠标左键框选矩形区域,支持一次框选多个矩形区域,通过鼠标右标清除上一次画的矩形。
方案一 import cv2# Global variables rectangles [] current_rectangle [] drawing False# Mouse callback function def mouse_callback(event, x, y, flags, param):global rectangles, current_rectangle, drawingif event cv2.EVENT_LBUTTONDOWN:drawing Truecurren…...

卷积之后通道数为什么变了
通道数增多与卷积之后得到的图像特征数量有关 卷积层的作用本来就是把输入中的特征分离出来变成新的 feature map,每一个输出通道就是一个卷积操作提取出来的一种特征。在此过程中ReLU激活起到过滤的作用,把负相关的特征点去掉,把正相关的留…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
