Codeforces Round 768 (Div. 1) D. Flipping Range(思维题 等价类性质 dp)
题目

思路来源
官方题解
洛谷题解
题解
可操作的最短区间长度肯定是gcd,记为g,然后考虑如何dp
考虑g个等价类,每个等价类i,i+g,i+2*g,...
每次翻转长度为g的区间,会同时影响到g个等价类总的翻转的奇偶性,
性质一:只有每个等价类翻的次数奇偶性相同才合法
性质二:此外,翻1-g和翻2-g+1可以起到翻(1,g+1)效果
等价类内翻两个相邻的,可以类似地叠加成两个不相邻的,推广为(i,i+x*g)
即等价类内如果有偶数个负数,可以两两翻完,奇数个负数,可以剩一个
此外,可以一开始翻一次[1,g],改变每个等价类内负数个数的奇偶性,所以两种情况都考虑
也就是考虑将所有数都翻成正数,
然后按是否操作一次[1,g],决定在等价类内负数个数为奇/偶时将绝对值最小的数回退掉,减掉2倍mn
这就是性质解法
而dp做法,则是注意到性质一后dp即可,dp[i][j]表示i的等价类的数总共被翻了奇/偶次
枚举当前数翻还是不翻,翻的话加1次翻,算-a[i],否则加0次翻,算a[i],
对每个等价类内dp值求和,取翻奇/偶次二者的max
代码1(性质)
// Problem: D. Flipping Range
// Contest: Codeforces - Codeforces Round 768 (Div. 1)
// URL: https://codeforces.com/contest/1630/problem/D
// Memory Limit: 256 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=1e6+10;
int t,n,m,g,v,a[N];
ll dp[N][2];
//考虑等价类 当前等价类内被翻了奇/偶次 只有每个等价类翻的次数奇偶性相同才合法
//翻1-k和翻2-k+1可以起到翻(1,k+1)效果 类似地 可以翻(i,i+x*k)
void sol(){sci(n),sci(m); ll all=0;rep(i,0,n-1){sci(a[i]);all+=abs(a[i]);}int g=0;rep(i,1,m){sci(v);g=__gcd(g,v);}ll sum1=0,sum2=0;rep(i,0,g-1){int mn=2e9,cnt=0;for(int j=i;j<n;j+=g){mn=min(mn,abs(a[j]));cnt+=(a[j]<0);}if(cnt&1)sum1+=mn;else sum2+=mn;}printf("%lld\n",all-2ll*min(sum1,sum2));
}
int main(){sci(t); // t=1while(t--){sol();}return 0;
}代码2(dp)
// Problem: D. Flipping Range
// Contest: Codeforces - Codeforces Round 768 (Div. 1)
// URL: https://codeforces.com/contest/1630/problem/D
// Memory Limit: 256 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=1e6+10;
int t,n,m,g,v,a[N];
ll dp[N][2];
//考虑等价类 当前等价类内被翻了奇/偶次 只有每个等价类翻的次数奇偶性相同才合法
//翻1-k和翻2-k+1可以起到翻(1,k+1)效果 类似地 可以翻(i,i+x*k)
void sol(){sci(n),sci(m); rep(i,0,n-1){sci(a[i]);}int g=0;rep(i,1,m){sci(v);g=__gcd(g,v);}ll sum1=0,sum2=0;rep(i,0,g-1){dp[i][0]=0;dp[i][1]=-2e9;for(int j=i;j<n;j+=g){ll x1=dp[i][0],x2=dp[i][1];dp[i][0]=max(x1+a[j],x2-a[j]);dp[i][1]=max(x1-a[j],x2+a[j]);}sum1+=dp[i][0];sum2+=dp[i][1];}printf("%lld\n",max(sum1,sum2));
}
int main(){sci(t); // t=1while(t--){sol();}return 0;
}相关文章:

Codeforces Round 768 (Div. 1) D. Flipping Range(思维题 等价类性质 dp)
题目 思路来源 官方题解 洛谷题解 题解 可操作的最短区间长度肯定是gcd,记为g,然后考虑如何dp 考虑g个等价类,每个等价类i,ig,i2*g,... 每次翻转长度为g的区间,会同时影响到g个等价类总的翻转的奇偶性, 性质一&…...

springboot集成kafka消费数据
springboot集成kafka消费数据 文章目录 springboot集成kafka消费数据1.引入pom依赖2.添加配置文件2.1.添加KafkaConsumerConfig.java2.2.添加KafkaIotCustomProperties.java2.3.添加application.yml配置 3.消费者代码 1.引入pom依赖 <dependency><groupId>org.spri…...

单例模式---JAVA
目录 “饿汉”模式 完整代码 “懒汉”模式 完整代码 单例模式:保证某个类在程序中只存在唯一一份实例, 而不会创建出多个实例。 单例模式可以通过实例创建的时间来分为两种:“饿汉”和“懒汉”模式。 “饿汉”模式 所谓的“饿汉”模式实则就是在类…...
maven管理使用
maven基本使用 一、简介二、配置文件三、项目结构maven基本标签实践(例子) 四、pom插件配置五、热部署六、maven 外部手动加载jar打包方式Maven上传私服或者本地 一、简介 基于Ant 的构建工具,Ant 有的功能Maven 都有,额外添加了其他功能.本地仓库:计算机中一个文件夹,自己定义…...

如何在一个系统中同时访问异构的多种数据库
如何在一个系统中同时访问异构的多种数据库 比如在一个系统中,要同时访问MySQL,H2, MsAccess, Mongodb. 要是使用Hibernate, MyBatis这些ORM,难度简直不敢想像。 要是MySQL还使用了分库分表,那更加不得了,一大堆的组件都要配合着…...
)
半监督学习 - 半监督聚类(Semi-Supervised Clustering)
什么是机器学习 半监督聚类是一种集成了有标签数据和无标签数据的聚类方法,其目标是在聚类的过程中利用有标签数据的信息来提高聚类性能。在半监督聚类中,一部分数据集有已知的标签,而另一部分没有标签。 以下是半监督聚类的基本思想和一些…...
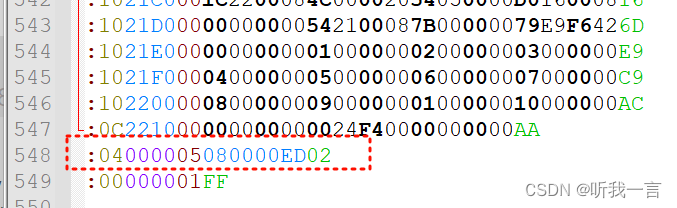
实现STM32烧写程序-(3) Hex文件结构
简介 要对STM32进行更新动作, 就需要对程序文件进行解析, 大部分编译的生成程序文件是Hex或者Bin, 先来看看Hex的结构吧。 资料 Hex文件 简介 Hex文件格式最早由Intel公司于1973年创建。它最初是为了在Intel 8080微处理器上存储和传输二进制数据而设计的。随后,Hex…...
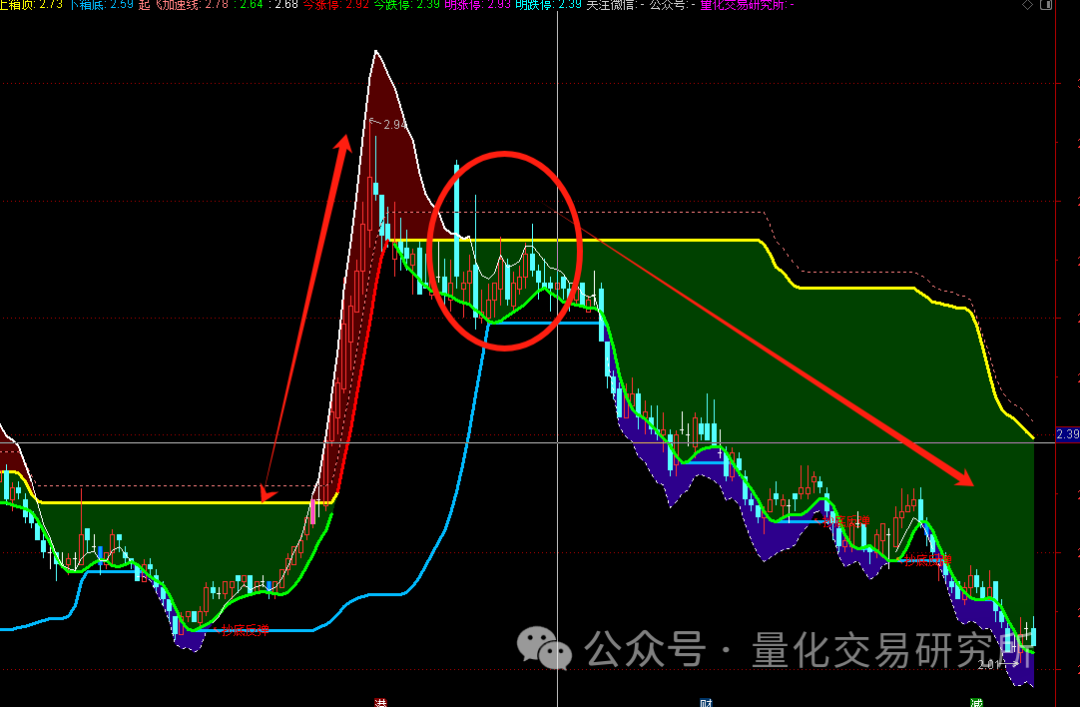
精品量化公式——“区域突破”,应对当下行情较好的主图看盘策略
不多说,直接上效果如图: ► 日线表现 代码评估 技术指标代码评估: VAR1, VAR2, VAR3:这些变量是通过指数移动平均(EMA)计算得出的。EMA是一种常用的技术分析工具,用于平滑价格数据并减少市场“…...

自然语言处理5——发掘隐藏规律 - Python中的关联规则挖掘
目录 写在开头1. 了解关联规则挖掘的概念和实际应用1.1 关联规则挖掘在市场分析和购物篮分析中的应用1.2 关联规则的定义和基本原理1.3 应用场景2. 使用Apriori算法和FP-growth算法进行关联规则挖掘2.1 Apriori算法的工作原理和实现步骤2.2 FP-growth算法的优势和使用方法2.3 A…...

【记录】重装系统后的软件安装
考完研重装了系统,安装软件乱七八糟,用到什么装什么。在这里记录一套标准操作,备用。一个个装还是很麻烦,我为什么不直接写个脚本直接下载安装包呢?奥,原来是我太菜了还不会写脚本啊!先记着吧&a…...
- ACodec(七))
Android 13 - Media框架(31)- ACodec(七)
之前的章节中我们解了 input buffer 是如何传递给 OMX 的,以及Output buffer 是如何分配并且注册给 OMX 的。这一节我们就来看ACodec是如何处理OMX的Callback的。 1、OMXNodeInstance Callback 这一节我们只大致记录Callback是如何传递给ACodec的。在之前的学习中我…...

快速了解VR全景拍摄技术运用在旅游景区的优势
豆腐脑加了糖、烤红薯加了勺,就连索菲亚大教堂前都有了“人造月亮”,在这个冬季,“尔滨”把各地游客宠上了天。面对更多的游客无法实地游玩,哈尔滨冰雪世界再添新玩法,借助VR全景拍摄技术对冬季经典冰雪体验项目进行全…...

分布形态的度量_峰度系数的探讨
集中趋势和离散程度是数据分布的两个重要特征,但要全面了解数据分布的特点,还应掌握数据分布的形态。 描述数据分布形态的度量有偏度系数和峰度系数, 其中偏度系数描述数据的对称性,峰度系数描述与正态分布的偏离程度。 峰度系数反映分布峰的尖峭程度的重要指标. 当…...
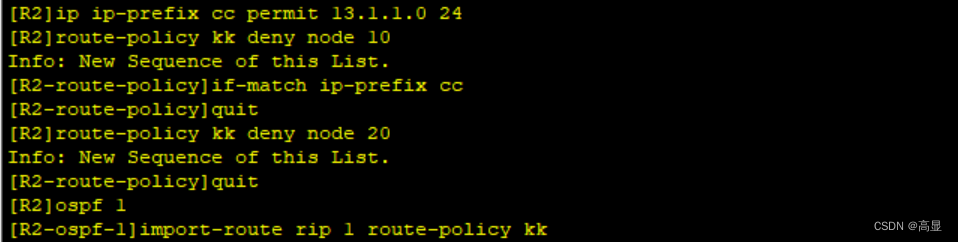
HCIP 重发布
拓扑图&IP划分如下: 第一步,配置接口IP&环回地址 以R1为例,R2~R4同理 interface GigabitEthernet 0/0/0 ip address 12.1.1.1 24 interface GigabitEthernet 0/0/1 ip address 13.1.1.1 24 interface LoopBack 0 ip address 1.1.1.…...

FX图中的节点代表什么操作
在 FX 图中,每个节点代表一个操作。这些操作可以是函数调用、方法调用、模块实例调用,也可以是 torch.nn.Module 实例的调用。每个节点都对应一个调用站点,如运算符、方法和模块。 一.节点操作 下面是一些节点可能代表的操作: 1…...

【Java 设计模式】创建型之单例模式
文章目录 1. 定义2. 应用场景3. 代码实现1)懒汉式2)饿汉式 4. 应用示例结语 在软件开发中,单例模式是一种常见的设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式在需要控制某些资源,如数…...
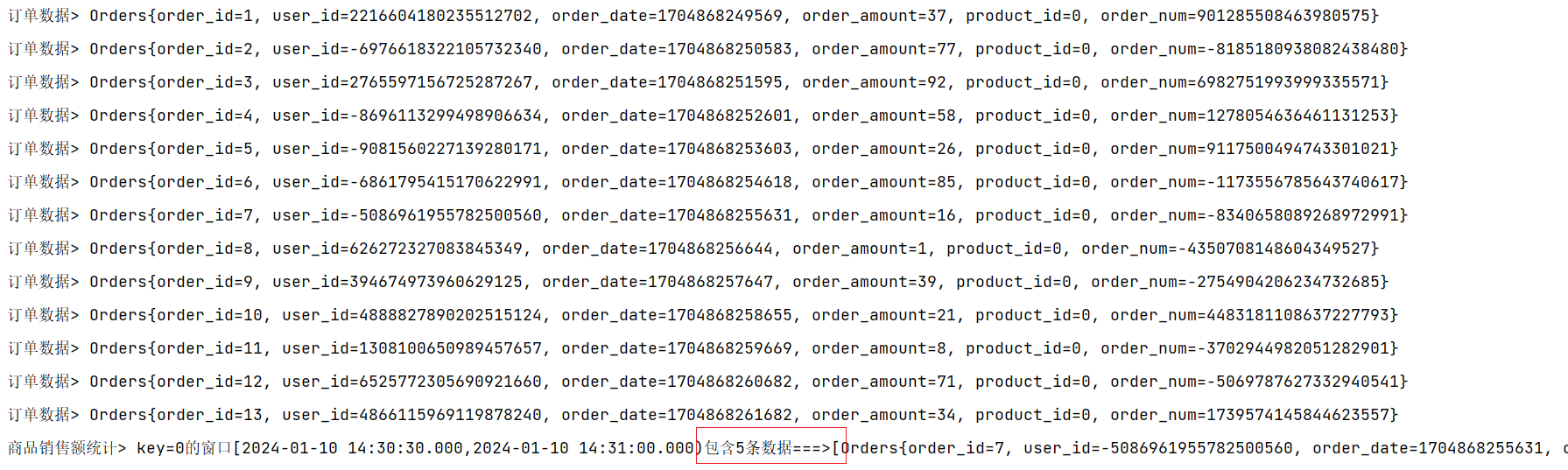
FlinkAPI开发之窗口(Window)
案例用到的测试数据请参考文章: Flink自定义Source模拟数据流 原文链接:https://blog.csdn.net/m0_52606060/article/details/135436048 窗口的概念 Flink是一种流式计算引擎,主要是来处理无界数据流的,数据源源不断、无穷无尽。…...
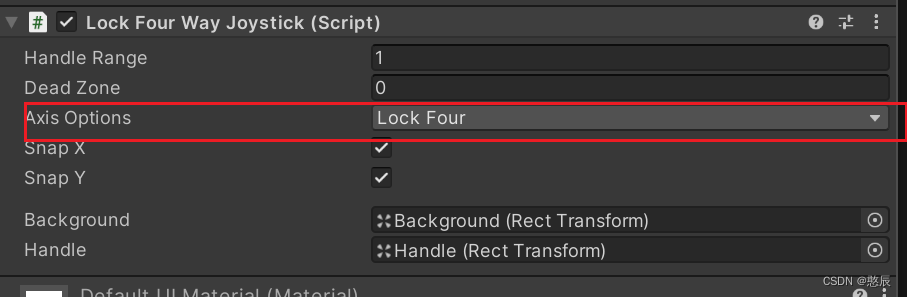
【Unity】Joystick Pack摇杆插件实现锁四向操作
Joystick Pack 简介:一款Unity摇杆插件,非常轻量化 摇杆移动类型:圆形、横向、竖向 摇杆类型: Joystick描述Fixed固定位置Floating浮动操纵杆从用户触碰的地方开始,一直固定到触碰被释放。Dynamic动态操纵…...

29 旋转工具箱
效果演示 实现了一个菜单按钮的动画效果,当鼠标悬停在菜单按钮上时,菜单按钮会旋转315度,菜单按钮旋转的同时,菜单按钮旋转的8个小圆圈也会依次旋转360度,并且每个小圆圈的旋转方向和菜单按钮的旋转方向相反࿰…...
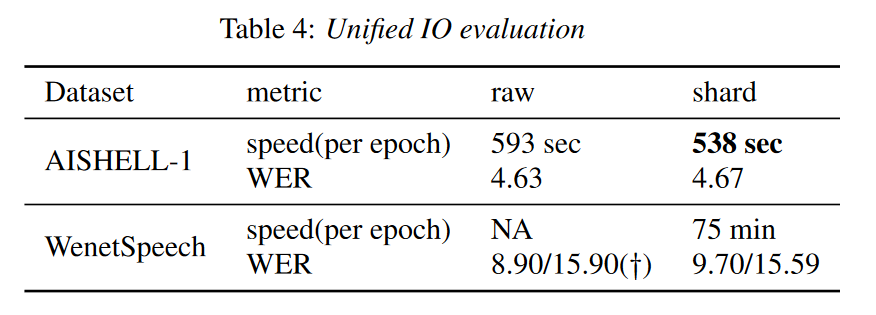
WeNet2.0:提高端到端ASR的生产力
摘要 最近,我们提供了 WeNet [1],这是一个面向生产(工业生产环境需求)的端到端语音识别工具包,在单个模型中,它引入了统一的两次two-pass (U2) 框架和内置运行时(built-in runtime)…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
