【算法】最短路计数(搜索)复习
题目
给出一个 N 个顶点 M 条边的无向无权图,顶点编号为 1 到 N。
问从顶点 1 开始,到其他每个点的最短路有几条。
输入格式
第一行包含 2 个正整数 N,M,为图的顶点数与边数。
接下来 M 行,每行两个正整数 x,y,表示有一条顶点 x 连向顶点 y 的边,请注意可能有自环与重边。
输出格式
输出 N 行,每行一个非负整数,第 i 行输出从顶点 1 到顶点 i 有多少条不同的最短路,由于答案有可能会很大,你只需要输出对 100003 取模后的结果即可。
如果无法到达顶点 i 则输出 0。
数据范围
1≤N≤1e5
1≤M≤2e5
输入样例:
5 7
1 2
1 3
2 4
3 4
2 3
4 5
4 5
输出样例:
1
1
1
2
4思路
变量介绍:

从点1出发,开始搜索设每条边的长度为1。
=========================================================================
如果从点 t 到达点 u 时,所走的路径长度小于dist[ u ],则进行

将点 u 的cnt[ u ] 更新为cnt[ t ],dist[ u ] 更新为 dist[ t ] + 1。
=========================================================================
如果从点 t 到达点 u 时,所走的路径长度等于 dist[ u ],则进行

将cnt[t] 加到 cnt[u] 上面。
=========================================================================
如果从点 t 到达点 u 时,所走的路径长度大于 dist[ u ],则不进行任何操作。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 100100, M = 4 * N;
int n,m;
int h[N],ne[M],e[M],idx;
int dist[N],cnt[N];
bool st[N];void add(int a,int b)
{ne[idx] = h[a],e[idx] = b,h[a] = idx ++;
}void bfs()
{memset(dist,0x3f,sizeof dist);queue<int> q;cnt[1] = 1;dist[1] = 0;q.push(1);st[1] = true;while(!q.empty()){int t = q.front();st[t] = false;q.pop();for(int i = h[t]; ~i; i = ne[i]){int u = e[i];if(dist[u] > dist[t] + 1){dist[u] = dist[t] + 1;cnt[u] = cnt[t];cnt[u] %= 100003;if(!st[u]) q.push(u);}else if(dist[u] == dist[t] + 1){cnt[u] += cnt[t];cnt[u] %= 100003;}}}
}int main()
{cin >> n >> m;memset(h,-1,sizeof h);while(m --){int a,b;cin >> a >> b;add(a,b);add(b,a);}bfs();for(int i = 1; i <= n; i ++) printf("%d\n",cnt[i]);return 0;
}| 难度:中等 |
| 时/空限制:1s / 64MB |
| 总通过数:6250 |
| 总尝试数:11237 |
| 来源:《信息学奥赛一本通》 |
| 算法标签 最短路 方案数 |
题目来自: 1134. 最短路计数 - AcWing题库
相关文章:

【算法】最短路计数(搜索)复习
题目 给出一个 N 个顶点 M 条边的无向无权图,顶点编号为 1 到 N。 问从顶点 1 开始,到其他每个点的最短路有几条。 输入格式 第一行包含 2 个正整数 N,M,为图的顶点数与边数。 接下来 M 行,每行两个正整数 x,y,表…...
html火焰文字特效
下面是代码: <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>HTML5火焰文字特效DEMO演示</title><link rel"stylesheet" href"css/style.css" media"screen" type&quo…...
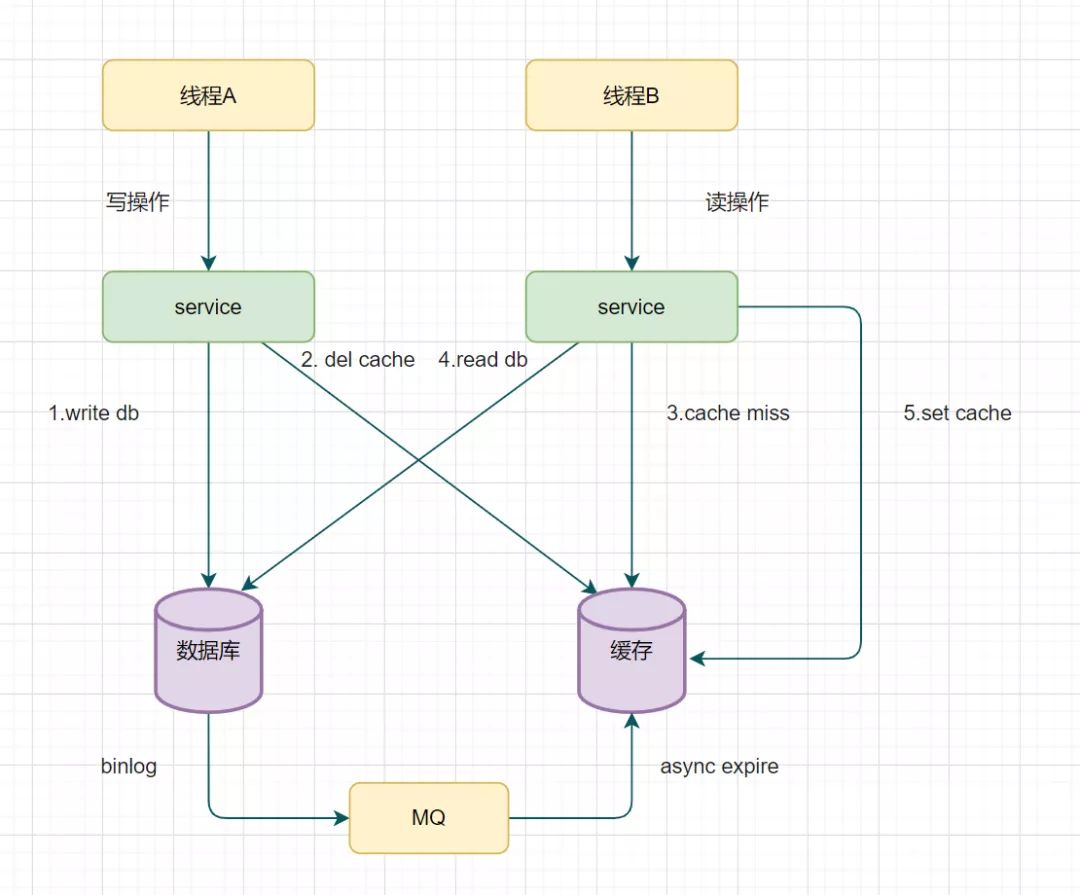
Redis双写一致性
所有的情况都是再并发情况下存在温蒂 一、先更新数据库,再更新缓存场景-不推荐 当有两个线程A、B,同时对一条数据进行操作,一开始数据库和redis的数据都为1,当线程A去修改数据库,将1改为2,然后线程A在修改…...

html+css+javascript实现贪吃蛇游戏
文章目录 一、贪吃蛇游戏二、JavaScript三、HTML四、CSS五、热门文章 一、贪吃蛇游戏 这是一个简单的用HTML、CSS和JavaScript实现的贪吃蛇游戏示例。 HTML部分: <!DOCTYPE html> <html> <head><title>贪吃蛇游戏</title><styl…...

【K8S】Kubernetes 中滚动发布由浅入深实战
目录 一、Kubernetes中滚动发布的需求背景1.1 滚动发布1.2 滚动发布、蓝绿发布、金丝雀发布的区别 二、Kubernetes中实现滚动发布2.1 定义Kubernetes中的版本2.2 创建 Deployment 资源对象2.2.1 在 Yaml 中定义 Deployment 资源对象2.2.2 执行命令创建 Deployment 资源对象 三、…...
MSP430仿真器使用常见问题
一、 主要是驱动安装问题 有用户反应驱动安装不上,按照用户手册操作一直不能安装成功。 可以尝试如下步骤进行安装。 1. 双击设备管理器中无法安装或者提示有错误的430仿真器设备 选择驱动程序——更新驱动程序 选择手动安装 选择从电脑设备驱动列表中安装 弹出下…...
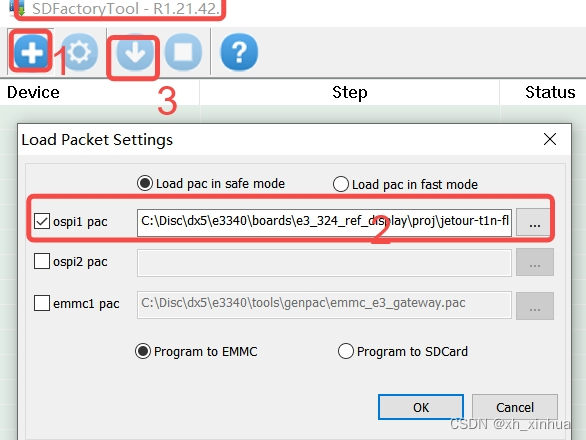
芯驰E3340软件编译以及更新步骤
打开已有工程File->Open Solution: 东南项目:e3340\boards\e3_324_ref_display\proj\jetour-t1n-fl3\sf\SES 编译:build->build sf 增加头文件和宏定义: 编译完成sf后,进行编译bootloader 东南项目:e3340\boa…...

HCIA——18实验:NAT
学习目标: NAT 学习内容: NAT 1.要求——基本的 2.模型 3.IP分配、规划、优化 1)思路 R2为ISP路由器,其上只能配置ip地址,不得冉进行其他的任何配置—ospf配置 认证 、汇总、沉默接口、加快收敛、缺省路由 PC1-PC2…...

在VBA中使用SQL
VBA在处理大量的数据/计算时如果使用常规方法会比较慢,因此需要对其进行性能优化以提高运行速度,一般的方法是数组计算或者sql计算。SQL计算的速度最快,限制也是最多的,数组速度其次,灵活性也更高 如果要在vba中调用sql处理数据基本可以遵循一个套路,只要修改其中的SQL语…...
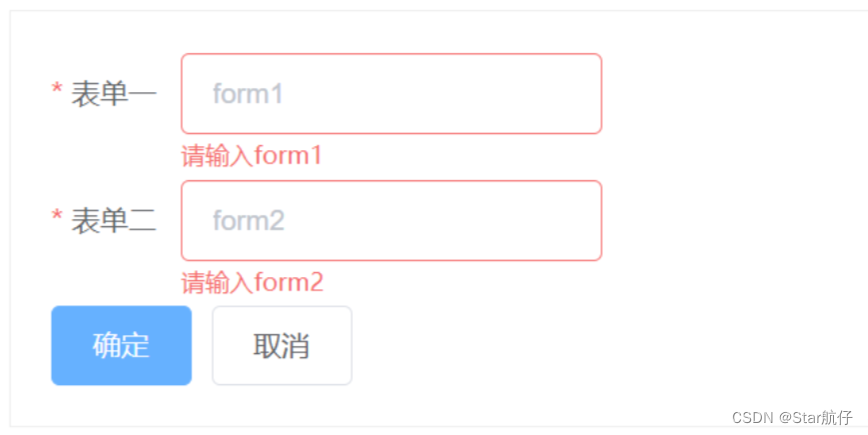
vue项目中使用Element多个Form表单同时验证
一、项目需求 在项目中一个页面中需要实现多个Form表单,并在页面提交时需要对多个Form表单进行校验,多个表单都校验成功时才能提交。 二、实现效果 三、多个表单验证 注意项:多个form表单,每个表单上都设置单独的model和ref&am…...
自然语言处理--概率最大中文分词
自然语言处理附加作业--概率最大中文分词 一、理论描述 中文分词是指将中文句子或文本按照语义和语法规则进行切分成词语的过程。在中文语言中,词语之间没有明显的空格或标点符号来分隔,因此需要通过分词工具或算法来实现对中文文本的分词处理。分词的…...
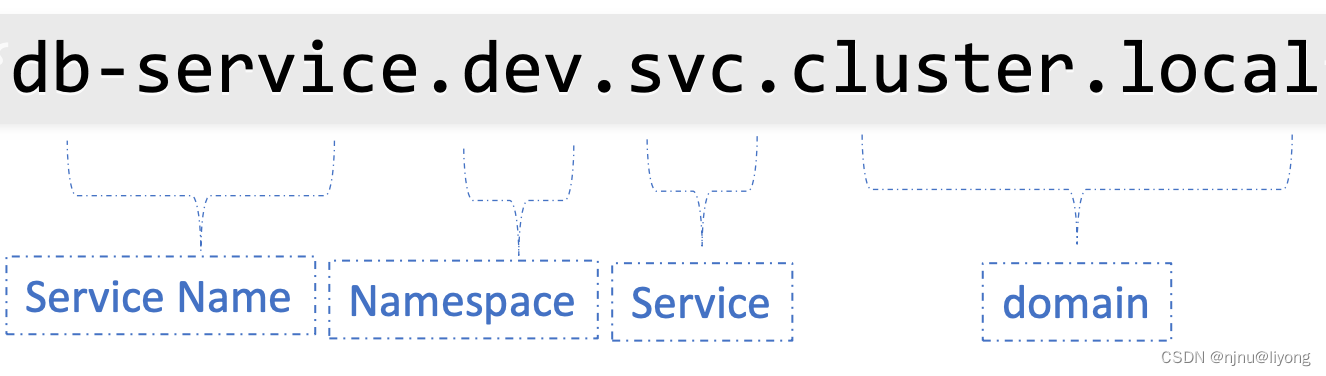
k8s-基础知识(Service,NodePort,CusterIP,NameSpace,资源限制)
Service 它提供了服务程序和外部的各种组件通信的能力: 1 Service 有固定的IP和端口 2 Service 背后是pod在工作 Kubernetes 会给Service分配一个静态 IP 地址,Service自动管理、维护后面动态变化的 Pod 集合,当客户端访问 Serviceÿ…...

【腾讯云】您使用的腾讯云服务存在违规信息,请尽快处理
收到【腾讯云】您使用的腾讯云服务存在违规信息,请尽快处理,如何解决?在腾讯云服务器部署网站提示网站有违规信息如何处理?腾讯云百科txybk告诉各位站长,在腾讯网址安全中心申诉,申诉通过后截图上传给腾讯云…...
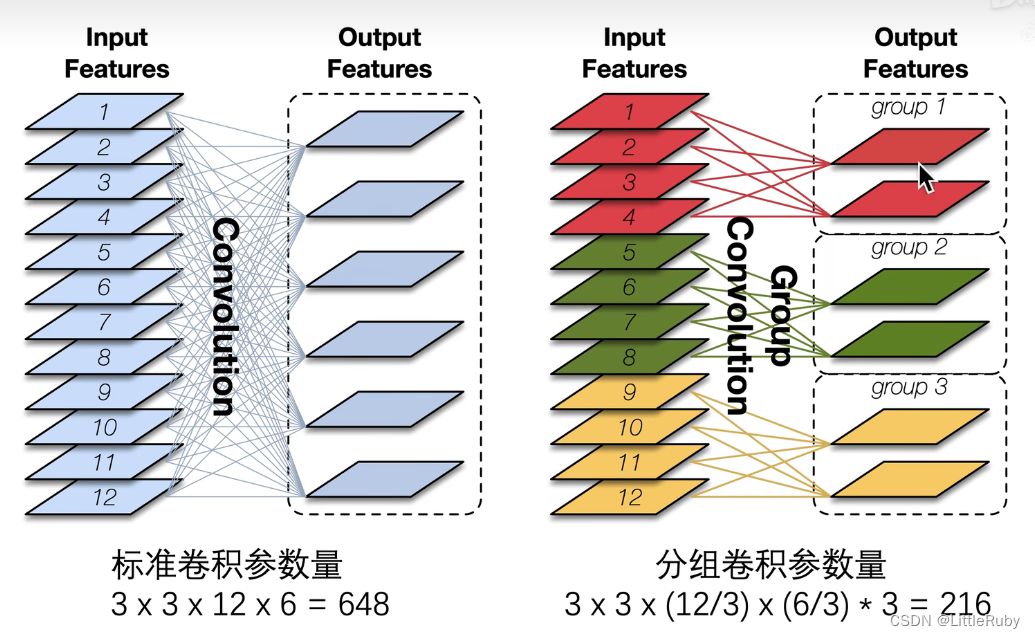
深度学习 Day27——J6ResNeXt-50实战解析
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 | 接辅导、项目定制🚀 文章来源:K同学的学习圈子 文章目录 前言1 我的环境2 pytorch实现DenseNet算法2.1 前期准备2.1.1 引入库2.1.2 设…...
 C++题解(数学+递归+快速幂))
【力扣 50】Pow(x, n) C++题解(数学+递归+快速幂)
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。 示例 1: 输入:x 2.00000, n 10 输出:1024.00000 示例 2: 输入:x 2.10000, n 3 输出:9.26100 …...

速盾:服务器接入CDN后上传图片失败的解决方案
本文将探讨当服务器接入CDN后,上传图片失败的常见原因,并提供解决方案以解决这些问题。同时,我们还将附上一些相关的问题和解答,让读者更好地理解和应对这些挑战。 随着互联网的持续发展,网站的性能和速度对于用户体验…...
LabVIEW高级CAN通信系统
LabVIEW高级CAN通信系统 在现代卫星通信和数据处理领域,精确的数据管理和控制系统是至关重要的。设计了一个基于LabVIEW的CAN通信系统,它结合了FPGA技术和LabVIEW软件,主要应用于模拟卫星平台的数据交换。这个系统的设计不仅充分体现了FPGA在…...
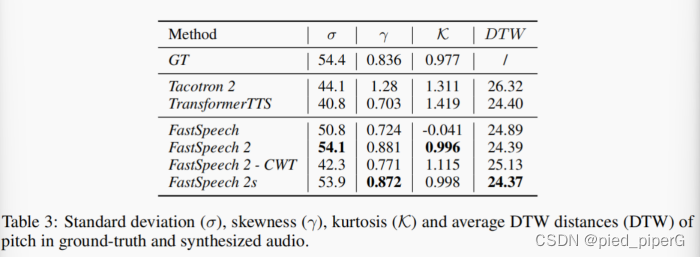
FastSpeech2——TTS论文阅读
笔记地址:https://flowus.cn/share/1683b50b-1469-4d57-bef0-7631d39ac8f0 【FlowUs 息流】FastSpeech2 论文地址:lFastSpeech 2: Fast and High-Quality End-to-End Text to Speechhttps://arxiv.org/abs/2006.04558 Abstract: tacotron→…...
如何才能拥有比特币 - 01 ?
如何才能拥有BTC 在拥有 BTC 之前我们要先搞明白 BTC到底保存在哪里?我的钱是存在银行卡里的,那我的BTC是存在哪里的呢? BTC到底在哪里? 一句话概括,BTC是存储在BTC地址中,而且地址是公开的,…...

Unity | 渡鸦避难所-8 | URP 中利用 Shader 实现角色受击闪白动画
1. 效果预览 当角色受到攻击时,为了增加游戏的视觉效果和反馈,可以添加粒子等动画,也可以使用 Shader 实现受击闪白动画:受到攻击时变为白色,逐渐恢复为正常颜色 本游戏中设定英雄受击时播放粒子效果,怪物…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...

简约商务通用宣传年终总结12套PPT模版分享
IOS风格企业宣传PPT模版,年终工作总结PPT模版,简约精致扁平化商务通用动画PPT模版,素雅商务PPT模版 简约商务通用宣传年终总结12套PPT模版分享:商务通用年终总结类PPT模版https://pan.quark.cn/s/ece1e252d7df...
