图论(蓝桥杯 C++ 题目 代码 注解)
目录
迪杰斯特拉模板(用来求一个点出发到其它点的最短距离):
克鲁斯卡尔模板(用来求最小生成树):
题目一(蓝桥王国):
题目二(随机数据下的最短路径):
题目三(出差):
题目四(聪明的猴子):
题目六(机房):
迪杰斯特拉模板(用来求一个点出发到其它点的最短距离):
#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const ll N = 3e5 + 10, M = 1e6 + 10, inf = 1e14;
struct node
{ll v, w;bool operator <(const node& y) const//重载一个<,用于优先队列排序{return w > y.w;//小到大}
};
int n, m;
priority_queue<node>q;
vector<node> e[N];
ll dis[N], vis[N];
void Dij()
{dis[1] = 0;//从1号点出发,表示从1到1距离为0q.push({ 1,dis[1] });//1号点以及到1的距离入队while (q.size()){int u = q.top().v;//取最小边相连的点出队q.pop();if (vis[u])//访问过则跳过continue;vis[u] = 1;//没访问赋为访问for (auto i : e[u])//遍历以u为出发点的边{int v = i.v, w = i.w;//取其相连的点及权值if (dis[v] > dis[u] + w)//经过u点到v点的权值小于之前的权值则更新{dis[v] = dis[u] + w;q.push({ v,dis[v] });//v点以及到v的距离}}}}
int main()
{cin >> n >> m;fill(dis+1, dis+1+n, inf);//赋值一个无穷大,表示没有连接for (int i = 1; i <= m; i++){int x, y, w;cin >> x >> y >> w;e[x].push_back({ y,w });//存入以x出发到y,权值为w}Dij();
}克鲁斯卡尔模板(用来求最小生成树):
#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 1e3+20;
int m, n;
int h[N],f[N],x[N],y[N];
struct edge
{int v1, v2;double w;
};
vector<edge> e;
int find(int k)//查找
{if (f[k] == k)return k;return f[k] = find(f[k]);
}
void merge(int x, int y)//合并
{x=find(x),y=find(y);if (x!= y)f[x] = f[y];
}
bool cmp(edge a, edge b)
{return a.w < b.w;
}
int main()
{cin >> n;for (int j = 1; j <= n; j++){cin >> x[j] >> y[j]>> h[j];f[j] = j;//初始化并查集根}cin>>m;for (int j = 1; j <= m; j++)//添加边{int v1,v2,w;cin>>v1>>v2>>w;e.push_back({ v1, v2, w });}sort(e.begin(), e.end(), cmp);//边从小到大排序int cnt=0;for (int i = 0; i < e.size(); i++){if (find(e[i].v1) != find(e[i].v2))//不属于一个集合{merge(e[i].v1, e[i].v2);//合并}if (cnt == n-1)//n个点只需要n-1条边,选取n-1条边后,跳出循环break;}
}题目一(蓝桥王国):

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const ll N = 3e5 + 10, M = 1e6 + 10, inf = 1e14;
struct node
{ll v, w;bool operator <(const node& y) const//重载一个<,用于优先队列排序{return w > y.w;//小到大}
};
int n, m;
priority_queue<node>q;
vector<node> e[N];
ll dis[N], vis[N];
void Dij()
{dis[1] = 0;//从1号点出发,表示从1到1距离为0q.push({ 1,dis[1] });//1号点以及到1的距离入队while (q.size()){int u = q.top().v;//取最小边相连的点出队q.pop();if (vis[u])//访问过则跳过continue;vis[u] = 1;//没访问赋为访问for (auto i : e[u])//遍历以u为出发点的边{int v = i.v, w = i.w;//取其相连的点及权值if (dis[v] > dis[u] + w)//经过u点到v点的权值小于之前的权值则更新{dis[v] = dis[u] + w;q.push({ v,dis[v] });//v点以及到v的距离}}}}
int main()
{cin >> n >> m;fill(dis+1, dis+1+n, inf);//赋值一个无穷大,表示没有连接for (int i = 1; i <= m; i++){int x, y, w;cin >> x >> y >> w;e[x].push_back({ y,w });//存入以x出发到y,权值为w}Dij();for (int i = 1; i <= n; i++){if (dis[i] >= inf)//无法到达cout << -1 << " ";elsecout << dis[i] << " ";}
}题目二(随机数据下的最短路径):

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const ll N = 3e5 + 10, M = 1e6 + 10, inf = 1e14;
struct node
{ll v, w;bool operator <(const node& y) const//重载一个<,用于优先队列排序{return w > y.w;//小到大}
};
int n, m, t;
priority_queue<node>q;
vector<node> e[N];
ll dis[N], vis[N];
void Dij(int t)
{dis[t] = 0;//从t号点出发,表示从t到t距离为0q.push({ t,dis[t] });//t号点以及到t的距离入队while (q.size()){int u = q.top().v;//取最小边相连的点出队q.pop();if (vis[u])//访问过则跳过continue;vis[u] = 1;//没访问赋为访问for (auto i : e[u])//遍历以u为出发点的边{int v = i.v, w = i.w;//取其相连的点及权值if (dis[v] > dis[u] + w)//经过u点到v点的权值小于之前的权值则更新{dis[v] = dis[u] + w;q.push({ v,dis[v] });//v点以及到v的距离}}}}
int main()
{cin >> n >> m>> t;fill(dis+1, dis+1+n, inf);//赋值一个无穷大,表示没有连接for (int i = 1; i <= m; i++){int x, y, w;cin >> x >> y >> w;e[x].push_back({ y,w });//存入以x出发到y,权值为w}Dij(t);//从t点出发for (int i = 1; i <= n; i++){if (dis[i] == inf)//无法到达cout << -1 << " ";elsecout << dis[i] << " ";}
}题目三(出差):

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const ll N = 3e5 + 10, M = 1e6 + 10, inf = 1e14;
struct node
{int v, w;bool operator <(const node& y) const//重载一个<,用于优先队列排序{return w > y.w;//小到大}
};
int n, m;
priority_queue<node>q;
vector<node> e[N];
int dis[N], vis[N], time0[N];
void Dij()
{dis[1] = 0;//从1号点出发,表示从1到1距离为0q.push({ 1,dis[1] });//1号点以及到1的距离入队while (q.size()){int u = q.top().v;//取最小边相连的点出队q.pop();if (vis[u])//访问过则跳过continue;vis[u] = 1;//没访问赋为访问for (auto i : e[u])//遍历以u为出发点的边{int v = i.v, w = i.w;//取其相连的点及权值if (dis[v] > dis[u] + w)//经过u点到v点的权值小于之前的权值则更新{dis[v] = dis[u] + w;q.push({ v,dis[v] });//v点以及到v的距离}}}
}
int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)cin >> time0[i];fill(dis + 1, dis + 1 + n, inf);//赋值一个无穷大,表示没有连接for (int i = 1; i <= m; i++){int x, y, w;cin >> x >> y >> w;e[x].push_back({ y,w + time0[y]});//存入以x出发到y,权值为w+隔离时间e[y].push_back({ x,w + time0[x] });//存入以y出发到y,权值为w+隔离时间}Dij();cout << dis[n] - time0[n];//要减掉最后终点的隔离时间
}题目四(聪明的猴子):


#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 1e3+20;
int m, n;
int a[N],f[N],x[N],y[N];
struct edge
{int v1, v2;double w;
};
vector<edge> e;
int find(int k)//查找
{if (f[k] == k)return k;return f[k] = find(f[k]);
}
void merge(int x, int y)//合并
{x=find(x),y=find(y);if (x!= y)f[x] = f[y];
}
bool cmp(edge a, edge b)
{return a.w < b.w;
}
int main()
{cin >> m;for (int i = 1; i <= m; i++)cin >> a[i];cin >> n;for (int j = 1; j <= n; j++){cin >> x[j] >> y[j];f[j] = j;//初始化并查集根}for(int i=1;i<=n;i++)for (int j = i + 1; j <= n; j++)//添加边{double w = sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));e.push_back({ i, j, w });}sort(e.begin(), e.end(), cmp);//边从小到大排序double maxw = 0.0;//记录最小生成树中最大边int cnt = 0;for (int i = 0; i < e.size(); i++){if (find(e[i].v1) != find(e[i].v2))//不属于一个集合{merge(e[i].v1, e[i].v2);//合并cnt++;maxw = max(maxw, e[i].w);//更新最小生成树中最大边}if (cnt == n-1)//n个点只需要n-1条边,选取n-1条边后,跳出循环break;}int ans = 0;for (int i = 1; i <= m; i++){if (a[i] >= maxw)//有几只猴子大于最小生成树中最大边ans++;}cout << ans;
}题目五(通电):

#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 1e3+20;
int m, n;
int h[N],f[N],x[N],y[N];
struct edge
{int v1, v2;double w;
};
vector<edge> e;
int find(int k)//查找
{if (f[k] == k)return k;return f[k] = find(f[k]);
}
void merge(int x, int y)//合并
{x=find(x),y=find(y);if (x!= y)f[x] = f[y];
}
bool cmp(edge a, edge b)
{return a.w < b.w;
}
int main()
{cin >> n;for (int j = 1; j <= n; j++){cin >> x[j] >> y[j]>> h[j];f[j] = j;//初始化并查集根}for(int i=1;i<=n;i++)for (int j = i + 1; j <= n; j++)//添加边{double w = sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]))+(h[i]-h[j])*(h[i]-h[j]);e.push_back({ i, j, w });}sort(e.begin(), e.end(), cmp);//边从小到大排序double maxw = 0.0;//记录最小生成树中最大边double ans=0;int cnt=0;for (int i = 0; i < e.size(); i++){if (find(e[i].v1) != find(e[i].v2))//不属于一个集合{merge(e[i].v1, e[i].v2);//合并ans+=e[i].w;//求和maxw = max(maxw, e[i].w);//更新最小生成树中最大边}if (cnt == n-1)//n个点只需要n-1条边,选取n-1条边后,跳出循环break;}printf("%.2lf",ans);
}题目六(机房):


#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const ll N = 3e5 + 10, M = 1e6 + 10;
struct node
{ll v, w;bool operator <(const node& y) const//重载一个<,用于优先队列排序{return w > y.w;//小到大}
};
int n, m;
priority_queue<node>q;
vector<node> e[N];
vector<node> temp;
ll dis[N], vis[N], cnt[N];
ll Dij(int u, int end)
{memset(vis, 0, sizeof(vis));memset(dis, 0x3f3f, sizeof(dis));dis[u] = 0;//从u号点出发,表示从u到u距离为0q.push({ u,dis[u] });//u号点以及到u的距离入队while (q.size()){int u = q.top().v;//取最小边相连的点出队q.pop();if (vis[u])//访问过则跳过continue;vis[u] = 1;//没访问赋为访问for (auto i : e[u])//遍历以u为出发点的边{int v = i.v, w = i.w;//取其相连的点及权值if (dis[v] > dis[u] + w)//经过u点到v点的权值小于之前的权值则更新{dis[v] = dis[u] + w;q.push({ v,dis[v] });//v点以及到v的距离}}}return dis[end]+cnt[end];//还需要加上自身延迟
}
int main()
{cin >> n >> m;for (int i = 1; i <= n - 1; i++){int x, y;cin >> x >> y;cnt[x]++, cnt[y]++;temp.push_back({ x,y });//临时存两个顶点}for (int i = 0; i < n - 1; i++)//根据度构造边{int u = temp[i].v, v = temp[i].w;e[u].push_back({ v,cnt[u] });//u->v的边,权值为u的度e[v].push_back({ u,cnt[v] });}while (m--)//m次查询{int u, v;cin >> u >> v;if (u == v)cout << cnt[u] << endl;else{ll ans = Dij(u, v);cout << ans << endl;}}
}相关文章:

图论(蓝桥杯 C++ 题目 代码 注解)
目录 迪杰斯特拉模板(用来求一个点出发到其它点的最短距离): 克鲁斯卡尔模板(用来求最小生成树): 题目一(蓝桥王国): 题目二(随机数据下的最短路径&#…...

矩阵起源新一年喜报连连!
新春伊始 矩阵起源向大家分享 一连串好消息 首先,公司创始人兼CEO王龙先生获评“2023深圳创新突出贡献人物“。这一荣誉是对其在推动数据库行业技术创新和产品开发方面所做出的卓越贡献的认可。他的领导力和创新精神不仅引领我司取得了显著的成就,也为…...
牛客——紫魔法师(并查集)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 “サーヴァント、キャスター、Medea。”--紫魔法师 给出一棵仙人掌(每条边最多被包含于一个环,无自环,无重边,保证连通),要求用最少的…...
最新WooCommerce教程指南-如何搭建B2C外贸独立站
WooCommerce是全球最受欢迎的开源电子商务平台之一。它基于WordPress建站,只需一键安装即可使用。该平台提供了丰富的功能,包括产品发布、库存管理、支付网关和运输发货等,可以帮助搭建各种类型的电子商务网站。相比其他竞争对手,…...
一文教会你SpringBoot是如何启动的
SpringBoot启动流程分析 流程图 源码剖析 运行Application.run()方法 我们在创建好一个 SpringBoot 程序之后,肯定会包含一个类:xxxApplication,我们也是通过这个类来启动我们的程序的(梦开始的地方),而…...
车载测试面试:各大车企面试题汇总
本博主可协助大家成功进军车载测试行业 TBOX 深圳 涉及过T-BOX测试吗Ota升级涉及的台架环境是什么样的?上车实测之前有没有一个仿真环境台架环境都什么零部件T-BOX了解多少Linux和shell有接触吗 单片机uds诊断是在实车上座的吗 uds在实车上插的那口 诊断仪器是哪…...

Qt散文一
Qt的事件分为普通事件和系统事件,普通事件比如用户按下键盘,系统事件比如定时器事件。事件循环的开始是从main函数的QApplication,然后调用exec()开始的,在执行exec()函数之后,程序将进入事件循环来监听应用程序的事件…...
MySQL学习Day32——数据库备份与恢复
在任何数据库环境中,总会有不确定的意外情况发生,比如例外的停电、计算机系统中的各种软硬件故障、人为破坏、管理员误操作等是不可避免的,这些情况可能会导致数据的丢失、 服务器瘫痪等严重的后果。存在多个服务器时,会出现主从服…...

阅读基础知识
一 网络 1. 三次握手四次挥手 三次握手:为了建立长链接进行交互即建立一个会话,使用 http/https 协议 ① 客户端产生初始化序列号 Seqx ,向服务端发送建立连接的请求报文,将 SYN1 同步序列号; ② 服务端接收建立连接…...

【NestJS 编程艺术】1. NestJS设计模式深度解析:构建高效、可维护的服务端应用
在当今快速发展的软件开发领域,Node.js凭借其轻量级和高性能的特点,已经成为了构建服务端应用的首选技术之一。然而,随着应用规模的扩大,传统的Node.js框架如Express和Koa可能在架构设计和代码组织上显得力不从心。这时࿰…...
的参数5:Qt::DirectConnection、Qt::QueuedConnection区别)
QT中connect()的参数5:Qt::DirectConnection、Qt::QueuedConnection区别
原文链接:https://blog.csdn.net/Dasis/article/details/120916993 connect用于连接QT的信号和槽,在qt编程过程中不可或缺。它其实有第5个参数,只是一般使用默认值,在满足某些特殊需求的时候可能需要手动设置。 Qt::AutoConnect…...
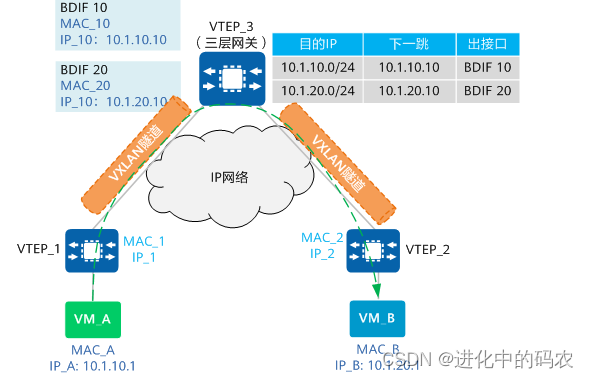
VXLAN学习笔记
声明:该博客内容大部分参考参考链接整理 什么是VXLAN? VXLAN(Virtual Extensible LAN)即虚拟扩展局域网,是大二层网络中广泛使用的网络虚拟化技术。在源网络设备与目的网络设备之间建立一条逻辑VXLAN隧道,采用MAC in UDP的封装方…...
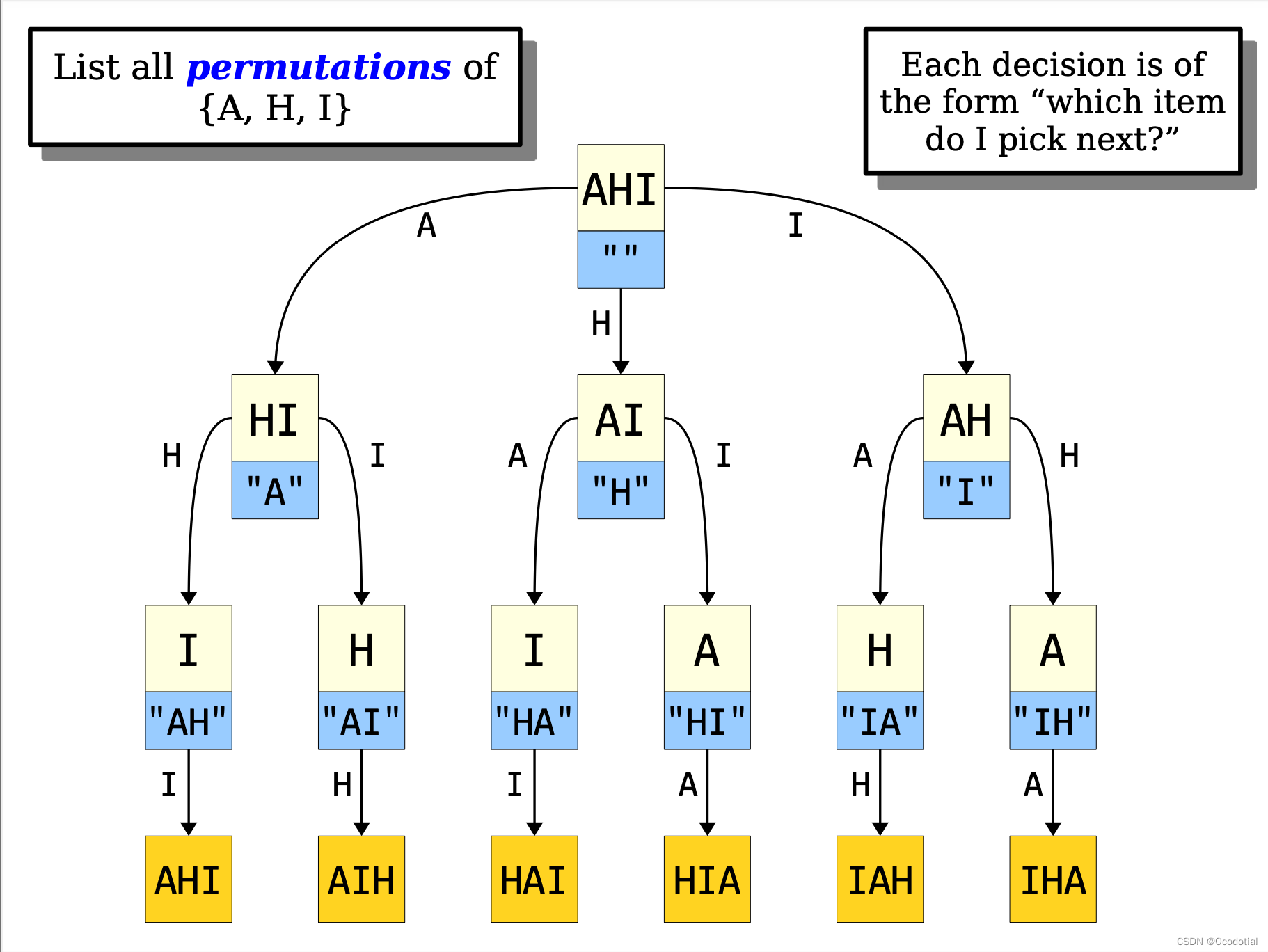
全排列的不同写法(茴字的不同写法)及对应的时间开销
资源课件: CS106B-recursion-pptstanford library-timer.hstanford library-set.h 不同的方法 1------ Set<string> permutations1Rec(string remaining) {Set<string> res;if(remaining.size() 0) {res "";}else {for(int i 0; i <…...

权衡后台数据库设计中是否使用外键
目录 引言 外键简介 对比 真实后台项目中的权衡 结论 引言 在大学学习数据库课程时,我们会早早的接触到外键这一概念,同时我相信大部分人在懂了外键的概念后都会觉得外键很重要,在涉及多表一定要用,但后来在我接触到真实项目…...
ChatGPT提示词方法的原理
关于提示词,我之前的一些文章可以参考: 【AIGC】AI作图最全提示词prompt集合(收藏级)https://giszz.blog.csdn.net/article/details/134815245?ydrefereraHR0cHM6Ly9tcC5jc2RuLm5ldC9tcF9ibG9nL21hbmFnZS9hcnRpY2xlP3NwbT0xMDExL…...

计算机网络 谢希仁(001-1)
计算机网络-方老师 总时长 24:45:00 共50个视频,6个模块 此文章包含1.1到1.4的内容 简介 1.1计算机网络的作用 三网融合(三网合一) 模拟信号就是连续信号 数字信号是离散信号 1.2互联网概述 以前2兆带宽就要98 现在几百兆带宽也就几百块 …...

Windows,MacOS,Linux下载python并配置环境图文讲解
Windows 打开python官网 点击download 点击黄色按钮 另存为 打开文件 全选 配置安装路径 安装中 关闭路径长度限制 完成 验证 同时按住winr(win就是空格键左边的东西) 输入cmd 键入python,如果出现版本(红框)即安装成功 MacOS 同理打开python官网 点击最新版本 拖…...
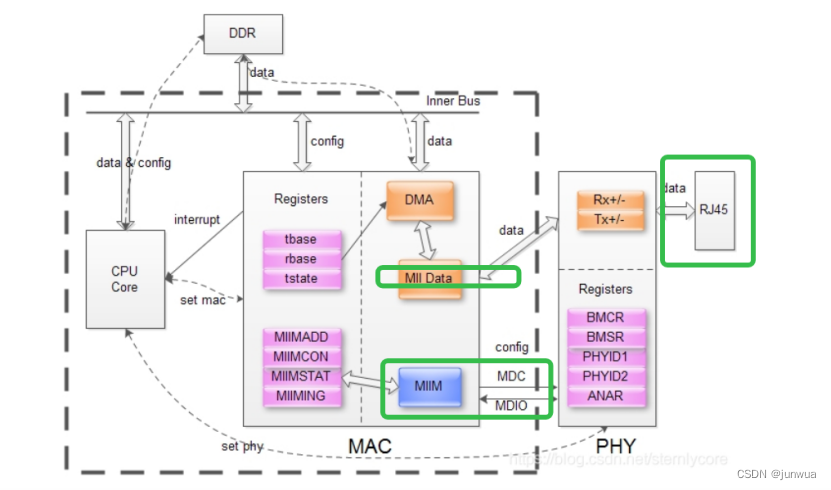
汽车网络基础知识 要点
在以太网开发中,常常会听到一些专业名词,例如PHY,MAC,MII,switch,下面是解释 PHY PHY 是物理接口收发器,它实现物理层。包括 MII/GMII (介质独立接口) 子层、PCS (物理编码子层) 、PMA (物理介…...
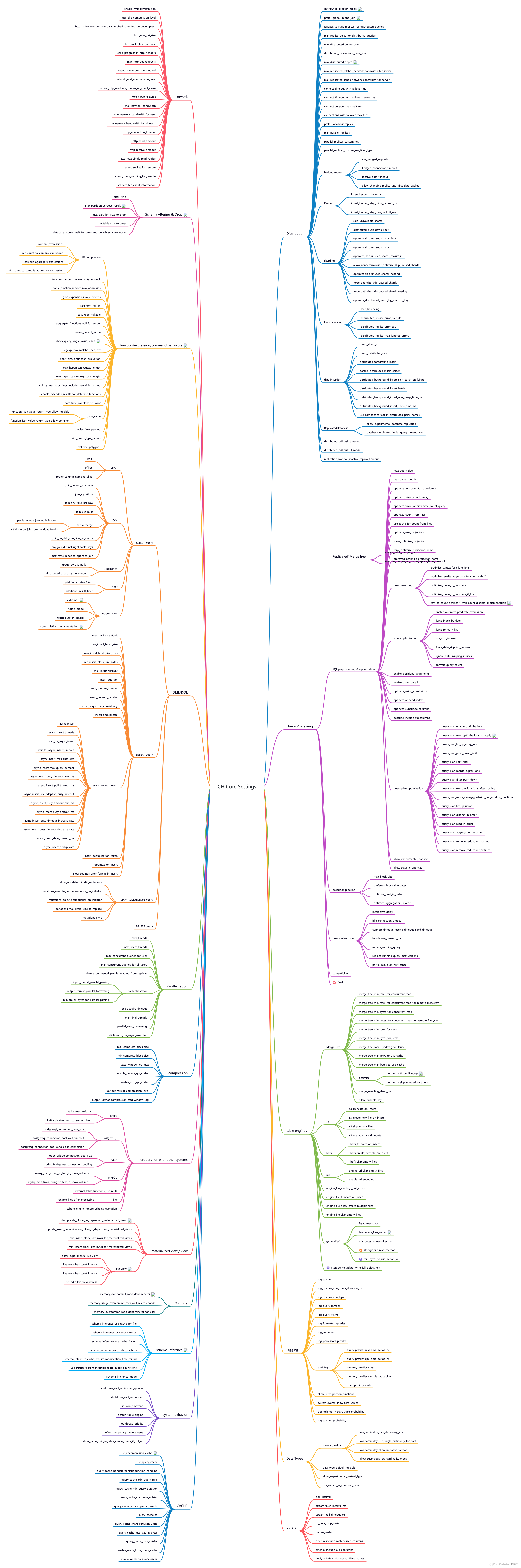
ClickHouse中的设置的分类
ClickHouse中的各种设置 ClickHouse中的设置有几百个,下面对这些设置做了一个简单的分类。...

香港空间服务器带宽和流量限制:原因和解决方法
香港空间服务器,也被称作香港虚拟服务器。一般情况下,香港空间服务器所提供的流量或者带宽,是足以满足99%的普通中小网站用户使用的,但也不排除,网站访问量大,租香港空间不能够满足要求的情况。 在本…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
