Llama改进之——SwiGLU激活函数
引言
今天介绍LLAMA模型引入的关于激活函数的改进——SwiGLU1,该激活函数取得了不错的效果,得到了广泛地应用。
SwiGLU是GLU的一种变体,其中包含了GLU和Swish激活函数。
GLU
GLU(Gated Linear Units,门控线性单元)2引入了两个不同的线性层,其中一个首先经过sigmoid函数,其结果将和另一个线性层的输出进行逐元素相乘作为最终的输出:
GLU ( x , W , V , b , c ) = σ ( x W + b ) ⊗ ( x V + c ) (1) \text{GLU}(x,W,V,b,c) = \sigma(xW+b) \otimes (xV+c) \tag 1 GLU(x,W,V,b,c)=σ(xW+b)⊗(xV+c)(1)
这里 W , V W,V W,V以及 b , c b,c b,c分别是这两个线性层的参数; σ ( x W + b ) \sigma(xW+b) σ(xW+b)作为门控,控制 x V + c xV+c xV+c的输出。
这里使用 σ \sigma σ作为激活函数,修改改激活函数得到的变体通常能带来更好的性能表现,比如SwiGLU修改激活函数为Swish。我们来看下Swish激活函数。
Swish
Swish3激活函数的形式为:
Swish β ( x ) = x σ ( β x ) (2) \text{Swish}_\beta(x) = x \sigma(\beta x) \tag 2 Swishβ(x)=xσ(βx)(2)
其中 σ ( x ) \sigma(x) σ(x)是Sigmoid函数; β \beta β是一个可学习的参数。
可以通过下面的代码画出Swish激活函数在不同参数 β \beta β下的图像:
import numpy as np
import matplotlib.pyplot as pltdef swish(x, beta):return x / (1 + np.exp(-beta*x))x = np.linspace(-10, 10, 100)
betas = [0.1, 1.0, 10.0]plt.figure(figsize=(10, 6))for beta in betas:y = swish(x, beta)plt.plot(x, y, label=f'beta={beta}')plt.legend()
plt.title('Swish Activation Function')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.show()
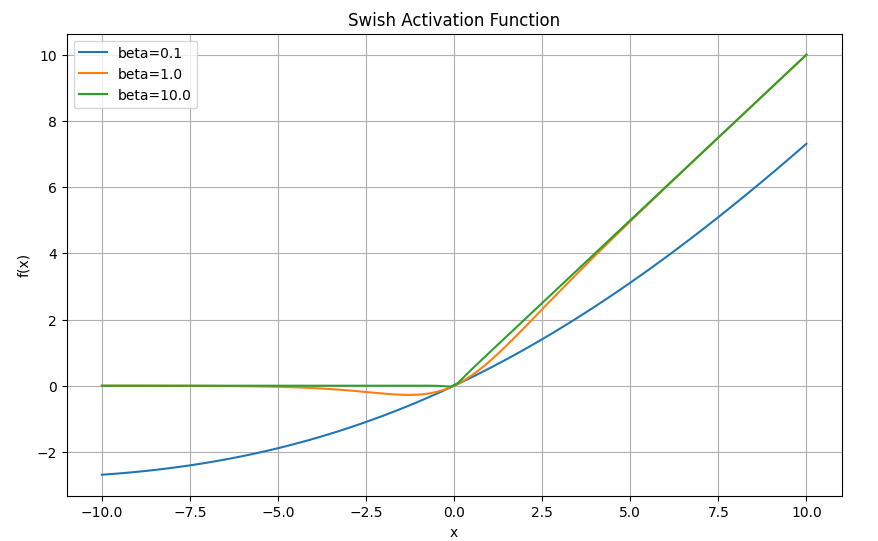
可以看到3,当 β \beta β趋近于 0 0 0时,Swish函数趋近于线性函数 y = x 2 y=x^2 y=x2;当 β \beta β趋近于无穷大时,Swish函数趋近于ReLU函数;当 β \beta β取值为 1 1 1时,Swish函数是光滑且非单调的,等价于参考4中介绍的SiLU。
Swish与ReLU之间最显著的区别是当 x < 0 x < 0 x<0时Swish的非单调“凸起”3。
SwiGLU
如前文所述,将公式(1)中GLU的激活函数改为Swish即变成了所谓的SwiGLU激活函数1:
SwiGLU ( x , W , V ) = Swish β ( x W ) ⊗ ( x V ) (3) \text{SwiGLU}(x,W,V) = \text{Swish}_\beta(xW) \otimes (xV) \tag{3} SwiGLU(x,W,V)=Swishβ(xW)⊗(xV)(3)
这里省略了偏置项。
代码实现
参考LLaMA,全连接层使用带有SwiGLU激活函数的FFN(Position-wise Feed-Forward Network)的公式如下1:
FFN SwiGLU ( x , W , V , W 2 ) = ( Swish 1 ( x W ) ⊗ x V ) W 2 (4) \text{FFN}_{\text{SwiGLU}}(\pmb x,W,V,W_2) = (\text{Swish}_1(\pmb xW) \otimes \pmb xV)W_2 \tag 4 FFNSwiGLU(x,W,V,W2)=(Swish1(xW)⊗xV)W2(4)
这里的Swish函数可以被SiLU函数替代:
SiLU ( x ) = x σ ( x ) \text{SiLU}(\pmb x) = \pmb x \sigma(\pmb x) SiLU(x)=xσ(x)
即:
FFN SwiGLU ( x , W , V , W 2 ) = ( SiLU ( x W ) ⊗ x V ) W 2 (5) \text{FFN}_{\text{SwiGLU}}(\pmb x,W,V,W_2) = (\text{SiLU}(\pmb xW) \otimes \pmb xV)W_2 \tag 5 FFNSwiGLU(x,W,V,W2)=(SiLU(xW)⊗xV)W2(5)
import torch
from torch import nn
import torch.nn.functional as Fclass FeedForward(nn.Module):def __init__(self, hidden_size: int, intermediate_size: int) -> None:super().__init__()self.w1 = nn.Linear(hidden_size, intermediate_size, bias=False)self.w2 = nn.Linear(intermediate_size, hidden_size, bias=False)self.w3 = nn.Linear(hidden_size, intermediate_size, bias=False)def forward(self, x: torch.Tensor) -> torch.Tensor:# x: (batch_size, seq_len, hidden_size)# w1(x) -> (batch_size, seq_len, intermediate_size)# w1(x) -> (batch_size, seq_len, intermediate_size)# w2(*) -> (batch_size, seq_len, hidden_size)return self.w2(F.silu(self.w1(x)) * self.w3(x))这里w1,w2,w3分别对应公式(5)中的 W , W 2 , V W,W_2,V W,W2,V。
注意维度,其中w1,w3将x转换到维度intermediate_size,然后w2转换回hidden_size。
参考
[论文翻译]GLU Variants Improve Transformer ↩︎ ↩︎ ↩︎
[论文笔记]Language Modeling with Gated Convolutional Networks ↩︎
[论文笔记]SEARCHING FOR ACTIVATION FUNCTIONS ↩︎ ↩︎ ↩︎
[论文笔记]GAUSSIAN ERROR LINEAR UNITS (GELUS) ↩︎
相关文章:

Llama改进之——SwiGLU激活函数
引言 今天介绍LLAMA模型引入的关于激活函数的改进——SwiGLU1,该激活函数取得了不错的效果,得到了广泛地应用。 SwiGLU是GLU的一种变体,其中包含了GLU和Swish激活函数。 GLU GLU(Gated Linear Units,门控线性单元)2引入了两个不同的线性层…...
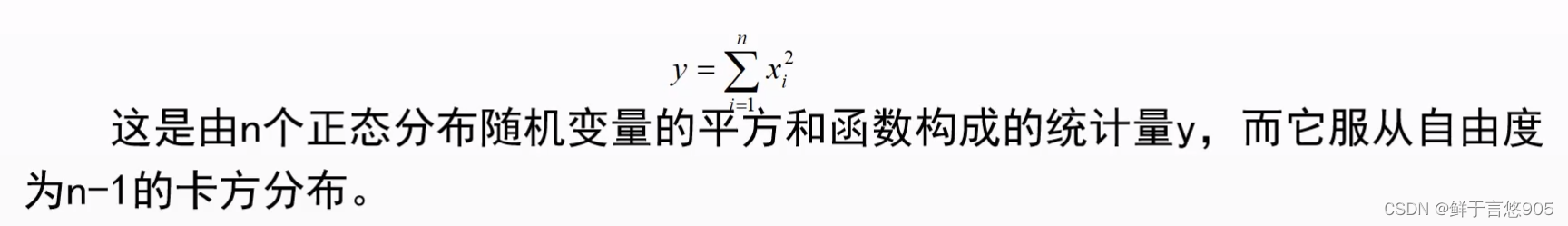
在数据分析中所需要运用到的概率论知识
数据分析 前言一、总体二、样本三、统计抽样抽取的基本准则 四、随机抽样抽签法随机数法 五、分层抽样六、整群抽样七、系统抽样八、统计参数常用的分布函数参数 九、样本统计量十、样本均值和样本方差十一、描述样本集中位置的统计量样本均值样本中位数样本众数 十二、描述样本…...

韩顺平0基础学Java——第6天
p87-p109 运算符(第四章) 四种进制 二进制用0b或0B开头 十进制略 八进制用0开头 十六进制0x或0X开头,其中的A—F不区分大小写 10转2:将这个数不断除以2,直到商为0,然后把每步得到的余数倒过来&#…...

react18子组件设置接收默认值和值类型验证
父组件传值 import ChildCom from ./components/ChildCom export default function Person {return(<div><ChildCom name"alan-ben" age{18} score{[98, 97, 100]} /></div>) } 子组件接收并验证类型 import React from react import PropTypes…...
)
Java 高级面试问题及答案(二)
Java高级面试问题及答案 1. 在Java中,什么是强引用、软引用、弱引用和虚引用,它们有什么区别? 答案: 在Java中,引用类型决定了对象的生命周期,主要有以下四种: 强引用:最常见的引…...
数据统计:词频统计、词表生成、排序及计数、词云图生成
文章目录 📚输入及输出📚代码实现 📚输入及输出 输入:读取一个input.txt,其中包含单词及其对应的TED打卡号。 输出 output.txt:包含按频率降序排列的每个单词及其计数(这里直接用于后续的词云…...
W801学习笔记二十四:NES模拟器游戏
之前已经实现了NES模拟器玩游戏。W801学习笔记九:HLK-W801制作学习机/NES游戏机(模拟器) 现在要在新版本掌机中移植过来。 1、把NES文件都拷贝到SD卡中。 这回不会受内存大小限制了。我这里拷贝了4个,还可以拷贝更多。 2、应用初始化中,加载…...

ECMAScript 6简介
ECMAScript 6简介 发布日期目标ECMAScript 和 JavaScript 的关系ES6 与 ECMAScript 2015 的关系 ESx标准 命名规则 ECMAScript 的历史 1. ECMAScript 6简介 1.1. 发布日期 ECMAScript 6.0(以下简称 ES6)是 JavaScript 语言的下一代标准,已…...

第1个数据库:编号,文本,时间,
写一个数据库 编号 文本 时间1 第一个文本 有100万条数据 -- 创建一个名为texts的表格来存储数据 CREATE TABLE texts ( id INTEGER PRIMARY KEY, text TEXT, time TIMESTAMP DEFAULT CURRENT_TIMESTAMP);-- 插入数据INSERT INTO texts (text) VALUES (第一个文…...

线性数据结构-手写链表-LinkList
为什么需要手写实现数据结构? 其实技术的本身就是基础的积累和搭建的过程,基础扎实 地基平稳 万丈高楼才会久战不衰,做技术能一通百,百通千就不怕有再难得技术了。 一:链表的分类 主要有单向,双向和循环链表…...

快手客户端一二面+美团前端一面+腾讯企业微信开发客户端一面
快手一面结志 1、自我介绍 2、对称加密非对称加密 3、TCP/UDP 4、在学校有什么课程是强项,说了过去几次面试中面到的C的语言基础知识 5、问C、Java中兴趣在哪里 6、问到项目,自己做的还是跟着学校老师做的,同样问到兴趣在哪里 7、LRU …...
探索数据结构
什么是数据结构 数据结构是由:“数据”与“结构”两部分组成 数据与结构 数据:如我们所看见的广告、图片、视频等,常见的数值,教务系统里的(姓名、性别、学号、学历等等); 结构:当…...

VMware虚拟机中ubuntu使用记录(6)—— 如何标定单目相机的内参(张正友标定法)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、张正友相机标定法1. 工具的准备2. 标定的步骤(1) 启动相机(2) 启动标定程序(3) 标定过程的操作(5)可能的报错 3. 标定文件内容解析 前言 张正友相机标定法…...
每日OJ题_记忆化搜索②_力扣62. 不同路径(三种解法)
目录 力扣62. 不同路径 解析代码1_暴搜递归(超时) 解析代码2_记忆化搜索 解析代码3_动态规划 力扣62. 不同路径 62. 不同路径 难度 中等 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器…...
【微信小程序开发】微信小程序、大前端之flex布局方式详细解析
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...
代码随想录算法训练营第二十天:二叉树成长
代码随想录算法训练营第二十天:二叉树成长 110.平衡二叉树 力扣题目链接(opens new window) 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝…...

Opensbi初始化分析:设备初始化-warmboot
Opensbi初始化分析:设备初始化-warmboot 设备初始化sbi_init函数init_warmboot函数coolboot & warmbootwait_for_coldboot函数domain && scratch(coldboot所特有)console初始化及print相关工作(coldboot所特有)系统调用的相关初始化(coldboot所特有)综上设备…...
)
软考 系统架构设计师系列知识点之软件可靠性基础知识(13)
接前一篇文章:软考 系统架构设计师系列知识点之软件可靠性基础知识(12) 所属章节: 第9章. 软件可靠性基础知识 第3节 软件可靠性管理 为了进一步提高软件可靠性,人们又提出了软件可靠性管理的概念,把软件可…...
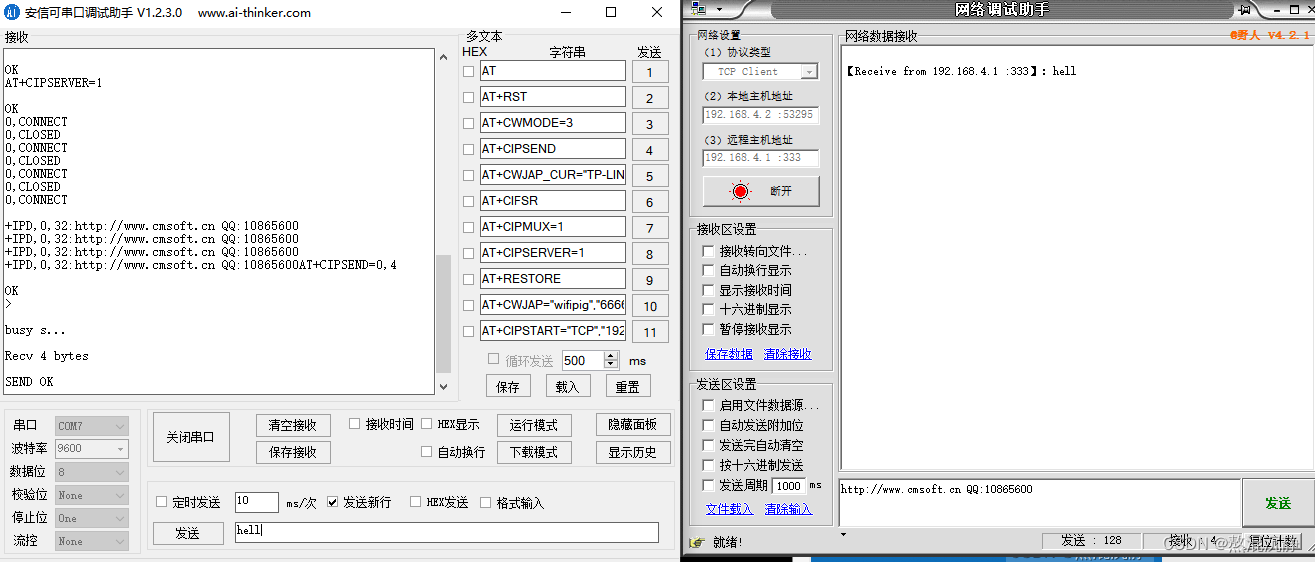
将ESP工作为AP路由模式并当成服务器
将ESP8266模块通过usb转串口接入电脑 ATCWMODE3 //1.配置成双模ATCIPMUX1 //2.使能多链接ATCIPSERVER1 //3.建立TCPServerATCIPSEND0,4 //4.发送4个字节在链接0通道上 >ATCIPCLOSE0 //5.断开连接通过wifi找到安信可的wifi信号并连接 连接后查看自己的ip地址变为192.168.4.…...
Python深度学习基于Tensorflow(6)神经网络基础
文章目录 使用Tensorflow解决XOR问题激活函数正向传播和反向传播解决过拟合权重正则化Dropout正则化批量正则化 BatchNormal权重初始化残差连接 选择优化算法传统梯度更新算法动量算法NAG算法AdaGrad算法RMSProp算法Adam算法如何选择优化算法 使用tf.keras构建神经网络使用Sequ…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
