常见的8种排序(含代码):插入排序、冒泡排序、希尔排序、快速排序、简单选择排序、归并排序、堆排序、基数排序
时间复杂度O(n^2)
1、插入排序 (Insertion Sort)
从第一个元素开始,该元素可以认为已经被排序;取出下一个元素,在已经排序的元素序列中从后向前扫描;如果该元素(已排序)大于新元素,将该元素移到下一位置;重复步骤,直到找到已排序的元素小于或者等于新元素的位置;将新元素插入到该位置后。
void insertionSort(int arr[], int n) { for (int i = 1; i < n; ++i) { int key = arr[i]; int j = i - 1; while (j >= 0 && arr[j] > key) { arr[j + 1] = arr[j]; --j; } arr[j + 1] = key; }
}2、冒泡排序 (Bubble Sort)
重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
void bubbleSort(int arr[], int n) { for (int i = 0; i < n - 1; ++i) { for (int j = 0; j < n - i - 1; ++j) { if (arr[j] > arr[j + 1]) { std::swap(arr[j], arr[j + 1]); } } }
}3、简单选择排序 (Selection Sort)
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
void selectionSort(int arr[], int n) { for (int i = 0; i < n - 1; i++) { int min_idx = i; for (int j = i + 1; j < n; j++) { if (arr[j] < arr[min_idx]) { min_idx = j; } } std::swap(arr[min_idx], arr[i]); }
} 时间复杂度O(nlog2n)
4、希尔排序(Shell Sort)
是插入排序的一种又称“缩小增量排序”,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法的基本思想是:先将整个待排序的记录序列分割成为若干子序列(由相隔某个“增量”的记录组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
(这里只给出增量的简化选择,实际应用中增量序列的选择会更复杂)
void shellSort(int arr[], int n) { int gap = n / 2; while (gap > 0) { for (int i = gap; i < n; ++i) { int temp = arr[i]; int j = i; while (j >= gap && arr[j - gap] > temp) { arr[j] = arr[j - gap]; j -= gap; } arr[j] = temp; } gap /= 2; }
}5、快速排序(Quick Sort)
通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
int partition(int arr[], int low, int high) { int pivot = arr[high]; int i = (low - 1); for (int j = low; j <= high - 1; j++) { if (arr[j] < pivot) { i++; std::swap(arr[i], arr[j]); } } std::swap(arr[i + 1], arr[high]); return (i + 1);
} void quickSort(int arr[], int low, int high) { if (low < high) { int pi = partition(arr, low, high); quickSort(arr, low, pi - 1); quickSort(arr, pi + 1, high); }
}6、堆排序(Heap Sort)
堆排序是利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。堆排序主要要解决两个问题:
1)如何根据给定的序列建初始堆
2)如何在交换掉根结点后,将剩下的结点调整为新的堆(筛选)
void set(int p,int m){//小顶堆int i,j;i=p;j=i*2;while(j<=m){if(j<=m-1&&k[j]>k[j+1])//改为<j++;if(k[j]>=k[i])//改为<=,则为大顶堆break;else{swap(k[i],k[j]);i=j;j=i*2;}}
}void heapSort(){int i,j;for(i=n/2;i>0;i--)//建堆set(i,n);for(i=n;i>1;i--)//排序{swap(k[i],k[1]);set(1,i-1);}
}7、归并排序 (Merge Sort)
归并排序采用分治法的思想,将数组分成两半,分别对它们进行排序,然后将结果合并起来。
1)编写一个辅助函数来合并两个已排序的子数组。
2)编写主归并排序函数,该函数将递归地分解数组,直到子数组只包含一个元素(已排序),然后合并这些子数组,直到整个数组排序完成。
void merge(int arr[], int left[], int leftSize, int right[], int rightSize) { int i = 0, j = 0, k = 0; while (i < leftSize && j < rightSize) { if (left[i] <= right[j]) { arr[k++] = left[i++]; } else { arr[k++] = right[j++]; } } while (i < leftSize) { arr[k++] = left[i++]; } while (j < rightSize) { arr[k++] = right[j++]; }
} void mergeSort(int arr[], int left, int right) { if (left < right) { int mid = left + (right - left) / 2; int leftSize = mid - left + 1; int rightSize = right - mid; int leftArr[leftSize], rightArr[rightSize]; // 拷贝数据到临时数组 for (int i = 0; i < leftSize; i++) { leftArr[i] = arr[left + i]; } for (int j = 0; j < rightSize; j++) { rightArr[j] = arr[mid + 1 + j]; } // 递归地对子数组进行排序 mergeSort(leftArr, 0, leftSize - 1); mergeSort(rightArr, 0, rightSize - 1); // 合并两个已排序的子数组 merge(arr, leftArr, leftSize, rightArr, rightSize); }
}
时间复杂度O(d(n+rd))
8、基数排序(Radix Sort)
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。为了适用于负数和非整数,这里给出一个简化的版本,仅适用于非负整数,并且假设所有整数的位数相同(或可以通过填充前导零来使它们具有相同的位数)。
#include <vector>
#include <algorithm> void countingSort(std::vector<int>& arr, int exp) { std::vector<int> output(arr.size()); std::vector<int> count(10, 0); // 存储每个桶中的元素数量 for (int i = 0; i < arr.size(); i++) count[(arr[i] / exp) % 10]++; // 更改count[i],使其包含每个数字小于或等于i的数量 for (int i = 1; i < 10; i++) count[i] += count[i - 1]; // 构建输出数组 for (int i = arr.size() - 1; i >= 0; i--) { output[count[(arr[i] / exp) % 10] - 1] = arr[i]; count[(arr[i] / exp) % 10]--; } // 复制回原数组 for (int i = 0; i < arr.size(); i++) arr[i] = output[i];
} void radixsort(std::vector<int>& arr) { int maxVal = *std::max_element(arr.begin(), arr.end()); // 找到最大数的位数 int exp = 1; while (maxVal / exp > 0) { countingSort(arr, exp); exp *= 10; }
} 或者
#include <iostream>
#include <cmath>
#include <algorithm> // 使用std::max来找到数组中的最大值 // 获取数组中的最大值
int getMax(int arr[], int n) { int mx = arr[0]; for (int i = 1; i < n; i++) { if (arr[i] > mx) { mx = arr[i]; } } return mx;
} // 基数排序函数
void radixsort(int arr[], int n) { // 找到数组中的最大值 int maxVal = getMax(arr, n); // 基数排序使用计数排序作为子程序 // 这里为了简单起见,我们假设所有的整数都是非负的 // 如果有负数,需要做适当的转换 // 对每一位执行计数排序 for (int exp = 1; maxVal / exp > 0; exp *= 10) { int output[n]; // 输出数组 int count[10] = {0}; // 计数器数组 // 存储每个元素的频次 for (int i = 0; i < n; i++) { int index = (arr[i] / exp) % 10; count[index]++; } // 更改count[i]的值,这样它现在包含位置i处之前的所有元素 for (int i = 1; i < 10; i++) { count[i] += count[i - 1]; } // 生成输出数组 for (int i = n - 1; i >= 0; i--) { int index = (arr[i] / exp) % 10; output[count[index] - 1] = arr[i]; count[index]--; } // 将排序后的元素复制回原数组 for (int i = 0; i < n; i++) { arr[i] = output[i]; } }
} int main() { int arr[] = {170, 45, 75, 90, 802, 24, 2, 66}; int n = sizeof(arr) / sizeof(arr[0]); radixsort(arr, n); std::cout << "Sorted array: \n"; for (int i = 0; i < n; i++) { std::cout << arr[i] << " "; } std::cout << std::endl; return 0;
}
相关文章:

常见的8种排序(含代码):插入排序、冒泡排序、希尔排序、快速排序、简单选择排序、归并排序、堆排序、基数排序
时间复杂度O(n^2) 1、插入排序 (Insertion Sort) 从第一个元素开始,该元素可以认为已经被排序;取出下一个元素,在已经排序的元素序列中从后向前扫描;如果该元素(已排序)大于新元素,将该元素移到…...

go语言day2
使用cmd 中的 go install ; go build 命令出现 go cannot find main module 错误怎么解决? go学习-问题记录(开发环境)go: cannot find main module; see ‘go help modules‘_go: no flags specified (see go help mod edit)-CSDN博客 在本…...
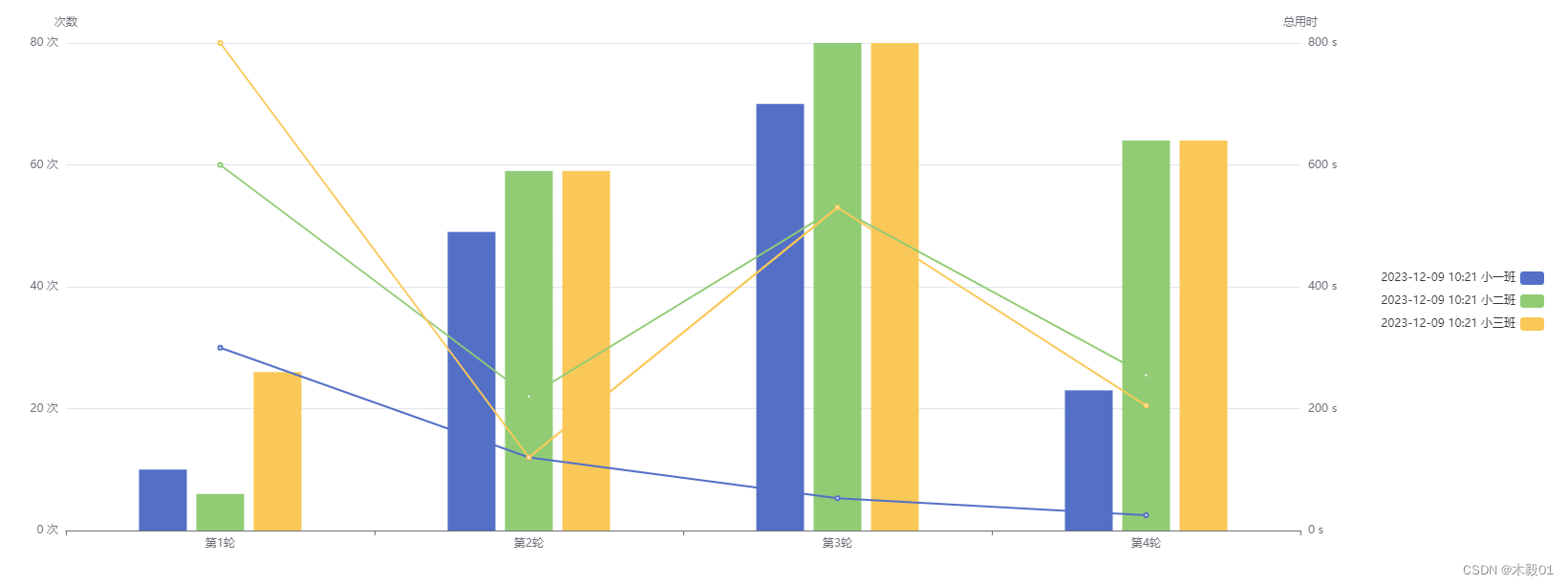
vue echarts画多柱状图+多折线图
<!--多柱状图折线图--> <div class"echarts-box" id"multiBarPlusLine"></div>import * as echarts from echarts;mounted() {this.getMultiBarPlusLine() },getMultiBarPlusLine() {const container document.getElementById(multiBar…...

cesium for unity 打包webgl失败,提示不支持
platform webgl is not supported with HDRP use the Vulkan graphics AR instead....

python开发基础——day7 序列类型方法
一、初识序列类型方法 序列类型的概念:数据的集合,在序列类型里面可以存放任意的数据,也可以对数据进行更方便的操作,这个操作是叫增删改查(crud) ( 增加(Creat),读取查询(Retrieve),更新(Update)…...

用java写一个二叉树翻转
class TreeNode {int val;TreeNode left, right;TreeNode(int val) {this.val val;left right null;} }public class BinaryTree {TreeNode root;// 递归翻转二叉树public TreeNode invertTree(TreeNode root) {if (root null) {return null;}// 递归翻转左子树和右子树Tre…...

数学建模系列(3/4):典型建模方法
目录 引言 1. 回归分析 1.1 线性回归 基本概念 Matlab实现 1.2 多元回归 基本概念 Matlab实现 1.3 非线性回归 基本概念 Matlab实现 2. 时间序列分析 2.1 时间序列的基本概念 2.2 移动平均 基本概念 Matlab实现 2.3 指数平滑 基本概念 Matlab实现 2.4 ARIM…...

AI播客下载:Machine Learning Street Talk(AI机器学习)
该频道由 Tim Scarfe 博士、Yannic Kilcher 博士和 Keith Duggar 博士管理。 他们做了出色的工作,对每个节目进行了彻底的研究,并与机器学习行业中一些受过最高教育、最全面的嘉宾进行了双向对话。 每一集都会教授一些新内容,并且提供未经过滤…...
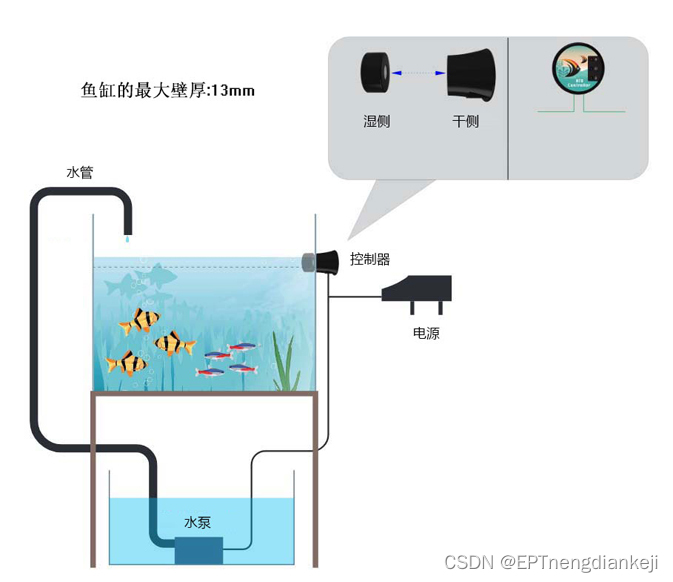
鱼缸补水器工作原理是什么
鱼缸补水器是一种应用广泛的智能设备,主要用于自动监测和补充鱼缸内的水位,以确保鱼类生存环境的稳定。其工作原理简单而高效,为饲主提供了方便和安全的使用体验。 该补水器通常由两部分组成:控制器和吸盘。首先,用户…...

Linux-Tomcat服务配置到系统服务
目录 前言一、系统环境二、配置步骤step1 了解环境的安装路径step2 配置生成tomcat.pid文件step3 配置tomcat.service文件 三、测试systemctl命令管理Tomcat服务3.1 systemctl命令启动Tomcat服务3.2 systemctl命令查看Tomcat服务3.3 systemctl命令关闭Tomcat服务3.4 systemctl命…...

Python抓取高考网图片
Python抓取高考网图片 一、项目介绍二、完整代码一、项目介绍 本次采集的目标是高考网(http://www.gaokao.com/gkpic/)的图片,实现图片自动下载。高考网主页如下图: 爬取的流程包括寻找数据接口,发送请求,解析图片链接,向图片链接发送请求获取数据,最后保存数据。 二…...

Vue配置项data
data 目录 data 目录类型介绍关键原理编译过程 Vue2Vue3 📌Vue.js 中的 data(Obj/Function)属性是 Vue 实例的一个配置选项 类型介绍 对象式 对于根实例或者非复用组件,通常直接提供一个对象字面量作为 data 的值。在对象式中…...
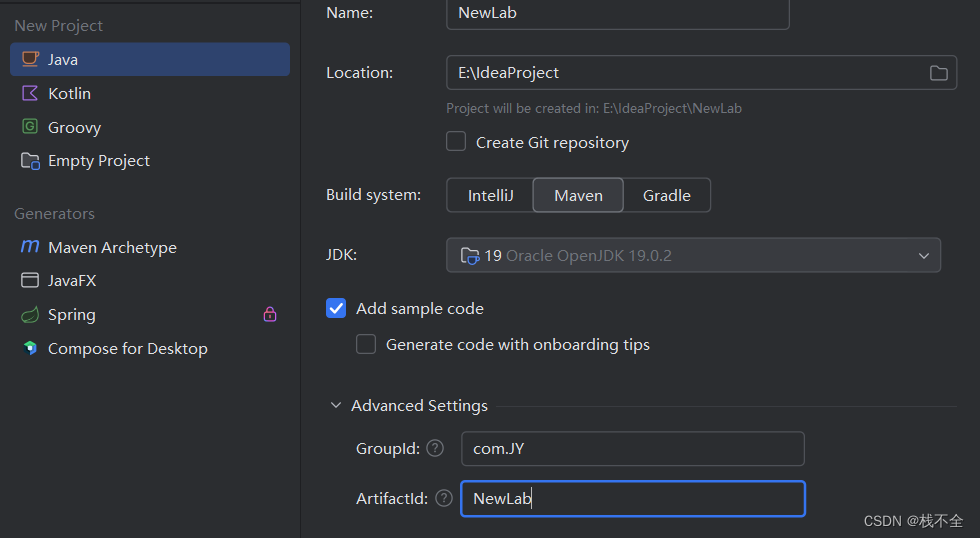
在IDEA 2024.1.3 (Community Edition)中创建Maven项目
本篇博客承继自博客:Windows系统Maven下载安装-CSDN博客 Maven版本:maven-3.9.5 修改设置: 首先先对Idea的Maven依赖进行设置;打开Idea,选择“Costomize”,选择最下边的"All settings" 之后找…...

动手学深度学习(Pytorch版)代码实践 -卷积神经网络-28批量规范化
28批量规范化 """可持续加速深层网络的收敛速度""" import torch from torch import nn import liliPytorch as lp import matplotlib.pyplot as pltdef batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):""&quo…...
Apache Paimon系列之:Append Table和Append Queue
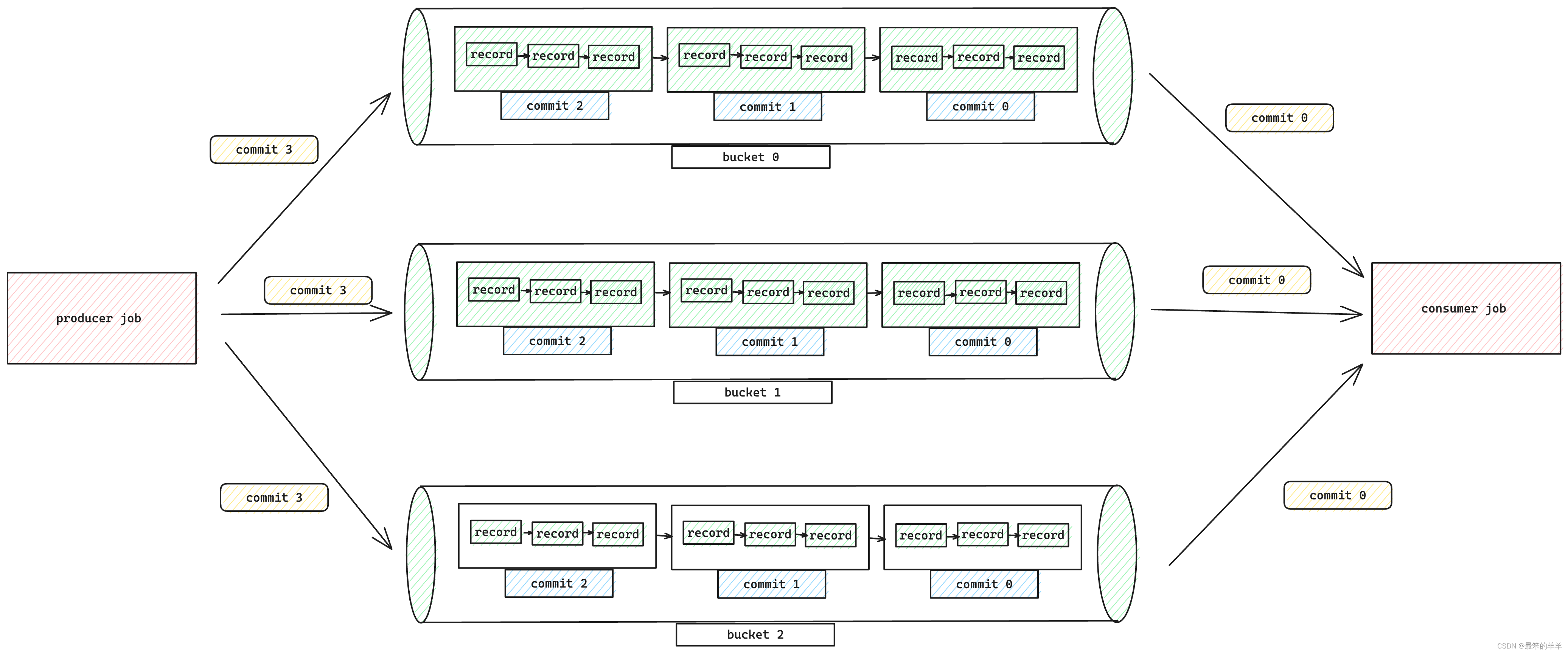
Apache Paimon系列之:Append Table和Append Queue 一、Append Table二、Data Distribution三、自动小文件合并四、Append Queue五、压缩六、Streaming Source七、Watermark Definition八、Bounded Stream 一、Append Table 如果表没有定义主键,则默认为…...

Vue使用vue-esign实现在线签名 加入水印
Vue在线签名 一、目的二、样式三、代码1、依赖2、代码2.1 在线签名组件2.1.1 基础的2.1.2 携带时间水印的 2.2父组件 一、目的 又来了一个问题,直接让我在线签名(还不能存储base64),并且还得上传,我直接***违禁词。 好…...

与码无关:分数限制下,选好专业还是选好学校?
本文的目标读者:24届的高考生和家长。 写这篇非技术性文章,是因为我看到了24届考生和21年的我同样迷茫。 事先声明,本文带有强烈的个人思考色彩,可能会引起不适,如有不同观点,欢迎在评论区讨论。 一、前言…...

什么是负载均衡技术?
随着网络技术的快速发展,互联网行业也越来越广泛,人们的日常生活中也离不开网络技术,大量的用户进行浏览访问网站时,企业会使用负载均衡技术,降低当前网站的负载,以此来提高网站的访问速度。 今天小编就来给…...

存在重复元素Ⅱ python3
存在重复元素Ⅱ 问题描述解题思路代码实现复杂度 问题描述 给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] nums[j] 且 abs(i - j) < k 。如果存在,返回 true ;否则ÿ…...
【CV炼丹师勇闯力扣训练营 Day13:§6二叉树1】
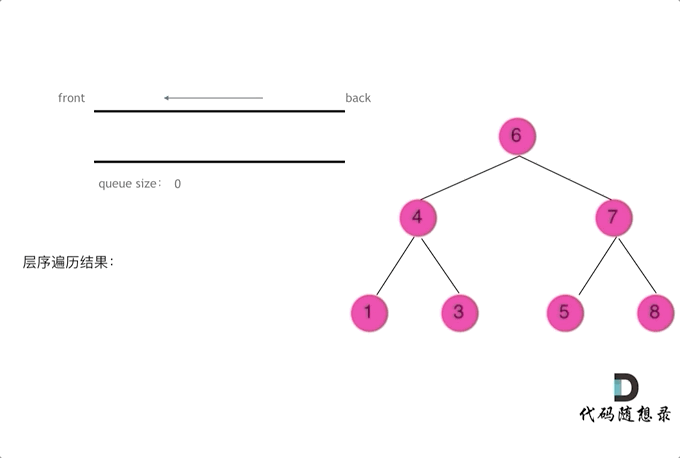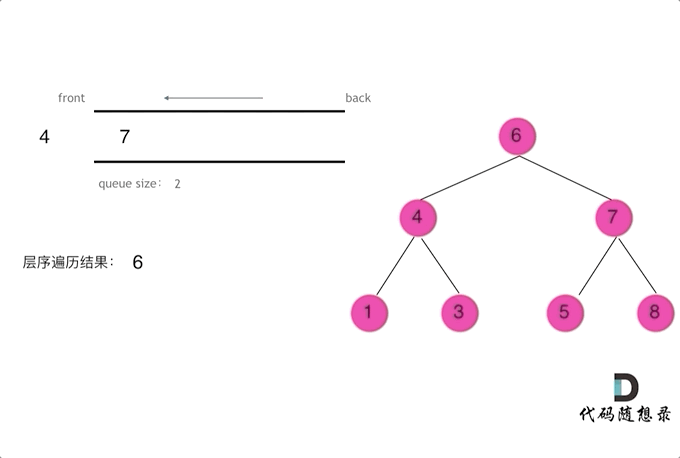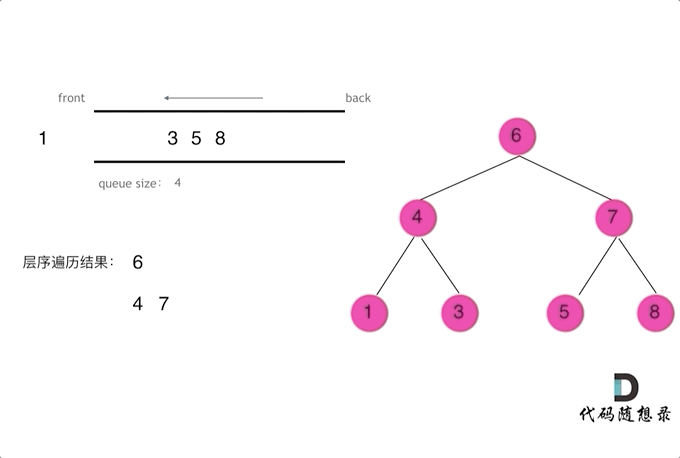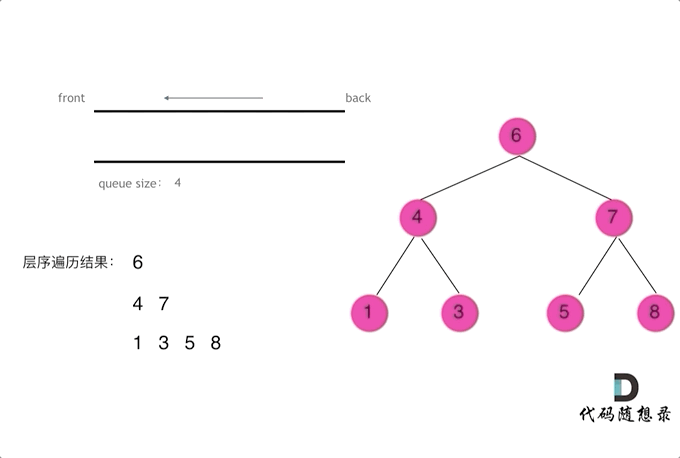
CV炼丹师勇闯力扣训练营 代码随想录算法训练营第13天 二叉树的递归遍历 二叉树的迭代遍历、统一迭代 二叉树的层序遍历 一、二叉树的递归遍历(深度优先搜索) 【递归步骤】 1.确定递归函数的参数和返回值:确定哪些参数是递归的过程中需要处理…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
