力扣第一道困难题《3. 无重复字符的最长子串》,c++
目录
方法一:
方法二:
方法三:
方法四:
没有讲解,但给出了优秀题解
本题链接:4. 寻找两个正序数组的中位数 - 力扣(LeetCode)

话不多说,我们直接开始进行本题的思路解析;
首先我们看到这个题是肯定有一种暴力的硬解思路的,
方法一:
那就是将两个vector直接链接起来,然后再排序后,直接返回中间值,这个方法实现起来还是非常容易的,
代码如下:
class Solution { public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2){size_t n = nums1.size();size_t m = nums2.size();if (m == 0){if (n % 2 == 0)return (nums1[n / 2 - 1] + nums1[n / 2]) / 2.0;elsereturn nums1[n / 2];}if (n == 0){if (m % 2 == 0)return (nums2[m / 2 - 1] + nums2[m / 2]) / 2.0;elsereturn nums2[m / 2];}size_t sum = m + n;int* nums = new int[m + n];int count = 0, i = 0, j = 0;while (count != sum){if (i == n){while (j != m)nums[count++] = nums2[j++];break;}if (j == m){while (i != n)nums[count++] = nums1[i++];break;}if (nums1[i] > nums2[j])nums[count++] = nums2[j++];elsenums[count++] = nums1[i++];}if (count % 2 == 0)return (nums[count / 2 - 1] + nums[count / 2]) / 2.0;elsereturn nums[count / 2];} };int main() {vector<int> s1;vector<int> s2;s1.push_back(1);s1.push_back(2);s2.push_back(3);s2.push_back(4);s2.push_back(5);s2.push_back(6);Solution s;cout << s.findMedianSortedArrays(s1, s2) << endl;return 0; }首先这个代码是可以编译成功的,
这里也有一个小技巧,如果这个代码是为0,那么证明编译时没有问题的,如果是非0,那么就是编译有问题,还需要修改代码。
但是会过来这个代码再力扣上是运行超时的,因为题目要求的时间复杂度是O(log (m+n))
但是我们的时间复杂度是O(m+n)
空间复杂度也是O(m+n)
方法二:
其实我们的方法一是我们真正的将两个vector真正的链接在了一起,但实际上我们这一步可以省略,我们只需要挨个比较得到第k(假设中位数为第k位)个大的数是多少,那么其实就得到了中位数是多少。其实这一题方便了一点,题目给的数组是已有序的,所以我们挨个比较就行
开始我们写一个循环,这个循环我们的目的就是找到中位数所对应的下标是多少,如果找到了,那么就返回他的下标值,还没找到,那么就继续。但是这样来说,对偶数和奇数的分类会很麻烦。当其中一个数组遍历完后,还要分好几种情况进行另类判断另一个数组,这样想起来都麻烦。
然而要进行优化,那么我们就需要找到要进行优化的部分,那么就是考虑对偶与奇的情况不分开讨论,进行合并考虑,对于此情况我们可以在另定义两个变量left与right分别保存左操作数与右操作数。
假设合并的数组长度为len,那么无论对应偶还是奇,我们只需要遍历前 len/2+1 个数就可以(如果是偶数,我们需要知道第 len/2和 len/2+1 个数,也是需要遍历 len/2+1 次。所以遍历的话,奇数和偶数都是 len/2+1 次。)
返回的left与right我们要做到如果是奇,那么只需要right,如果是偶,因为left不等于right,所以返回两个数的平均数;所以我们在for循环里应该保证依次循环过后left与right差一个位,所以我们要先在循环开始将right的值赋给left,后进行调整right。
然后写出大致框架:
如果nums1[i]<nums2[i],那么就将nums1[i]赋值给right,反之nums2[i];
我们在调整right的时候首先要考虑的就是nums是否越界,所以我需要先判断是否越界,同理考虑了nums1也需要考虑nums2;
所以填充完代码如下:
class Solution { public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size();int n = nums2.size();int len = m + n;int left = -1, right = -1;int aStart = 0, bStart = 0;for (int i = 0; i <= len / 2; i++) {left = right;//调整rightif (aStart < m && (bStart >= n || nums1[aStart] < nums2[bStart])) {right = nums1[aStart++];}else {right = nums2[bStart++];}}if ((len % 2) == 0)return (left + right) / 2.0;elsereturn right;} }; int main() {vector<int> s1;vector<int> s2;s1.push_back(1);s1.push_back(2);s2.push_back(3);s2.push_back(4);s2.push_back(5);s2.push_back(6);Solution s;cout << s.findMedianSortedArrays(s1, s2) << endl;return 0; }
运行起来是正确的,但依然在力扣上是不行的,还是运行超时;
时间复杂度是:遍历了m+n/2+1个数,但时间复杂度还是O(m+n);
方法三:
我第一眼看到这个题的时候,首先想到的就是二分查找,然后就想到了分别对两个数组进行二分,但是如果nums2全都大于num1那么这样就不行,然后我在看了别人的题解后然后理解了理解,就大为震撼,妙,但是题解是java的然后我自己又写了写修改了好几次终于写出来了。
方法二中,我们一次遍历就相当于去掉不可能是中位数的一个值,也就是一个一个排除。由于数列是有序的,其实我们完全可以一半儿一半儿的排除。假设我们要找第 k 小数,我们可以每次循环排除掉 k/2 个数。方法三其实与方法二同理,也是主要找到第k个数是多少。
下面我们看一个例子


此时3=3
然后我们需要将两个数组的第 k/2 个数进行比较 ,然后将小的那个数组前k/2个数舍弃,对于方便处理,我们设定如果两个数相等,目前我们先优先删除第二个数组删除;(后面代码是是先有限舍弃第一个数组,这里是为了避开特殊情况)
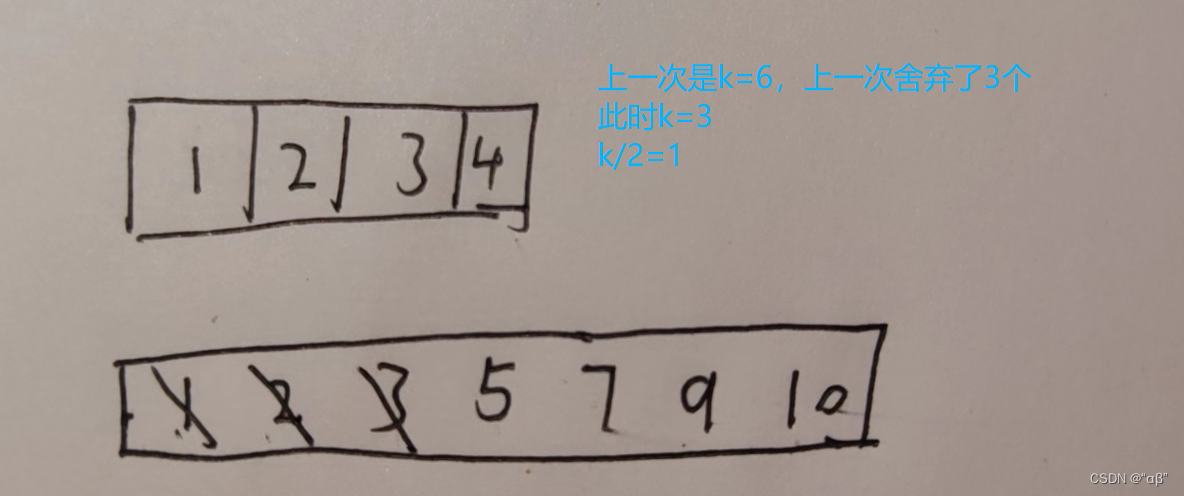

此时1<5
这次舍弃num1 的 k/2 个数;


此时2<5
同理,继续舍弃nums1,舍弃 k/2 个数
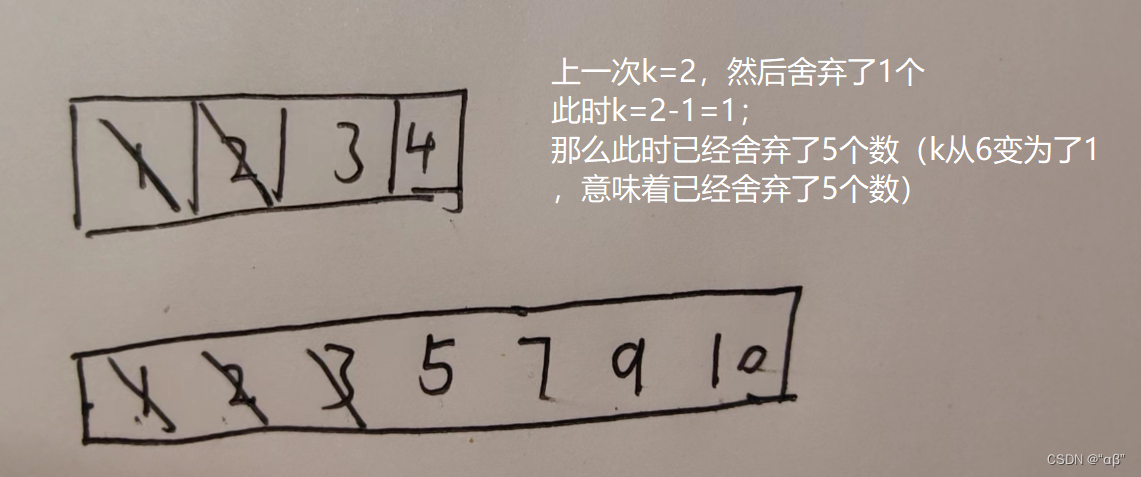
 这时候3<5;这时候3就为第6大的数,就是中位数。
这时候3<5;这时候3就为第6大的数,就是中位数。
这个方法是不是很妙呢?
然后我们就刷刷的写,然后突然就有一个案例不通过,那就是
如果按照上面的方法进行按照步骤进行梳理,那么就会发现第一步的时候就会卡住,因为第一步我么要进行舍弃的数的个数就已经超出了nums1的长度,直接会越界,那么这时候我们就需要进行特殊处理,如果舍弃个数大于剩余长度,那么就舍弃剩余长度。
思路全部梳理完后,如果对递归熟悉的话,那么就完全可以写出来,思路难想,但是代码实现还是比较简单的。(特殊案例我也进行处理了,后面会进行特别分析)
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();int m = nums2.size();int left = (n + m + 1) / 2;int right = (n + m + 2) / 2;return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;}int getKth(vector<int>& nums1, int start1, int end1, vector<int>& nums2, int start2, int end2, int k){//舍弃k/2个//结束条件k==1int len1 = end1 - start1 + 1;int len2 = end2 - start2 + 1;//让 len1 的长度小于 len2,这样就能保证如果有数组空了,一定是 len1 if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);//还存在一种情况,就是k不为1的情况下,但len1已经等于0if (len1 == 0) return nums2[start2 + k - 1]; if (k == 1)return min(nums1[start1], nums2[start2]);int i = start1 + min(len1, k / 2) - 1;int j = start2 + min(len2, k / 2) - 1;if (nums1[i] > nums2[j]){return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));}else{return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));}}
};到此我们就出来了第一种在力扣上通过的代码;
然后进行特别分析
1:
这一步也是跟方法二同样的找到求中位数的操作数第left是第几个,right是第几个;与之不同的就是奇的情况下left=right,偶的情况下left+1=right;
2:
此案例对应的也就是
在求right的时候k=7;先舍弃k/2=3个
此时k=4;
然后再舍弃的话num1已经没有了但是k=4-2=2;还不为1;如果返回的还要再舍弃的话,就会报错越界;
所以要加特殊情况处理
3: 
这一步也是为了对应2,方便,如果没有这个,那么就有可能len2先空的情况,所以这一步避免了分类讨论;
最后再展示一边代码:
class Solution { public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();int m = nums2.size();int left = (n + m + 1) / 2;int right = (n + m + 2) / 2;return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;}int getKth(vector<int>& nums1, int start1, int end1, vector<int>& nums2, int start2, int end2, int k){//舍弃k/2个//结束条件k==1int len1 = end1 - start1 + 1;int len2 = end2 - start2 + 1;//让 len1 的长度小于 len2,这样就能保证如果有数组空了,一定是 len1 if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);//还存在一种情况,就是k不为1的情况下,但len1已经等于0if (len1 == 0){return nums2[start2 + k - 1];}if (k == 1)return min(nums1[start1], nums2[start2]);int i = start1 + min(len1, k / 2) - 1;int j = start2 + min(len2, k / 2) - 1;if (nums1[i] > nums2[j]){return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));}else{return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));}} };运行成功
时间复杂度是
O(log (m+n))。符合要求
方法四:
但是这个方法三还是效率不是很高, 
其实还有一种更牛的方法,但本人看了看看不明白,运用到了统计学;本人还没有学统计学,能看明白一点,但是还是看清楚;
我看了题解有两种一个数官方一个是别的作者大佬写的;本人推荐大佬,官方直接给了题目解释,没有给知识补充;
4. 寻找两个正序数组的中位数 - 力扣(LeetCode)
为了方便这里给出了全部官方截图:

最后这个题就已经完全讲解完了,第一次完全写完力扣困难题,总的来说是很难,但不至于一点思路也没有,而且写的过程中思考是很多的,还是比简单题写起来吃力。有能力还是多写困难题;
相关文章:

力扣第一道困难题《3. 无重复字符的最长子串》,c++
目录 方法一: 方法二: 方法三: 方法四: 没有讲解,但给出了优秀题解 本题链接:4. 寻找两个正序数组的中位数 - 力扣(LeetCode) 话不多说,我们直接开始进行本题的思路解…...

【ai】tx2 nx :ubuntu查找NvInfer.h 路径及哪个包、查找符号
在Ubuntu系统中,你可以使用多种方法来查找某个头文件的路径。这里有几种常用的方法: 使用find命令: find命令是一个非常强大的工具,可以在文件系统中搜索匹配特定条件的文件。例如,如果你想查找名为stdio.h的头文件,可以使用以下命令:bash 复制代码 sudo find / -name …...

C++ 运算符的优先级和结合性表
优先级和结合性表 优先级运算符描述结合性1::作用域解析运算符左到右2() [] . -> --后缀运算符左到右3 -- - ! ~ * & sizeof new delete typeid一元运算符右到左4* / %乘除取模左到右5 -加法和减法左到右6<< >>左移和右移左到右7< < > >关系…...

MySQL中SQL语句的执行过程详解
1. 客户端连接和请求 客户端连接 在MySQL中,客户端连接和请求过程是执行SQL语句的第一步。该步骤主要涉及客户端如何连接到MySQL服务器,以及如何维护和管理客户端与服务器之间的会话。 客户端连接: 连接器(Connector)…...
文心一言4.0免费使用
领取&安装链接:Baidu Comate 领取季卡 视频教程:免费使用文心一言4.0大模型_哔哩哔哩_bilibili 有图有真相 原理:百度comate使用文心一言最新的4.0模型。百度comate目前免费使用,可以借助comate达到免费使用4.0模型目的。 …...
Mongodb安装与配置
Mongodb的下载 这里下载的是MongoDB 7.0.11版本的 首先进入官网:https://www.mongodb.com/ 点击完上面两步后,加载来到该页面,选择自己的版本、系统,是压缩包(zip)还是安装包(msi)。 下载好之后能,来到安装包哪里&a…...

Java校园跑腿小程序校园代买帮忙外卖源码社区外卖源码
🔥校园跑腿与外卖源码揭秘🔥 🚀 引言:为何需要校园跑腿与外卖源码? 在快节奏的校园生活里,学生们对于便捷、高效的服务需求日益增长。校园跑腿和外卖服务成为了解决这一需求的热门选择。然而,…...

MySQL高级-MVCC-基本概念(当前读、快照读)
文章目录 1、MVCC基本概念1.1、当前读1.1.1、创建表 stu1.1.2、测试 1.2、快照读 1、MVCC基本概念 全称Multi-Version Concurrency Control,多版本并发控制。指维护一个数据的多个版本,使得读写操作没有冲突,快照读为MySQL实现MVCC提供了一个…...
kubernetes给指定用户分配调用k8s的api权限
文章目录 概要利用RBAC添加角色权限使用shell命令创建角色权限使用配置文件创建角色权限 调用k8s的api获取k8s账户的token 小结 概要 使用kubernetes部署项目时,有些特殊场景,我们需要在自己创建的pod里面调用k8s的api来管理k8s,但是需要使用…...

无人机的弱点和限制
1.电池和续航能力: 续航时间短:大多数无人机依赖锂电池供电,续航时间通常在30分钟至1小时之间,限制了其长时间任务的执行能力。 能量密度低:现有电池技术的能量密度无法满足长时间飞行需求,需要突破性的发…...

ElementUI的基本搭建
目录 1,首先在控制终端中输入下面代码:npm i element-ui -S 安装element UI 2,构架登录页面,login.vue编辑 3,在官网获取对应所需的代码直接复制粘贴到对应位置 4,在继续完善,从官网添加…...
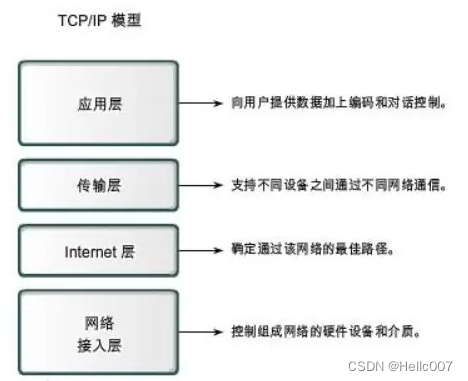
Modbus TCP与TCP/IP协议间的差异与应用场景
Modbus TCP概述 Modbus协议简介 Modbus是一种专为工业自动化系统设计的通信协议,采用主从模式,即一个主设备(通常是计算机或可编程逻辑控制器)与多个从设备(如传感器、执行器等)进行通信。Modbus协议具有…...
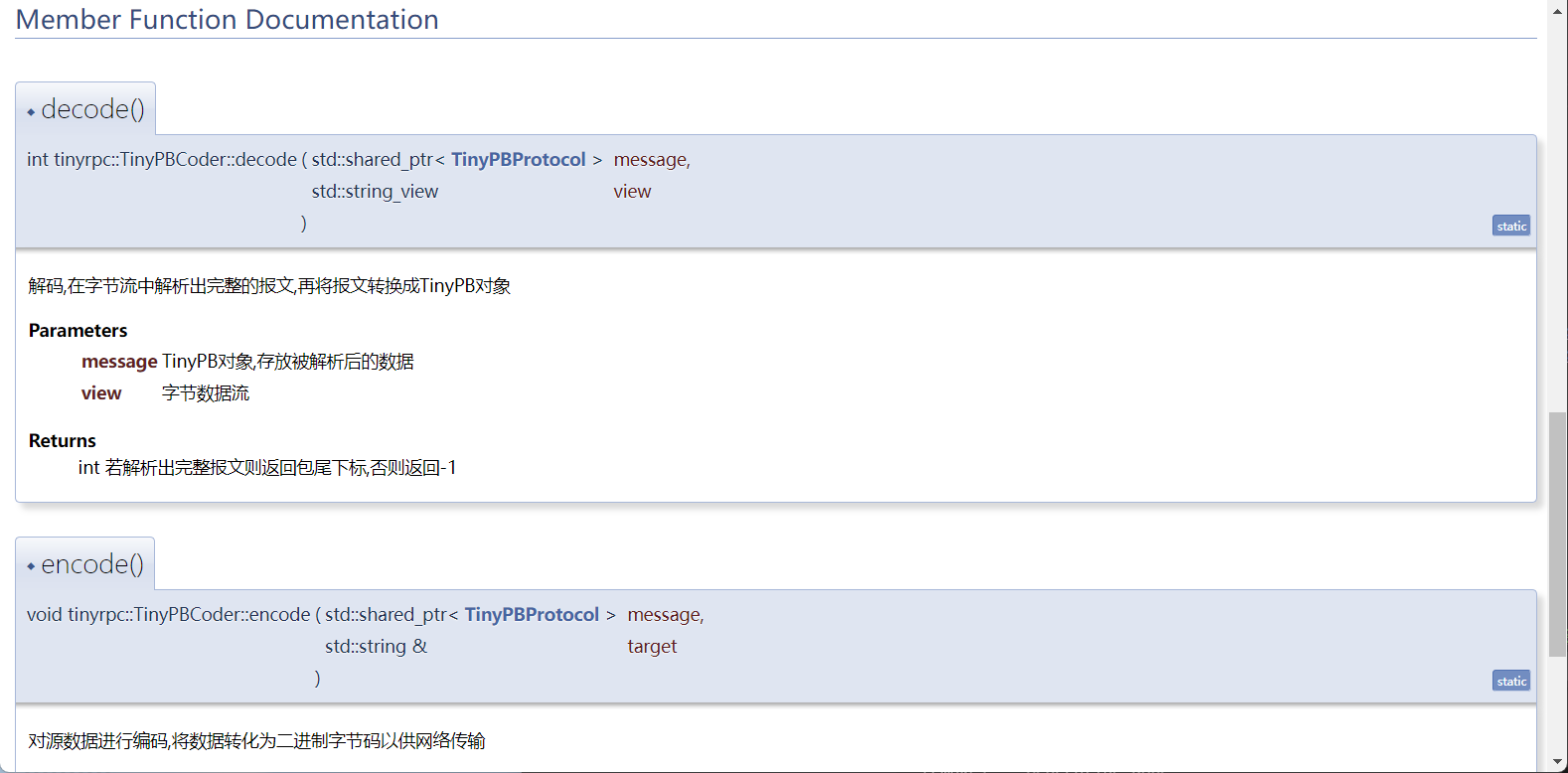
Linux Doxygen快速生成文档
此前写过一篇编写Doxygen格式的注释以用于生成文档,点击以查阅, Doxygen常用语法与字段记录,但是当时用的windows桌面版的doxygen,最近使用ubuntu编写代码想直接使用doxygen生成,故写下此博客 Doxygen Doxygen是一个用于生成软件文档的工具,它可以从代码中提取注释…...

MobPush REST API的推送 API之批量推送
调用验证 详情参见 REST API 概述的 鉴权方式 说明。 频率控制 详情参见推送限制策略的 接口限制 说明。 调用地址 POST http://api.push.mob.com/v3/push/createMulti 推送对象 以 JSON 格式表达,表示一条推送相关的所有信息 字段类型必须说明pushWorkobje…...

Arthas快速入门
简介 Arthas 是一款线上监控诊断产品,通过全局视角实时查看应用 load、内存、gc、线程的状态信息,并能在不修改应用代码的情况下,对业务问题进行诊断,包括查看方法调用的出入参、异常,监测方法执行耗时,类…...
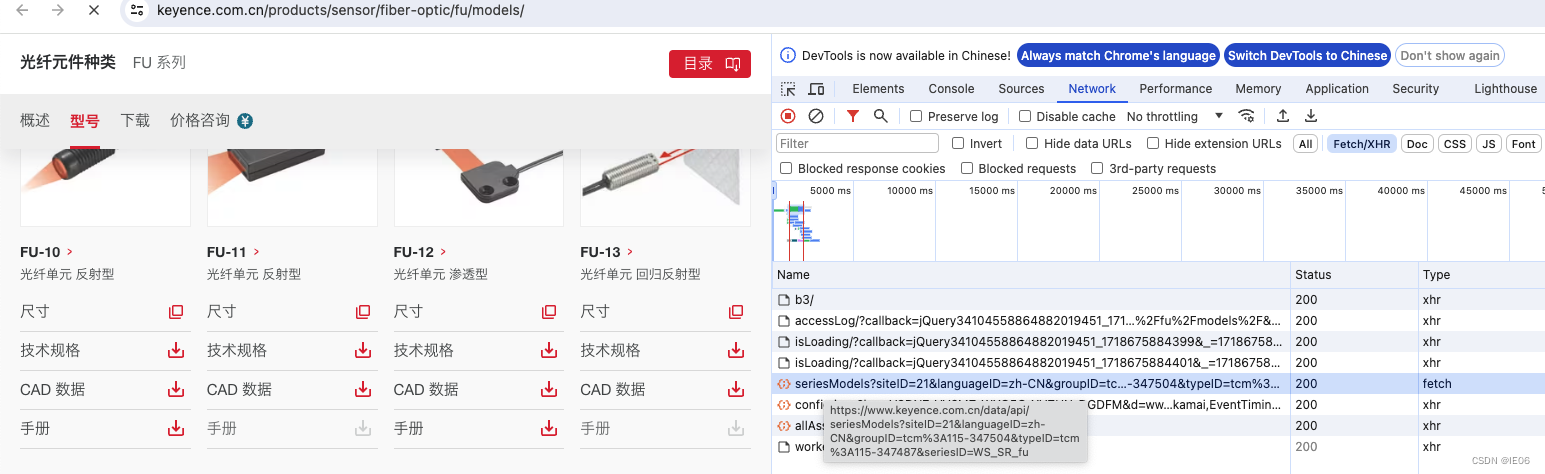
python系列30:各种爬虫技术总结
1. 使用requests获取网页内容 以巴鲁夫产品为例,可以用get请求获取内容: https://www.balluff.com.cn/zh-cn/products/BES02YF 对应的网页为: 使用简单方法进行解析即可 import requests r BES02YF res requests.get("https://www.…...

PHP和phpSpider:如何应对反爬虫机制的封锁?
php和phpspider:如何应对反爬虫机制的封锁? 引言: 随着互联网的快速发展,对于大数据的需求也越来越大。爬虫作为一种抓取数据的工具,可以自动化地从网页中提取所需的信息。然而,由于爬虫的存在,…...
学生宿舍管理系统
摘 要 随着高校规模的不断扩大和学生人数的增加,学生宿舍管理成为高校日常管理工作中的重要组成部分。传统的学生宿舍管理方式往往依赖于纸质记录和人工管理,这种方式不仅效率低下,而且容易出错,无法满足现代高校管理的需求。因此…...

一分钟彻底掌握Java迭代器Iterator
Iterator Iterator 是 Java 的 java.util 包中的一个接口 iterator() 是 Java 集合框架中的一个方法,它返回一个 Iterator 对象,该对象可以用来遍历集合中的元素。 Iterator确实是一个接口,你不能直接实例化一个接口。但是,你可以…...

第三十七篇——麦克斯韦的妖:为什么要保持系统的开放性?
目录 一、背景介绍二、思路&方案三、过程1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇文章结合我知道的东西我能想到什么? 四、总结五、升华 一、背景介绍 如果没有详细的学习这篇文章,我觉得我就是被麦克斯韦妖摆弄的…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...


