maven 依赖冲突
依赖冲突
1、对于 Maven 而言,同一个 groupId 同一个 artifactId 下,只能使用一个 version。
<!-- https://mvnrepository.com/artifact/org.apache.commons/commons-math3 --><dependency><groupId>org.apache.commons</groupId><artifactId>commons-math3</artifactId><version>3.6.1</version></dependency><!-- 只会使用 3.6 这个版本的依赖 --><dependency><groupId>org.apache.commons</groupId><artifactId>commons-math3</artifactId><version>3.6</version></dependency>若相同类型但版本不同的依赖存在于同一个 pom 文件,只会引入后一个声明的依赖。

2、项目的两个依赖同时引入了某个依赖。
- 最短路径优先(Nearest Definition Wins):即优先选择依赖树中离项目最近的版本。
- 先声明者优先(First Declaration Wins):即优先选择在
pom.xml中首次声明的依赖版本。
举个例子,项目存在下面这样的依赖关系:
依赖链路一:A -> B -> C -> X(1.0)
依赖链路二:A -> D -> X(2.0)
这两条依赖路径上有两个版本的 X,为了避免依赖重复,Maven 只会选择其中的一个进行解析。
哪个版本的 X 会被 Maven 解析使用呢?
Maven 在遇到这种问题的时候,会遵循 路径最短优先 和 声明顺序优先 两大原则。解决这个问题的过程也被称为 Maven 依赖调解 。
最短路径优先:
依赖链路一:A -> B -> C -> X(1.0) // dist = 3
依赖链路二:A -> D -> X(2.0) // dist = 2
依赖链路二的路径最短,因此,X(2.0)会被解析使用。
不过,你也可以发现。路径最短优先原则并不是通用的,像下面这种路径长度相等的情况就不能单单通过其解决了:
先声明者优先:举个例子,项目存在下面这样的依赖关系:
依赖链路一:A -> B -> X(1.0)
依赖链路二:A -> D -> X(2.0)
这两条依赖路径上有两个版本的 X,为了避免依赖重复,Maven 只会选择其中的一个进行解析。
<!-- A pom.xml -->
<dependencies>...dependency B...dependency D
</dependencies>
在依赖路径长度相等的前提下,在 pom.xml 中依赖声明的顺序决定了谁会被解析使用,顺序最前的那个依赖优胜。该例中,如果 B 的依赖声明在 D 之前,那么 X (1.0)就会被解析使用。
排除依赖
单纯依赖 Maven 来进行依赖调解,在很多情况下是不适用的,需要我们手动排除依赖。
举个例子,当前项目存在下面这样的依赖关系:
依赖链路一:A -> B -> C -> X(1.5) // dist = 3
依赖链路二:A -> D -> X(1.0) // dist = 2
根据路径最短优先原则,X(1.0) 会被解析使用,也就是说实际用的是 1.0 版本的 X。
但是!这会一些问题:如果 D 依赖用到了 1.5 版本的 X 中才有的一个类,运行项目就会报NoClassDefFoundError错误。如果 D 依赖用到了 1.5 版本的 X 中才有的一个方法,运行项目就会报NoSuchMethodError错误。
现在知道为什么你的 Maven 项目总是会报NoClassDefFoundError和NoSuchMethodError错误了吧?
如何解决呢? 我们可以通过exclusion标签手动将 X(1.0) 给排除。
<dependency>......<exclusions><exclusion><artifactId>x</artifactId><groupId>org.apache.x</groupId></exclusion></exclusions>
</dependency>
一般在解决依赖冲突的时候,都会优先保留版本较高的。这是因为大部分 jar 在升级的时候都会做到向下兼容。
如果高版本修改了低版本的一些类或者方法的话,这个时候就能直接保留高版本了,而是应该考虑优化上层依赖,比如升级上层依赖的版本。
还是上面的例子:
依赖链路一:A -> B -> C -> X(1.5) // dist = 3
依赖链路二:A -> D -> X(1.0) // dist = 2
保留了 1.5 版本的 X,但是这个版本的 X 删除了 1.0 版本中的某些类。这个时候,可以考虑升级 D 的版本到一个 X 兼容的版本。
更多消息资讯,请访问昂焱数据。
相关文章:

maven 依赖冲突
依赖冲突 1、对于 Maven 而言,同一个 groupId 同一个 artifactId 下,只能使用一个 version。 <!-- https://mvnrepository.com/artifact/org.apache.commons/commons-math3 --><dependency><groupId>org.apache.commons</groupId&…...

demon drone 200无人机标定流程
demon drone 200无人机标定流程 一、飞控固件更新1.1 固件更新1.2 参数更新 二、imu标定2.1 安装imu标定工具(在你自己的电脑上)2.2 录制rosbag(在对应飞机上)2.3 运行标定程序(在你自己的电脑上) 三、双目及imu联合标定3.1 安装标…...

案例开发-日程管理-第一期
九 案例开发-日程管理-第一期 共7期 9.1 登录页及校验 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><style>.ht{text-align: center;color: cadetblue;font-family: 幼…...

【Java 注解,自定义注解,元注解,注解本质,注解解析】
文章目录 什么是注解?Java内置注解自定义注解元注解注解的本质注解解析 什么是注解? 注解是Java编程语言中的一种元数据,提供了有关程序的额外信息。注解以符号开始,紧跟着注解的名称和一对括号,括号内包含注解的参数…...

染色法判定二分图
什么是二分图? 二分图,也称作二部图,是图论中的一种特殊模型。在一个无向图G(V,E) 中,如果顶点集合 V 可以被分割成两个互不相交的子集 A 和 B,并且图中的每条边 (i,j) 关联的两个顶点 i 和 j 分别属于这两个不同的顶…...

自动气象站的主要功能优势
在科技日新月异的今天,我们生活的方方面面都受到了科技的影响。其中,自动气象站作为气象观测领域的重要一环,不仅提升了气象数据的准确性和时效性,还为我们的日常生活、农业生产、灾害预防等提供了重要的数据支持。 自动气象站概述…...

Java中实现二维数组(矩阵)的转置
在矩阵运算中,矩阵的转置是一个基本操作,即将矩阵的行变成列,列变成行。在Java中,我们可以通过编写一个方法来实现二维数组的转置。下面,我将详细介绍如何在Java中完成这一任务,并提供完整的代码示例。 编…...
Prometheus+Grafana主机运行数据
目录 介绍 安装Node Exporter 配置Prometheus 验证配置 导入仪表盘 介绍 Prometheus是一款开源的监控和警报工具,而Node Exporter是Prometheus的一个官方插件,用于采集主机上的各种系统和硬件指标。 安装Node Exporter 下载最新版本的Node Export…...

GraphQL在Postman中:释放API查询的强大潜能
🚀 GraphQL在Postman中:释放API查询的强大潜能 Postman作为API开发和测试的领先工具,对GraphQL的支持为开发者提供了一种新的方式来查询和管理数据。GraphQL是一种查询语言,用于API,允许客户端明确指定他们需要哪些数…...

大语言模型里的微调vs RAG vs 模板提示词
文章目录 介绍微调(Fine-tuning)定义优点:缺点:应用场景:技术细节 检索增强生成(RAG,Retrieval-Augmented Generation)定义优点:缺点:应用场景:技…...

网络编程:常用网络测试工具
telnet netstat ping arp wireshark(网络抓包工具) tcpdumpssh2 secure crt ——软件工具sudo ufw disable sudo apt-get install openssh-server openssh-client //两个命令敲完 得重启sudo apt-get install wireshark 1、telnet 远程登录工具&…...
mov视频怎么改成mp4?把mov改成MP4的四个方法
mov视频怎么改成mp4?选择合适的视频格式对于确保内容质量和流通性至关重要。尽管苹果公司的mov格式因其出色的视频表现备受赞誉,但在某些情况下,它并非最佳选择,因为使用mov格式可能面临一些挑战。MP4格式在各种设备(如…...

力扣1472.设计浏览器历史记录
力扣1472.设计浏览器历史记录 用双指针记录历史记录 以及栈顶高度移动时会直接把之前的记录消掉 class BrowserHistory {int pos-1;int top0;string history[5010];public:BrowserHistory(string homepage) {visit(homepage);}void visit(string url) {pos ;top pos;histor…...

准大一新生开学千万要带证件照用途大揭秘
1、提前关注好都有哪些考场,以及这些考场大致在网页的哪个位置。比如我选对外经贸大学,我就直接找到第二个点进去。 2、电脑上同时开了谷歌浏览器和IE浏览器,以及手机也登陆了。亲测下来,同一时间刷新,谷歌浏览器能显示…...

QImage显示图片像素
在Qt中,QImage 类是用来表示和处理图像的。如果你想查看或显示一个图片的像素数据,你可以使用 QImage 提供的方法来访问这些数据。以下是一些基本的方法来获取和显示图片的像素信息: 获取图像的像素格式: 使用 QImage::format() …...
uniapp使用高德地图(公众号+h5)
选择微信小程序的话后果就是你的地图出不来,出来了就报key异常 下面直接放配置和代码: 打包后的高德uni-app,uniCloud,serverless,高德地图,申请高德地图Key,配置使用高德地图,参数说明,高德开放平台用户名,百度地图,申请百度地图Key,配置使用百度地图,…...

深度学习与浅层学习:技术变革下的竞争态势
深度学习与浅层学习:技术变革下的竞争态势 在过去十年中,深度学习的崛起对整个人工智能领域产生了巨大影响,几乎在各种任务中显示出超越传统浅层学习方法的性能。这种变化不仅推动了技术的进步,还对硬件市场,尤其是显…...

LeetCode 219. 存在重复元素 II
LeetCode 219. 存在重复元素 II 给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] nums[j] 且 abs(i - j) < k 。如果存在,返回 true ;否则,返回 false 。 示例 1&am…...

【目标检测】使用自己的数据集训练并预测yolov8模型
1、下载yolov8的官方代码 地址: GitHub - ultralytics/ultralytics: NEW - YOLOv8 🚀 in PyTorch > ONNX > OpenVINO > CoreML > TFLite 2、下载目标检测的训练权重 yolov8n.pt 将 yolov8n.pt 放在ultralytics文件夹下 3、数据集分布 注…...
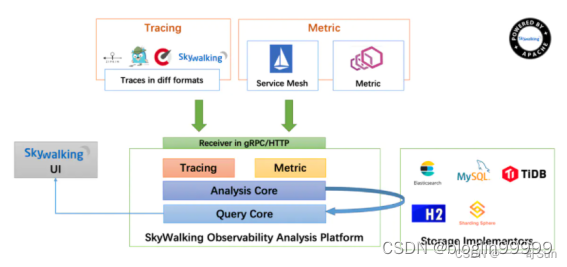
应用监控SkyWalking调研
参考: 链路追踪( Skyworking )_skywalking-CSDN博客 企业级监控项目Skywalking详细介绍,来看看呀-CSDN博客 SkyWalking 极简入门 | Apache SkyWalking 使用 SkyWalking 监控 ClickHouse Server | Apache SkyWalking https://zhuanlan.zhihu.com/p/3…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
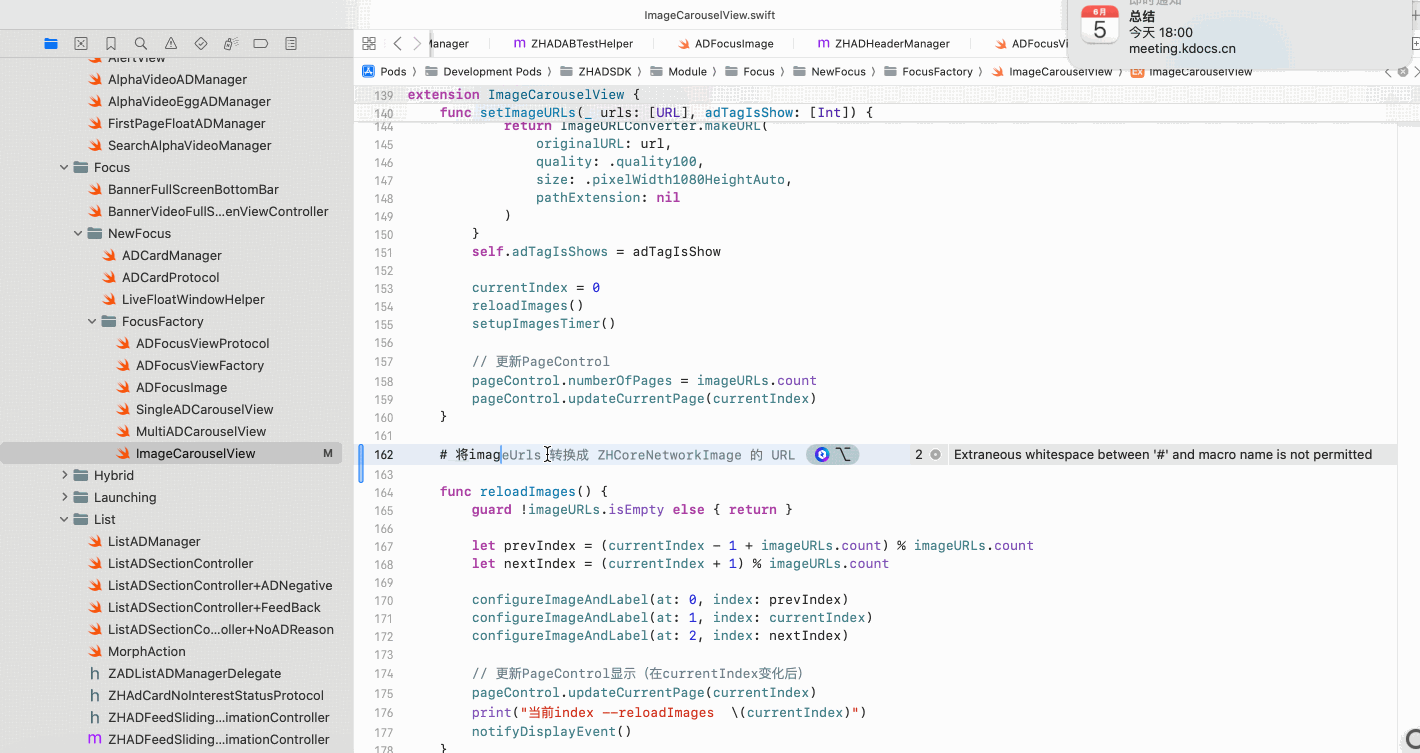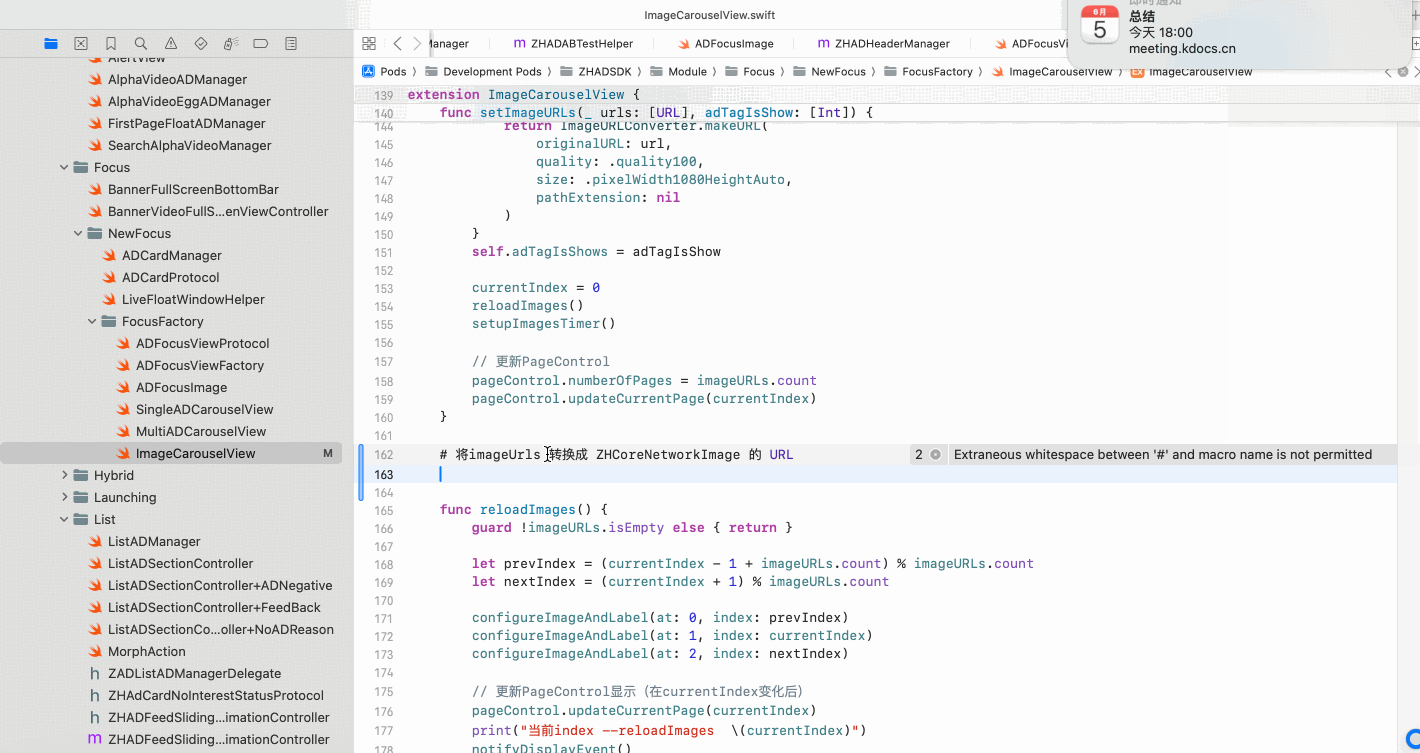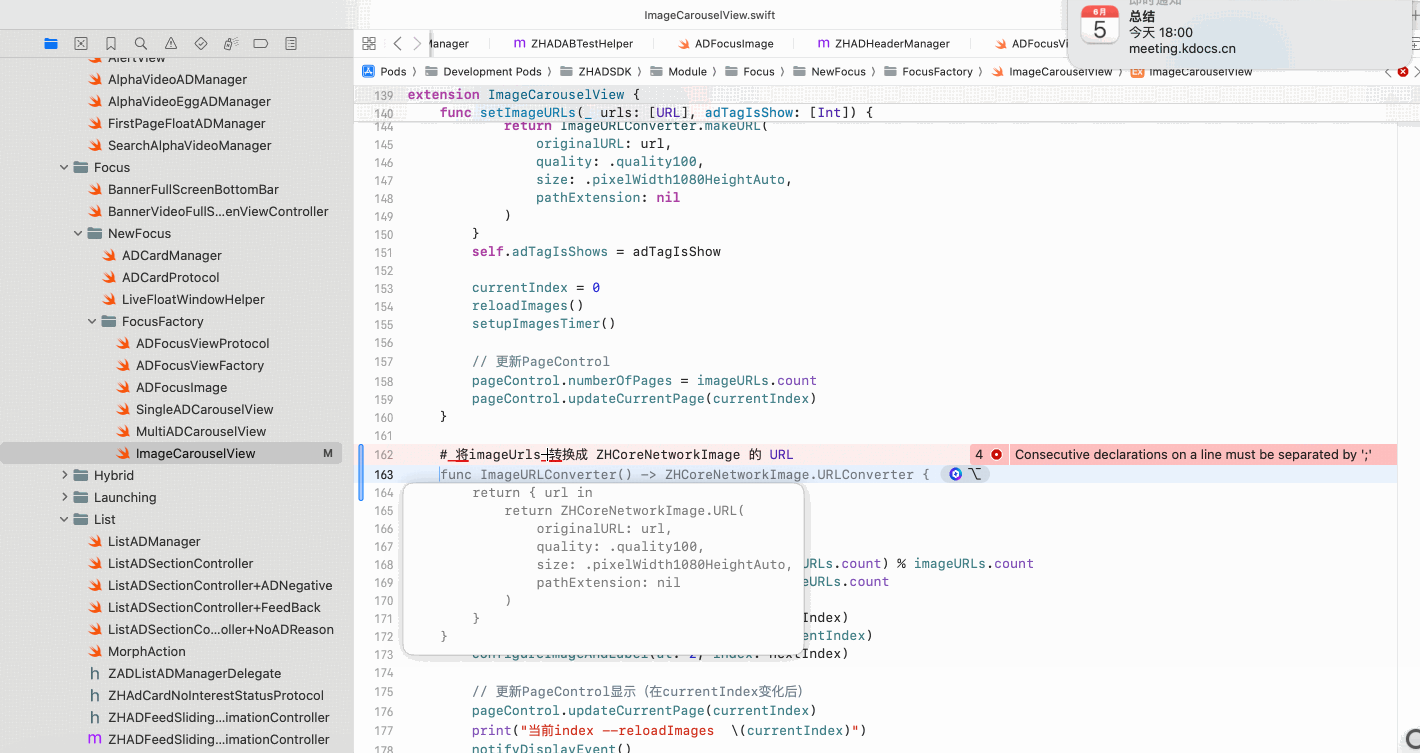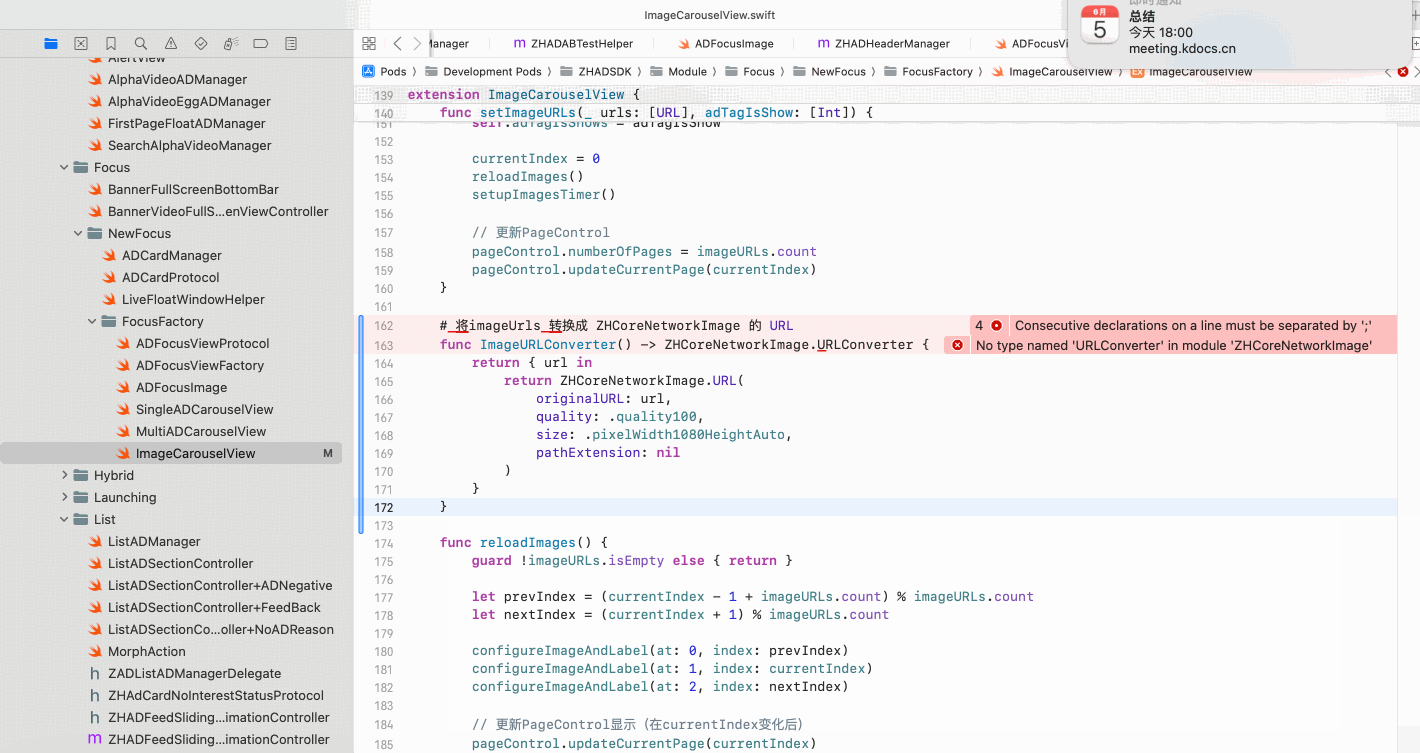
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...
