图论---无向图中国邮路的实现
开始编程前分析设计思路和程序的整体的框架,以及作为数学问题的性质:
程序流程图:
数学原理:
本质上是找到一条欧拉回路,考虑图中的边权重、顶点的度数以及如何通过添加最少的额外边来构造欧拉回路,涉及到欧拉回路、最短路径算法以及奇点匹配。
时间复杂度分析:
程序的时间复杂度主要来自于Floyd算法和ADD函数。Floyd是动态规划算法。它的时间复杂度是O(n^3)。 ADD函数是一个递归函数它的时间复杂度是O(2^n),其中n是奇点的数量。在最坏情况下,奇点的数量可能接近于节点的数量,ADD函数的时间复杂度可能接近于O(2^n)。综合看,这段程序的时间复杂度是O(n^3 + 2^n)。由于2^n的增长速度非常快,当n较大时,2^n将远大于n^3,因此这段程序的时间复杂度应该为O(2^n)
源代码:
#include <stdio.h> #include <bits.h> // 定义常量 const int N = 105; const int inf = 100000000; // 建立矩阵和路径数组 int matrix[N][N], mapp[N][N]; int p[N][N]; int path[N], d[N]; int sg[N]; int cont[N]; int vis[N]; int n, m; int top; // 设置结构体将边和权重关联 struct node {int v, u, cost; } gg[N]; // 使用深度优先递归搜索 void DFS(int beg) {for (int i = 1; i <= n; i++){if (matrix[beg][i]){matrix[beg][i]--;matrix[i][beg]--;DFS(i);}}path[top++] = beg; } void Fleury(int beg) {top = 0;DFS(beg); } // 寻找最短路径 void Floyed() {for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){for (int k = 1; k <= n; k++){if (mapp[i][j] > mapp[i][k] + mapp[k][j]){p[i][j] = k;mapp[i][j] = mapp[i][k] + mapp[k][j];}}}} } // 通过递归对奇数边进行加边 int ADD(int cn) { // 将奇点进行匹配得一个最小的int ans = inf;if (cn < 2)return 0; // 奇点个数小于2,无需匹配。for (int i = 1; i <= cn; i++){if (sg[i] != 0){for (int j = i + 1; j <= cn; j++){if (sg[j] != 0){int tem1 = sg[i], tem2 = sg[j];sg[i] = 0;sg[j] = 0;if (ans > ADD(cn - 2) +mapp[tem1][tem2]){ // 第i个奇点匹配的奇点是第j个奇点cont[i] = tem2; // 第j个奇点匹配的奇点是第i个奇点cont[j] = tem1; ans = ADD(cn - 2)+mapp[tem1][tem2];}sg[i] = tem1;sg[j] = tem2;}}}}return ans; } // 将找到的路径存储 void AddPath(int cn) {memset(vis, 0, sizeof(vis));for (int i = 1; i <= cn; i++){if (!vis[sg[i]]){vis[sg[i]] = 1;vis[cont[i]] = 1;while (p[sg[i]][cont[i]]){int sss = cont[i];cont[i] = p[sg[i]][cont[i]];matrix[sss][cont[i]]++;matrix[cont[i]][sss]++;}matrix[sg[i]][cont[i]]++;matrix[cont[i]][sg[i]]++;}} } // 输出路径 void Print_Path() {printf("top=%d\n", top);for (int i = top - 1; i >= 0; i--){printf("%d", path[i]);if (i)printf("->");}puts(""); } //初始化各边信息 void Inif() {for (int i = 0; i <= N; i++){for (int j = 0; j <= N; j++){mapp[i][j] = (i == j) ? 0 : inf;}} } // 中国邮路信息建立 void CNLoad() {while (~scanf("%d%d", &n, &m)){Inif();int i, beg, sum = 0; // sum用来计算路径长度memset(matrix, 0, sizeof(matrix));memset(d, 0, sizeof(d));memset(sg, 0, sizeof(sg));memset(path, 0, sizeof(path));memset(p, 0, sizeof(p));memset(cont, 0, sizeof(cont));// 存储各边信息for (i = 1; i <= m; i++){int a, b, c;scanf("%d%d%d", &a, &b, &c);d[a]++;d[b]++;matrix[a][b] = 1;matrix[b][a] = 1;mapp[a][b] = c;mapp[b][a] = c;gg[i].v = a;gg[i].u = b;gg[i].cost = c;sum += c;}beg = 1;int cnt = 0;for (i = 1; i <= n; i++){if (d[i] & 1){cnt++;sg[cnt] = i;beg = i;}}if (!cnt){printf("sum=%d\n", sum);Fleury(beg);Print_Path();}else{Floyed();printf("sum=%d\n", sum + ADD(cnt));AddPath(cnt);Fleury(beg);Print_Path();}} } int main() {CNLoad();return 0; }
测试用例:(图结构)
输出结果:
相关文章:

图论---无向图中国邮路的实现
开始编程前分析设计思路和程序的整体的框架,以及作为数学问题的性质: 程序流程图: 数学原理: 本质上是找到一条欧拉回路,考虑图中的边权重、顶点的度数以及如何通过添加最少的额外边来构造欧拉回路,涉及到欧…...

Rockchip RK3588 - Rockchip Linux SDK脚本分析
---------------------------------------------------------------------------------------------------------------------------- 开发板 :ArmSoM-Sige7开发板eMMC :64GBLPDDR4 :8GB 显示屏 :15.6英寸HDMI接口显示屏u-boot &a…...

【C++中resize和reserve的区别】
1. resize的用法 改变当前容器内含有元素的数量(size())比如: vector<int> vct;int num vct.size();//之前的元素个数为num vct.resize(len);//现在的元素个数为len如果num < len ,那么容器vct新增len - num个元素&am…...

计算机毕业设计Python深度学习游戏推荐系统 Django PySpark游戏可视化 游戏数据分析 游戏爬虫 Scrapy 机器学习 人工智能 大数据毕设
本论文的主要研究内容如下: 了解基于Spark的TapTap游戏数据分析系统的基本架构,掌握系统的开发方法,包括系统开发基本流程、开发环境的搭建、测试与运行等。 主要功能如下: (1)用户管理模块:…...

Python面试题:如何在 Python 中进行正则表达式操作?
在 Python 中,正则表达式操作可以通过 re 模块来实现。以下是一些常用的正则表达式操作和示例: 1. 导入模块 import re2. 常见操作和示例 a. 匹配 使用 re.match() 来检查字符串的开头是否匹配某个模式。 pattern r\d # 匹配一个或多个数字 strin…...
?)
C#面:简述什么是中间件(Middleware)?
中间件是组装到应⽤程序管道中以处理请求和响应的软件。 每个组件: 选择是否将请求传递给管道中的下⼀个组件。 可以在调⽤管道中的下⼀个组件之前和之后执⾏⼯作。 请求委托(Request delegates)⽤于构建请求管道,处理每个HTTP请…...

AWS Glue 与 Amazon Redshift 的安全通信配置
1. 引言 在 AWS 环境中,确保服务间的安全通信至关重要。本文将探讨 AWS Glue 与 Amazon Redshift 之间的安全通信配置,特别是为什么需要特定的安全组设置,以及如何正确实施这些配置。 2. 背景 AWS Glue:全托管的 ETL(提取、转换、加载)服务Amazon Redshift:快速、完全…...

nginx访问控制
最近部署consul服务,发现consul认证配置比较麻烦,于是上网查询发现nginx支持路由认证,在此做个记录。 1.Nginx访问控制模块类型 基于IP的访问控制:http_access_module基于用户的信任登录:http_auth_basic_module 2.…...
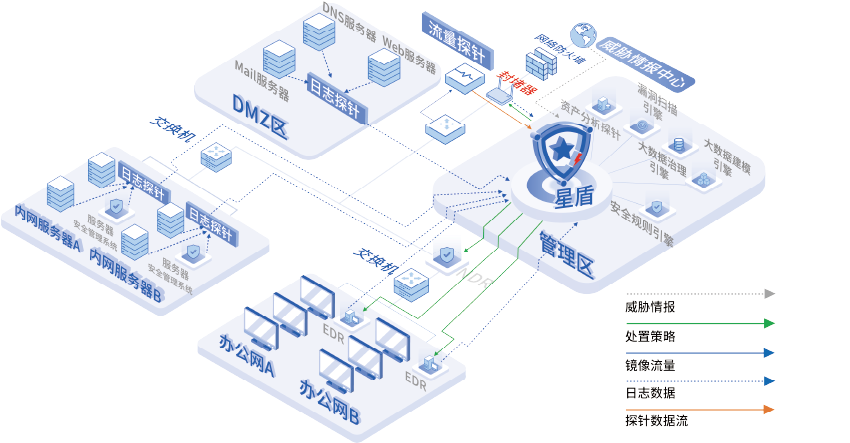
高效应对网络攻击,威胁检测响应(XDR)平台如何提升企业应急响应能力
在数字化时代,企业面临的网络攻击威胁持续增加,如恶意软件、勒索软件、钓鱼攻击、DDoS攻击等。这些威胁不仅危及企业数据安全、系统稳定,还损害了品牌形象和市场信任。随着云计算、大数据、物联网的广泛应用,企业网络攻击面扩大&a…...

多线程问题
什么是线程 线程是cpu调度和执行的单位,一个程序的运行伴随着的是一个进程的执行,而一个进程是由一个或多个线程来完成的,通过cpu调度资源在很短时间切换主线程和子线程并行,交替执行来做到看似多个线程同时进行的状态࿰…...

自动优化:SQL Server数据库自动收缩配置指南
自动优化:SQL Server数据库自动收缩配置指南 在数据库管理中,随着数据的增删,数据库文件的大小会不断变化,导致空间浪费和性能下降。SQL Server提供了自动收缩功能,帮助数据库文件保持最佳状态。本文将深入探讨如何在…...

华为机考真题 -- 密码解密
题目描述: 给定一段"密文"字符串 s, 其中字符都是经过"密码本"映射的,现需要将"密文"解密并且输出映射的规则 (a - i)分别用(1 - 9)表示;(j - z)分别用(10* - 26*)表示约束:映射始终唯…...

ScrapySharp框架:小红书视频数据采集的API集成与应用
引言 随着大数据时代的到来,数据采集成为了互联网企业获取信息的重要手段。小红书作为一个集社交和电商于一体的平台,其丰富的用户生成内容(UGC)为数据采集提供了丰富的资源。本文将介绍如何使用ScrapySharp框架进行小红书视频数…...

PostgreSQL 数据库监控项
在维护和优化 PostgreSQL 数据库时,采集并监控数据库的各种静态和动态指标非常重要。这些指标包括数据库的配置信息、资源使用情况、性能指标等,能够帮助数据库管理员及时发现并解决潜在的问题,从而提高数据库的稳定性和性能。本文提供了一系…...

用python生成词频云图(python实例二十一)
目录 1.认识Python 2.环境与工具 2.1 python环境 2.2 Visual Studio Code编译 3.词频云图 3.1 代码构思 3.2 代码实例 3.3 运行结果 4.总结 1.认识Python Python 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。 Python 的设计具有很强的可读性&a…...

HTML 标签简写和全称及其对应的中文说明和实例
<!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>HTML 标签简写及全称</title><style>…...
docker-compose实战 (9)部署多项目环境(LAMP+react+vue+redis+mysql+nginx))
(2024)docker-compose实战 (9)部署多项目环境(LAMP+react+vue+redis+mysql+nginx)
前言 本系列最初的想法就是搭建一个多项目的环境, 包含nginx, nodejs, php, html, redis, MongoDB, mysql.本文使用的PHP镜像为php:7.3.6-apache, 这里可以使用上一篇文章中生成好的镜像.LAMP或包含react或vue的前端项目, 本文就各写了一个, 可以按照实际需求, 自行添加多个容…...

全网最适合入门的面向对象编程教程:13 类和对象的 Python 实现-可视化阅读代码神器 Sourcetrail 的安装使用
全网最适合入门的面向对象编程教程:13 类和对象的 Python 实现-可视化阅读代码神器 Sourcetrail 的安装使用 摘要: 本文主要介绍了可视化阅读代码神器Sourcetrail的安装与使用,包括软件简介和特性、下载地址、安装方式、新建工程和如何查看…...

Django 视图 - FBV 与 CBV
Django 视图 - FBV 与 CBV 在 Django 框架中,视图是处理 Web 请求和返回 Web 响应的核心组件。Django 提供了两种主要的视图编写方式:函数基础视图(Function-Based Views,简称 FBV)和类基础视图(Class-Bas…...

AI机器人在未来的应用场景预测:是否会取代人类?华为、百度、特斯拉他们在AI领域都在做什么?
引言 随着人工智能(AI)技术的飞速发展,AI机器人在各个领域的应用变得越来越普遍。从工业自动化到日常生活,AI机器人已经开始展现出强大的潜力和实际应用价值。本文将深入探讨AI机器人在未来的应用场景,并分析它们是否…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...




