第1节 线性回归模型
1. 模型概述
对于收集到的数据(xi,yi)(x_i,y_i)(xi,yi),建立线性回归模型yi=θTxi+εi(1)y_i=\theta^{^T} x_i +\varepsilon_i (1)yi=θTxi+εi(1)
需要估计的参数为θT\theta^{^T}θT,我们的目的是让估计的参数θT\theta^{^T}θT和xix_ixi组合后,得到的估计值y^i\hat{y}_iy^i与实际值yiy_iyi越接近越好,也就是随机误差项εi\varepsilon_iεi越小越好。
2. 模型求解
由于假设模型的误差项是服从独立同分布(独立:数据之间互相不影响,同分布:保证模型使用于某一类数据)的高斯分布(标准正态分布)1,即ϵ∼N(0,σ2)\epsilon \sim N(0, \sigma^2)ϵ∼N(0,σ2),则其概率密度函数为
p(ϵi)=12πσexp(−εi22σ2)(2)p(\epsilon_i)=\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{\varepsilon_i^2}{2\sigma^2})(2)p(ϵi)=2πσ1exp(−2σ2εi2)(2)
对(1)式进行变形,则有εi=yi−θTxi\varepsilon_i=y_i-\theta^{^T} x_iεi=yi−θTxi,将其带入(2)式,得
p(yi∣xi,θ)=12πσexp(−(yi−θTxi)22σ2)p(y_i|x_i,\theta)=\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\theta^{^T} x_i)^2}{2\sigma^2})p(yi∣xi,θ)=2πσ1exp(−2σ2(yi−θTxi)2)
因为我们的目的是让求解得出的参数θ\thetaθ和和xix_ixi组合后,得到的估计值y^i=θTxi\hat{y}_i=\theta^{^T} x_iy^i=θTxi是真实值yiy_iyi的概率越大越好,也就是让这个概率越大越好。
由于以上只是单个的样本数据,假设我们有mmm个样本数据,样本之间互相独立,则所有的样本的概率等于单个样本的概率的乘积,我们将所有样本的概率记为似然函数L(θ)L(\theta)L(θ),则
L(θ)=∏i=0m12πσexp(−(yi−θTxi)22σ2)L(\theta)=\prod \limits_{i=0}^m\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\theta^{^T} x_i)^2}{2\sigma^2})L(θ)=i=0∏m2πσ1exp(−2σ2(yi−θTxi)2)
由于多个式子相乘难以求解,我们可利用对数将其转化为加法。两边同时取对数,得到对数似然函数lnL(θ)lnL(\theta)lnL(θ),
lnL(θ)=ln∏i=0m12πσexp(−(yi−θTxi)22σ2)lnL(\theta)=ln\prod \limits_{i=0}^m\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\theta^{^T} x_i)^2}{2\sigma^2})lnL(θ)=lni=0∏m2πσ1exp(−2σ2(yi−θTxi)2)
即
lnL(θ)=mln12πσ−1σ212∑i=1m(yi−θTxi)2lnL(\theta)=mln\frac{1}{\sqrt{2\pi}\sigma }-\frac{1}{\sigma^2}\frac{1}{2}\sum_{i=1}^m(y_i-\theta^{^T} x_i)^2lnL(θ)=mln2πσ1−σ2121i=1∑m(yi−θTxi)2
要对上述式子求最大值,则相当于对12∑i=1m(yi−θTxi)2\frac{1}{2}\sum_{i=1}^m(y_i-\theta^{^T} x_i)^221∑i=1m(yi−θTxi)2求最小值,我们将其记为J(θ)J(\theta)J(θ),并取名为目标函数,则目标函数为
J(θ)=12∑i=1m(yi−θTxi)2J(\theta)=\frac{1}{2}\sum_{i=1}^m(y_i-\theta^{^T} x_i)^2J(θ)=21i=1∑m(yi−θTxi)2
那么,求解这个目标函数所使用的方法就是最小二乘法,最小二乘法的代数法解法就是对θi\theta_iθi求偏导数,令偏导数为0,再解方程组,得到θi\theta_iθi的估计值。矩阵法比代数法要简洁,下面主要讲解下矩阵法解法。
由于
J(θ)=12∑i=1m(yi−θTxi)2=12∑i=1m(θTxi−yi)2=12(Xθ−Y)T(Xθ−Y)J(\theta)=\frac{1}{2}\sum_{i=1}^m(y_i-\theta^{^T} x_i)^2=\frac{1}{2}\sum_{i=1}^m(\theta^{^T} x_i-y_i)^2=\frac{1}{2}(X\theta-Y)^{^T}(X\theta-Y)J(θ)=21i=1∑m(yi−θTxi)2=21i=1∑m(θTxi−yi)2=21(Xθ−Y)T(Xθ−Y)
我们需要对其求偏导,∂J(θ)∂θ=12∂(θTXTXθ−θTXTY−YTXθ+YTY)∂θ=12(2XTXθ−2XTY)\frac{\partial J(\theta)}{\partial \theta}=\frac{1}{2}\frac{\partial (\theta^{^T}X^{^T}X\theta-\theta^{^T}X^{^T}Y-Y^{^T}X\theta+Y^{^T}Y)}{\partial \theta}=\frac{1}{2}(2X^{^T}X\theta-2X^{^T}Y)∂θ∂J(θ)=21∂θ∂(θTXTXθ−θTXTY−YTXθ+YTY)=21(2XTXθ−2XTY),令其等于0,得θ^=(XTX)−1XTY\hat \theta=( X^{^T}X)^{-1}X^{^T}Yθ^=(XTX)−1XTY
这里,需要用到矩阵求导的公式2.
在了解正态分布之前,我们需要先了解一个概念——概率分布。概率分布是指:经过大量的重复试验,将随机事件的所有可能的出现结果的次数分布记录下来,并在坐标系中做出一条曲线,这条曲线就是数据的概率分布曲线,由概率分布曲线可以估算变量的概率。正态分布就是一种常见的概率分布,它的概率分布曲线是一个钟形曲线,生活中大量的变量都服从正态分布,例如:人群的身高、鞋码、学生成绩等。正态分布只依赖于数据的两个特征:均值和方差。标准正态分布的均值为0,方差为σ2\sigma^2σ2. ↩︎
∂XTA∂A=∂ATX∂X=A,∂XTAX∂X=AX+ATX\frac{\partial X^{^T} A }{\partial A}=\frac{\partial A^{^T} X }{\partial X}=A, \frac{\partial X^{^T} A X}{\partial X}=AX+ A^{^T} X∂A∂XTA=∂X∂ATX=A,∂X∂XTAX=AX+ATX ↩︎
相关文章:

第1节 线性回归模型
1. 模型概述 对于收集到的数据(xi,yi)(x_i,y_i)(xi,yi),建立线性回归模型yiθTxiεi(1)y_i\theta^{^T} x_i \varepsilon_i (1)yiθTxiεi(1) 需要估计的参数为θT\theta^{^T}θT,我们的目的是让估计的参数θT\theta^{^T}θT和xix_ixi…...
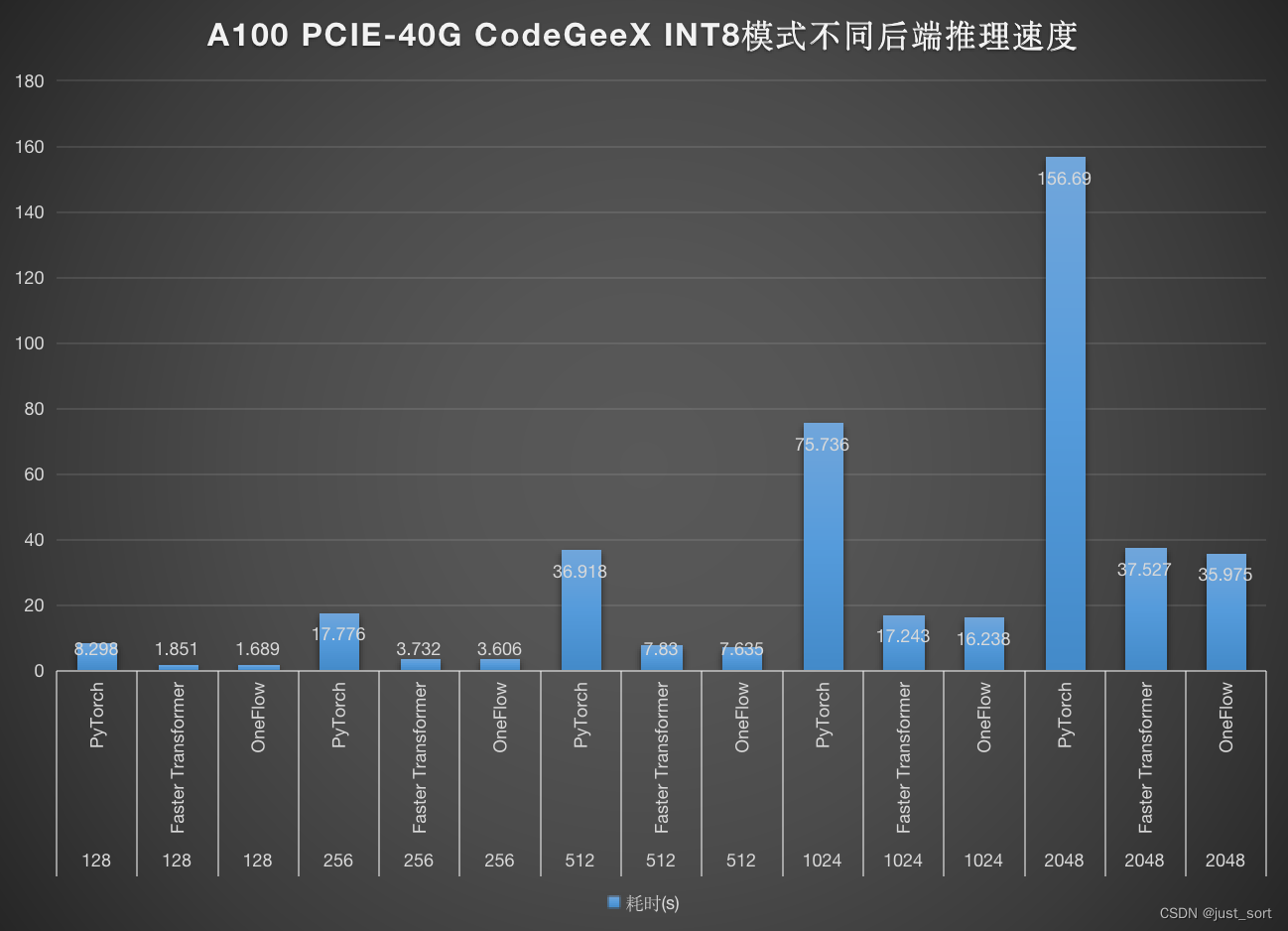
CodeGeeX 130亿参数大模型的调优笔记:比FasterTransformer更快的解决方案
0x0 背景 相信大家都使用或者听说过github copilot这个高效的代码生成工具。CodeGeeX类似于github copilot,是由清华大学,北京智源研究院,智谱AI等机构共同开发的一个拥有130亿参数的多编程语言代码生成预训练模型。它在vscode上也提供了插件…...

Linux驱动之并发与竞争
文章目录并发与竞争的概念原子操作原子整形操作 API 函数原子位操作 API 函数自旋锁自旋锁简介自旋锁结构体自旋锁 API 函数自旋锁的注意事项读写自旋锁读写自旋锁的API顺序锁顺序锁的APIRCU(Read-Copy-Update)RCU的API信号量信号量API互斥体互斥体的API完成量(Completion)完成…...

【密码学复习】第四讲分组密码(三)
AES算法的整体结构 AES算法的轮函数 1)字节代换(SubByte) 2)行移位(ShiftRow) 3)列混合(MixColumn) 4)密钥加(AddRoundKey)1-字节代换…...

JVM(内存划分,类加载,垃圾回收)
JVMJava程序,是一个名字为Java 的进程,这个进程就是所说的“JVM”1.内存区域划分JVM会先从操作系统这里申请一块内存空间,在这个基础上再把这个内存空间划分为几个小的区域在一个JVM进程中,堆和方法区只有一份;栈和程序…...

工作中遇到的问题 -- 你见过哪些写的特别好的代码
strPtr : uintptr((*(*stringStruct)(unsafe.Pointer(&str))).str)代码解析: 这是一段 Go 代码,它的作用是获取一个字符串变量 str 的底层指针,即字符串数据的起始地址。 这段代码涉及到了 Go 语言中的指针、类型转换和内存布局等概念&…...

基于chatGPT设计卷积神经网络
1. 简介 本文主要介绍基于chatGPT,设计一个针对骁龙855芯片设计的友好型神经网络。 提问->跑通总共花了5min左右,最终得到的网络在Cifar100数据集上与ResNet18的精度对比如下。 模型flopsparamstrain acc1/5test acc1/5ResNet18(timm)1.8211.18~98…...

java.sql.Date和java.util.Date的区别
参考答案 java.sql.Date 是 java.util.Date 的子类java.util.Date 是 JDK 中的日期类,精确到时、分、秒、毫秒java.sql.Date 与数据库 Date 相对应的一个类型,只有日期部分,时分秒都会设置为 0,如:2019-10-23 00:00:0…...
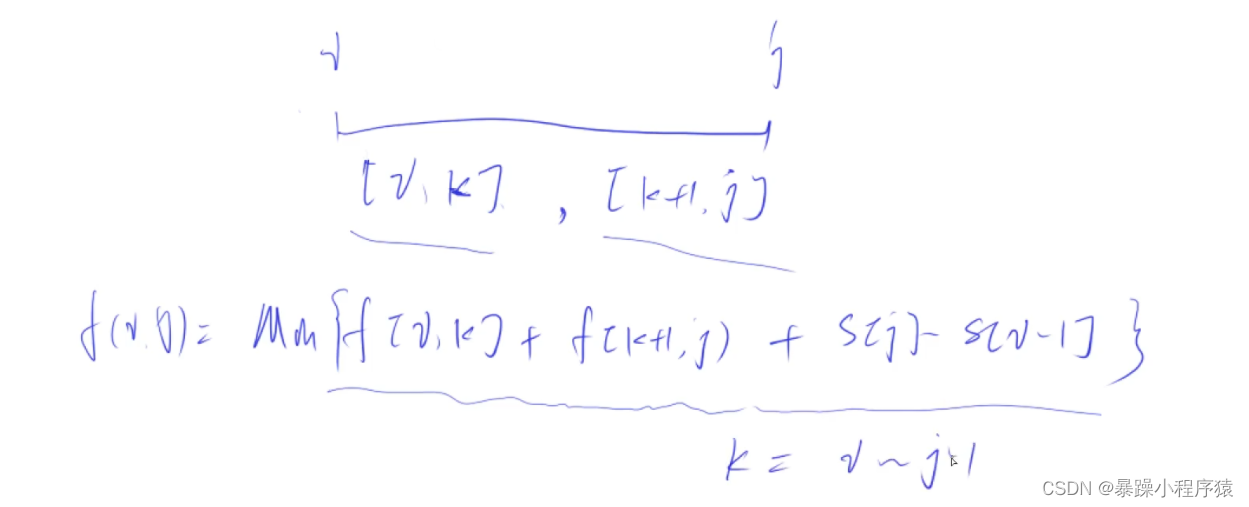
动态规划---线性dp和区间dp
动态规划(三) 目录动态规划(三)一:线性DP1.数字三角形1.1数字三角形题目1.2代码思路1.3代码实现(正序and倒序)2.最长上升子序列2.1最长上升子序列题目2.2代码思路2.3代码实现3.最长公共子序列3.1最长公共子序列题目3.2代码思路3.3代码实现4.石子合并4.1题目如下4.2代…...

常见的2D与3D碰撞检测算法
分离轴分离轴定理(Separating Axis Theorem)是用于解决2D或3D物体碰撞检测问题的一种方法。其基本思想是,如果两个物体未发生碰撞,那么可以找到一条分离轴(即一条直线或平面),两个物体在该轴上的…...

STM32 10个工程篇:1.IAP远程升级(二)
一直提醒自己要更新CSDN博客,但是确实这段时间到了一个项目的关键节点,杂七杂八的事情突然就一涌而至。STM32、FPGA下位机代码和对应Labview的IAP升级助手、波形设置助手上位机代码笔者已经调试通过,因为不想去水博客、凑数量,复制…...
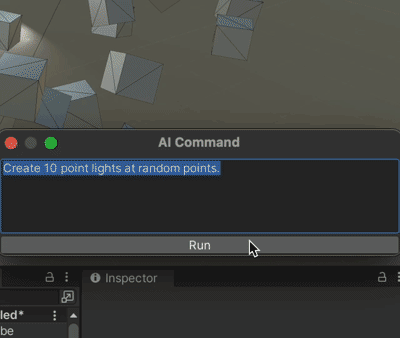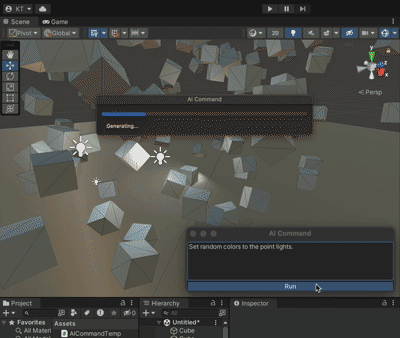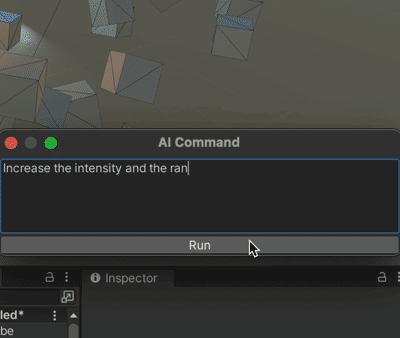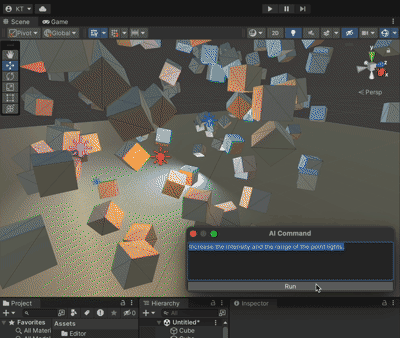
Unity+ChatGpt的联动 AICommand
果然爱是会消失的,对吗 chatGpt没出现之前起码还看人家的文章,现在都是随便你。 本着师夷长技以制夷的思路,既然打不过,那么我就加入 github地址:https://github.com/keijiro/AICommand 文档用chatGpt翻译如下&#…...
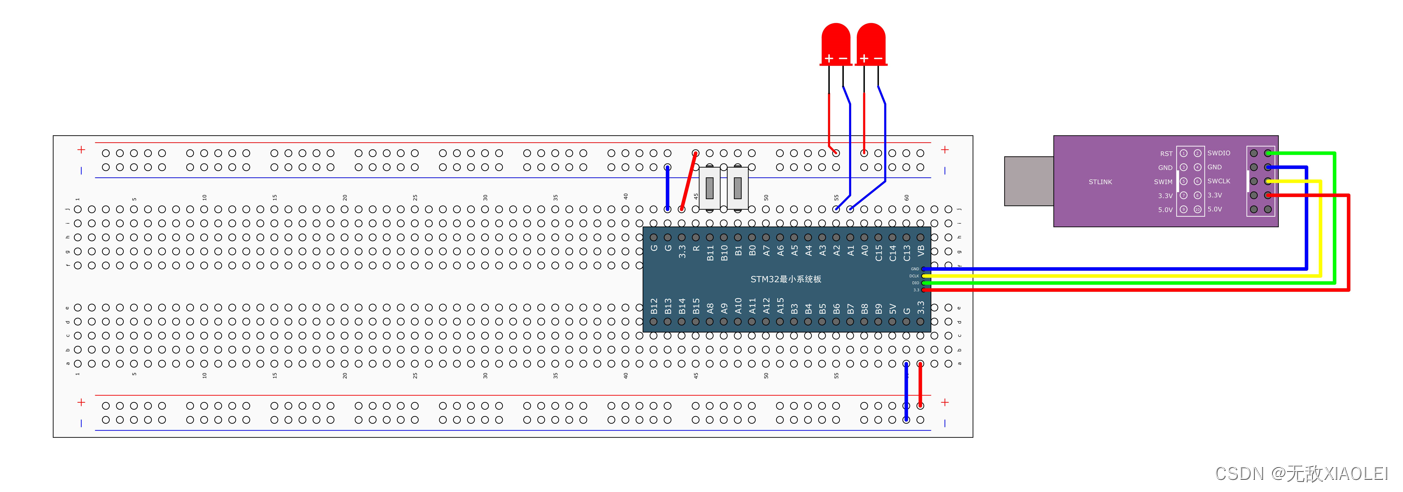
STM-32:按键控制LED灯 程序详解
目录一、基本原理二、接线图三、程序思路3.1库函数3.2程序代码注:一、基本原理 左边是STM322里电路每一个端口均可以配置的电路部分,右边部分是外接设备 电路图。 配置为 上拉输入模式的意思就是,VDD开关闭合,VSS开关断开。 浮空…...
北邮22信通:(8)实验1 题目五:大整数加减法(搬运官方代码)
北邮22信通一枚~ 跟随课程进度每周更新数据结构与算法的代码和文章 持续关注作者 解锁更多邮苑信通专属代码~ 上一篇文章: 北邮22信通:(7)实验1 题目四:一元多项式(节省内存版)_青山如…...

Fiddler抓取https史上最强教程
有任何疑问建议观看下面视频 2023最新Fiddler抓包工具实战,2小时精通十年技术!!!对于想抓取HTTPS的测试初学者来说,常用的工具就是fiddler。 但是初学时,大家对于fiddler如何抓取HTTPS难免走歪路ÿ…...
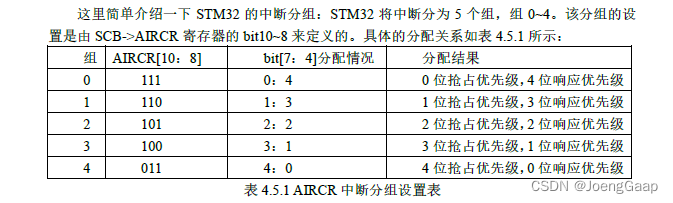
STM32开发基础知识入门
C语言基础 位操作 对基本类型变量可以在位级别进行操作。 1) 不改变其他位的值的状况下,对某几个位进行设值。 先对需要设置的位用&操作符进行清零操作,然后用|操作符设值。 2) 移位操作提高代码的可读性。 3) ~取反操作使用技巧 可用于对某…...

学习操作系统的必备教科书《操作系统:原理与实现》| 文末赠书4本
使用了6年的实时操作系统,是时候梳理一下它的知识点了 摘要: 本文简单介绍了博主学习操作系统的心路历程,同时还给大家总结了一下当下流行的几种实时操作系统,以及在工程中OSAL应该如何设计。希望对大家有所启发和帮助。 文章目录…...
)
大数据的常用算法(分类、回归分析、聚类、关联规则、神经网络方法、web数据挖掘)
在大数据时代,数据挖掘是最关键的工作。大数据的挖掘是从海量、不完全的、有噪声的、模糊的、随机的大型数据库中发现隐含在其中有价值的、潜在有用的信息和知识的过程,也是一种决策支持过程。其主要基于人工智能,机器学习,模式学…...
【数据结构】详解二叉树与堆与堆排序的关系
🌇个人主页:平凡的小苏 📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情 🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html 🚀数据结构专栏ÿ…...
【Pandas】数据分析入门
文章目录前言一、Pandas简介1.1 什么是Pandas1.2 Pandas应用二、Series结构2.1 Series简介2.2 基本使用三、DataFrame结构3.1 DataFrame简介3.2 基本使用四、Pandas-CSV4.1 CSV简介4.2 读取CSV文件4.3 数据处理五、数据清洗5.1 数据清洗的方法5.2 清洗案例总结前言 大家好&…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
