[C++][数据结构][哈希表]详细讲解
目录
1. 哈希概念
2.哈希冲突
3.哈希函数
4.哈希冲突解决
4.1闭散列
4.1.1何时扩容?如何扩容?
4.1.2线性探测
4.1.3二次探测
4.2开散列(哈希桶)
4.2.1概念
4.2.2开散列增容
1. 哈希概念
- 顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素时,必须要经过关键码的多次比较。顺序查找时间复杂度为O(N),平衡树中为树的高度,即 O(logN),搜索的效率取决于搜索过程中元素的比较次数
- 理想的搜索方法:可以不经过任何比较,一次直接从表中得到要搜索的元素
- 如果构造一种存储结构,通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素
- 当向该结构中:
1.插入元素
根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放
2.搜索元素
对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置取元素比较,若关键 码相等,则搜索成功
3.该方式即为哈希(散列)方法,哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表(Hash Table) (或者称散列表)
2.哈希冲突
对于两个数据元素的关键字k_i和k_j(i != j),有k_i != k_j,但有:Hash(k_i) == Hash(k_j)
- 即:不同关键字通过相同哈希函数计算出相同的哈希地址,该种现象称为 哈希冲突 或 哈希碰撞
- 把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”
3.哈希函数
引起哈希冲突的一个原因可能是:哈希函数设计不够合理
哈希函数设计原则:
- 哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到m-1之间
- 哈希函数计算出来的地址能均匀分布在整个空间中
- 哈希函数应该比较简单
常见哈希函数:
1.直接定址法 – (常用) --> 不存在哈希冲突
- 取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B
- 优点:简单、均匀
- 缺点:需要事先知道关键字的分布情况
- 使用场景:适合查找比较小且连续的情况
2.除留余数法 – (常用) --> 存在哈希冲突,重点解决哈希冲突
- 设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数
- 按照哈希函数:Hash(key) = key% p (p<=m),将关键码转换成哈希地址
3.平方取中法 – (了解)
- 假设关键字为1234,对它平方就是1522756,抽取中间的3位227作为哈希地址;
- 再比如关键字为4321,对它平方就是18671041,抽取中间的3位671(或710)作为哈希地址
- 平方取中法比较适合:不知道关键字的分布,而位数又不是很大的情况
4.折叠法 – (了解)
- 折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些),然后将这几部分叠加求和,并按散列表表长,取后几位作为散列地址
- 折叠法适合事先不需要知道关键字的分布,适合关键字位数比较多的情况
5.随机数法 – (了解)
- 选择一个随机函数,取关键字的随机函数值为它的哈希地址
- 即H(key) = random(key),其中 random为随机数函数
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突
4.哈希冲突解决
解决哈希冲突两种常见的方法是:闭散列和开散列
4.1闭散列
闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置呢?
4.1.1何时扩容?如何扩容?
1.散列表的载荷因子定义为:α = 填入表中的元素个数 / 散列表的长度
- α越大,表中元素越多,产生冲突概率越大
- α越小,表明元素越少,产生冲突概率越小
- 一般不要超过0.7~0.8
2.什么时候扩容? --> 负载因子到一个基准值就扩容
- 基准值越大,冲突越多,效率越低,空间利用率越高
- 基准值越小,冲突越少,效率越高,空间利用率越低
4.1.2线性探测
线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止
1.插入
-
通过哈希函数获取待插入元素在哈希表中的位置
-
如果该位置中没有元素则直接插入新元素
-
如果该位置中有元素发生哈希冲突, 使用线性探测找到下一个空位置,插入新元素

2.删除
- 采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素,会影响其他元素的搜索
- 比如删除元素4,如果直接删除掉,44查找起来可能会受影响
- 因此线性探测采用标记的伪删除法来删除一个元素
4.1.3二次探测
1.线性探测的缺陷是产生冲突的数据堆积在一块,这与其找下一个空位置有关系,因为找空位置的方式就是挨着往后逐个去找
2.因此二次探测为了避免该问题,找下一个空位置的方法为:
- H_i = (H_0 + i^2 ) % m 或者 H_i = (H_0 - i^2 ) % m (i = 1,2,3**…)**
- H_0是通过散列函数Hash(x)对元素的关键码 key 进行计算得到的位置,m是表的大小
3.研究表明:
- 当表的长度为质数且表载荷因子a不超过0.5时,新的表项一定能够插入,而且任何一个位置都不会被探查两次
- 因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装满的情况,但在插入时必须确保表的装载因子a不超过0.5,如果超出必须考虑增容
因此:闭散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷
namespace CH1
{enum STATE{EXIST,EMPTY,DELETE};template<class K>struct DefaultHashFunc{size_t operator()(const K& key){return (size_t)key;}};template<>//特化struct DefaultHashFunc<string>{size_t operator()(const string& str){int sum = 0;for (auto& x : str){sum *= 131;sum += x;}return sum;}};template<class K, class V>struct HashDate{pair<K, V> _kv;STATE _state = EMPTY;};template<class K, class V, class HashFunc = DefaultHashFunc<K>>class HashTable{public://构造函数HashTable(){_table.resize(10);}//插入bool insert(const pair<K, V>& kv){//负载因子到了就扩容if ((double)n / _table.size() >= 0.7){size_t newsize = _table.size() * 2;HashTable<K, V> newtable;//开创一个新表,将原来的数据,都移过来,并且重新赋予位置newtable._table.resize(newsize);//将原来的数据移过来for (size_t i = 0; i < _table.size(); i++){if (_table[i]._state == EXIST){newtable.insert(_table[i]._kv);}}//两表交换,新创建的表,出了作用域会被销毁_table.swap(newtable._table);}HashFunc hf;// 哈希地址计算size_t hashnum = hf(kv.first) % _table.size();while (_table[hashnum]._state == EXIST)//找到空{hashnum += 1;hashnum %= _table.size();}_table[hashnum]._kv = kv;_table[hashnum]._state = EXIST;++n;return true;}HashDate<const K, V>* Find(const K& key){HashFunc hf;size_t hashi = hf(key) % _table.size();while (_table[hashi]._state != EMPTY){if (_table[hashi]._state == EXIST && _table[hashi]._kv.first == key){return (HashDate<const K, V>*) & _table[hashi];}hashi++;hashi %= _table.size();}return nullptr;}bool erase(const K& key){HashDate<K, V>* ret = Find(key);if (ret){ret->_state = DELETE;n--;}else{return false;}}void printf(){for (size_t i = 0; i < _table.size(); i++){cout << _table[i]._kv.first << " ";}}private:vector<HashDate<K, V>> _table;size_t n = 0;//记录数据有效数据};
}4.2开散列(哈希桶)
4.2.1概念
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中

从上图可以看出,开散列中每个桶中放的都是发生哈希冲突的元素
4.2.2开散列增容
- 桶的个数是一定的,随着元素的不断插入,每个桶中元素的个数不断增多,极端情况下,可能会导致一个桶中链表节点非常多,会影响的哈希表的性能,因此在一定条件下需要对哈希表进行增容,那该条件怎么确认呢?
- 开散列最好的情况是:每个哈希桶中刚好挂一个节点, 再继续插入元素时,每一次都会发生哈希冲突,因此,在元素个数刚好等于桶的个数时,可以给哈希表增容
4.2.3开散列思考
-
只能存储key为整形的元素,其他类型怎么解决?
-
哈希函数采用处理余数法,被模的key必须要为整形才可以处理,此处提供将key转化为整形的方法::利用仿函数
-
除留余数法,最好模一个素数,如何每次快速取一个类似两倍关系的素数?‘
4.2.4开散列与闭散列比较
应用链地址法处理溢出,需要增设链接指针,似乎增加了存储开销
事实上:
- 由于开放定址法必须保持大量的空闲空间以确保搜索效率,如二次探查法要求装载因子a <= 0.7
- 而表项所占空间又比指针大的多,所以使用链地址法反而比开地址法节省存储空间
namespace CH2
{template<class K>struct DefaultHashFunc{size_t operator()(const K& key){return (size_t)key;}};template<>struct DefaultHashFunc<string>{size_t operator()(const string& str){int sum = 0;for (auto& x : str){sum *= 131;sum += x;}return sum;}};template<class K,class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K,V>& kv):_kv(kv),_next(nullptr){}};template<class K, class V, class HashFunc= DefaultHashFunc<K>>class HashTable{typedef HashNode<K, V> Node;public:HashTable(){_table.resize(10, nullptr);}~HashTable(){for (size_t i = 0; i < _table.size(); i++){Node* cur = _table[i];//释放每一个节点while (cur){Node* next = cur->_next;delete cur;cur = next;}_table[i] = nullptr;}}bool insert(const pair<K,V>& kv){HashFunc ht;//扩容if (_n == _table.size()){size_t newhashi = 2 * _table.size();vector<Node*> newtable;newtable.resize(newhashi,nullptr);for (size_t i = 0; i < _table.size(); i++){Node* cur = _table[i];while (cur){Node* next = cur->_next;size_t hashi = ht(cur->_kv.first) % newtable.size();cur->_next = newtable[hashi];newtable[hashi] = cur;cur = next;}_table[i] = nullptr;}_table.swap(newtable);}size_t hashi = ht(kv.first) % _table.size();Node* cur = new Node(kv);cur->_next = _table[hashi];_table[hashi] = cur;_n++;return true;}Node* Find(const K& key){HashFunc ht;size_t hashi = ht(key) % _table.size();Node* cur = _table[hashi];while (cur){Node* next = cur->_next;if (cur->_kv.first == key){return cur;}cur = next;}return nullptr;}bool erase(const K& key){HashFunc ht;size_t hashi = ht(key) % _table.size();Node* cur = _table[hashi];Node* prve = nullptr;while (cur){//头删//中间删if (ht(cur->_kv.first) == key){if (prve == nullptr){_table[hashi] = cur->_next;}else{prve->_next = cur->_next;}delete cur;return true;}prve = cur;cur = cur->_next;}return false;}void print(){for (size_t i = 0; i < _table.size(); i++){Node* cur = _table[i];printf("%zd->", i);while (cur){cout << cur->_kv.first << "->";cur = cur->_next;}cout << "Null" << endl;}}private:vector<Node*> _table;//创建一个数组,数组中的每一个成员都是节点size_t _n = 0;//记录有效个数};
}相关文章:

[C++][数据结构][哈希表]详细讲解
目录 1. 哈希概念 2.哈希冲突 3.哈希函数 4.哈希冲突解决 4.1闭散列 4.1.1何时扩容?如何扩容? 4.1.2线性探测 4.1.3二次探测 4.2开散列(哈希桶) 4.2.1概念 4.2.2开散列增容 1. 哈希概念 顺序结构以及平衡树中,元素关键码与其存储…...

Android Gradle
#1024程序员节|征文# Gradle 是一款强大的自动化构建工具,广泛应用于 Android 应用开发。它通过灵活的配置和丰富的插件系统,为项目构建提供了极大的便利。本文只是简单的介绍 Gradle 在 Android 开发中的使用,包括其核心概念、构…...

Vue2自定义指令及插槽
这里写目录标题 自定义指令基础语法指令的值封装v-loading指令 插槽默认插槽后备内容(插槽的默认值)具名插槽作用域插槽 自定义指令 自定义指令:自己定义的指令,封装一些dom操作,扩展额外功能 基础语法 全局注册&am…...

【Qt】系统相关——多线程、Qt多线程介绍、常用函数、线程安全、网络、UDP Socket、TCP Socket
文章目录 Qt系统相关1. 多线程1.1 Qt多线程介绍1.2 常用函数1.3 线程安全 2. 网络2.1 UDP Socket2.2 TCP Socket Qt 系统相关 1. 多线程 1.1 Qt多线程介绍 QThread 代表一个在应用程序中可以独立控制的线程,它还可以和进程中的其他线程共享数据。QThread 对象管理…...

1GS/s 4通道14bit PCIE采集卡
1GS/s 4通道14bit PCIE采集卡是一款同时具备直流耦合程控放大器和双极性宽带信号输入的高速数据采集卡。板载FPGA具备实时信号处理能力,这些特性使其成为激光雷达、光纤传感、粒子物理等应用领域进行信号采集和分析的理想工具。提供快速的PCI Express 3.0 x8数据传输…...

动态IP是什么?
随着互联网成为人们生活的重要组成部分,以信息传递为主导的时代种,网络连接质量对我们的工作效率、学习进度以及娱乐体验等方面都有很大影响。 动态IP,作为网络连接中的一种重要IP代理形式,越来越受到用户的欢迎。本文将深入解析…...

51单片机完全学习——红外遥控
一、红外接收模块原理 红外接收头内部本身有一个反相,意思就是:平时发送方无信号时接收到的是1,发送方有发送载波时接收头引脚输出的是0,写代码的时候注意这一点。红外协议,你也可以理解成,他对0和1重新做…...

群控系统服务端开发模式-应用开发-业务架构逻辑开发BaseAPI
一、加密工具开发 首先在根目录下extend文件中创建Encipher文件夹,用于专门开发加解密工具,新建RSA算法控制器并命名为Encrypt.php。然后在根目录下config文件夹中创建rsa.php文件,用于配置RSA算法参数。 1、秘钥生成算法 <?php /*** RS…...

【AI日记】24.10.27 了解AI的未来
【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】【AI日记】 工作 工作1 内容:挑选AI大佬的访谈,跳着看了几个时间:2小时 工作2 内容:OpenAI Sam Altman最新访谈:GPT-4o和AI未来 2024.5时间:2小时收…...

【时间之外】IT人求职和创业应知【19】
认知决定你的赚钱能力。以下是今天可能影响你求职和创业的热点新闻: 今日关键字:深圳长沙(备注:我都没有去过) 2024中国(长沙)民营企业科技创新发展大会召开 内容概述: 2024年10月…...

MOE混合专家模型总结(面试)
目录 1. MOE介绍 2.MOE出现的背景 3.有哪些MOE模型 4.门控网络或路由 5.为什么门控网络要引入噪声 6.如何均衡专家间的负载 7.“专家”指什么 8.专家的数量对预训练有何影响 9.什么是topk门控 10.MOE模型的主要特点 11.MOE和稠密模型的对比 12.MOE的优势 13.MOE的挑…...

第8次CCF CSP认证真题解
1、最大波动 题目链接:https://sim.csp.thusaac.com/contest/8/problem/0 100分代码: #include <iostream> #include <algorithm> using namespace std; int main(int argc, char *argv[]) {int n;cin >> n;int a[1010];for(int i …...
)
2024昆明ICPC A. Two-star Contest(直观命名+详细注释)
Problem - A - Codeforces 思路: 按照等级排序,维护同等级最大评分,每个等级的总评分至少比其第前一个等级的最大评分大1分 吐槽: 思路不难,但坑好多,感觉全踩了一遍 坑:(按解决…...

【算法刷题指南】双指针
🌈个人主页: 南桥几晴秋 🌈C专栏: 南桥谈C 🌈C语言专栏: C语言学习系列 🌈Linux学习专栏: 南桥谈Linux 🌈数据结构学习专栏: 数据结构杂谈 🌈数据…...
HTML,CSS,JavaScript三件套
前言 1.HTML 就是用来写网页的 就是超文本标记语言 1.1快速入门 标签是根标签,就是开始的地方 head就是头,加载一些资源信息,和展示title标题的地方,比如html快速入门那几个字就是title标题标签 body是身体,就是正…...
react 总结+复习+应用加深
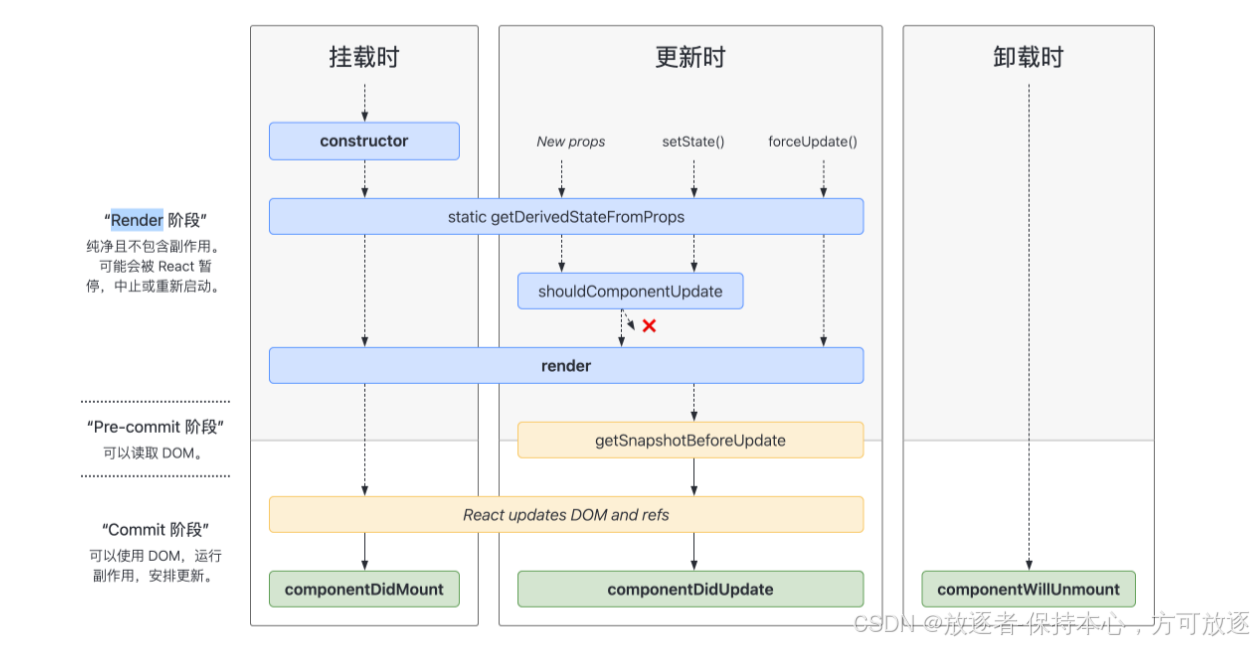
文章目录 一、React生命周期1. 挂载阶段(Mounting)补充2. 更新阶段(Updating)补充 static getDerivedStateFromProps 更新阶段应用补充 getSnapshotBeforeUpdate3. 卸载阶段(Unmounting) 二、React组件间的…...

关于 API
关于 API $set 问法:有没有遇到过数据更新了但视图没有更新的情况? <template><div>{{arr}}<button click"btn"></button></div> </template><script> export default {name:"Home"da…...

第15次CCF CSP真题解
1、小明上学 题目链接:https://sim.csp.thusaac.com/contest/15/problem/0 本题是模拟红绿灯计时的题,根据红绿灯转换规则可知,红灯后面通常是绿灯,绿灯后面是黄灯,黄灯过后又是红灯。根据题意,当k 0时&…...
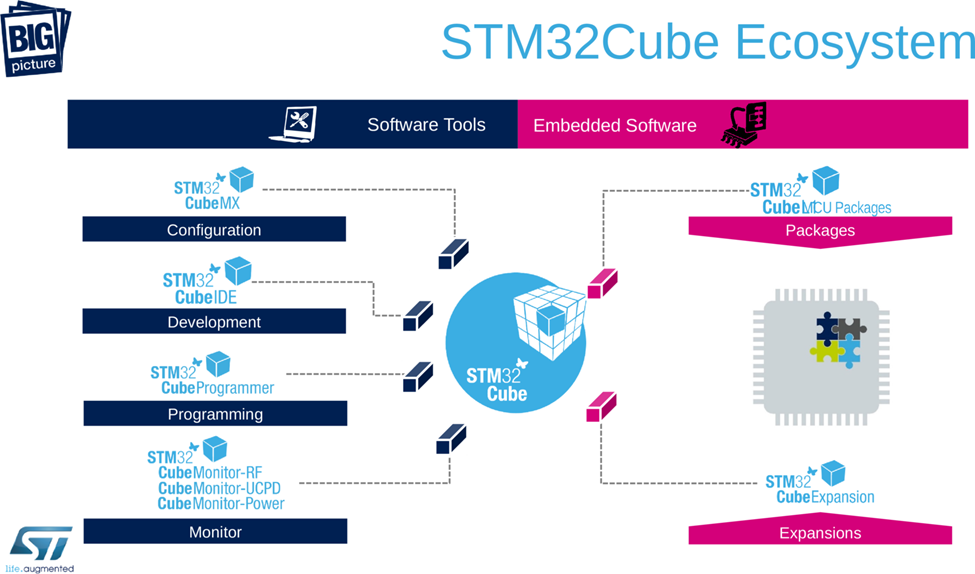
STM32硬件平台
STM32 系列是 STMicroelectronics 设计的高度灵活、广泛应用的微控制器(MCU)系列,支持从低功耗应用到高性能处理的需求,适用于工业、汽车、消费电子和物联网等广泛领域。STM32 系列具有广泛的硬件种类和丰富的功能,以下…...

一文讲明白大模型分布式逻辑(从GPU通信原语到Megatron、Deepspeed)
1. 背景介绍 如果你拿到了两台8卡A100的机器(做梦),你的导师让你学习部署并且训练不同尺寸的大模型,并且写一个说明文档。你意识到,你最需要学习的就是关于分布式训练的知识,因为你可是第一次接触这么多卡…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
