小小的表盘还能玩出这么多花样？华为手表这次细节真的拉满
没想到小小的表盘还能玩出这么多花样？华为这次细节真的拉满！还有没有你不知道的神奇玩法？
情绪·萌宠，心情状态抬腕可见
好心情就像生活馈赠的糖果，好的心情让我们遇到困难也不惧打击！HUAWEI WATCH GT 5情绪萌宠表盘，情绪状态随时可见，全天记录更贴心~超萌熊猫宝宝时刻陪伴你的每一种心情。HUAWEI WATCH GT 5‘表’露好心情，怎么开心怎么来~
免费表盘，"腕"转海量主题
小表盘，大地盘！我的表盘我做主~HUAWEI WATCH GT 5"腕"转免费海量主题，个性表盘随心换~上百款表盘任你选择，不管是轻奢商务，还是文艺复古，总能找到你的心选款哦！
趣味心情，每次抬腕都是状态表情包
趣味心情，你的腕间表情包~每次抬腕都有新可能！HUAWEI WATCH FIT 3专属黄豆表情包，每一个表情都代表一种个性态度，点一点还有互动效果，快看一看你的新状态是什么~
轻轻一碰，立即解锁专属表盘
手机手表，轻轻一碰，立即解锁新玩法~ HUAWEI WATCH FIT 3一碰传，手机照片轻轻一碰，秒变独特表盘!
相关文章：
小小的表盘还能玩出这么多花样？华为手表这次细节真的拉满
没想到小小的表盘还能玩出这么多花样？华为这次细节真的拉满！还有没有你不知道的神奇玩法？ 情绪萌宠，心情状态抬腕可见 好心情就像生活馈赠的糖果，好的心情让我们遇到困难也不惧打击！HUAWEI WATCH GT 5情绪…...
trueNas 24.10 docker配置文件daemon.json无法修改（重启被覆盖）解决方案
前言 最近听说truenas的24.10版本开放docker容器解决方案放弃了原来难用的k3s，感觉非常巴适，就研究了一下，首先遇到无法迁移老系统应用问题比较好解决，使用sudo登录ssh临时修改daemon.json重启docker后进行docker start 容器即可…...
数字孪生，概念、应用与未来展望
随着科技的飞速发展，数字化已经成为各行各业的发展趋势，在这个过程中，数字孪生作为一种新兴的技术，逐渐引起了人们的关注，本文将对数字孪生的概念、应用以及未来展望进行详细介绍。 数字孪生的概念： 数字孪…...
Chromium HTML Input 类型Text 对应c++
一、文本域（Text Fields） 文本域通过 <input type"text"> 标签来设定，当用户要在表单中键入字母、数字等内容时，就会用到文本域。 <!DOCTYPE html> <html> <head> <meta charset"ut…...
SpringMvc参数传递
首先对于post请求汉字乱码需要进行过滤器配置 普通参数传递 直接传递 客户端传递的属性名与我的bean中的函数参数名相同 映射传递RequestParam("XXX") 在我们方法参数中定义一个与客户端属性名一致 并绑定参数 POJO实体类传递 嵌套POJO传递 数组likes参数传递…...
西安国际数字影像产业园：数字化建设赋能产业升级与拓展
西安国际数字影像产业园的数字化建设，在当前经济与科技迅猛发展的大背景下，已然成为提升园区管理效率、服务水平以及运营效果的关键趋势。随着信息技术日新月异的进步，数字化更是成为这座产业园转型升级的核心关键词。如今，西安国…...
linux线程池
线程池: * 一种线程使用模式。线程过多会带来调度开销，进而影响缓存局部性和整体性能。而线程池维护着多个线程，等待着 监督管理者分配可并发执行的任务。这避免了在处理短时间任务时创建与销毁线程的代价。线程池不仅能够保证内核的充分利 用࿰…...
PyTorch图像分类实战——基于ResNet18的RAF-DB情感识别（附完整代码和结果图）
PyTorch图像分类实战——基于ResNet18的RAF-DB情感识别（附完整代码和结果图） 关于作者 作者：小白熊 作者简介：精通python、matlab、c#语言，擅长机器学习，深度学习，机器视觉，目标检测…...
【OccNeRF: Advancing 3D Occupancy Prediction in LiDAR-Free Environments】阅读笔记
【OccNeRF: Advancing 3D Occupancy Prediction in LiDAR-Free Environments】阅读笔记 1. 论文概述Abstract1. Introduction2. Related work2.1 3D Occupancy Prediction2.2 Neural Radiance Fields2.3 Self-supervised Depth Estimation 3. Method3.1 Parameterized Occupanc…...
DDRPHY数字IC后端设计实现系列专题之后端设计导入，IO Ring设计
本章详细分析和论述了 LPDDR3 物理层接口模块的布图和布局规划的设计和实 现过程，包括设计环境的建立，布图规划包括模块尺寸的确定，IO 单元、宏单元以及 特殊单元的摆放。由于布图规划中的电源规划环节较为重要， 影响芯片的布线资…...
EDA --软件开发之路
之前一直在一家做数据处理的公司，从事c开发，公司业务稳定，项目有忙有闲，时而看下c，数据库，linux相关书籍，后面跳槽到了家eda公司，开始了一段eda开发之路。 eda 是 electric design …...
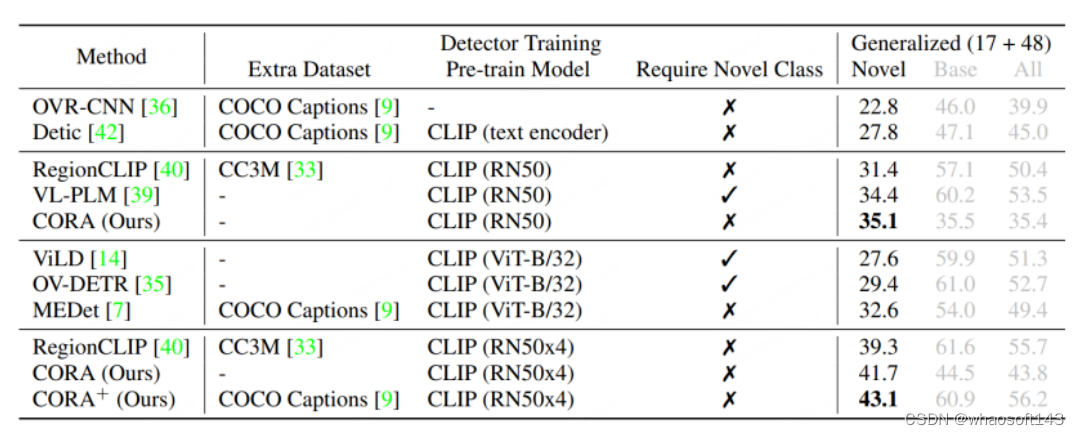
51c~目标检测~合集2
我自己的原文哦~ https://blog.51cto.com/whaosoft/12377509 一、总结 这里概述了基于深度学习的目标检测器的最新发展。同时，还提供了目标检测任务的基准数据集和评估指标的简要概述，以及在识别任务中使用的一些高性能基础架构，其还涵盖了…...
计算机低能儿从0刷leetcode | 33.搜索旋转排列数组
题目：33. 搜索旋转排序数组 思路：看到时间复杂度要求是O(log N)很容易想到二分查找，普通的二分查找我们已经掌握，本题中的数组可以看作由两个分别升序的数组拼成，在完全升序的部分中进行二分查找是容易的，…...
SpringBoot+VUE2完成WebSocket聊天(数据入库)
下载依赖 <!-- websocket --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId></dependency><!-- MybatisPlus --><dependency><groupId>com.ba…...
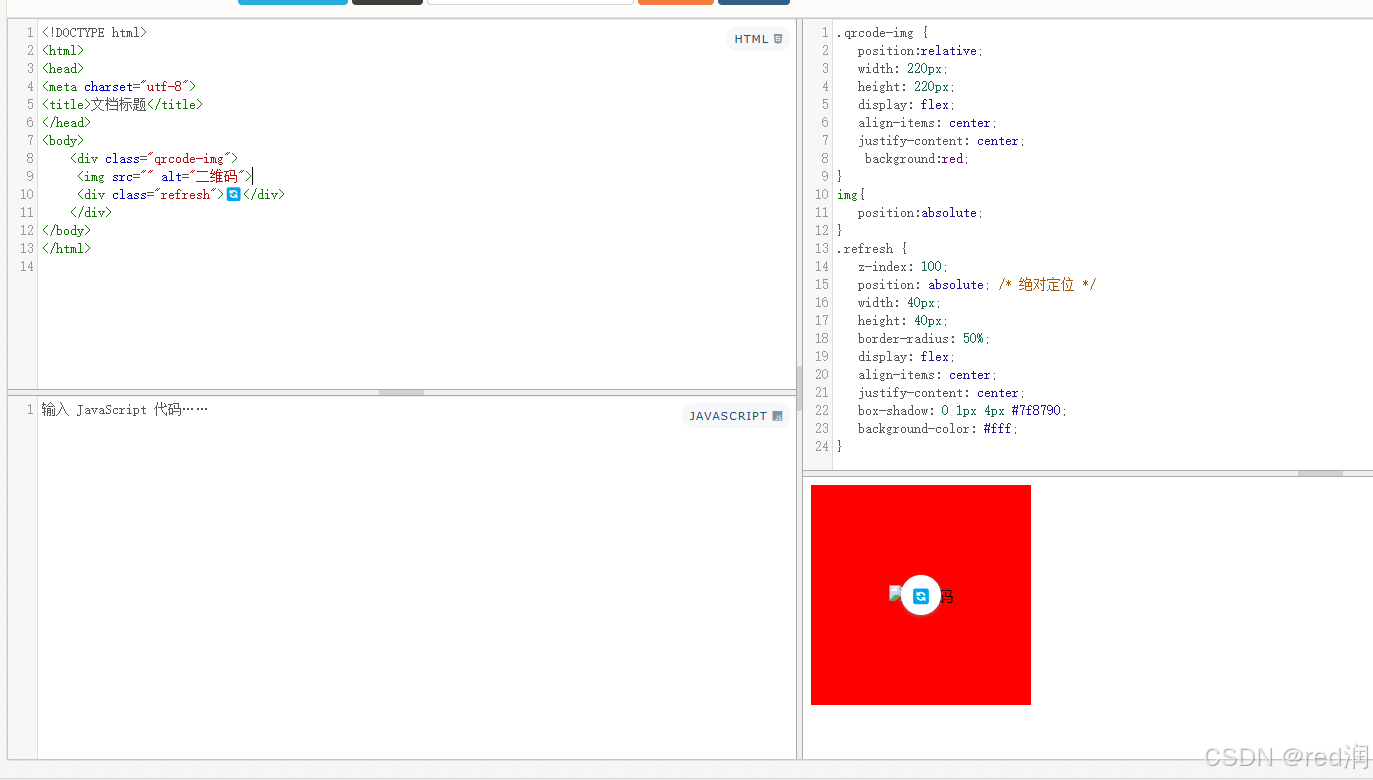
理解 CSS 中的绝对定位与 Flex 布局混用
理解 CSS 中的绝对定位与 Flex 布局混用 在现代网页设计中，CSS 布局技术如 flex 和绝对定位被广泛使用。然而，这两者结合使用时，可能会导致一些意想不到的布局问题。本文将探讨如何正确使用绝对定位元素，避免它们受到 flex 布局的…...
Redis 事务 问题
前言 相关系列 《Redis & 目录》《Redis & 事务 & 源码》《Redis & 事务 & 总结》《Redis & 事务 & 问题》 参考文献 《Redis事务详解》 Redis事务是什么？ 标准的事务是指执行时具备原子性/一致性/隔离性/持久性的一系列操作。…...
Cpp学习手册-进阶学习
C标准库和C20新特性 C标准库概览： 核心库组件介绍： 容器： C 标准库提供了多种容器，它们各有特点，适用于不同的应用场景。 std::vector： vector：动态数组，支持快速随机访问。 #in…...
代码随想录-字符串-反转字符串中的单词
题目 题解 法一:纯粹为了做出本题，暴力解 没有技巧全是感情 class Solution {public String reverseWords(String s) {//首先去除首尾空格s s.trim();String[] strs s.split("\\s");StringBuilder sb new StringBuilder();//定义一个公共的字符反转…...
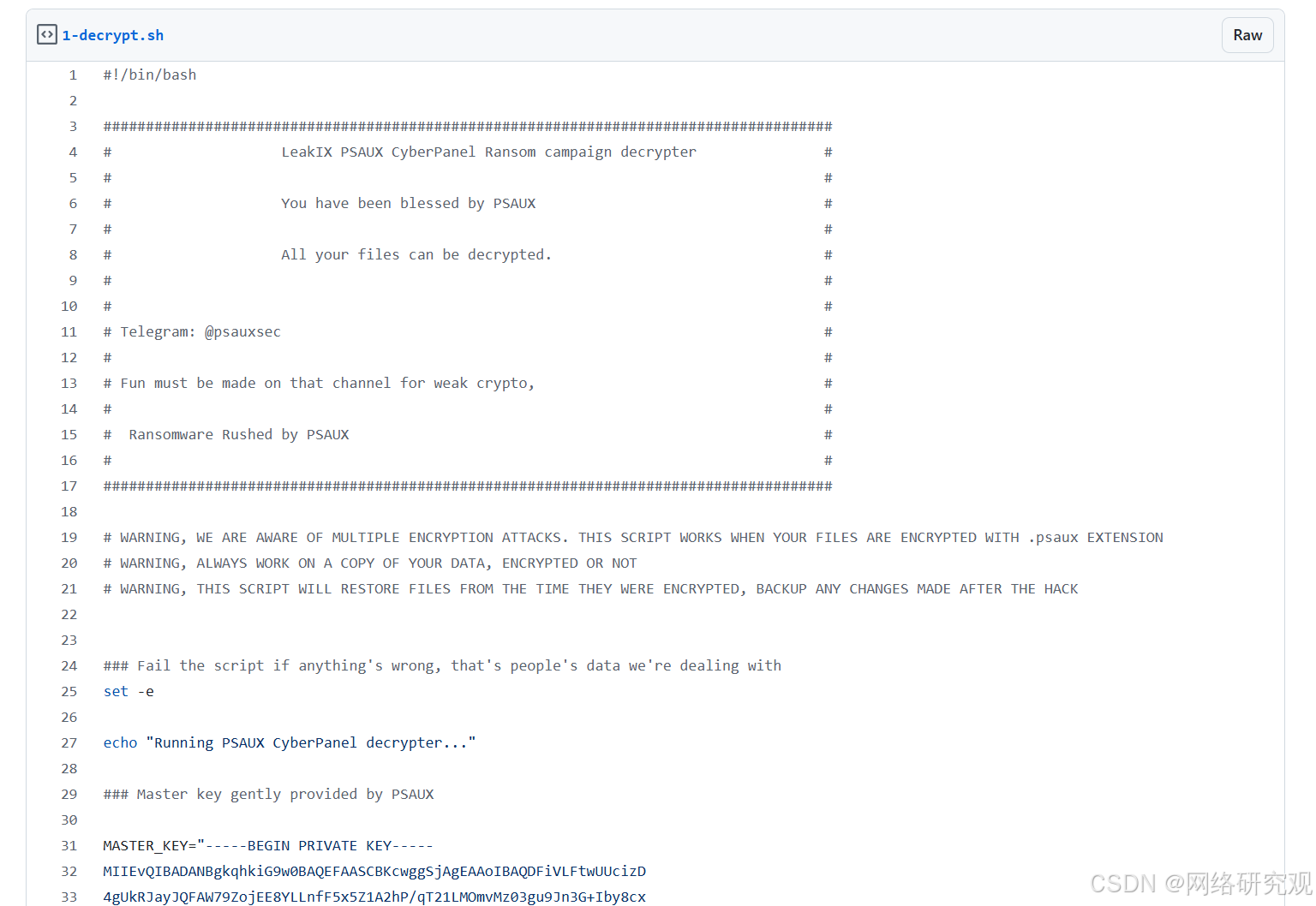
勒索软件通过易受攻击的 CyberPanel 实例攻击网络托管服务器
一个威胁行为者（或可能多个）使用 PSAUX 和其他勒索软件攻击了大约 22,000 个易受攻击的 CyberPanel 实例以及运行该实例的服务器上的加密文件。 PSAUX 赎金记录（来源：LeakIX） CyberPanel 漏洞 CyberPane…...
Open WebUI + openai API / vllm API ，实战部署教程
介绍Open WebUI + Ollama 的使用: https://www.dong-blog.fun/post/1796 介绍vllm 的使用：https://www.dong-blog.fun/post/1781 介绍 Ollama 的使用： https://www.dong-blog.fun/post/1797 本篇博客玩个花的，Open WebUI 本身可以兼容openai 的api， 那来尝试一下。 仅供…...
RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端，它允许HTTP与Elasticsearch 集群通信，而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展：显示创建时间8. 功能扩展：记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...
Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
【Zephyr 系列 10】实战项目：打造一个蓝牙传感器终端 + 网关系统（完整架构与全栈实现）
🧠关键词：Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者：希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数：约 5200 字 ✨ 项目总览 在物联网实际项目中，**“终端 + 网关”**是…...
css3笔记 （1） 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size：0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务： test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行！ sudo su - 1. CentOS 系统： yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件，或者在构建过程中仍然引用了旧的路…...
push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中，push 和 present 是两种不同的视图控制器切换方式，它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机，它可以执行Java字节码。Java虚拟机是Java平台的一部分，Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...