开关电源环路稳定性分析(11)——观察法找零极点
大家好,这里是大话硬件。
这篇文章主要是分享如何用观察法直接写出补偿网络中的零极点的表达式。
在前面的文章中,我们分别整理了OTA和OPA型的补偿网络,当时有下面的结论。
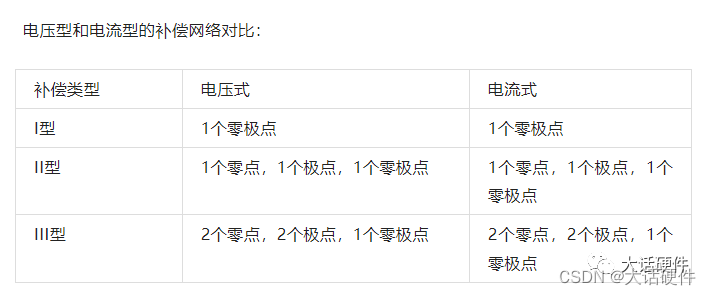
针对某个固定的补偿网络,我们可以用数学的方法推导补偿网络的零极点。比如下面OPA的I型补偿网络,求解零极点的过程如下:
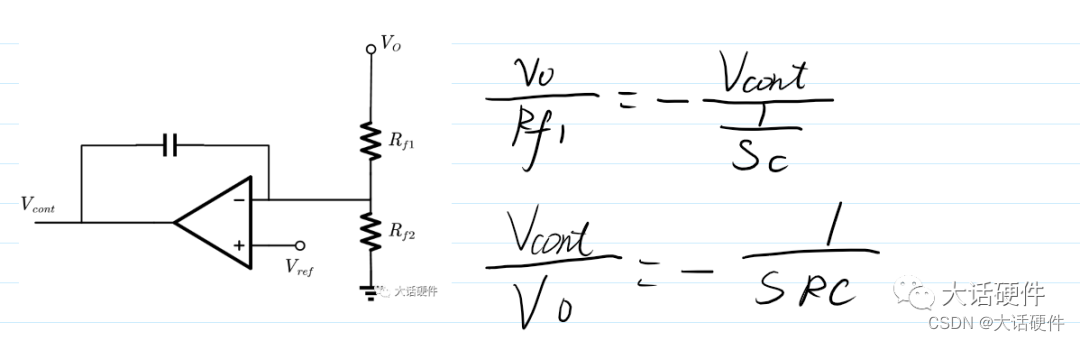
上面是纯粹数学方式求解的结果,从结果可以看出I型补偿只有极点,没有零点,相对来说还算简单。
下面求解II型补偿器的传递函数,写成标准零极点的形式:
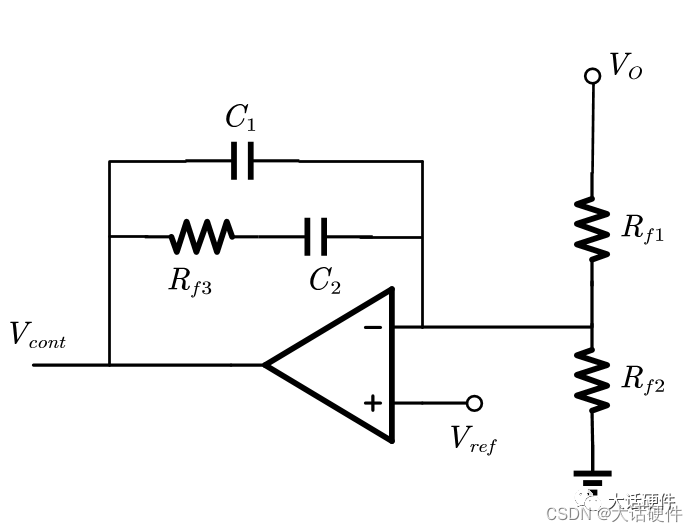

从上面的求解过程来看,是相当的复杂,而且这还是II型的补偿,换成III型的补偿,这个求解的过程会更复杂!
不信你看下面这个III型的补偿器,求解出的传递函数
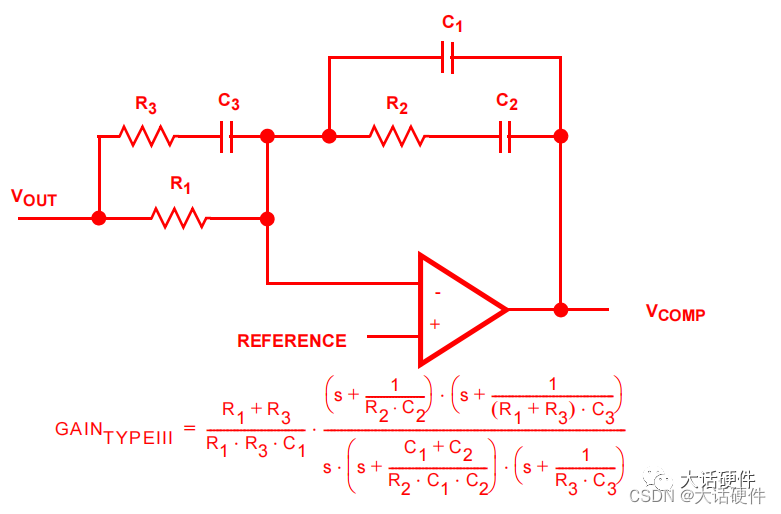
这是人家整理好的表达式,可以直接看出直流增益,零极点的位置。如果要是自己求解的,按照上面II型的方法,至少需要10分钟才能求解出来一个,而且还不一定对。
最近在开关电源大牛巴索的书里面找到一种简洁的方法求解零极点的方法,因此结合前面我自己都认为很复杂的过程,来看下这种简单的方法。
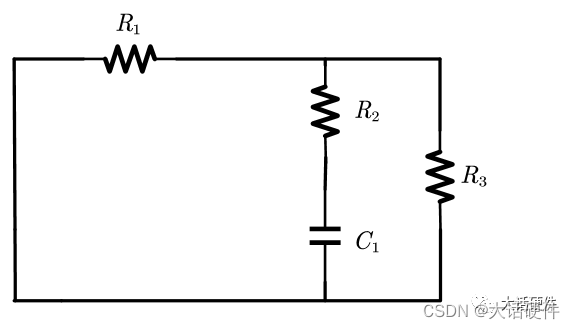
书中以一个简单的串并联电路为例:

对于这个网络,开始没人知道这个传递函数有几个零极点,也不知道是否存在零点和极点,但是由于只有电容一个存储元件,最后传递函数的表达式可以写成如下的结构:
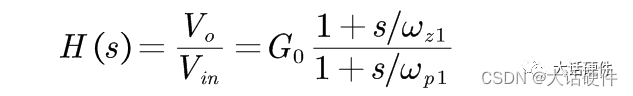
下面就是根据电路的性质,直接写成G,Wz,Wp的值,那么就可以得到传递函数的零极点。
首先是求解直流增益,即s=0,此时电容相当断开,所以G可以求出:
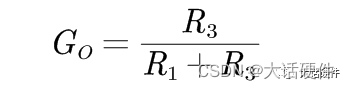
其次是求解零点,零点的定义是让激励信号永远不能到达输出的频率点,基于这个逻辑,我们需要找到电路中能阻止激励信号往输出传递的器件。
作者在书中提到了两种可能性:信号串联的时候,器件在这个频率点的阻抗的无穷大,或者这个器件在这个频率点将信号连接到地上形成短路。
基于以上两点作为前提,我们再看上述的网络:
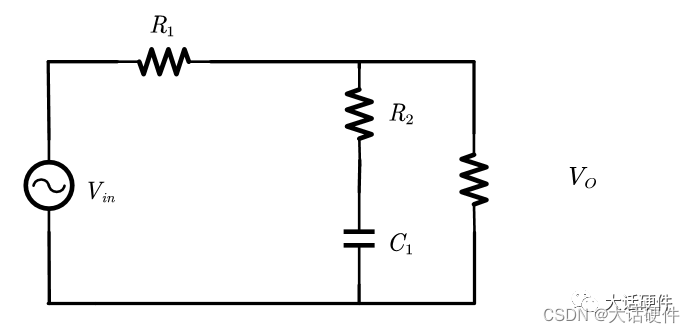
电容C是输出端的以并联的形式的加入,这是要满足两种可能性中的一种,只有一种情况,那就是R2+C1的阻抗为0,此时传递函数的分子为0。
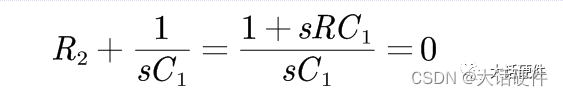
可以求出零点的位置
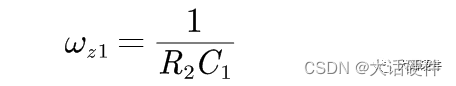
最后是求解传递函数的极点,求解极点的方法作者在书中介绍的是电路拓扑的时间常数,在求解的时候,电压源短路,电流源是开路,有点类似求解等效电阻的意思。
时间常数:
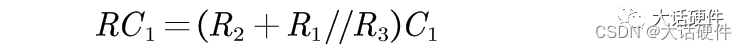
对于一阶系统,极点等效时间的常数,因此可以直接推导出极点:

所以系统的传递函数为:
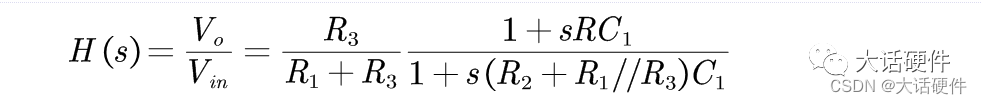
如果不用作者的方法,我自己也推导了一下,过程如下:

推导的过程明显比作者说的观察法难很多!!!
有了上面的内容,我们将上述的结论用在有补偿网络的传递函数里面。
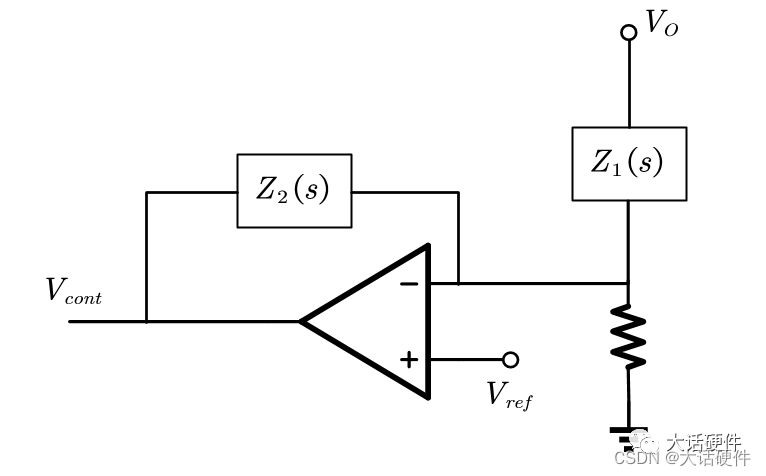
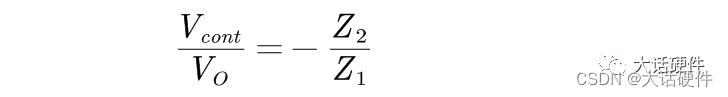
下面用前面的的理论来推导I型补偿网络的零极点:

零点,输出为0,分,子为0,则Z2=0,则1/Sc=0,则频率为无穷大,实际中确定RC参数,频率不可能无穷大,因此,I型补偿 网络没有零点。
极点,时间常数,Rf1C,所以存在极点:

推导II型补偿网络的零极点
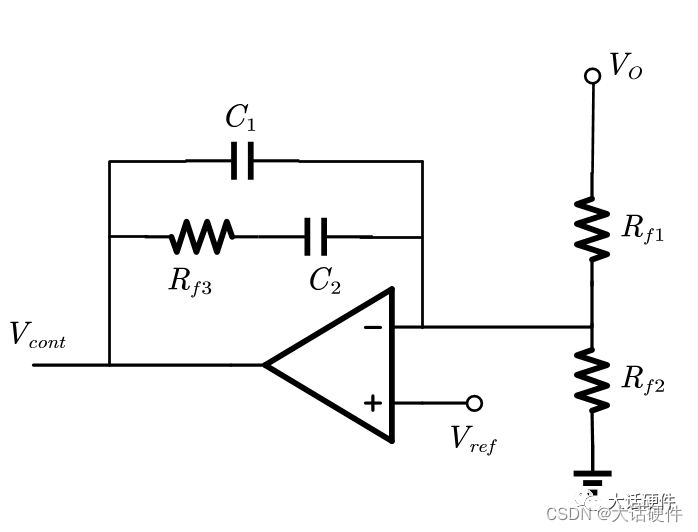
零点,输出为0,分子为0,则Z2=0,要使Z2的阻抗为0,C1的阻抗不能为0 ,只有RF3和C2的阻抗为0,因此,此时存在一个零点:

极点:极点是分母为0,在一阶系统中是求解电路网络结构的时间常数,而在在二阶系统中此种方法无法用。此时,可以借鉴零点的求法,极点的定义是让传递函数的分母为0,则整个系统的值为无穷大,那么Z2的阻抗为无穷大。
(1)当频率为0时,电容C1的阻抗为无穷大,此时存在零极点
(2)当频率为0时,电容RF3和C2的阻抗为无穷大,此时存在零极点
上述两个零极点的频率都是在频率为0,因此是同一个零极点
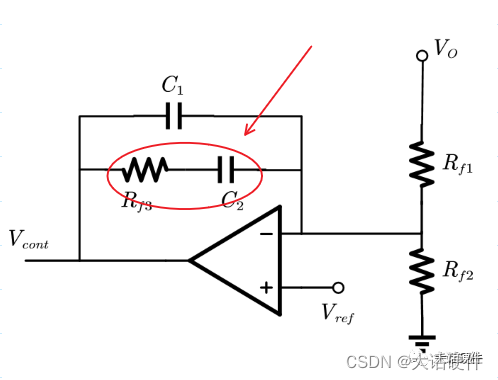
(3)当频率为f时,电容C1和RF3以及C2的串并联阻抗无穷大,除了频率为0的时刻,还存在另外一个频率f,即 Rf3+C2+C1的阻抗一起为无穷大
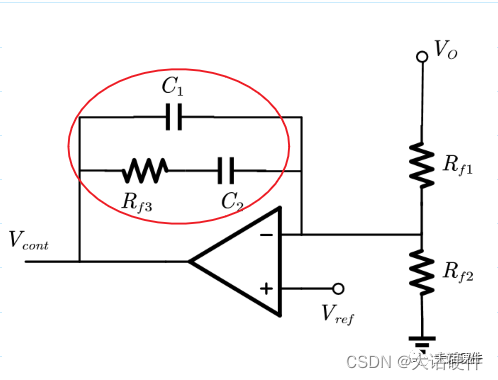
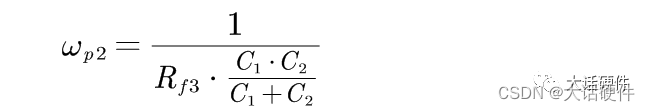
推导III型补偿网络的零极点
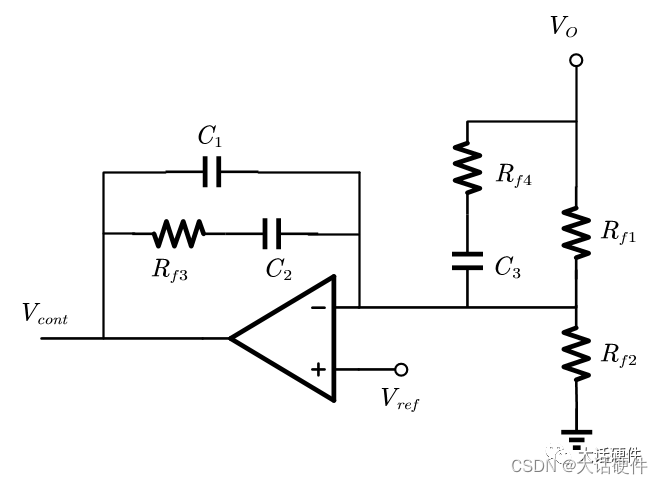
III型补偿相比II型补偿增加了一个电阻电容,推导方式和前面基本一致,但是增加的RF4,C3和电阻RF1之间可以有两种类型的组合。
当Rf4+C3阻抗为0时,系统增加一个极点,这样的频率是存在的,因此此时的极点为
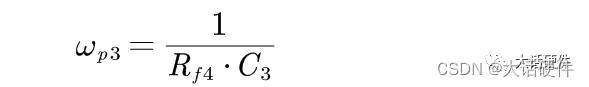
同理,Rf4+C3+RF1的阻抗为无穷大时,系统增加了一个零点,此时的零点
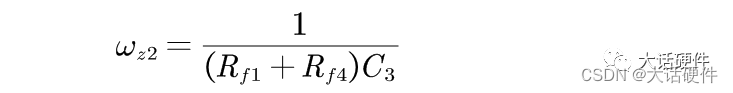
III型的另外几个零极点和II型的一样,这里不赘述。
上面的方面可以很快确定零极点,但是对于静态增益无法求出。对于复杂的系统,求解传递函数比较困难时,通过这种方法可以很快看出零极点。但是没办法将整个传递函数形式表达清楚,所以方法有利有弊。
文章中的方法来源于《开关电源控制环路设计》这本书,感兴趣的朋友在大话硬件公众号后台回复“环路设计”即可获取高清的电子中文版本。
相关文章:
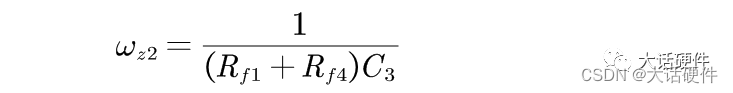
开关电源环路稳定性分析(11)——观察法找零极点
大家好,这里是大话硬件。 这篇文章主要是分享如何用观察法直接写出补偿网络中的零极点的表达式。 在前面的文章中,我们分别整理了OTA和OPA型的补偿网络,当时有下面的结论。 针对某个固定的补偿网络,我们可以用数学的方法推导补偿…...

焕新启航,「龙蜥大讲堂」2023 年度招募来了!13 场技术分享先睹为快
龙蜥大讲堂是龙蜥推出的系列技术直播活动,邀请龙蜥社区的开发者们分享围绕龙蜥技术展开,包括但不限于内核、编译器、机密计算、容器、储存等相关技术领域。欢迎社区开发者们积极参与,共享技术盛宴。往期回顾龙蜥社区技术系列直播截至目前已举…...
推广传单制作工具
临近节日如何制作推广活动呢?没有素材制作满减活动宣传单怎么办?小编教你如何使用在线设计工具乔拓云,轻松设计商品的专属满减活动宣传单,不仅设计简单,还能自动生成活动分享链接,只需跟着小编下面的设计步…...
数据结构(上))
软件设计(十一)数据结构(上)
线性结构 线性表 线性表是n个元素的有限序列,通常记为(a1,a2....an),特点如下。 存在唯一的一个称作“第一个”的元素。存在位移的一个称作“最后一个”的元素。除了表头外,表中的每一个元素均只有唯一的直接前趋除了表尾外&…...
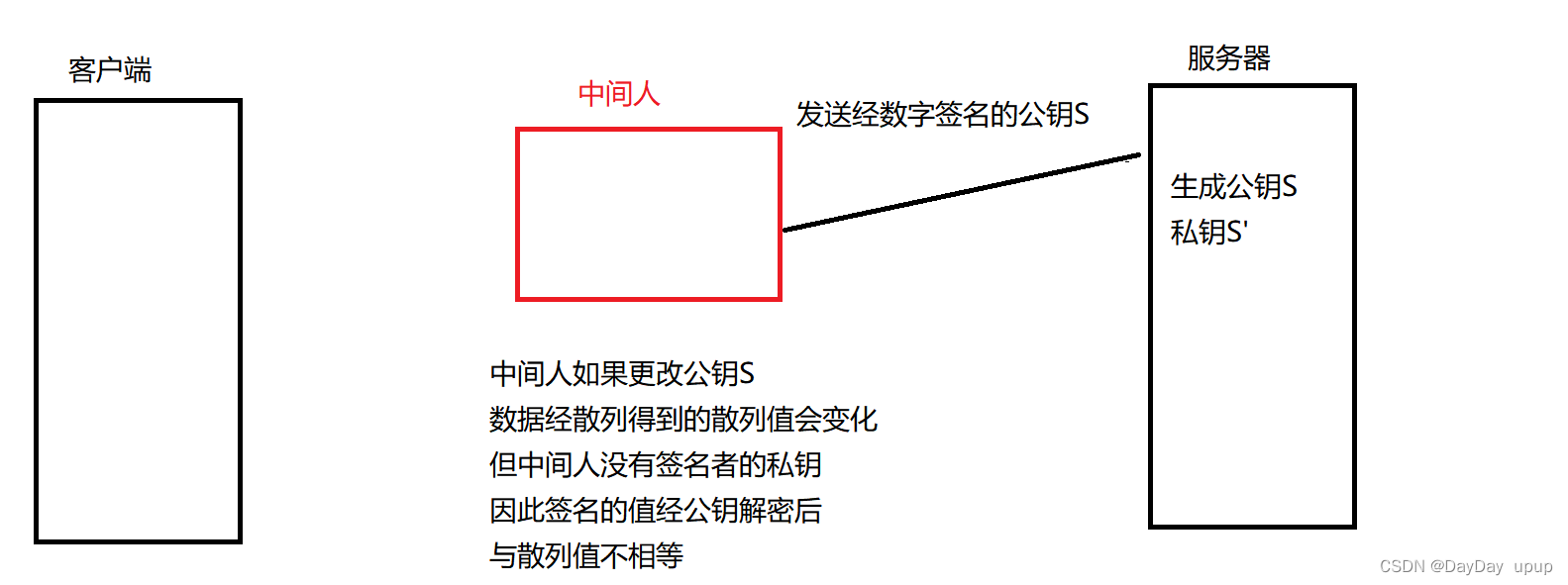
https协议
文章目录对称加密方案非对称加密方案对称加密方案非对称加密方案对称加密方案非对称加密方案数字证书因为HTTP是明文传输,所以会很有可能产生中间人攻击(获取并篡改传输在客户端及服务端的信息并不被人发觉),HTTPS加密应运而生。 …...
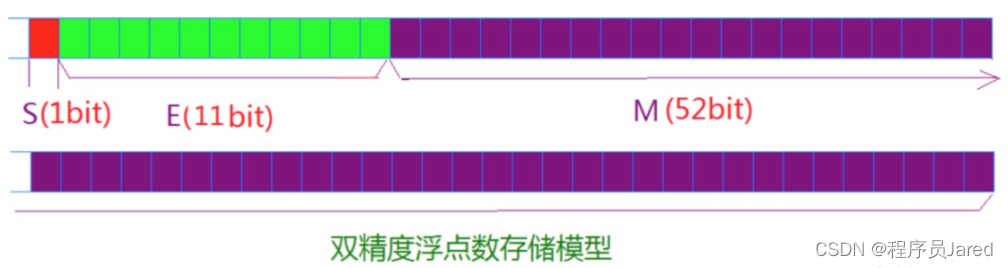
深入浅出C语言——数据在内存中的存储
文章目录一、数据类型详细介绍1. C语言中的内置类型2. 类型的基本归类:二. 整形在内存中的存储1. 原码、反码、补码2. 大小端三.浮点数存储规则一、数据类型详细介绍 1. C语言中的内置类型 C语言的内置类型有char、short、int、long、long long、float、double&…...

在 Centos 上在线安装 GitLab
作为程序员,其中一个愿望是拥有一个自己的代码存储库。在支持私有部署的代码存储库产品中,GitLab 是比较著名的了,所以今天我总结了一下在 Centos 上安装 GitLab 的过程。 依赖 基础依赖 首先,需要安装部分基础的依赖ÿ…...

模型解释性:SHAP包的使用
本篇博客介绍另一种事后可解释性方法:SHAP(SHapley Additive exPlanation)方法。 1. Shapley值理论 Shapley值是博弈论中的一个概念,通过衡量联盟中各成员对联盟总目标的贡献程度,从而根据贡献程度来进行联盟成员的利益分配,避免…...

算法训练营 day45 动态规划 0-1背包理论 分割等和子集
算法训练营 day45 动态规划 0-1背包理论 分割等和子集 0-1背包理论 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 在下面的讲解中&…...

SSM框架
1.mybatis的底层原理 本质上就是使用反射和动态代理来实现对应的映射关系 2.日志级别 3.传递参数 单个参数的传递和多个参数的传递 Emp selectOne(Param(“xingming”) String name); List selectByCondition(Param(“name”) String name,Param(“sal”) double sal); 4.#和…...

教育行业需要什么样的客服系统?
某教育公司拥有素质教育、成人教育、智慧教育等多个业务板块,日常通过电商、线上媒体、线上线下授课等方式进行业务开展和品牌宣传,取得了非常不错的成绩,受到了很多人的好评反馈。 对于这样一个教育公司,客户来源广泛࿰…...

花房集团任命新首席财务官:已跌破IPO发行价,活跃用户下滑
上市刚满2个月,花椒母公司花房集团(HK:03611)的高管就发生了变更。2023年2月12日,花房集团披露的公告显示,董事会宣布赵磊为该公司首席财务官(CFO),自2023年2月10日起生效。 据贝多…...

儿童绘本馆图书借阅租赁知识付费小程序源码交流
1.分类图书 2.书单推荐 4.会员卡次、期限购买 5.借阅时间选择 6.积分签到 7.优惠Q领取 前端uniapp开发 后端thinkphp开发 完全开源 <template> <view class"sp-section sp-index"> <!-- search --> <view class&qu…...

Vue3 中 axios 的安装及使用
目录前言:一、什么是 axios ?二、Axios 的配置项三、Axios 的请求方式四、自定义创建实例五、Axios 请求错误处理六、Axios 解决跨域问题七、Axios 请求案例随机笑话大全总结:前言: 在编写vue里的项目时,必须要用和后台…...

Django设计模式以及模板层介绍
MVC和MTV 传统的MVC作用:降低模块间的耦合度(解耦)Django的MTV模式 作用:降低模块间的耦合度(解耦)什么是模板 1、模板是可以根据字典数据动态变化的html网页2、模板可以根据视图中传递的字典数据动态生成相…...

Linux信号一门搞定
1.信号是什么? 信号其实就是一个软件中断。 例: 输入命令,在Shell下启动一个前台进程。用户按下Ctrl-C,键盘输入产生一个硬件中断。如果CPU当前正在执行这个进程的代码,则该进程的用户空间代码暂停执行,…...

手撸一个动态Feign,实现一个“万能”接口调用
Feign,在微服务框架中,是的服务直接的调用变得很简洁、简单,而不需要再编写Java Http调用其他微服务的接口。 动态feign 对于fegin调用,我们一般的用法:为每个微服务都创建对应的feignclient接口,然后为每…...
Linux Capabilities 入门
目录 Linux capabilities 是什么? capabilities 的赋予和继承 线程的 capabilities Permitted Effective Inheritable Bounding Ambient 文件的 capabilities Permitted Inheritable Effective 运行 execve() 后 capabilities 的变化 案例 Linux capab…...

驱动 day6
关于设备树的理解: 设备树(Device Tree)是一种用于特定硬件设备的解释语法树。它用来表示存储有关主板硬件和CPU架构信息的数据在内核中的传递格式,使内核可以更好地了解硬件并支持它们,而不必编写固定的代码。设备节点…...
附录2-tensorflow目标检测
源码来自作者Bubbliiiing,我对参考链接的代码略有修改,网盘地址 链接:百度网盘 请输入提取码 提取码:dvb1 目录 1 参考链接 2 环境 3 数据集准备 3.1 VOCdevkit/VOC2007 3.2 model_data/voc_classes.txt 3.3 voc_an…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
