子串分值【第十一届】【省赛】【A组】
问题描述
对于一个字符串 s,我们定义 s 的分值 f(s) 为 s 中恰好出现一次的字符个数。例如 f("aba")=1,f("abc")=3, f("aaa")=0。
现在给定一个字符串 s[0..n−1](长度为 n),请你计算对于所有 s 的非空子串 s[i..j](0≤i≤j<n),f(s[i..j])的和是多少。
输入格式
输入一行包含一个由小写字母组成的字符串 s。
输出格式
输出一个整数表示答案。
样例输入
ababc样例输出
21样例说明
子串 f值
a 1
ab 2
aba 1
abab 0
ababc 1b 1ba 2bab 1babc 2a 1ab 2abc 3b 1bc 2c 1评测用例规模与约定
对于 20% 的评测用例,1≤n≤10;
对于 40% 的评测用例,1≤n≤100;
对于 50% 的评测用例,1≤n≤1000;
对于 60% 的评测用例,1≤n≤10000;
对于所有评测用例,1≤n≤100000。
题解:
通俗地说,题目的要求就是给定一个字符串,要求求出这个字符串所有子串的分值,而对于一个字符串来说,它的分值就等于自身包含的所有字符中出现且仅出现了一次的字符个数。
顺着题意来的话,多数人应该会想要把给定字符串的子串全部枚举出来,然后再数每个子串中只出现了一次的字符的个数,这样做需要枚举所有的左右边界,计算的时间复杂度为O(n^2),必然会超时。
下面介绍的是O(n)的做法:
题目要求的分值是所有子串分值的总和,并且对于相同的字母a,如果它在不同的位置,它也算是不同的字母,比如给定字符串“aba”,他有子串‘a'和‘a’,两个‘a’在不同的位置。所以我们不需要计算所有子串的分值,只需要计算每一个字母作为只出现一次的字符时,包含了该字母的子串的个数,假如说现在给定一个字符串“abcadcada”,现在讨论字母a的分值,则可以把该字符串看成“a..bc..a..dc..a..d..a”,则对于第二个字母a,它的有效子串的个数9,分别为bca,ca,a,bcad,cad,ad,bcadc,cadc,adc;其实同样也是枚举左右边界,左边界有三种选择b、c、a,右边界有三种选择a、d、c,两两组合,组合数为3*3=9。对于其它字母也是同样的计算有效子串的个数,最终求解它们的和。
用一个数组pre[]预处理位于i左侧的和第i个字母相同的最近的一个字母的位置,“a..bc..a..dc..a..d..a”,对于第二个a来说,它是第四个字符,所以pre[4]=1;用一个数组next[]预处理位于i右侧的和第i个字母相同的最近的一个字母的位置,对于第二个a来说,next[4]=7.
所以左边界的选择数其实就等于“a..bc..a..dc..a..d..a”中bca的长度,右边界的选择数就等于“a..bc..a..dc..a..d..a”中adc的长度,转化为代码就是i - pre[i]和next[i] - i,将两者相乘,得到第二个子串的有效子串数。
在预处理pre和next数组时,会借助一个idx数组,由于题中给出的字符串都由小写字母组成,我们可以把每个字母都通过ascii码相减转化为数字也就是,x-'a',例如,‘b’-‘a’=1。所以idx[1]就表示上一个b出现的位置。
结合代码:
#include <iostream>
#include <string>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10, M = 50;
int pre[N], nex[N], idx[M];int main()
{string s; cin >> s;int len = s.size();s = ' ' + s;//计算pre[i]for (int i = 1; i <= len; i++) {pre[i] = idx[s[i] - 'a'];idx[s[i] - 'a'] = i;}//初始化右超界为n+1for (int i = 0; i < 26; i++) {idx[i] = len + 1;}//计算next[i]for (int i = len; i > 0; i--) {nex[i] = idx[s[i] - 'a'];idx[s[i] - 'a'] = i;}ll ans = 0;for (int i = 1; i <= len; i++) {ans += (i - pre[i]) * (nex[i] - i);}cout << ans;return 0;
}相关文章:

子串分值【第十一届】【省赛】【A组】
问题描述 对于一个字符串 s,我们定义 s 的分值 f(s) 为 s 中恰好出现一次的字符个数。例如 f("aba")1,f("abc")3, f("aaa")0。 现在给定一个字符串 s[0..n−1](长度为 n),请你计算对于…...
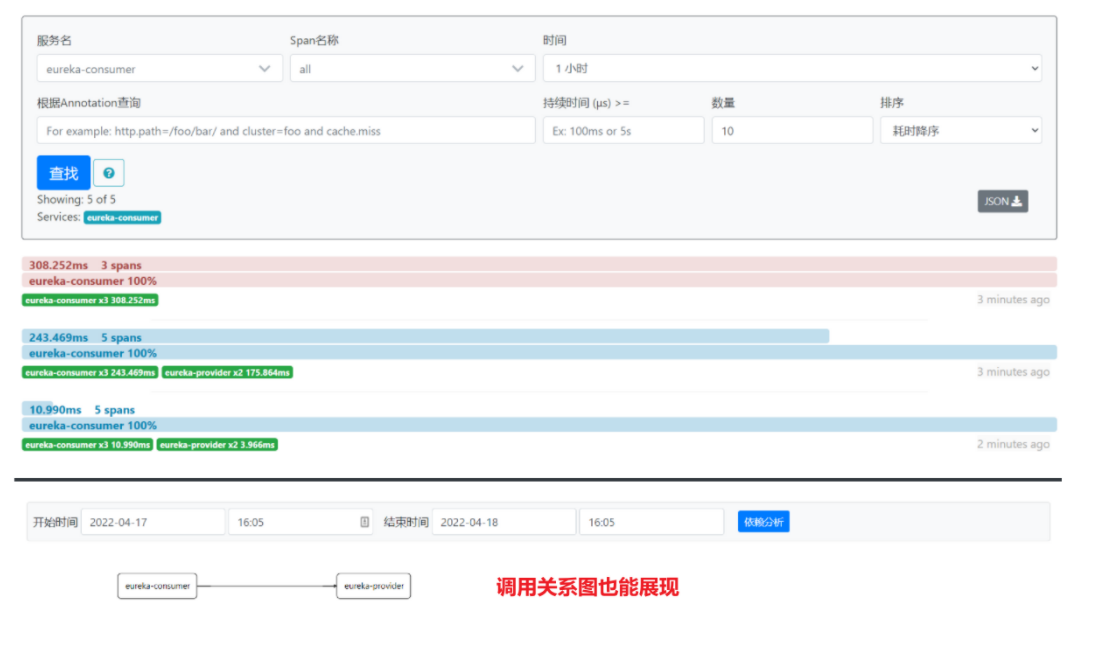
SpringCloud 中 Config、Bus、Stream、Sleuth
文章目录🚏 第十三章 分布式配置中心🚬 一、Config 概述🚬 二、Config 快速入门🚭 config-server:🛹 1、使用gitee创建远程仓库,上传配置文件🛹 2、导入 config-server 依赖…...

Quantum 构建工具使用新的 TTP 投递 Agent Tesla
Zscaler 的研究人员发现暗网上正在出售名为 Quantum Builder 的构建工具,该工具可以投递 .NET 远控木马 Agent Tesla。与过去的攻击行动相比,本次攻击转向使用 LNK 文件。 Quantum Builder 能够创建恶意文件,如 LNK、HTA 与 PowerShell&…...

浏览器中的 JavaScript 执行机制
思维导图 本文为反复学习极客时间-《浏览器的工作原理与实践》-浏览器中的 JavaScript 执行机制章节中的一些思考与记录。 一些重要概念 变量提升 所谓的变量提升,是指在 JavaScript 代码执行过程中,JavaScript 引擎把变量的声明部分和函数的声明部分…...

kafka集群搭建及问题
一、zookeeper集群搭建 1、创建文件夹 cd /home mkdir zookeeper 2、下载 cd zookeeper wget https://downloads.apache.org/zookeeper/zookeeper-3.8.0/apache-zookeeper-3.8.0-bin.tar.gz 解压到当前文件夹 tar -zxvf apache-zookeeper-3.8.0-bin.tar.gz 文件夹重命…...
不要忽视web渗透测试在项目中起到的重要性
在当前数字化环境中,IT的一个里程碑式增长便是公司组织和企业数字化。为了扩大市场范围和方便业务,许多组织都在转向互联网。这导致了一股新的商业浪潮,它创造了网络空间中的商业环境。通过这种方式,公司和客户的官方或机密文件都…...
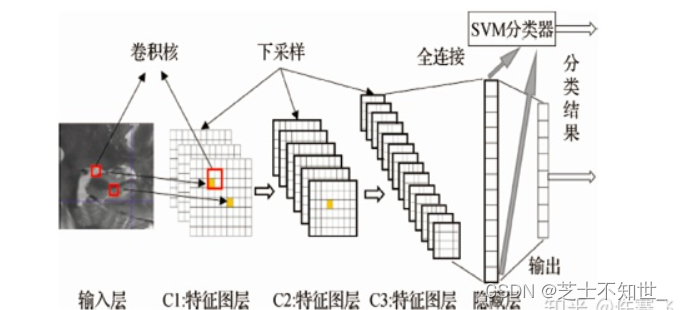
Early Stopping中基于测试集(而非验证集)上的表现选取模型的讨论
论文中一般都是用在验证集上效果最好的模型去预测测试集,多次预测的结果取平均计算准确率或者mAP值,而不是单纯的取一次验证集最好的结果作为论文的结果。如果你在写论文的过程中,把测试集当做验证集去验证的话,这其实是作假的&am…...

appium ios真机自动化环境搭建运行(送源码)
appium ios真机自动化环境搭建&运行(送源码) 目录:导读 (1)安装JDK,并配置环境变量,方法如下: (2)安装Xcode、Xcode commandline tools和iOS模拟器 &…...
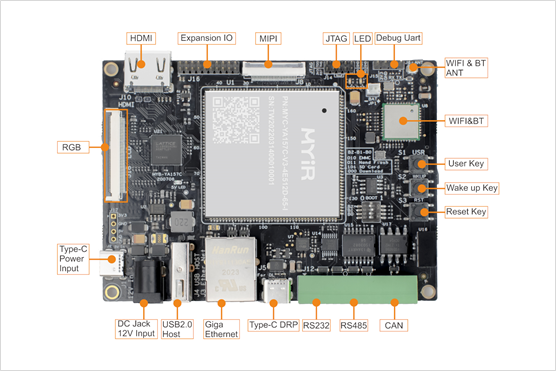
米尔基于ARM嵌入式核心板的电池管理系统(BMS)
BMS全称是Battery Management System,电池管理系统。它是配合监控储能电池状态的设备,主要就是为了智能化管理及维护各个电池单元,防止电池出现过充电和过放电,延长电池的使用寿命,监控电池的状态。 图片摘自网络 电池…...
Java后端项目IDEA配置代码规范检查,使用checkStyle实现
最近的Java后端项目想实现代码的规范检查,调研了一圈,终于找到了简单的方式实现:以下是常见的几种方案: 1、在客户端做 git hook,主要是用 pre-commit 这个钩子。前端项目中常见的 husky 就是基于此实现的。但缺点也很…...
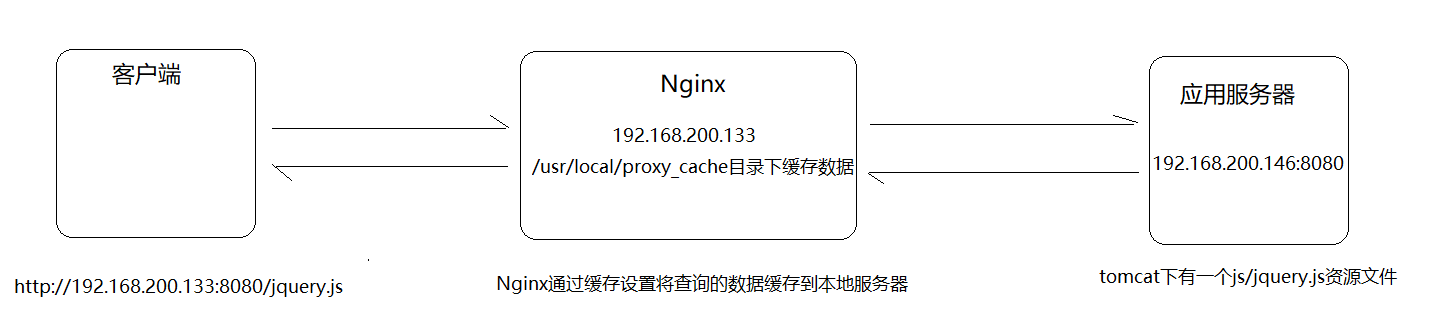
Nginx_4
Nginx负载均衡 负载均衡概述 早期的网站流量和业务功能都比较简单,单台服务器足以满足基本的需求,但是随着互联网的发展,业务流量越来越大并且业务逻辑也跟着越来越复杂,单台服务器的性能及单点故障问题就凸显出来了,…...
linux Ubuntu KUbuntu 系统安装相关
系统安装 本来想快到中午的时候调试一下服务器上的http请求接收代码。我的电脑上装的是kali的U盘系统,然后我的U盘居然找不到了(然后之前安装的系统不知道是否是写入软件的原因,没办法解析DNS,我都用的转发的,这让我体验非常差。kali的系统工具很多&…...

个人信息保护认证
个人信息保护认证是证明个人信息处理者在认证范围内开展的个人信息收集、存储、使用、加工、传输、提供、公开、删除以及跨境等处理活动符合认证依据标准要求。适用范围 本规则依据《中华人民共和国认证认可条例》制定,规定了对个人信息处理者开展个人信息收集、存储…...

Negative Prompt in Stable Diffusion
必读链接:https://www.reddit.com/r/StableDiffusion/comments/z7salo/with_the_right_prompt_stable_diffusion_20_can_do/ A lot of people have noticed that Negative Prompt works wonders in 2.0, and works even better in 2.1. Negative hints are the op…...

MLX90316KGO-BDG-100-RE传感器 旋转位置 角度测量
介绍MLX90316是Tria⊗is旋转位置传感器,提供在设备表面旋转的小偶极磁铁(轴端磁铁)的绝对角位置。得益于其表面的集成磁集中器(IMC),单片设备以非接触式方式感知应用磁通量密度的水平分量。这种独特的传感原理应用于旋转位置传感器,可在机械(…...
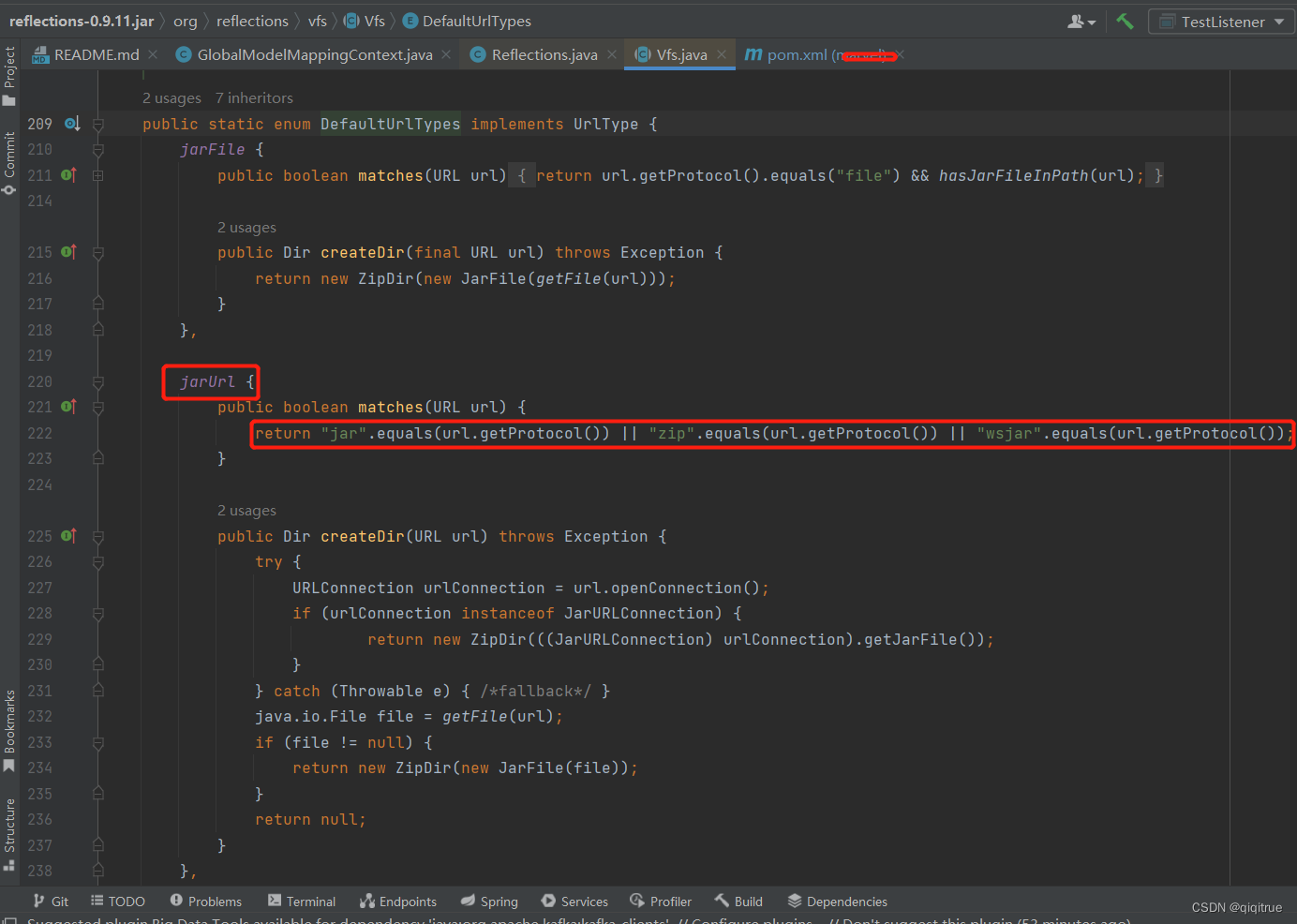
Reflections反射包在springboot jar环境下扫描不到class排查过程
需求: 要实现指定pkg(如com.qiqitrue.test.pojo)扫描包下所有class类信息:使用代码如下 使用的版本:0.10.2(截至目前是最新版)发现只能在idea编译期间可以获取得到(也就是在开发阶段…...
黑马】后台项目171集
将近一个月没有练习了,找到之后果然打不开出了问题【问题】运行代码打开网页后,发现不能正常登录,一开始还以为是密码记错了,后来发现是数据库没有正常启动,phpstudy中的数据库一直是启动状态,关闭不了。【…...
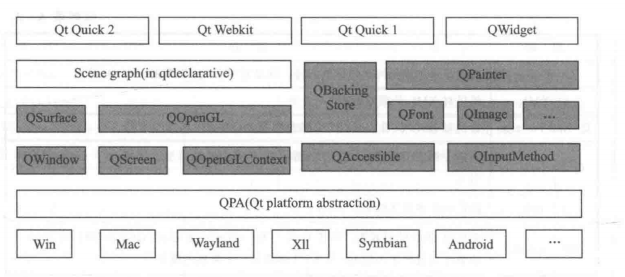
Qt 5 架构和特点
Qt 5 模块构架: 模块:功能:Qt CoreQt 5 的核心类库,每个模块都建立在Core上Qt GUI图形用户界面开发的最基础的类库Qt Widgets提供c用户界面部件(是对Qt GUI的拓展)Qt SQL对数据库进行操作Qt Multimedia、…...
)
转换符说明使用方法(在printf函数中)
目录 一些常见的转换说明及打印结果: printf()的转换说明修饰符 printf()函数打印数据指令时要与代打印数据的类型相匹配才行。 如%d %c %ld......这些符号叫做转换说明。代表着数据转化成显示的形式。 一些常见的…...

针灸-基本任脉督脉
这里写自定义目录标题 丈量 同身丈下针深浅一般入穴的方法成人 幼儿 不同入穴方式现代常用针概念十二经 纳天干**天干**地支表里关系筋络任脉中脘穴:梅花灸巨阙穴廉泉穴督脉长强腰俞命门阳关悬枢脊中筋缩眼诊 癫痫至阳消渴...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
