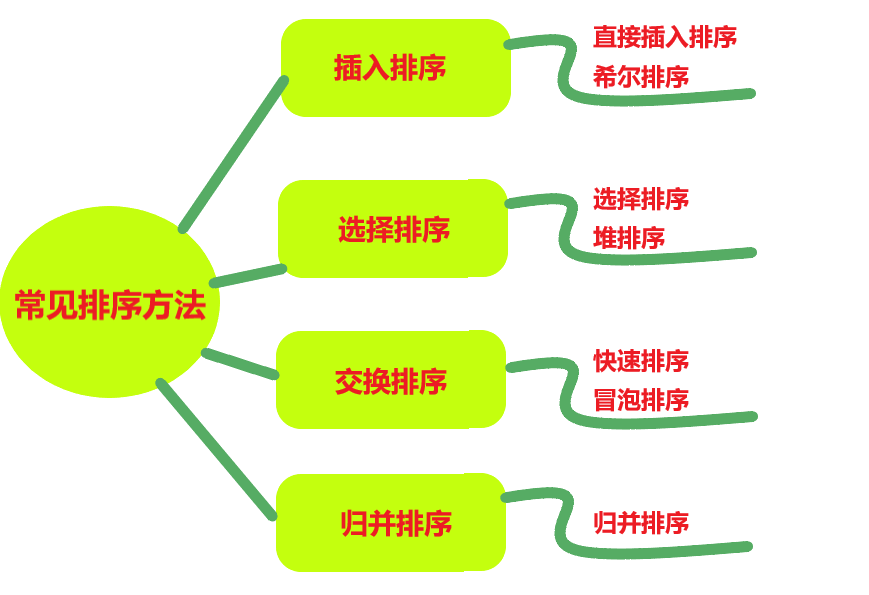
【数据结构-JAVA】排序
排序在现实生活中的应用可谓相当广泛,比如电商平台中,选购商品时,使用价格排序或是综合排序、高考填报志愿的时候,会参考全国大学排名的情况。
下面介绍一些计算机中与排序相关的概念:
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持 不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳 定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
插入排序
1.1 直接插入排序
1.1.1 插入排序的基本思想
把待排序的记录按其关键码值的大小与已经排好序的序列逐个比较大小,插入到合适的位置,使整个序列重新有序。实际中我们玩扑克牌时,就用了插入排序的思想。
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…array[0]的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移。
1.1.2 直接插入法的代码实现
public class Test {public static void insertSort(int[] arr){for (int i = 1; i < arr.length; i++) {int j = i - 1;int temp =arr[i];for (; j >= 0 ; j--) {if(arr[j] > temp){arr[j+1] = arr[j];}else{break;}}arr[j + 1] = temp;}}public static void main(String[] args) {int[] arr = {4,2,5,3,134,74,36,7,8,76,32,17,38,54,38,87,54};insertSort(arr);System.out.println(Arrays.toString(arr));}
}输出:
[2, 3, 4, 5, 7, 8, 17, 32, 36, 38, 38, 54, 54, 74, 76, 87, 134]
1.1.3 直接插入法的特性总结
直接插入排序的特性总结: 1. 元素集合越接近有序,直接插入排序算法的时间效率越高 2. 时间复杂度:O(N^2) 3. 空间复杂度:O(1) 4. 稳定性:稳定 ,它是一种稳定的排序算法
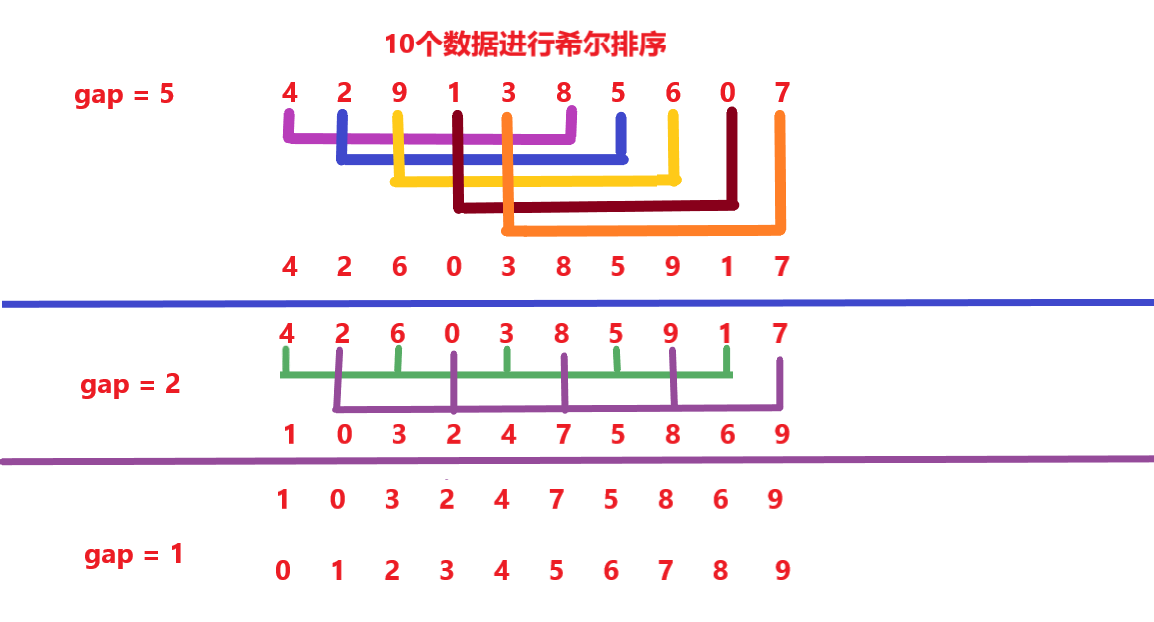
1.2 希尔排序
1.2.1 希尔排序的基本思想
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先想好间隔的设定方法,比如gap一开始为数组的长度,那么每个记录自成一组,无需排序,往后的间隔依次除以2(可以自己设定),把待排序文件中所有记录分成gap个组, 并对每一组内的记录进行直接插入排序。然后重复上述分组和排序的工作。当gap =1时,所有记录在统一组内最后插入排序。
1.2.2 希尔排序的代码实现
//希尔排序:对直接插入法的优化public static void shellSort(int[] arr){int gap = arr.length;while(gap >= 1){gap /= 2;shell(arr,gap);}}private static void shell(int[] arr, int gap) {for (int i = gap; i < arr.length; i++) {int j = i - gap;int temp = arr[i];for (; j >= 0 ; j-=gap) {if(arr[j] > temp){arr[j + gap] = arr[j];}else{break;}}arr[j + gap] = temp;}}public static void main(String[] args) {int[] arr = {5,23,2,51,4,5,642,14,56,82,1,73,59,42,77};shellSort(arr);System.out.println(Arrays.toString(arr));}输出:
[1, 2, 4, 5, 5, 14, 23, 42, 51, 56, 59, 73, 77, 82, 642]
1.2.3 希尔排序的特性总结
希尔排序的特性总结: 1. 希尔排序是对直接插入排序的优化。 2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很 快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。 3. 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算。Knuth进行了大量的试验统计 ,当n很大时,关键码平均比较次数以及对象平均移动次数大约在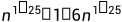 范围内。所以对于希尔排序的时间复杂度,我们暂时就按照
范围内。所以对于希尔排序的时间复杂度,我们暂时就按照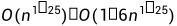 来计算。 4. 稳定性:不稳定
来计算。 4. 稳定性:不稳定
2. 选择排序
2.1 直接选择排序
2.1.1 直接先择排序的基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置。此时,就有1个元素有序,那么继续从剩下待排序元素中找到最小(或最大)的一个元素,放到有序数组后面,直到全部待排序的数据元 素排完 。
写代码时,如果是在原本数组进行操作,那么只能让序列的最小值与相应位置进行交换了。
2.1.2 直接选择排序的代码实现
//选择排序//从一边查找最小元素public static void selectSort(int[] arr){//i下标是排序的位置//j则是遍历剩下数组元素,找到最小下标for (int i = 0; i < arr.length; i++) {int j = i + 1;int minIndex = i;for (; j < arr.length; j++) {if(arr[j] < arr[minIndex]){minIndex = j;}}swap(arr,i,minIndex);}}public static void main(String[] args) {int[] arr = {3,7,54,24,33,22,18,33,28,13,64,8,26};selectSort(arr);System.out.println(Arrays.toString(arr));}输出:
[3, 7, 8, 13, 18, 22, 24, 26, 28, 33, 33, 54, 64]
为了让选择排序更高效,能不能在序列中查找最小值的同时,查找最大值,让最小值与最大值与各自相应位置进行交换?
//从序列同时查找最大最小元素并与相应位置上的元素进行交换public static void selectSort(int[] arr){int left = 0;int right = arr.length - 1;while(left < right){int minIndex = left;int maxIndex = left;for (int j = left + 1; j <= right; j++) {if(arr[j] < arr[minIndex]){minIndex = j;}if(arr[j] > arr[maxIndex]){maxIndex = j;}}swap(arr,minIndex,left);if(left == maxIndex){maxIndex = minIndex;}swap(arr,maxIndex,right);left++;right--;}}public static void main(String[] args) {int[] arr = {4,3,22,56,77,23,53,7,13,75,224,6,27,69,49,88};selectSort(arr);System.out.println(Arrays.toString(arr));}输出:
[3, 4, 6, 7, 13, 22, 23, 27, 49, 53, 56, 69, 75, 77, 88, 224]
2.1.3 直接排序的特定
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用 2. 时间复杂度:O(N^2) 3. 空间复杂度:O(1) 4. 稳定性:不稳定
2.2 堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆 来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
2.2.1 堆排序的代码实现
//堆排序,从小到大 -> 建立大堆 ; 从大到小 -> 建立小堆public static void heapSort(int[] arr){if(arr == null){return;}createHugeHeap(arr);int end = arr.length - 1 ;while(end > 0){swap(arr,0,end);shiftDown(arr,0,end);end--;}}//向下调整:private static void shiftDown(int[] arr,int parent,int len){int child = 2 * parent + 1;while(child < len){if(child + 1 < len && arr[child] < arr[child + 1]){child++;}if(arr[child] > arr[parent]){swap(arr,child,parent);parent = child;child = 2 * parent + 1;}else{break;}}}private static void createHugeHeap(int[] arr){for (int parent = (arr.length - 1 - 1)/2; parent >= 0 ; parent--) {shiftDown(arr,parent,arr.length );}}public static void main(String[] args) {int[] arr = {76,35,62,5,62,43,55,13,27,28,33,2,79,1};Sort.heapSort(arr);System.out.println(Arrays.toString(arr));}输出:
[1, 2, 5, 13, 27, 28, 33, 35, 43, 55, 62, 62, 76, 79]
2.2.2堆排序的特性
【堆排序的特性总结】 1. 堆排序使用堆来选数,效率就高了很多。 2. 时间复杂度:O(N*logN) 3. 空间复杂度:O(1) 4. 稳定性:不稳定
3. 交换排序
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特 点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
3.1 快速排序
3.1.1 快速排序的基本思想
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元 素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有 元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
3.1.2 快速排序的代码实习
public static void quickSort(int[] arr){quick(arr,0,arr.length - 1);}private static void quick(int[] arr, int start, int end) {if(start >= end){return;}//int pivot = partition(arr,start,end);int pivot = partition1(arr,start,end);quick(arr,start,pivot - 1);quick(arr,pivot + 1,end);}填坑法
//填坑法private static int partition(int[] arr,int left,int right){int temp = arr[left];while(left < right){//这里的等号不能省略,否则会陷入死循环//而有了等号,left < right 这个条件就不能省略while(left < right && arr[right] >= temp){right--;}swap(arr,right,left);while(left < right && arr[left] <= temp){left++;}swap(arr,left,right);}arr[left] = temp;return left;}Hoare法
//Hoare 法private static int partition1(int[] arr,int left,int right){int temp = arr[left];int i = left;while(left < right){while(left < right && arr[right] >= temp){right--;}while(left < right && arr[left] <= temp){left++;}swap(arr,left,right);}swap(arr,left,i);return left;}上述的快速排序有一个问题,那就是如果数组已经是有序或是逆序的情况下,再次快排,每次都没有左树或是右数,比较费空间和时间,时间复杂度会达到O(N²),而且空间复杂度达到O(N),而只有每次划分都很平均的情况下,时间复杂度会达到O(NlogN),而且空间复杂度达到O(logN)。所以这里可以采用三数取中法来对快速排序进行优化。
三数取中法优化快排
//三数取中法:优化快排private static int midThree(int[] arr,int head ,int tail ,int mid){if(arr[head] > arr[tail]){if(arr[mid] > arr[head]){return head;}else if(arr[tail] > arr[mid]){return tail;}else{return mid;}}else{if(arr[mid] > arr[tail]){return tail;}else if(arr[mid] < arr[head]){return head;}else{return mid;}}}//上述quick 方法修改如下:private static void quick(int[] arr, int start, int end) {if(start >= end){return;}int mid = (start + end)/2;int midIndex = midThree(arr,start,end,mid);swap(arr,mid,start);//int pivot = partition(arr,start,end);int pivot = partition1(arr,start,end);quick(arr,start,pivot - 1);quick(arr,pivot + 1,end);}public static void main(String[] args) {int[] arr = {9,8,7,6,5,4,3,2,1,0};Sort.quickSort(arr);System.out.println(Arrays.toString(arr));}快排的非递归实现
public static void quickSortNor(int[] arr){int left = 0;int right = arr.length - 1;int pivot = partition(arr,left,right);Deque<Integer> stack = new LinkedList<>();if(pivot - 1 > left){stack.push(pivot - 1);stack.push(left);}if(right > pivot + 1){stack.push(right);stack.push(pivot + 1);}while(!stack.isEmpty()){left = stack.pop();right = stack.pop();pivot = partition(arr,left,right);if(pivot - 1 > left){stack.push(pivot - 1);stack.push(left);}if(right > pivot + 1){stack.push(right);stack.push(pivot + 1);}}
}3.1.3 快速排序的特点
1. 快速排序整体的综合性能和使用场景都是比较好的,所以才叫快速排序 2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(logN) 4. 稳定性:不稳定
3.2 冒泡排序
3.2.1 冒泡排序的代码实现
//改进之后的冒泡排序:public static void bubbleSort(int[] arr){for (int i = 0; i < arr.length - 1; i++) {boolean flag = false;for (int j = 0; j < arr.length - 1 - i; j++) {if(arr[j] > arr[j + 1]){swap(arr,j,j+1);flag = true;}}if(flag == false){return;}}}public static void main(String[] args) {int[] arr = {2,35,7,245,65,24,26,12,15,2,52,74,55,29,39,6};Sort.bubbleSort(arr);System.out.println(Arrays.toString(arr));}输出:
[2, 2, 6, 7, 12, 15, 24, 26, 29, 35, 39, 52, 55, 65, 74, 245]
3.2.2 冒泡排序的特点
【冒泡排序的特性总结】 1. 冒泡排序是一种非常容易理解的排序 2. 时间复杂度:O(N^2) 3. 空间复杂度:O(1) 4. 稳定性:稳定
4. 归并排序
4.1 归并排序的基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使 子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
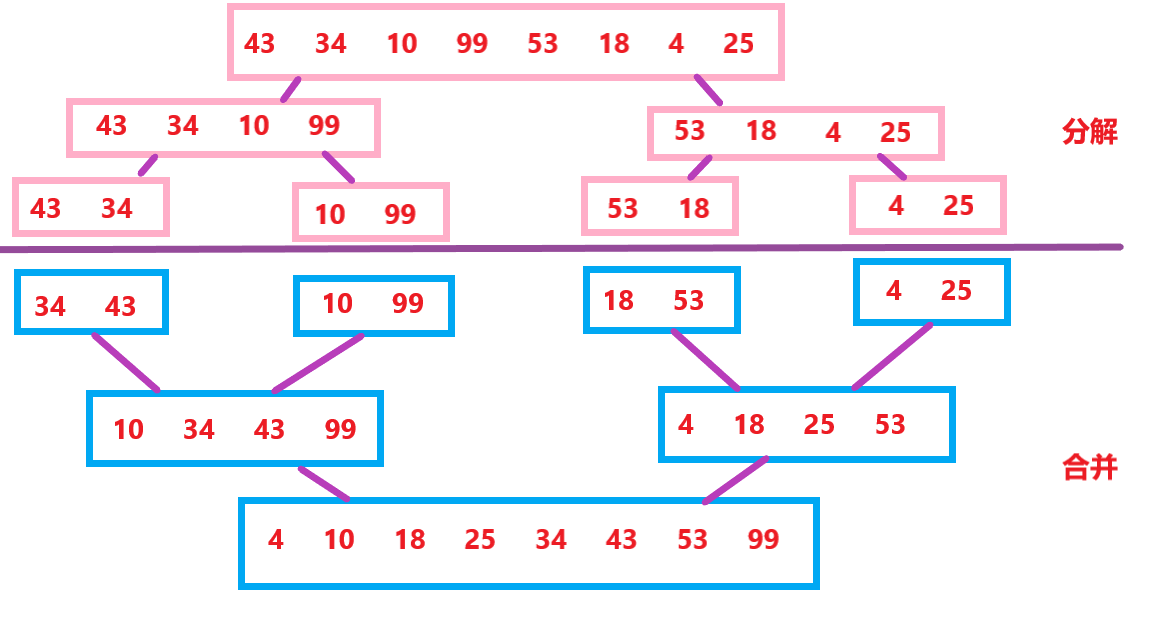
4.2 归并排序的代码实现
递归实现归并排序
public static void mergeSort(int[] arr){divide(arr,0,arr.length - 1);
}private static void divide(int[] arr,int left,int right){if(left >= right){return;}int mid = (left + right)/2;divide(arr,left,mid);divide(arr,mid+1,right);merge(arr,left,right,mid);
}private static void merge(int[] arr, int start, int end, int mid) {int s1 = start;int s2 = mid + 1;int[] temp = new int[end - start + 1];int k = 0;while(s1 <= mid && s2 <= end){if(arr[s1] < arr[s2]){temp[k++] = arr[s1++];}else{temp[k++] = arr[s2++];}}while(s1 <= mid){temp[k++] = arr[s1++];}while(s2 <= end){temp[k++] = arr[s2++];}for (int i = 0; i < temp.length; i++) {arr[start + i] = temp[i];}}非递归实现归并排序
public static void mergeSort(int[] arr){int gap = 1;while(gap < arr.length){for (int i = 0; i < arr.length; i += 2 * gap) {int left = i;int mid = left + gap - 1;if(mid >= arr.length){mid = arr.length - 1;}int right = mid + gap;if(right >= arr.length){right = arr.length - 1;}merge(arr,left,right,mid);}gap *= 2;}}4.3 归并排序的特点
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。 2. 时间复杂度:O(N*logN) 3. 空间复杂度:O(N) 4. 稳定性:稳定
5. 其他排序
5.1 计数排序
5.1.1 计数排序的基本思想
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤: 1. 统计相同元素出现次数 2. 根据统计的结果将序列回收到原来的序列中
5.1.2 计数排序的代码实现
public static void countSort(int[] arr){int max = arr[0];int min = arr[0];for (int i = 1; i < arr.length; i++) {if(arr[i] > max){max = arr[i];}if(arr[i] < min){min = arr[i];}}int[] count = new int[max - min + 1];for (int i = 0; i < arr.length; i++) {count[arr[i] - min]++;}int k = 0;for (int i = 0; i < count.length; i++) {while(count[i] > 0){arr[k] = i + min;k++;count[i]--;}}}5.1.3 计数排序的特点
【计数排序的特性总结】
1. 计数排序在数据范围集中时,效率很高,是一种不需要比较大小的排序方式,但是适用范围及场景有限。
2. 时间复杂度:O(MAX(N,范围))
3. 空间复杂度:O(范围)
4. 稳定性:稳定
相关文章:

【数据结构-JAVA】排序
排序在现实生活中的应用可谓相当广泛,比如电商平台中,选购商品时,使用价格排序或是综合排序、高考填报志愿的时候,会参考全国大学排名的情况。下面介绍一些计算机中与排序相关的概念:排序:所谓排序…...

基于注解管理Bean
一、介绍从 Java 5 开始,Java 增加了对注解(Annotation)的支持,它是代码中的一种特殊标记,可以在编译、类加载和运行时被读取,执行相应的处理。开发人员可以通过注解在不改变原有代码和逻辑的情况下&#x…...

Containerd 的 Bug 导致容器被重建!如何避免?
作者简介邓宇星,SUSE Rancher 中国区软件架构师,6 年云原生领域经验,参与Rancher 1.x 到 Rancher 2.x 版本迭代,目前负责 Rancher For openEuler(RFO) 项目开发。最近我们关注到一个关于 containerd 运行时的 issue(https://g…...
win环境安装部署Jenkins
win环境安装部署Jenkins,2022年11月:从2022年 6 月 28 日发布的 Jenkins 2.357 和2022年9 月发布的 LTS 版本开始,Jenkins 需要 Java 11 才能使用,放弃 Java 8,如果用JDK1.8,那么Jenkins版本需要是2.357版本…...

网络变压器与不同芯片之间的匹配原则及POE通讯产品需要注意哪些方面
Hqst盈盛电子导读:网络变压器与不同芯片之间的匹配原则及POE通讯产品需要注意哪些方面网络变压器与不同芯片之间的匹配原则:一,电流型PHY芯片一般要配的网络变压器:1、变压器PHY侧3线共模电感 (更适合POE产品ÿ…...

Spring WebFlux
目录 基于注解编程模型 函数式编程模型 传统的基于Servlet的Web框架,如Spring MVC,在本质上都是阻塞和多线程的,每个连接都会使用一个线程。在请求处理的时候,会在线程池中拉取一个工作者( worker )线程来对请求进行处理。同时,请求线程是阻塞的,直到工作者线程提示它已…...

C++基础面试题:new和malloc的区别
面试题:new和malloc的区别或new和malloc的异同 相同点: 1、new/delete和malloc/free它们都是内存申请和释放的函数。 2、new/delete和malloc/free 都要一一对应,调用了多少次new 就需要调用多少次delete;同 理调用多少次ma…...

WebDAV之葫芦儿·派盘+KMPlayer
KMPlayer 支持WebDAV方式连接葫芦儿派盘。 KMPlayer几乎可以播放您系统上所有的影音文件,支持几乎全部音视频格式。通过其强大的插件功能,可以支持层出不穷的新格式。软件还具有齐全的操控功能,支持捕获音频、捕获AVI、捕获画面、外挂字幕、自定义编辑设置,是视频爱好者的不…...
企业登记工作(2023年度)的通知)
杨浦区人工智能及大数据(云计算)企业登记工作(2023年度)的通知
各相关单位: 根据《“长阳秀带”在线新经济产业集聚发展若干政策》(杨府发〔2022〕2号)及其实施细则的要求,现组织开展2023年度杨浦区人工智能与大数据(云计算)企业登记备案工作,现将相关工作通知如下: 一…...

2023年去培训机构学前端还是Java?
选择专业肯定是优先考虑更有发展前景和钱途的专业。毕竟IT专业的培训费都不低,基本都要一两万左右,咱们花钱总是希望获得最大回报。 那么到底哪个更有发展前景呢? 零基础能学得会吗? 就业薪资如何呢? 前言 不知道大家有…...

【React】组件事件
React(二) 创建组件 函数组件 函数组件:使用JS的函数或者箭头函数创建的组件 使用 JS 的函数(或箭头函数)创建的组件,叫做函数组件约定1:函数名称必须以大写字母开头,React 据此区分组件和普通的 HTML约定2:函数组…...

黑/白盒测试说明
白盒测试白盒测试也称结构测试或逻辑驱动测试,它是按照程序内部的结构测试程序,通过测试来检测产品内部动作是否按照设计规格说明书的规定正常进行,检验程序中的每条通路是否都能按预定要求正确工作。白盒测试的测试方法有代码检查法、静态结…...

车道线检测-Eigenlanes 论文学习笔记
论文:《Eigenlanes: Data-Driven Lane Descriptors for Structurally Diverse Lanes》 代码:https://github.com/dongkwonjin/Eigenlanes 核心:在 Eigenlane Space 中检测车道线 创新点 Eigenlane:数据驱动的车道描述符ÿ…...

docker run mysql -e 的环境变量 Environment Variables
例子 sudo docker run -itd --name DockerMysqlLatest3307 -p 3307:3306 -e MYSQL_ROOT_PASSWORDroot的密码 mysql:latest### root无密码 sudo docker run -itd --name Mysql57 -p 57:3306 -e MYSQL_ALLOW_EMPTY_PASSWORDroot mysql:5.7https://hub.docker.com/_/mysql?tabde…...

第17章 MongoDB 条件操作符教程
第17章 MongoDB 条件操作符教程 描述 条件操作符用于比较两个表达式并从mongoDB集合中获取数据。 在本章节中,咱们将讨论如何在MongoDB中使用条件操作符。 MongoDB中条件操作符有: (>) 大于 - $gt(<) 小于 - $lt(>) 大于等于 - $gte(< …...
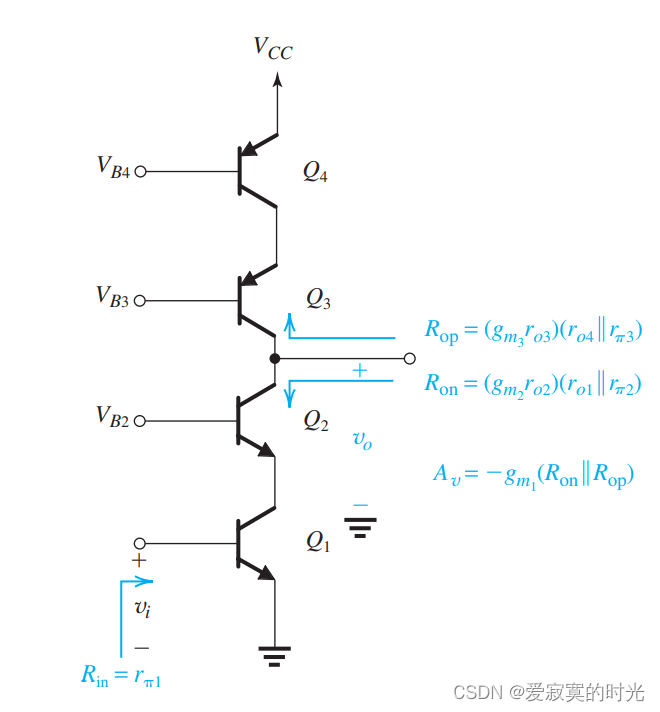
电子技术——共源共栅放大器
电子技术——共源共栅放大器 之前我们提到过,提高基础增益单元(共源放大器)的一种方法是提高其 ror_oro 的阻值,之后我们学过共栅放大器作为电流缓冲器可以做到这一点,自然地我们就得到了终极解决方案,也…...
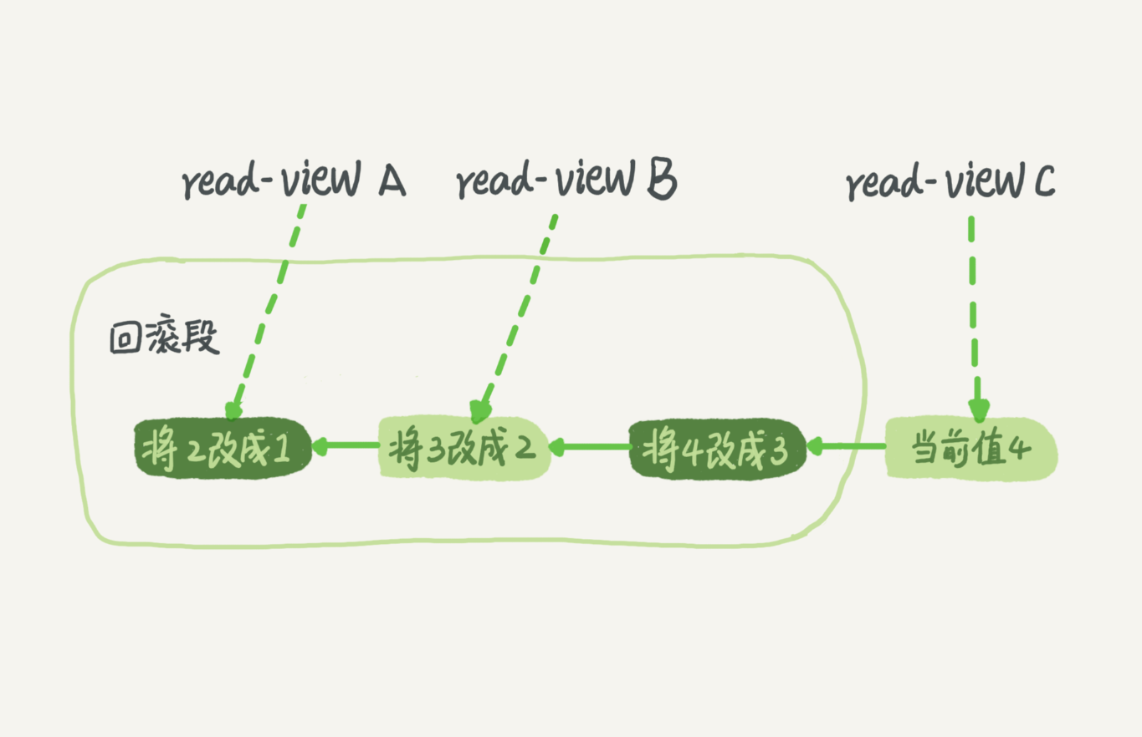
《MySQL学习》 事务隔离 与 MVCC
《MySQL学习》 事务隔离 一.事务的概念 事务保证一组数据要么全部成功要么全部失败,MySQL的事务基于引擎(如InnoDB)实现。 二.事务的隔离性与隔离级别 MySQL的标准隔离级别: 读未提交 : 一个事务还没提交时&#…...
html(二)基础标签
一 HTML中的注释 重点: 在哪写注释? 注释的形式? vs code和webstorm都可以通过 ctrl / 进行单行注释和取消注释 ① html中注释的形式 1) html文档中单行和多行注释是"<!-- -->" -->html2) 在html文档中,script标签…...
leetcode刷题---递归思想
leetcode刷题---递归思想)1.1 递归介绍1.2 基本步骤1.3 代表题目1.3.1 入门题---青蛙跳1.3.2.1 初级题226.翻转二叉树112.路径总和1.3.3 中级题---汉诺塔问题1.3.4 进阶题---细胞分裂1.1 递归介绍 如果在函数中存在着调用函数本身的情况,这种现象就叫递…...
ThreadLocal 源码级别详解
ThreadLocal简介 稍微翻译一下: ThreadLocal提供线程局部变量。这些变量与正常的变量不同,因为每一个线程在访问ThreadLocal实例的时候(通过其get或set方法)都有自己的、独立初始化的变量副本。ThreadLocal实例通常是类中的私有静…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
