Python奇异值分解
当AAA是方阵时,可以很容易地进行特征分解:A=WΣW−1A=W\Sigma W^{-1}A=WΣW−1,其中Σ\SigmaΣ是AAA的特征值组成的对角矩阵。如果WWW由标准正交基组成,则W−1=WTW^{-1}=W^TW−1=WT,特征分解可进一步写成WTΣWW^T\Sigma WWTΣW。
然而,当AAA不是方阵时,情况大不一样了,但仍然可以将AAA表示成A=UΣVTA=U\Sigma V^TA=UΣVT的形式,其中Σ\SigmaΣ也是对角矩阵,对角线上的每个元素被称作奇异值。
奇异值的求解过程和特征值息息相关,因为把AAA变成方阵很简单,只要乘以转置就行。故令L=AATL=AA^TL=AAT,R=ATAR=A^TAR=ATA,则L,RL, RL,R都可以求特征值λi\lambda_iλi和特征向量,其中LLL的特征向量为AAA的左奇异向量,RRR的特征向量为右奇异向量。对应的奇异值σi=λi\sigma_i=\sqrt{\lambda_i}σi=λi。
numpy.linalg中提供了奇异值分解函数svd,参数为
svd(a, full_matrices=True, compute_uv=True, hermitian=False)
其中
a待分解矩阵,维度为(M, N)full_matrices若为True,则U, Vh分别为(M, M)和(N, N);否则分别为(M, K), (K, N),K为M, N中较小的那个compute_uv如果为False则不计算U, Vhhermitian为True时,表示处理的是实对称矩阵
scipy.linalg中也提供了奇异值分解函数svd,其参数为
svd(a, full_matrices=True, compute_uv=True, overwrite_a=False, check_finite=True, lapack_driver='gesdd')
其中与numpy.linalg相同的参数,其意义也相同,不相同的部分,各参数含义如下
overwrite_a如果为True,则直接对a进行修改check_finite如果为True,则进行有限性检查lapack_driverSVD分解的方法,有两个选择'gesdd'效率更高'gesvd'此为Matlab和R中使用的方法
其返回值即U,Σ,VTU, \Sigma, V^TU,Σ,VT。
scipy.linalg还提供了两个和SVD相关的函数,svdvals(a)用于求a的奇异值;diagsvd(s, M, N)通过s, M, N,创建一个Σ\SigmaΣ矩阵。
下面测试一下svd
import numpy as np
import scipy.linalg as sl
a = np.random.rand(5,5)
u1, s1, vh1 = sl.svd(a)
u2, s2, vh2 = np.linalg.svd(a)
print(s1)
# [2.63698545 0.94063722 0.36159198 0.21052102 0.19014115]
print(s1-s2)
# [ 0.0 0.0 1.11022302e-16 -2.77555756e-17 0.0]
numpy和scipy的结果是几乎相同的,下面测试一下不同方法进行奇异值分解的时间
from timeit import timeit
a = np.random.rand(1000,1000)
timeit(lambda:sl.svd(a), number=10)
# 1.870287900000001
timeit(lambda:np.linalg.svd(a), number=10)
# 13.355788999999998
timeit(lambda:sl.svd(a, lapack_driver='gesvd'), number=10)
# 3.873418600000001
相关文章:

Python奇异值分解
当AAA是方阵时,可以很容易地进行特征分解:AWΣW−1AW\Sigma W^{-1}AWΣW−1,其中Σ\SigmaΣ是AAA的特征值组成的对角矩阵。如果WWW由标准正交基组成,则W−1WTW^{-1}W^TW−1WT,特征分解可进一步写成WTΣWW^T\Sigma WWTΣ…...
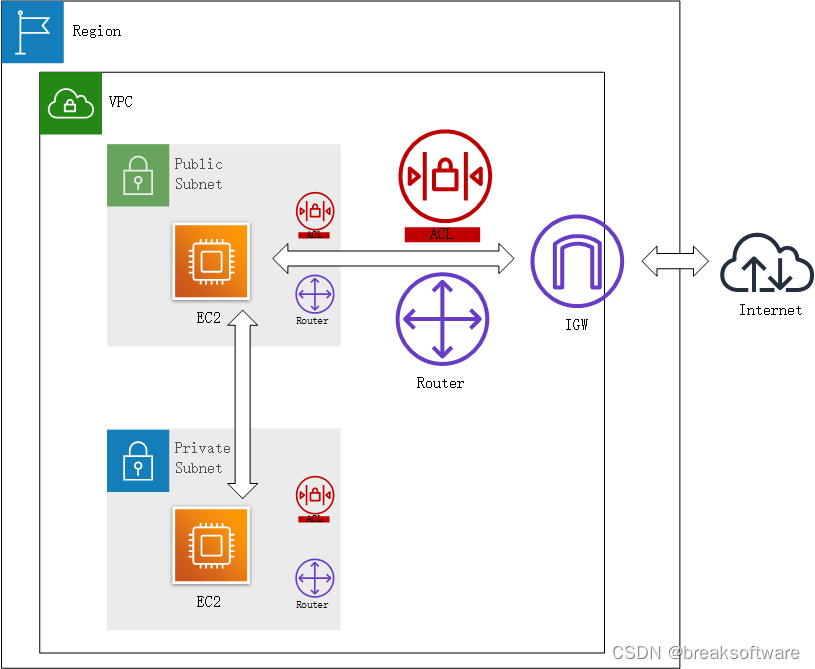
AWS攻略——子网
文章目录分配子网给Public子网分配互联网网关创建互联网网关附加到VPC给Public子网创建路由表关联子网打通Public子网和互联网网关创建Public子网下的EC2进行测试配置Private子网路由给Private子网创建路由表附加在Private子网创建Private子网下的EC2进行测试创建实例在跳板机上…...

java面试 - mq
RocketMq和RabbitMq的优缺点 1、RabbitMQ 优点:rabbitMq 几万级数据量,基于erlang语言开发,因此响应速度快些,并且社区活跃度比较活跃,可视化界面。 缺点:数据吞吐量相对与小一些,并且是基于er…...
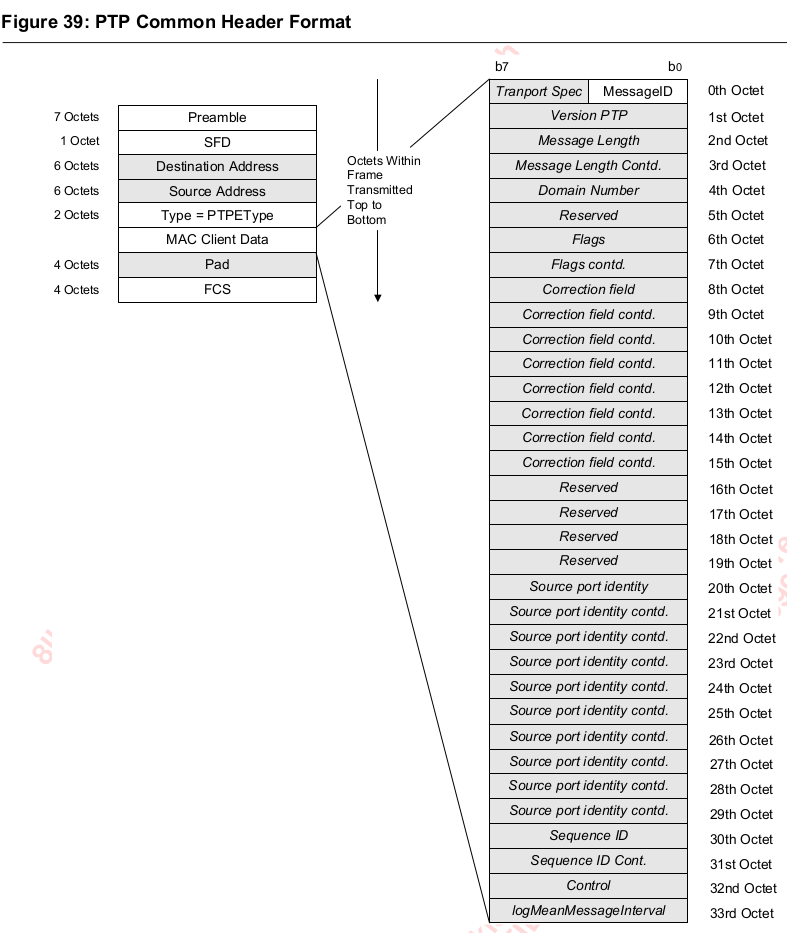
PTP GPTP芯片资料翻译88E6352
88E6352应用 网关 车载信息娱乐 车身域控制器 PTP PTP通过周期型地交换控制包实现 选择其中网络最佳质量时钟元素,作为PTP网络中Grand Master.没有Grand Master 节点变成PTP slave节点。PTP节点从Grand Master节点获得他们驱动频率和时间信息。 基本观念是PTP帧…...
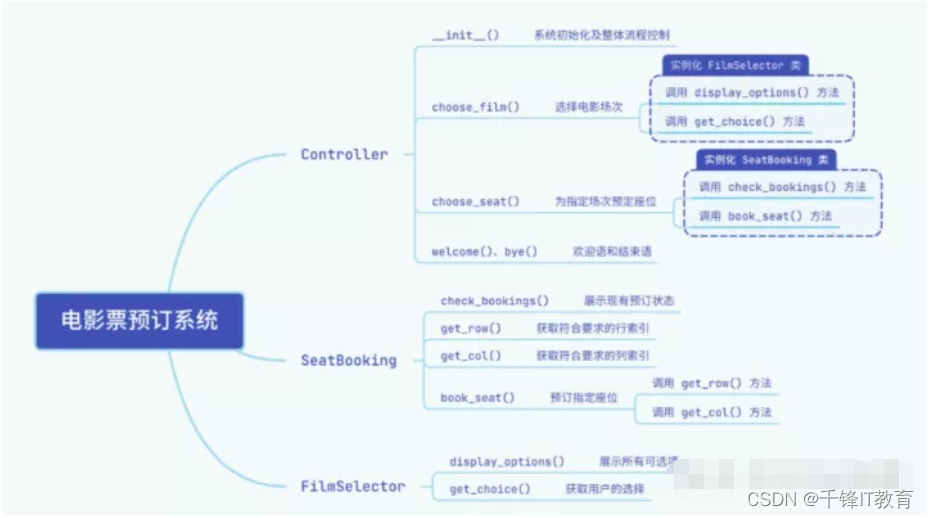
用Python实现一个电影订票系统
一、效果展示通过Python实现一个电影订票系统,效果如下所示:二、整体结构图三、代码分解3.1 infos.py一部电影的详细信息适合用 字典 结构来存储,我们可以给字典里添加多个键值对来保存电影的名称、座位表和宣传时用的字符画,比如…...

什么是瞪铃企业
“瞪羚企业”是指创业后跨过死亡谷以科技创新或商业模式创新为支撑进入高成长期的中小企业。认定范围主要是产业领域符合国家和省战略新兴产业发展方向,涵盖新兴工业、新一代信息技术、生物健康、人工智能、金融科技、节能环保、消费升级等领域。按照硅谷的解释&…...
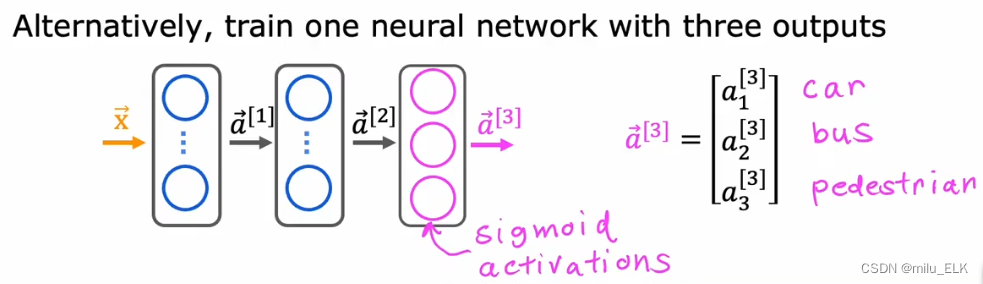
【深度学习】多分类问题和多标签分类问题
上一章——激活函数 文章目录什么是多分类问题Softmax贝叶斯公式softmax的损失函数多标签分类问题什么是多分类问题 在之前的课程中,我们学习了二分问题,二分问题中的所有数据会被分类为0和1(或者Ture和False)两种输出标签。但是…...

大学生开学买什么,返校必备数码好物推荐
开学还不知道需要准备些什么,这篇开学数码好物,希望能够对你在开学购买的好物有一些帮助,一款好的数码装备,可以让我们在学校学习当中能够用最少的时间,最大的产出,节省时间,提高学习效率&#…...
Unreal Engine06:Actor的实现
写在前面 Actor是可以放进地图的最基本类,这里主要是介绍一下Actor的使用。 一、空间坐标系 1. Actor的变换操作 Actor的变换变换操作主要包括四个部分: 位置;旋转;缩放; 上面三者都是对应三个轴进行变换࿱…...
2023美国大学生数学建模竞赛C题思路解析(含代码+数据可视化)
以下为2023美国大学生数学建模竞赛C题思路解析(含代码数据可视化)规则:猜词,字母猜对,位置不对为黄色,位置对为绿色,两者皆不对为灰色。困难模式下的要求:对于猜对的字母(…...
aws codebuild 自定义构建环境和本地构建
参考资料 Extending AWS CodeBuild with Custom Build Environments Docker in custom image sample for CodeBuild codebuild自定义构建环境 在创建codebuild项目的时候发现 构建环境是 Docker 映像,其中包含构建和测试项目所需的所有内容的完整文件系统 用ru…...
3年功能3年自动化,从8k到23k的学习过程
简单的先说一下,坐标杭州,14届本科毕业,算上年前在阿里巴巴的面试,一共有面试了有6家公司(因为不想请假,因此只是每个晚上去其他公司面试,所以面试的公司比较少)其中成功的有4家&…...

leaflet: 数据聚合,显示当前bounds区域中的点的名称列表(078)
第078个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中实现数据聚合的功能 ,左边列出右边可视区域内的marker的名称。这里主要用到了可视区域的范围以及contains函数。 直接复制下面的 vue+leaflet源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方…...
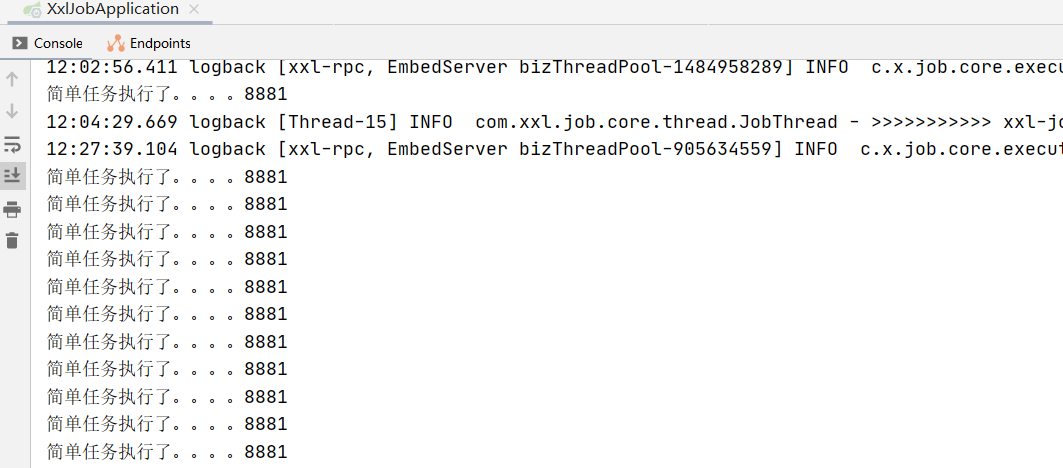
XXL-JOB分布式任务调度框架(一)-基础入门
文章目录1.什么是任务调度2.常见定时任务方案2.1. 传统定时任务方案示例2.2. 缺点分析3.什么是分布式任务调度?3.1. 并行任务调度3.2. 高可用3.3. 弹性扩容3.4. 任务管理与监测4.市面上常见的分布式任务调度产品5.初识xxl-job6.xxl-job架构设计6.1.设计思想6.2.架构…...

基于CentOS 7 搭建Redis 7集群
我们的目标是使用2台(多台服务器类似)服务器搭建一个3主3从的redis集群。 我们为什么要使用redis 7呢?因为6、7的版本都做了大量优化,比如6引入了多线程(一些JAVA八股文面试还喜欢问redis为什么是单线程)&…...

Lesson5.3---Python 之 NumPy 统计函数、数据类型和文件操作
一、统计函数 NumPy 能方便地求出统计学常见的描述性统计量。最开始呢,我们还是先导入 numpy。 import numpy as np1. 求平均值 mean() mean() 是默认求出数组内所有元素的平均值。我们使用 np.arange(20).reshape((4,5)) 生成一个初始值默认为 0,终止…...
Puppeteer 爬虫学习
puppeteer简介: Puppeteer 是一个 Node 库,它提供了一个高级 API 来通过 DevTools 协议 控制 Chromium 或 Chrome。Puppeteer 默认以 headless 模式运行, 但是可以通过修改配置文件运行“有头”模式。能作什么?: 生成…...
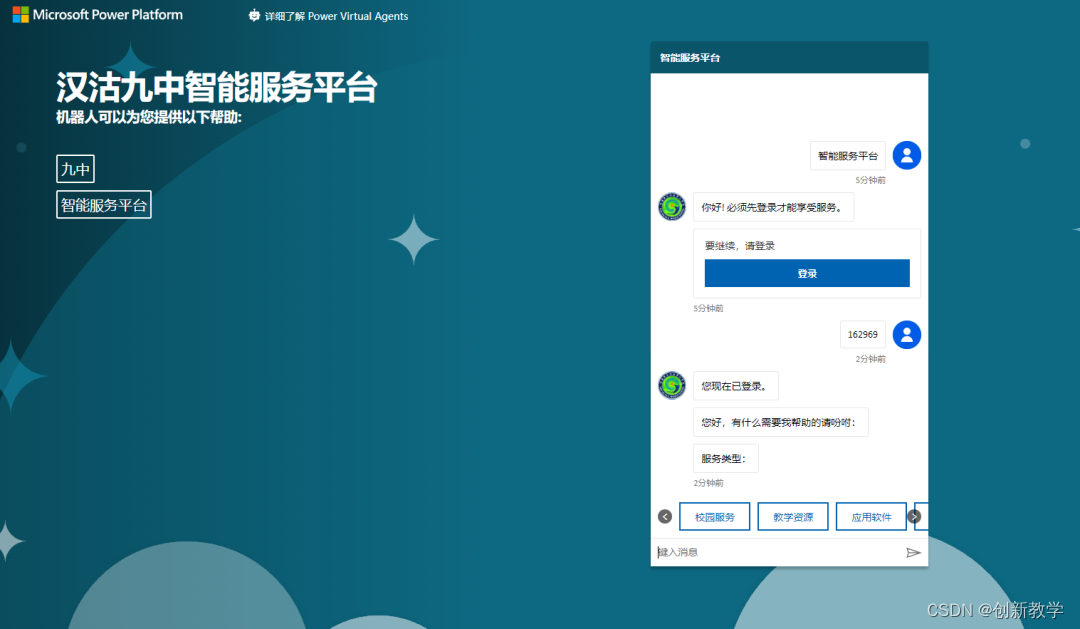
如何在Power Virtual Agents中实现身份验证
今天我们介绍一下如何通过身份验证的方式来使用Power Virtual Agents。首先进入“Microsoft 365-管理-Azure Active Directory管理中心”。 进入“Azure Active Directory管理中心”后选择“Azure Active Directory”中的“应用注册”-“新注册”。 输入新创建的应用程序名称后…...

金三银四必备软件测试必问面试题
初级软件测试必问面试题1、你的测试职业发展是什么?测试经验越多,测试能力越高。所以我的职业发展是需要时间积累的,一步步向着高级测试工程师奔去。而且我也有初步的职业规划,前 3 年积累测试经验,按如何做好测试工程…...
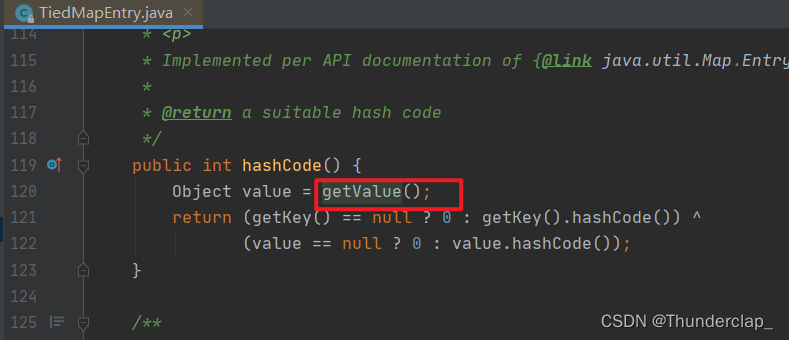
Java反序列化漏洞——CommonsCollections6链分析
一、前因因为在jdk8u71之后的版本中,sun.reflect.annotation.AnnotationInvocationHandler#readObject的逻辑发生了变化,导致CC1中的两个链条都不能使用,所有我们需要找一个在高版本中也可用的链条。/* Gadget chain: java.io.ObjectInputStr…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
