如何从第一性原则的原理分解数学问题
如何从第一性原则的原理分解数学问题
摘要:牛津大学入学考试题目展示了所有优秀数学家都使用的系统的第一原则推理,而GPT4仍然在这方面有困难
作者:Keith McNulty
我们中的许多人都熟悉直角三角形的边的规则。根据毕达哥拉斯定理,如果a和b是两条较短的边,c是最长的边,那么a² + b² = c²。
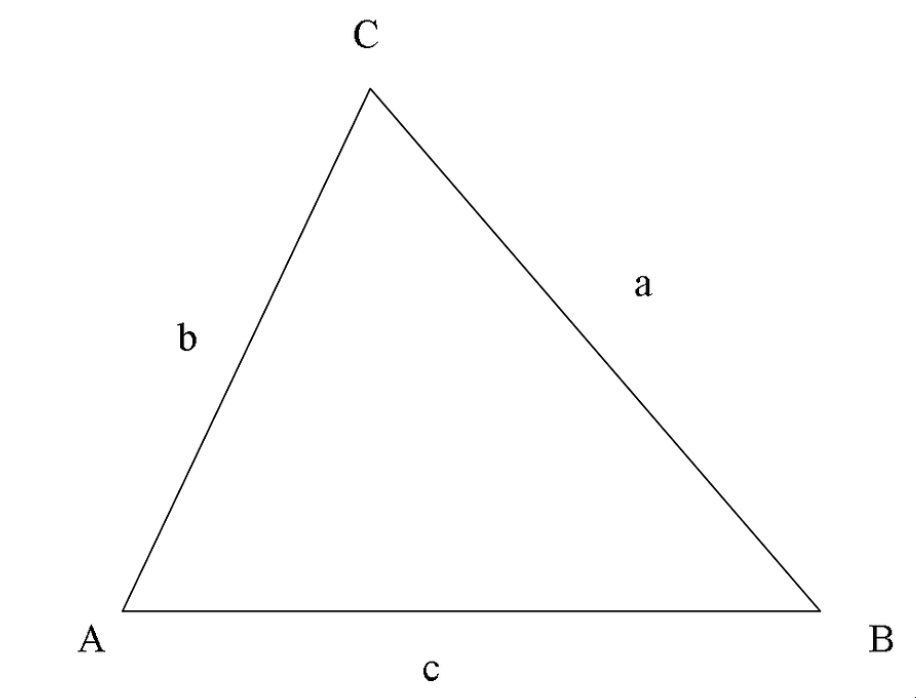
已知的整数解称为毕达哥拉斯三元组。例如,(3, 4, 5) 和 (5, 12, 13) 就是其中的一些。
更一般的构造是三元组。任何一组可以构成三角形的正整数三元组都称为三元组。
显然,整数毕达哥拉斯三元组也是三元组。但通常情况下,如果一个整数三元组 (a, b, c) 在(非严格)递增的顺序列出时,前两个整数的和严格大于第三个整数,那么它就是一个三元组。
以 (4, 2, 3) 为例。这些可以是三角形的边长,因为2 + 3 > 4。类似地,(2, 2, 2) 是一个三元组。但 (1, 3, 1) 不是三元组,因为无法用这些边长构建三角形(1 + 1 ≯ 3)。
最近牛津大学入学考试的一个问题涉及到三元组,我认为它很好地说明了如何逐步从第一原则分解问题,以解决起初看起来非常具有挑战性的问题。
这个问题定义了一个函数 f(P),其中 P > 2,表示三元组的数量,它们的和为 P。最后,它要求我们找到 f(21)。
找到和为 21 的三元组的数量似乎是一个真正的智力挑战,但是使用一些逐步的系统步骤,我们可以找到一个非常简单的计算方法。
最后,我还将展示像GPT4这样的人工智能在需要第一原则推理的这类问题上存在真正的问题。
以下是问题的各个部分和我的解决方案。我发现这是一个有趣的问题,是数学思维的很好练习,几乎不需要课本知识。
(i) 找到 f(3), f(4), f(5), f(6) 的值 这只是让我们适应思考和理解一个新概念。
由于唯一的正整数三元组,其和为三,是 (1, 1, 1),而且这显然是一个三元组,所以 f(3) = 1
任何和为 4 的正整数三元组都必须包含2。因此,另外两个数字都是1。由于1 + 1 不严格大于 2,所以不存在三元组,因此 f(4) = 0。
任何和为 5 的正整数三元组都必须包含2或3,但不能同时包含。如果它包含3,那么其他两个必须都是1,而这不是三元组。如果它包含2,那么其他两个必须是1和2,这是一个三元组。
因此,(2, 2, 1),(2, 1, 2) 和 (1, 2, 2) 都是这样的三元组,所以 f(5) = 3。
任何和为 6 的正整数三元组必须包含一个4和两个1(不是三元组),一个3、2和1各一个(不是三元组),或者三个2(是三元组)。
因此,唯一的三元组是 (2, 2, 2),因此 f(6) = 1。
(ii) 如果 (a, b, c) 是一个三元组,证明 (a+1, b+1, c+1) 也是一个三元组
首先注意,我们总是可以假设 a, b, c 是(非严格)递增的顺序,因为如果它们不是,我们可以简单地重新排列它们,使它们变成递增的。
这种推理在这个问题的大多数部分都很重要。
现在,由于 a+b > c,我们可以说 (a+1) + (b+1) = (a+b)+2 > c+2 > c+1。因此,(a+1, b+1, c+1) 是一个三元组。
(iii) 如果 (x, y, z) 是一个三元组,x+y+z 是偶数且不小于 6,证明 x, y 和 z 都至少为 2,并且 (x-1, y-1, z-1) 也是一个三元组
再次假设 x, y, z 是递增的。为了证明它们都至少为 2,我们只需要证明 x 不能为 1。假设 x = 1。然后 1+y+z 是偶数,所以 y+z 是奇数。
此外,我们有 1+y > z,所以 y > z -1,因此 y ≥ z。但我们知道 y ≤ z,因此 y = z。所以 y+z 是偶数。
这是一个矛盾,所以 x > 1。
(iv) 证明对于任何大于等于 3 的正整数 k,f(2k-3) = f(2k) 根据第二部分,我们知
道任何和为 2k-3 的三元组都可以通过简单地对每个整数加 1 映射到和为 2k 的三元组。
这意味着和为 2k 的三元组集合至少和和为 2k-3 的三元组集合一样大。
根据第三部分,由于 2k 是偶数且不小于 6,我们知道我们可以通过从每个整数中减去 1 来将和为 2k 的三元组唯一映射到和为 2k-3 的三元组。
这意味着和为 2k-3 的三元组集合至少和和为 2k 的三元组集合一样大。
因此,两个集合必须具有相同的大小,因此 f(2k-3) = f(2k)。
(v) 设 S ≥ 3,令 P = 2S。证明 (a, b, c) 是和为 P 的三元组,如果且仅如果 a, b, c 中的每一个都严格小于 S
这是一个“如果且仅如果”的证明,所以我需要在两个方向上证明它。
再次假设 a, b, c 是递增的,并且它们的和为 P。
首先,我们需要证明如果 a+b > c,那么 c < S。假设 c ≥ S。然后 a+b > c ≥ S,所以 a+b+c > 2S = P。这是一个矛盾,所以 c < S。
现在我们需要证明如果 c < S,那么 a+b > c。如果 c < S,那么 2S-c > S > c。但是 a+b+c = P = 2S,所以 a+b = 2S-c。因此 a+b > c。
(vi) 对于任何 2 ≤ a ≤ S-1,证明使得 (a, b, P-a-b) 成为一个三元组的可能值的 b 的数量为 a-1
根据第五部分,P-a-b = 2S-a-b ≤ S-1。所以 S-a+1 ≤ b。但同时 b ≤ S-1。因此,对于任何特定的 a 值,b 的值可以在 S-a+1 到 S-1 之间变化。
因此,可能的 b 的总数是 (S-1)-(S-a) = a-1。
(vii) 找到任何大于等于 6 的偶数 P 的 f(P) 的表达式
让 (a, b, P-a-b) 是和为 P 的三元组,其中 P 是偶数且不小于 6。根据第三部分和第五部分,我们知道 a 可以从 2 变到 S - 1,而根据第六部分,对于每个这样的 a 值,都有 a-1 个 b 值。
所以我们的 f(P) 的表达式可以如下推导:
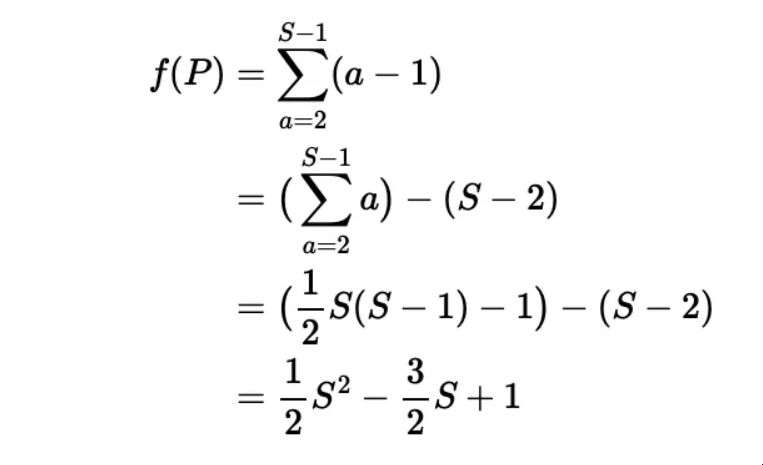
(viii) 找到 f(21)
根据第四部分,f(21) = f(24)。由于 24 是偶数且大于 6,我们可以使用第七部分的新公式,取 S = 12,得到答案是 55。
让我们使用Python 和 R 中的一个简单计数函数来双重检查:
Python
def n_triangular_triples(P):
check = []
for a in range(1, P + 1):
for b in range(1, P - a + 1):
if P - a - b > 0:
sorted_triplet = sorted([a, b, P - a - b])
if sum(sorted_triplet) == P and sorted_triplet[0] + sorted_triplet[1] > sorted_triplet[2]:
check.append(1)
return sum(check)
# 测试 P = 21
result = n_triangular_triples(21)
print(result)
R
# 简单计算和为 P 的三元组的函数
n_triangular_triples <- function(P) {
check <- c()
for (a in 1:P) {
for (b in 1:(P - a)) {
if (P - a - b > 0) {
sorted <- sort(c(a, b, P - a - b))
if ((sum(sorted) == P) && (sorted[1] + sorted[2] > sorted[3])) {
check <- append(check, 1)
}
}
}
}
sum(check)
}
# 测试 P = 21
n_triangular_triples(21)
[1] 55
当然,我们还可以使用我们的新公式来计算更大的 P 的 f(P)。
例如,f(997) = f(1000) = 124,251。
我们可以使用 Python或R 中的函数来检查,如果您愿意等待几秒钟让它遍历所有可能的三元组。
n_triangular_triples(997)
[1] 124251
GPT4 在这方面的表现如何?
并不好,尽管它渴望解释三角不等式定理,但如下所示,它的表现并不理想。我提出了三次问题,得到的答案分别是 100、22 和 190。看来真正的智能没有替代品!
您对这个问题有何看法?欢迎发表评论。
本文由 mdnice 多平台发布
相关文章:
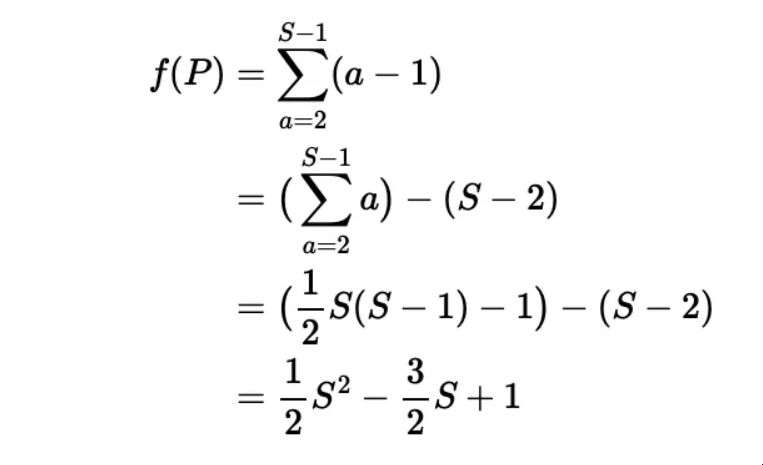
如何从第一性原则的原理分解数学问题
如何从第一性原则的原理分解数学问题 摘要:牛津大学入学考试题目展示了所有优秀数学家都使用的系统的第一原则推理,而GPT4仍然在这方面有困难 作者:Keith McNulty 我们中的许多人都熟悉直角三角形的边的规则。根据毕达哥拉斯定理,…...

实现strstr函数
一个字符串有没有在另一个字符串出现过 char* my_strstr(char* arr1, char* arr2) {char* cp;char* a1;char* a2;cp arr1;while (*cp){a1 cp;a2 arr2;while (*a1 *a2){a1;a2;}if (*a2 \0){return cp;}cp;}return NULL; } int main() {char arr1[] "abbbcdefgi"…...

C语言练习题解析(2)
💓博客主页:江池俊的博客⏩收录专栏:C语言刷题专栏👉专栏推荐:✅C语言初阶之路 ✅C语言进阶之路💻代码仓库:江池俊的代码仓库🎉欢迎大家点赞👍评论📝收藏⭐ 文…...
Element UI 表单验证规则动态失效问题
Element 版本:v2.15.3 问题背景 如下代码所示:有一个上传文件的 input 组件,在更新的时候,如果不上传文件表示不更新,如果要更新则点击 「重新上传」按钮将上传组件显示出来 <el-form ref"form" :mode…...
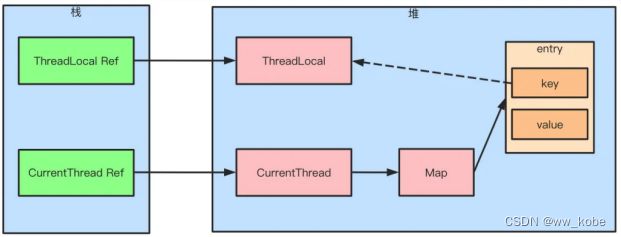
多线程并发篇
目录 1、线程生命周期 2、线程创建方式 3、Callable 与 Future 4、如何停止一个正在运行的线程 5、notify() 和 notifyAll() 的区别 6、sleep() 和 wait() 的区别 7、start() 和 run() 的区别 8、interrupted 和 isInterruptedd 的区别 9、CyclicBarrier 和 Count…...

pycharm-2023.1 closing project window stuck
pycharm-2023.1 closing project window stuck 问题描述 pycharm 切换项目/重启,一直卡在 closing project 原因分析 PyCharm 2023.1 issue - closing project window stuck (PyPIPackageUtil.lambda$parsePyPIListFromWeb) 解决方案 升级 pycharm 到 2023.3py…...

tkinter编写的打开csdn程序
目录 鬼畜tkinter简介程序代码解析现成总结鬼畜 看看你每次打开CSDN: 1.开机 2.打开浏览器 3.打开CSDN 4.等待 5.完成 我: 1.开机 2.点击%%%按钮 3.等待 4.完成 简单了不知道多少倍 上面的纯属鬼畜,下面正文!!! tkinter tkinter是一个用于创建图形用户界面(GUI)的Py…...

Vue3.2组件如何封装,以弹窗组件的封装为例
以前一直想,每次封装一个弹窗组件的时候,一直特别复杂,父传子,子传父,各种来回绕,来回修改。 一直想如何才能更加简化,但是一直没时间,今天终于抽时间出来封装了一下 本次封装简化…...
每天10个小知识点)
Vue知识系列(5)每天10个小知识点
目录 系列文章目录Vue知识系列(1)每天10个小知识点Vue知识系列(2)每天10个小知识点Vue知识系列(3)每天10个小知识点Vue知识系列(4)每天10个小知识点 知识点41.vue常用基本指令有哪些…...
)
Java基础题08——数组(查找下标所对应的值)
给定一个整数数组,输入一个值 n ,输出 n *在数组中的下标 **(*如果不存在输出 -1 ) 如:int[] arr {3, 2, 1, 4, 5}; 1 输入: 3 输出: 0 2. 输入: 6 输出: -1 int[] arr new int[]{3, 2, 1, 4,…...

LinkedList 源码分析
LinkedList 是一个基于双向链表实现的集合类。 LinkedList 插入和删除元素的时间复杂度 头部插入/删除:只需要修改头结点的指针即可完成插入/删除操作,因此时间复杂度为 O(1)。尾部插入/删除:只需要修改尾结点的指针即可完成插入/删除操作…...
)
跑步锻炼(蓝桥杯)
跑步锻练 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小蓝每天都锻炼身体。 正常情况下,小蓝每天跑 1 千米。如果某天是周一或者月初(1 日),为了激励自己&#x…...

【SLAM】视觉SLAM简介
【SLAM】视觉SLAM简介 task04 主要了解了SLAM的主流框架,清楚VSALM中间接法与直接法的主要区别在什么地方,其各自的优势是什么,了解前端与后端的关系是什么 1.什么是SLAM 2.VSALM中间接法与直接法的主要区别在什么地方,其各自的…...
Visual Studio2019报错
1- Visual Studio2019报错 错误 MSB8036 找不到 Windows SDK 版本 10.0.19041.0的解决方法 小伙伴们在更新到Visual Studio2019后编译项目时可能遇到过这个错误:“ 错误 MSB8036 找不到 Windows SDK 版本 10.0.19041.0的解决方法”,但是我们明明安装了该…...

ffplay源码解析-PacketQueue队列
包队列架构位置 对应结构体源码 MyAVPacketList typedef struct MyAVPacketList {AVPacket pkt; //解封装后的数据struct MyAVPacketList *next; //下一个节点int serial; //播放序列 } MyAVPacketList;PacketQueue typedef struct PacketQueue {MyAVPacketList …...

Flowable主要API介绍
1. ProcessEngine 负责与各个服务进行交互和管理流程的整个生命周期。 方法描述getName()close()startExecutors()启动所有流程引擎中的执行器。执行器用于处理流程实例的执行,在引擎启动时,执行器会自动运行并处理待办任务和定时任务。getRepositorySe…...

TensorFlow与pytorch特定版本虚拟环境的安装
TensorFlow与Python的版本对应,注意,一定要选择对应的版本,否则会让你非常痛苦,折腾很久搞不清楚原因。 建议使用国内镜像源安装 没有GPU后缀的就表示是CPU版本的,不加版本就是最新 pip install tensorflow -i https:…...

【SpringMVC】拦截器JSR303的使用
【SpringMVC】拦截器&JSR303的使用 1.1 什么是JSR3031.2 为什么使用JSR3031.3 常用注解1.4 Validated与Valid区别1.5 JSR快速入门1.5.2 配置校验规则# 1.5.3 入门案例二、拦截器2.1 什么是拦截器2.2 拦截器与过滤器2.3 应用场景2.4 拦截器快速入门2.5.拦截器链2.6登录案列权…...

Java - LambdaQueryWrapper 的常用方法
1、查看项目中是否导入mybatisPlus的jar包 2、servie 层和实现类要集成mybatisPlus service 继承IService<> 实现类中要继承IService的实现类ServiceImpl<mapper,实体类> 3、如果想要mapper中的一些方法,mapper 要继承BaseMapper<实体类> 4、在实…...

Selenium常见问题解析
1、元素定位失败: 在使用Selenium自动化测试时,最常见的问题之一是无法正确地定位元素,这可能导致后续操作失败。解决方法包括使用不同的定位方式(如xpath、CSS selector、id等),等待页面加载完全后再进行…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
