LeetCode 424. Longest Repeating Character Replacement
LeetCode 424. Longest Repeating Character Replacement
https://leetcode.com/problems/longest-repeating-character-replacement/
题目描述
You are given a string s and an integer k. You can choose any character of the string and change it to any other uppercase English character. You can perform this operation at most k times.
Return the length of the longest substring containing the same letter you can get after performing the above operations.
思路
- 滑动窗口
- 用一个map记录窗口中每个字符出现的次数, 取名fre
- 用一个变量记录窗口中出现次数最多的字符的次数, 取名maxCount
- 如果窗口的长度减去出现次数最多的字符的次数大于k,那么就需要移动左指针,直到窗口的长度减去出现次数最多的字符的次数小于等于k
- 例如:s = “AABABBA”, k = 1, 当窗口为[0, 2]时,map中记录的字符出现的次数为{‘A’: 2, ‘B’: 1}, maxCount = 2, 此时窗口的长度减去出现次数最多的字符的次数为2(right) - 0(left) + 1 - 2(maxCount) = 1 == 1(k), 此时窗口的长度减去出现次数最多的字符的次数小于等于k, 不需要移动左指针
- 每次移动左指针时,需要将左指针指向的字符在map中的次数减1, left++
- 每次移动右指针时,需要将右指针指向的字符在map中的次数加1, right++
- 每次移动左指针或者右指针时,都需要更新maxCount, maxCount = max(maxCount, fre[s[right]])
数据结构
var (size = len(s) // s字符串的长度fre = make(map[byte]int, 26) // map记录窗口中每个字符出现的次数, 因为题目中说了只有大写字母,所以map的长度为26maxLen = 0 // 最长的子串的长度maxCount = 0 // 窗口中出现次数最多的字符的次数)
算法
func characterReplacement(s string, k int) int {for left, right := 0, 0; right < size; right++ {fre[s[right]]++ // 右指针指向的字符在map中的次数加1if maxCount < fre[s[right]] { // 更新maxCountmaxCount = fre[s[right]]}if right-left+1-maxCount > k { // 如果窗口的长度减去出现次数最多的字符的次数大于k,那么就需要移动左指针fre[s[left]]-- // 左指针指向的字符在map中的次数减1left++ // 窗口左指针右移}if maxLen < right-left+1 { // 更新maxLenmaxLen = right - left + 1}}return maxLen
}
相关文章:

LeetCode 424. Longest Repeating Character Replacement
LeetCode 424. Longest Repeating Character Replacement https://leetcode.com/problems/longest-repeating-character-replacement/ 题目描述 You are given a string s and an integer k. You can choose any character of the string and change it to any other upperc…...
建立自己的博客(记录-不推荐)
环境安装: w10系统安装 第一步:安装git Git 官网: https://git-scm.com/ 第二步:安装Node.js Node.js官网:https://nodejs.org/zh-cn/ 使用cmd检测: node -v 第三步:安装Hexo Hexo官网:htt…...
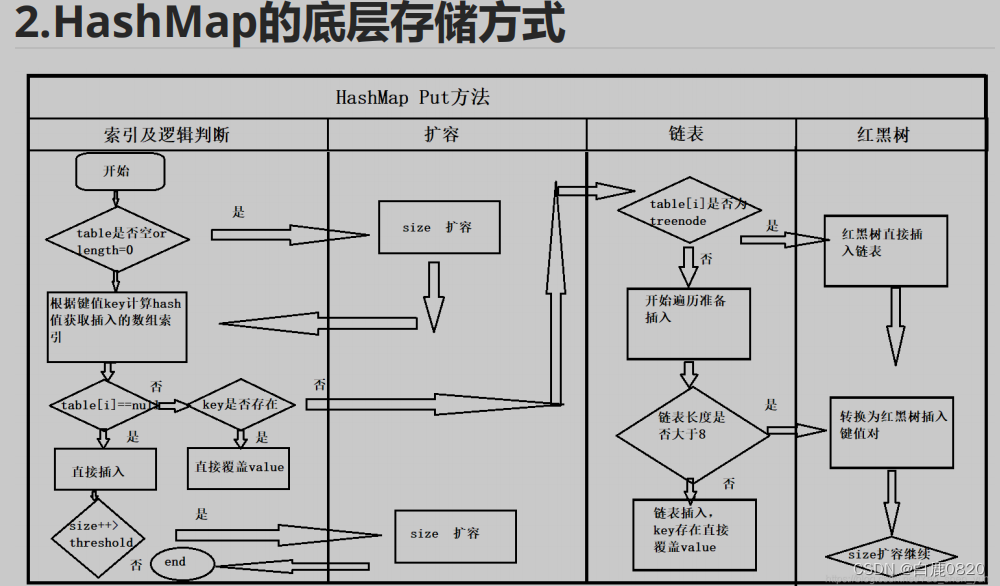
hashmap存储方式 hash碰撞及其解决方式
1.Map的存储特点 在Map这个结构中,数据是以键值对(key-value)的形式进行存储的,每一个存储进map的数据都是一一对应的。 创建一个Map结构可以使用new HashMap()以及new TreeMap()两种方式,两者之间的区别是:…...

Amazon GuardDuty 的新增功能 – Amazon EBS 卷的恶意软件检测
亚马逊云科技开发者社区为开发者们提供全球的开发技术资源。这里有技术文档、开发案例、技术专栏、培训视频、活动与竞赛等。帮助中国开发者对接世界最前沿技术,观点,和项目,并将中国优秀开发者或技术推荐给全球云社区。如果你还没有关注/收藏…...

YOLOv7 pytorch
yolov7主干部分结构图:yolov7主干 yolov7数据集处理代码:yolov7数据集处理代码 yolov7训练参数解释:yolov7训练参数【与本文代码有区别】 yolov7训练代码详解:yolov7训练代码详解 目录 训练自己的训练集 训练自己的训练集 此…...

JDK自带JVM分析工具
一、JDK自带工具盘点: jstat:性能分析-查看gc情况; jmap:内存分析-堆信息; jstack:线程分析-栈信息; jinfo:参数查看及配置; jstatd:启动jvm监控服务。它…...
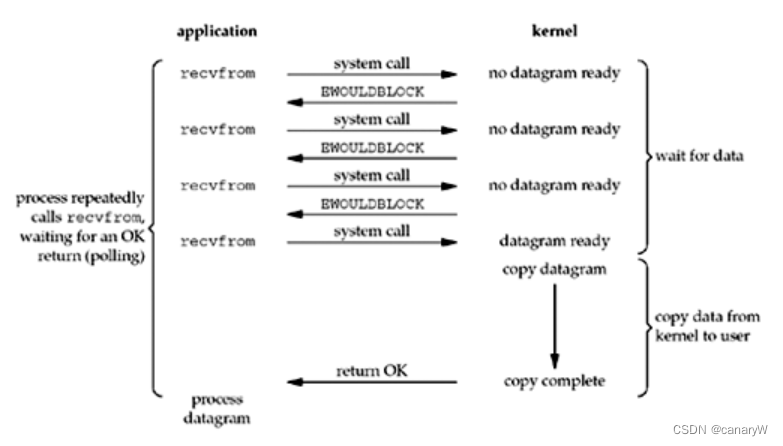
IO多路复用--[select | poll | epoll | Reactor]
因为在简历上写了netty的项目,因此还是将网络底层的那点东西搞清楚。 首先希望明确的是,BIO、NIO、IO多路复用这是不同的东西, 我会在本文中详细讲出来。 本文参考资料: JAVA IO模型 IO多路复用 select poll epoll介绍 从BIO到epo…...

pod的requests、limits解读、LimitRange资源配额、Qos服务质量等级、资源配额管理 Resource Quotas
前言 环境:k8s-v1.22.17 docker-20.10.9 centos-7.9 目录前言什么是可计算资源CPU、Memory计量单位pod资源请求、限额方式pod定义requests、limits查看节点资源情况pod使用request、limits示例LimitRange限制命名空间下的pod的资源配额Qos服务质量等级资源配额管理…...
:函数)
R语言基础(六):函数
R语言基础(一):注释、变量 R语言基础(二):常用函数 R语言基础(三):运算 R语言基础(四):数据类型 R语言基础(五):流程控制语句 7. 函数 函数是一组完成特定功能的语句。 7.1 内置函数 R语言系统中提供许多内置函数&…...

[C++] 简单序列化
前言 序列化(Serialization) 是将对象的状态信息转换为可以存储或传输的形式的过程。在序列化期间,对象将其当前状态写入到临时或持久性存储区。以后,可以通过从存储区中读取或反序列化对象的状态,重新创建该对象。 使用 序列化 std::array&…...
SomeIP之配置TCP/IP)
Autosar Configuration(十三)SomeIP之配置TCP/IP
本系列教程是根据实际项目开发中总结的经验所得,如发现有不对的地方,还请指正。 目录Autosar Configuration(一)Davinci Developer-工具介绍 Autosar Configuration(二)Davinci Developer-SWC配置 Autosar Configuration(三) Security之Crypto配置 Autosar Configurat…...

滤波算法 | 无迹卡尔曼滤波(UKF)算法及其Python实现
文章目录简介UKF滤波1. 概述和流程2. Python代码第一个版本a. KF滤波b. UKF滤波第二个版本简介 上一篇文章,我们介绍了UKF滤波公式及其MATLAB代码。在做视觉测量的过程中,基于OpenCV的开发包比较多,因此我们将UKF的MATLAB代码转到python中&a…...

IMU 积分的误差状态空间方程推导
文章目录0. 前言1. 离散时间的IMU运动学方程2. 状态变量定义3. 补充公式4. IMU误差状态空间方程推导4.1. 旋转误差 δr^i1\delta\hat{\mathbf{r}}_{i1}δr^i14.2. 速度误差 δv^i1\delta\hat{\mathbf{v}}_{i1}δv^i14.3. 平移误差 δpi1\delta \mathbf{p}_{i1}δpi14.4. …...

VirtualBox的克隆与复制
快照太多,想整合成1个文件怎么办? 最近,我就遇到一个问题。快照太多了。比较占用空间怎么办? 错误做法 一开始,我是这么操作的,选中某个快照,然后选择删除…然后我登录虚拟机后,发…...

每天5分钟玩转机器学习算法:逆向概率的问题是什么?贝叶斯公式是如何解决的?
本文重点 前面我们已经知道了贝叶斯公式,以及贝叶斯公式在机器学习中的应用,那么贝叶斯公式究竟解决了一个什么样的问题呢?贝叶斯是为了解决逆向概率的问题。 正向的概率和逆向的概率 正向概率:假设袋子里面有N个白球,有M个黑球,你伸手一摸,那么问题就是你摸出黑球的概…...

游戏闲聊之游戏是怎么赚钱的
其实一般情况下不太爱写这种文章,简单说就一点,这个行业的人我惹不起。 1、外挂 所谓外挂,是指通过技术手段,提供辅助游戏的工具,方便玩家获得一些额外的能力; 这事我特意咨询过律师,外挂分两…...
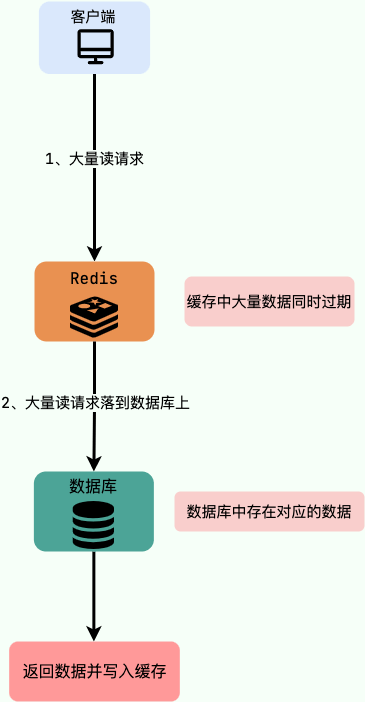
Redis高频面试题汇总(下)
目录 1.Redis中什么是Big Key(大key) 2.Big Key会导致什么问题 3.如何发现 bigkey? 4.为什么redis生产环境慎用keys *命令 5.如何处理大量 key 集中过期问题 6.使用批量操作减少网络传输 7.缓存穿透 8.缓存击穿 9.缓存雪崩 10.缓存污染(或满了…...
Windows修改Docker安装目录修改Docker镜像目录,镜像默认存储位置存放到其它盘
Windows安装Docker,默认是安装在C盘,下载镜像后会占用大量空间,这时需要调整镜像目录;场景:不想连服务器或者没有服务器,想在本地调试服务,该需求就非常重要。基于WSL2安装docker后,…...

376. 摆动序列——【Leetcode每日刷题】
376. 摆动序列 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。 例如, [1, 7, 4, 9, 2, 5] 是一个…...
mgre实验
实验思路 1、首先根据拓扑结构合理分配IP地址,并对各个路由器的IP地址和R5环回接口的IP地址进行配置。 2、让私网中的边界路由器对ISP路由器做缺省路由。 3、根据实验要求,对需要配置不同类型认证的路由器进行认证配置,和需要不同封装的协议…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
