Autosar Configuration(十三)SomeIP之配置TCP/IP
本系列教程是根据实际项目开发中总结的经验所得,如发现有不对的地方,还请指正。
目录
Autosar Configuration(一)Davinci Developer-工具介绍
Autosar Configuration(二)Davinci Developer-SWC配置
Autosar Configuration(三) Security之Crypto配置
Autosar Configuration(四) Security之CryIf配置
Autosar Configuration(五)
相关文章:
SomeIP之配置TCP/IP)
Autosar Configuration(十三)SomeIP之配置TCP/IP
本系列教程是根据实际项目开发中总结的经验所得,如发现有不对的地方,还请指正。 目录Autosar Configuration(一)Davinci Developer-工具介绍 Autosar Configuration(二)Davinci Developer-SWC配置 Autosar Configuration(三) Security之Crypto配置 Autosar Configurat…...

滤波算法 | 无迹卡尔曼滤波(UKF)算法及其Python实现
文章目录简介UKF滤波1. 概述和流程2. Python代码第一个版本a. KF滤波b. UKF滤波第二个版本简介 上一篇文章,我们介绍了UKF滤波公式及其MATLAB代码。在做视觉测量的过程中,基于OpenCV的开发包比较多,因此我们将UKF的MATLAB代码转到python中&a…...

IMU 积分的误差状态空间方程推导
文章目录0. 前言1. 离散时间的IMU运动学方程2. 状态变量定义3. 补充公式4. IMU误差状态空间方程推导4.1. 旋转误差 δr^i1\delta\hat{\mathbf{r}}_{i1}δr^i14.2. 速度误差 δv^i1\delta\hat{\mathbf{v}}_{i1}δv^i14.3. 平移误差 δpi1\delta \mathbf{p}_{i1}δpi14.4. …...

VirtualBox的克隆与复制
快照太多,想整合成1个文件怎么办? 最近,我就遇到一个问题。快照太多了。比较占用空间怎么办? 错误做法 一开始,我是这么操作的,选中某个快照,然后选择删除…然后我登录虚拟机后,发…...

每天5分钟玩转机器学习算法:逆向概率的问题是什么?贝叶斯公式是如何解决的?
本文重点 前面我们已经知道了贝叶斯公式,以及贝叶斯公式在机器学习中的应用,那么贝叶斯公式究竟解决了一个什么样的问题呢?贝叶斯是为了解决逆向概率的问题。 正向的概率和逆向的概率 正向概率:假设袋子里面有N个白球,有M个黑球,你伸手一摸,那么问题就是你摸出黑球的概…...

游戏闲聊之游戏是怎么赚钱的
其实一般情况下不太爱写这种文章,简单说就一点,这个行业的人我惹不起。 1、外挂 所谓外挂,是指通过技术手段,提供辅助游戏的工具,方便玩家获得一些额外的能力; 这事我特意咨询过律师,外挂分两…...
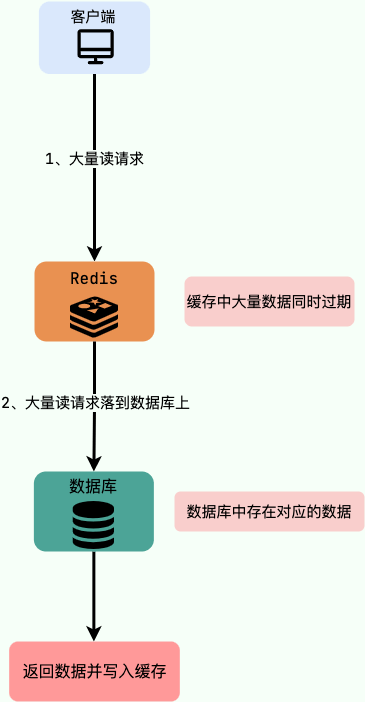
Redis高频面试题汇总(下)
目录 1.Redis中什么是Big Key(大key) 2.Big Key会导致什么问题 3.如何发现 bigkey? 4.为什么redis生产环境慎用keys *命令 5.如何处理大量 key 集中过期问题 6.使用批量操作减少网络传输 7.缓存穿透 8.缓存击穿 9.缓存雪崩 10.缓存污染(或满了…...
Windows修改Docker安装目录修改Docker镜像目录,镜像默认存储位置存放到其它盘
Windows安装Docker,默认是安装在C盘,下载镜像后会占用大量空间,这时需要调整镜像目录;场景:不想连服务器或者没有服务器,想在本地调试服务,该需求就非常重要。基于WSL2安装docker后,…...

376. 摆动序列——【Leetcode每日刷题】
376. 摆动序列 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。 例如, [1, 7, 4, 9, 2, 5] 是一个…...
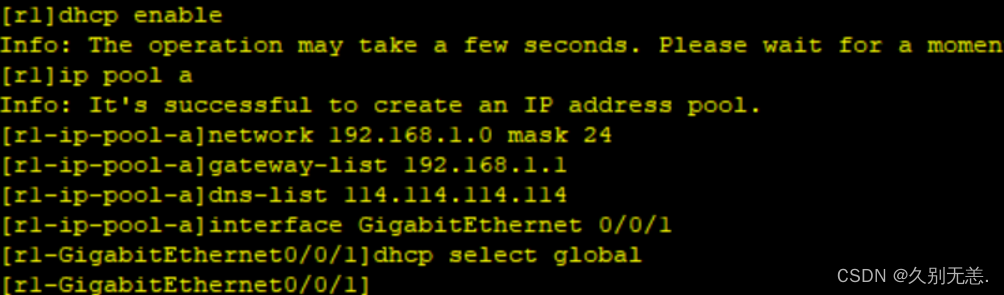
mgre实验
实验思路 1、首先根据拓扑结构合理分配IP地址,并对各个路由器的IP地址和R5环回接口的IP地址进行配置。 2、让私网中的边界路由器对ISP路由器做缺省路由。 3、根据实验要求,对需要配置不同类型认证的路由器进行认证配置,和需要不同封装的协议…...
)
一文彻底了解Zookeeper(介绍篇)
zookeeper 是什么? zookeeper是一个分布式协作框架,提供高可用,高性能,强一致等特性 zookeeper 有哪些应用场景? 分布式锁:分布式锁是指在分布式环境中,多个进程或线程需要互斥地访问某个共享…...
1. ELK Stack 理论篇之什么是ELK Stack?
ELK Stack 理论篇之什么是ELK Stack?1.1 什么是 ELK Stack?1.2 ELK Stack的发展史1.2.1 Elasticsearch1.2.2 引入 Logstash 和 Kibana,产品更强大1.2.3 社区越来越壮大,用例越来越丰富1.2.4 然后我们向 ELK 中加入了 Beats1.2.5 那么&#x…...
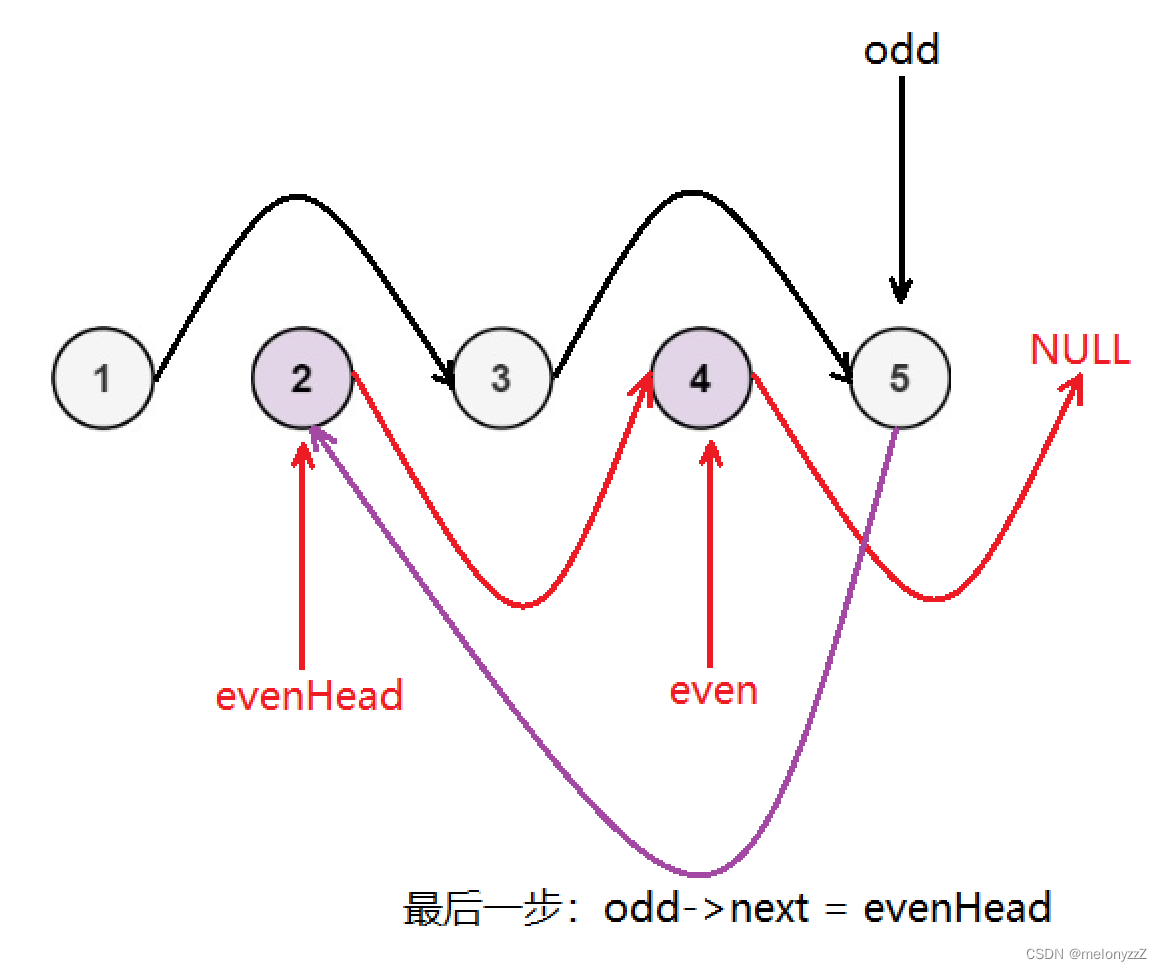
两道有关链表的练习
目录 一、分割链表 二、奇偶链表 一、分割链表 给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。 你不需要 保留 每个分区中各节点的初始相对位置。 示例 1: 输…...
Python uiautomator2安卓自动化测试
一、前言 uiautomator2是Python对Android设备进行UI自动化的库,支持USB和WIFI链接,可以实现获取屏幕上任意一个APP的任意一个控件属性,并对其进行任意操作。 重点是它可以实现安卓自动化采集,甚至是群控采集,且安装和…...

Leetcode. 160相交链表
文章目录指针解法指针解法 核心思路 : 先 分别求两个链表的长度 然后长的链表先走 差距步(长-短) 最后长链表和短链表同时走 ,第一地址相同的就是交点 ,注意一定是地址相同 不可能出现上图这种情况 ,因为C1…...

MDPs —— 马尔可夫决策定义与算法
文章目录MDPs 定义——由实例开始时序决策问题给游戏增点乐子*为什么要有折扣游戏的解——原则所以,什么是 MDPs?MDPs 的基本原理、表示光环原理效用的求解是反向传播的原则不变条件MDPs 的表示MDPs 求解效用迭代法缺点原则迭代法MDPs 定义——由实例开始…...
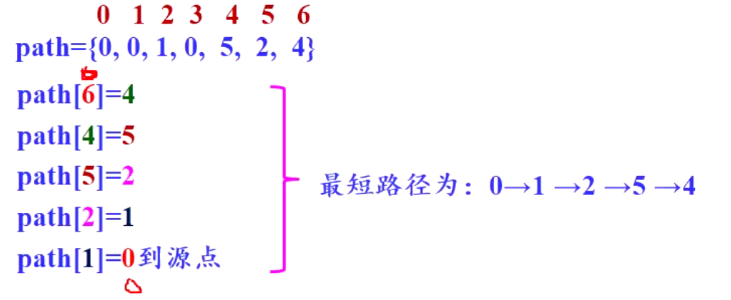
【C++】图
本文包含了图的基本概念 1.相关概念 1.1 无/有向 无向图:每一个顶点之间的连线没有方向 有向图:连线有方向(类似离散数学的二元关系 <A,B>代表从A到B的边,有方向) <A,B>中A为始点,B为终点在…...

尾递归优化
文章目录1. 前言2. 什么尾调用(Tail Call)?3. 尾调用优化4. Linux内核下的尾递归优化使用5. 参考资料1. 前言 限于作者能力水平,本文可能存在谬误,对此给读者带来的损失,作者不错任何承诺。 2. 什么尾调用…...

P1120 小木棍(搜索+剪枝)
题目链接:P1120 小木棍 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 9 5 2 1 5 2 1 5 2 1 样例输出: 6 分析:这道题一看数据范围就知道是搜索,但关键是需要剪枝。 首先我们求出所有木棍的长度和&am…...
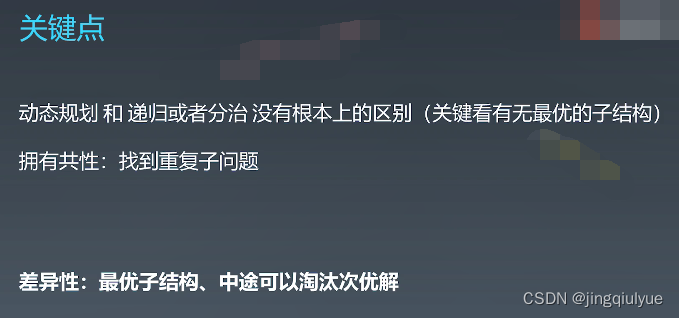
【专项训练】动态规划-3
动态规划:状态转移方程、找重复性和最优子结构 分治 + 记忆化搜索,可以过度到动态规划(动态递推) function DP():# DP状态定义# 需要经验,需把现实问题定义为一个数组,一维、二维、三维……dp =[][] # 二维情况for i = 0...M:...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
