R语言基础(六):函数
R语言基础(一):注释、变量
R语言基础(二):常用函数
R语言基础(三):运算
R语言基础(四):数据类型
R语言基础(五):流程控制语句
7. 函数
函数是一组完成特定功能的语句。
7.1 内置函数
R语言系统中提供许多内置函数,用户可以直接使用
> seq(1,5) #得到一个序列
[1] 1 2 3 4 5
> mean(2:8) #平均值
[1] 5
> x = c(-3,-1,1,2,3,4,5)
> mean(x,trim=0.2) #去除左右 20%的数据再计算
[1] 1.8
> median(x) #中位数
[1] 2
> max(22,33) #最大值
[1] 33R语言中包含常用的数学函数,比如四舍五入、对数函数、三角函数等。
7.2 自定义函数
自定义数使用function声明,函数声明包括参数(可选)和返回值(可选)
#没有参数的函数,f1是函数名
f1 <- function(){
for(i in 1:5){
print(i)
}
}
#调用函数
f1()
[1] 1
[1] 2
[1] 3
[1] 4
[1] 5
#有参数的函数,a是自定义的参数
f2 <- function(a){
for(i in 1:a){
print(i)
}
}
#调用函数,需要传参数
f2(3)
[1] 1
[1] 2
[1] 3
f2()
Error in f2() : 缺少参数"a",也没有缺省值
#带默认值的函数
f3 <- function(a=3,b=5){
for(i in a:b){
print(i)
}
}
f3(3,5)
[1] 3
[1] 4
[1] 5
#按参数名赋值
f3(b=5,a=2)
[1] 2
[1] 3
[1] 4
[1] 5
#有参数的函数,a是自定义的参数
f4 <- function(a,b){
sum=0
for(i in a:b){
sum=sum+i
}
#也可以直接写sum,省略return
return(sum)
}
s=f4(1,3) #调用并得到返回值
s
[1] 6
相关文章:
:函数)
R语言基础(六):函数
R语言基础(一):注释、变量 R语言基础(二):常用函数 R语言基础(三):运算 R语言基础(四):数据类型 R语言基础(五):流程控制语句 7. 函数 函数是一组完成特定功能的语句。 7.1 内置函数 R语言系统中提供许多内置函数&…...

[C++] 简单序列化
前言 序列化(Serialization) 是将对象的状态信息转换为可以存储或传输的形式的过程。在序列化期间,对象将其当前状态写入到临时或持久性存储区。以后,可以通过从存储区中读取或反序列化对象的状态,重新创建该对象。 使用 序列化 std::array&…...
SomeIP之配置TCP/IP)
Autosar Configuration(十三)SomeIP之配置TCP/IP
本系列教程是根据实际项目开发中总结的经验所得,如发现有不对的地方,还请指正。 目录Autosar Configuration(一)Davinci Developer-工具介绍 Autosar Configuration(二)Davinci Developer-SWC配置 Autosar Configuration(三) Security之Crypto配置 Autosar Configurat…...

滤波算法 | 无迹卡尔曼滤波(UKF)算法及其Python实现
文章目录简介UKF滤波1. 概述和流程2. Python代码第一个版本a. KF滤波b. UKF滤波第二个版本简介 上一篇文章,我们介绍了UKF滤波公式及其MATLAB代码。在做视觉测量的过程中,基于OpenCV的开发包比较多,因此我们将UKF的MATLAB代码转到python中&a…...

IMU 积分的误差状态空间方程推导
文章目录0. 前言1. 离散时间的IMU运动学方程2. 状态变量定义3. 补充公式4. IMU误差状态空间方程推导4.1. 旋转误差 δr^i1\delta\hat{\mathbf{r}}_{i1}δr^i14.2. 速度误差 δv^i1\delta\hat{\mathbf{v}}_{i1}δv^i14.3. 平移误差 δpi1\delta \mathbf{p}_{i1}δpi14.4. …...

VirtualBox的克隆与复制
快照太多,想整合成1个文件怎么办? 最近,我就遇到一个问题。快照太多了。比较占用空间怎么办? 错误做法 一开始,我是这么操作的,选中某个快照,然后选择删除…然后我登录虚拟机后,发…...

每天5分钟玩转机器学习算法:逆向概率的问题是什么?贝叶斯公式是如何解决的?
本文重点 前面我们已经知道了贝叶斯公式,以及贝叶斯公式在机器学习中的应用,那么贝叶斯公式究竟解决了一个什么样的问题呢?贝叶斯是为了解决逆向概率的问题。 正向的概率和逆向的概率 正向概率:假设袋子里面有N个白球,有M个黑球,你伸手一摸,那么问题就是你摸出黑球的概…...

游戏闲聊之游戏是怎么赚钱的
其实一般情况下不太爱写这种文章,简单说就一点,这个行业的人我惹不起。 1、外挂 所谓外挂,是指通过技术手段,提供辅助游戏的工具,方便玩家获得一些额外的能力; 这事我特意咨询过律师,外挂分两…...
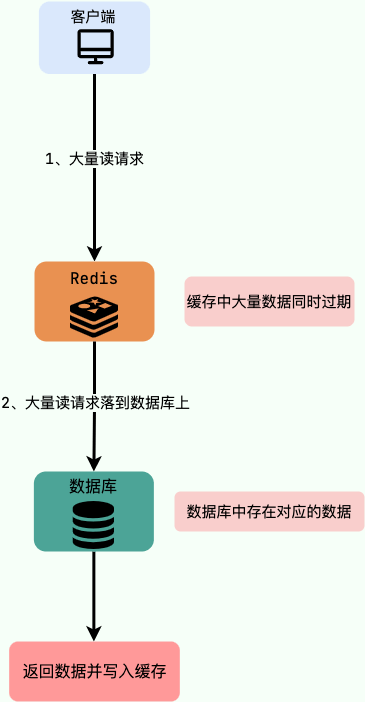
Redis高频面试题汇总(下)
目录 1.Redis中什么是Big Key(大key) 2.Big Key会导致什么问题 3.如何发现 bigkey? 4.为什么redis生产环境慎用keys *命令 5.如何处理大量 key 集中过期问题 6.使用批量操作减少网络传输 7.缓存穿透 8.缓存击穿 9.缓存雪崩 10.缓存污染(或满了…...
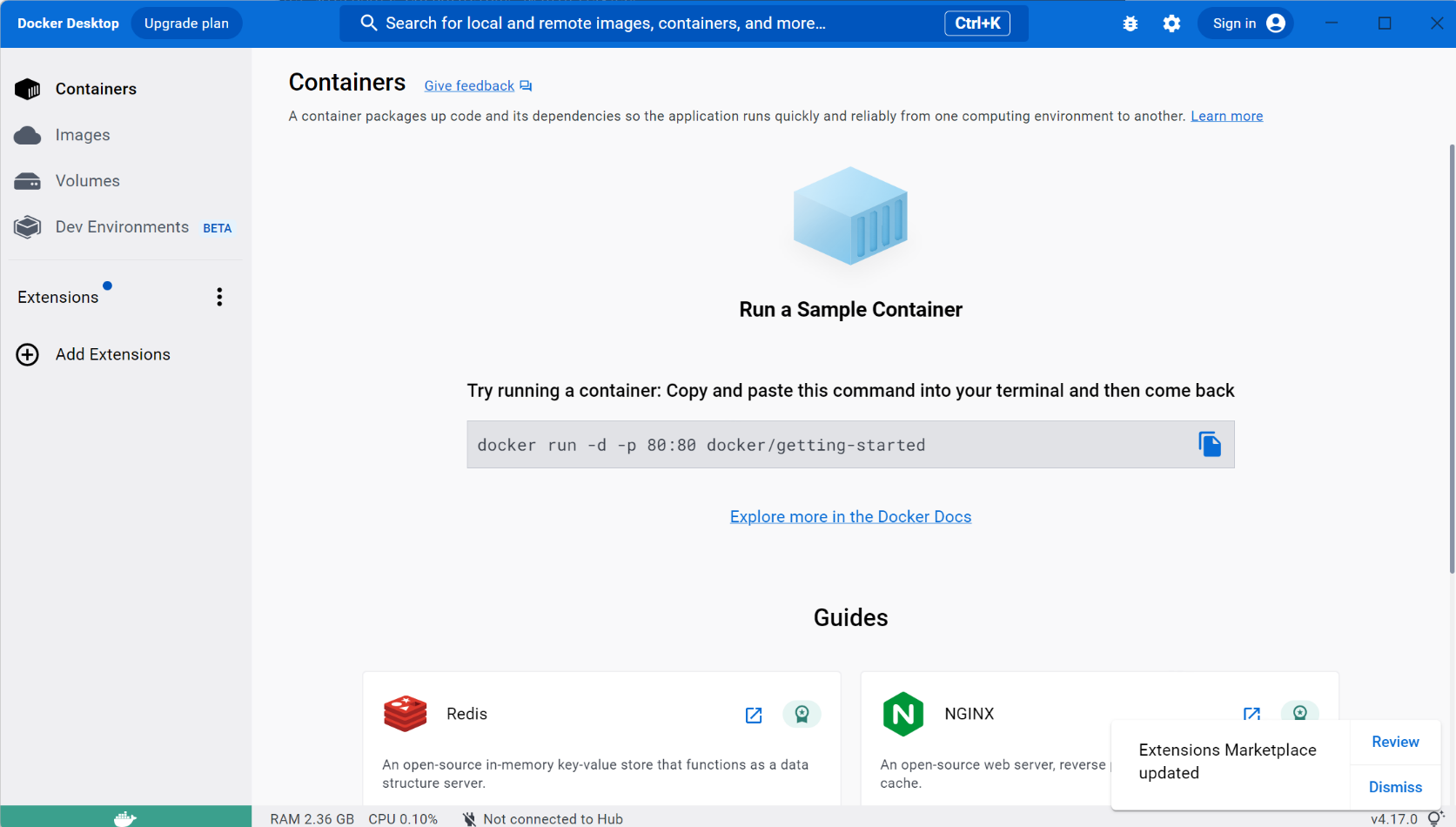
Windows修改Docker安装目录修改Docker镜像目录,镜像默认存储位置存放到其它盘
Windows安装Docker,默认是安装在C盘,下载镜像后会占用大量空间,这时需要调整镜像目录;场景:不想连服务器或者没有服务器,想在本地调试服务,该需求就非常重要。基于WSL2安装docker后,…...

376. 摆动序列——【Leetcode每日刷题】
376. 摆动序列 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。 例如, [1, 7, 4, 9, 2, 5] 是一个…...
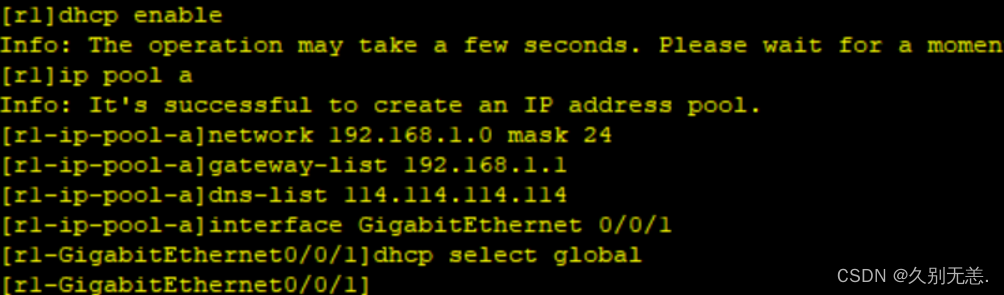
mgre实验
实验思路 1、首先根据拓扑结构合理分配IP地址,并对各个路由器的IP地址和R5环回接口的IP地址进行配置。 2、让私网中的边界路由器对ISP路由器做缺省路由。 3、根据实验要求,对需要配置不同类型认证的路由器进行认证配置,和需要不同封装的协议…...
)
一文彻底了解Zookeeper(介绍篇)
zookeeper 是什么? zookeeper是一个分布式协作框架,提供高可用,高性能,强一致等特性 zookeeper 有哪些应用场景? 分布式锁:分布式锁是指在分布式环境中,多个进程或线程需要互斥地访问某个共享…...
1. ELK Stack 理论篇之什么是ELK Stack?
ELK Stack 理论篇之什么是ELK Stack?1.1 什么是 ELK Stack?1.2 ELK Stack的发展史1.2.1 Elasticsearch1.2.2 引入 Logstash 和 Kibana,产品更强大1.2.3 社区越来越壮大,用例越来越丰富1.2.4 然后我们向 ELK 中加入了 Beats1.2.5 那么&#x…...
两道有关链表的练习
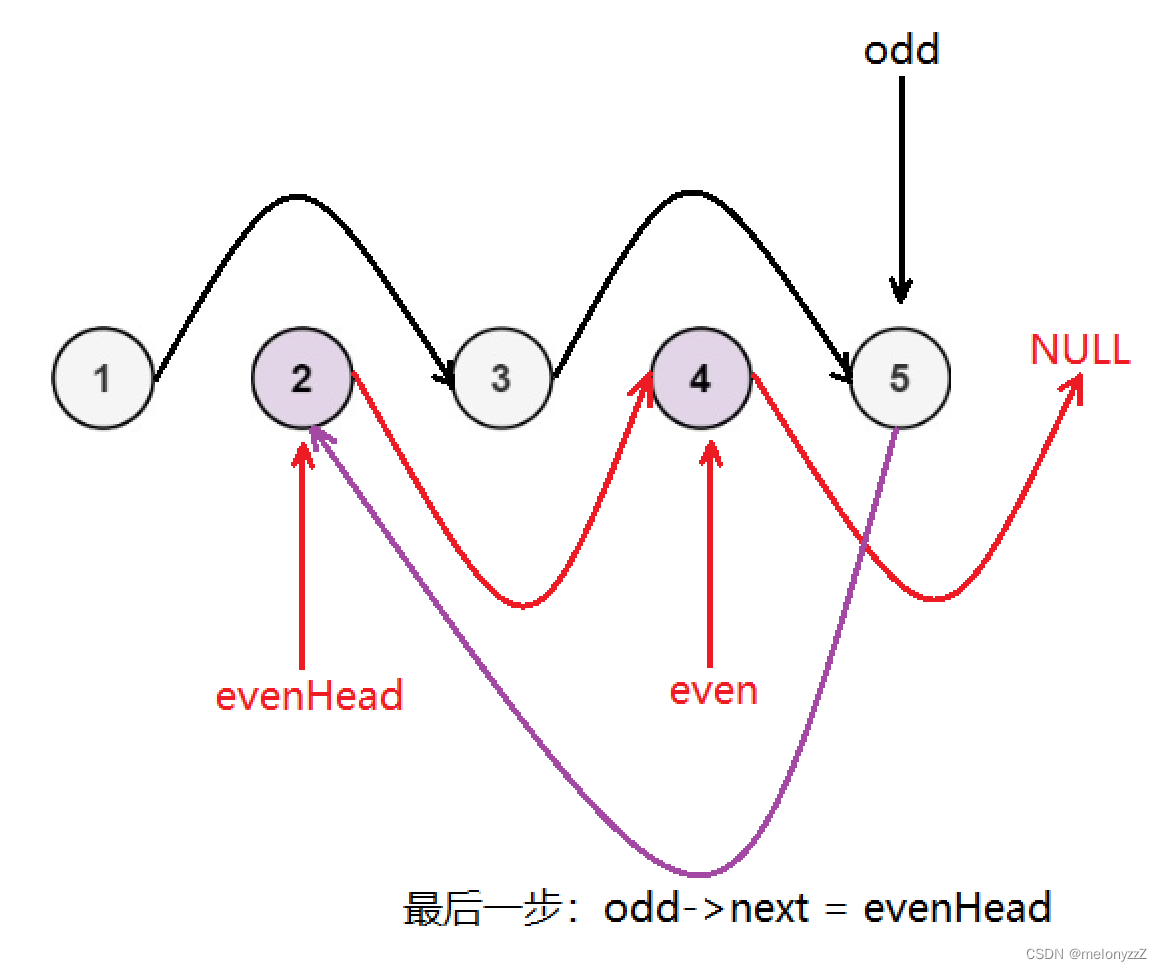
目录 一、分割链表 二、奇偶链表 一、分割链表 给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。 你不需要 保留 每个分区中各节点的初始相对位置。 示例 1: 输…...
Python uiautomator2安卓自动化测试
一、前言 uiautomator2是Python对Android设备进行UI自动化的库,支持USB和WIFI链接,可以实现获取屏幕上任意一个APP的任意一个控件属性,并对其进行任意操作。 重点是它可以实现安卓自动化采集,甚至是群控采集,且安装和…...

Leetcode. 160相交链表
文章目录指针解法指针解法 核心思路 : 先 分别求两个链表的长度 然后长的链表先走 差距步(长-短) 最后长链表和短链表同时走 ,第一地址相同的就是交点 ,注意一定是地址相同 不可能出现上图这种情况 ,因为C1…...

MDPs —— 马尔可夫决策定义与算法
文章目录MDPs 定义——由实例开始时序决策问题给游戏增点乐子*为什么要有折扣游戏的解——原则所以,什么是 MDPs?MDPs 的基本原理、表示光环原理效用的求解是反向传播的原则不变条件MDPs 的表示MDPs 求解效用迭代法缺点原则迭代法MDPs 定义——由实例开始…...
【C++】图
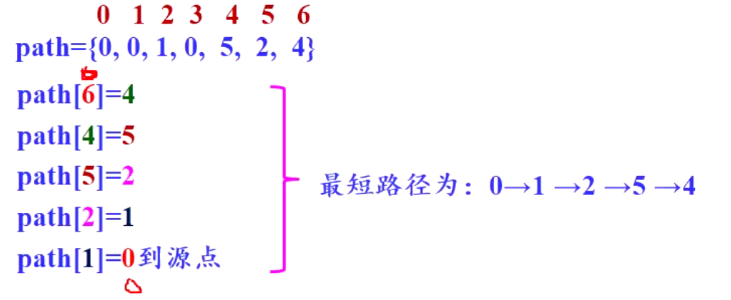
本文包含了图的基本概念 1.相关概念 1.1 无/有向 无向图:每一个顶点之间的连线没有方向 有向图:连线有方向(类似离散数学的二元关系 <A,B>代表从A到B的边,有方向) <A,B>中A为始点,B为终点在…...

尾递归优化
文章目录1. 前言2. 什么尾调用(Tail Call)?3. 尾调用优化4. Linux内核下的尾递归优化使用5. 参考资料1. 前言 限于作者能力水平,本文可能存在谬误,对此给读者带来的损失,作者不错任何承诺。 2. 什么尾调用…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
