应用层自定义协议与序列化
个人主页:Lei宝啊
愿所有美好如期而遇
协议
简单来说,就是通信双方约定好的结构化的数据。
序列化与反序列化
我们通过一个问题引入这个概念,假如我们要实现一个网络版的计算器,那么现在有两种方案,第一种,客户端发送一种类似于“1+1”这样的字符串,服务端接收到后进行拆解,然后计算。第二种,双方约定好一种结构体,按照某种规则转换成字符串发送给对方,然后对方再按照这种规则拆解成结构体,这个过程就叫做序列化与反序列化。

无论我们采用方案一, 还是方案二, 还是其他的方案, 只要保证, 一端发送时构造的数据,
在另一端能够正确的进行解析, 就是 ok 的. 这种约定, 就是 应用层协议。
理解Tcp为什么支持全双工
什么是全双工?简单来说,就是同时收发消息,而消息之间不会互相受到干扰。
具体来讲,全双工(Full Duplex)是一种通信方式,它允许数据在通信链路的两个方向上同时传输,即通信的双方可以同时发送和接收数据。

因为OS系统内部,Tcp为每一个连接的客户端维护了两个缓冲区,一个是发送缓冲区,一个是接收缓冲区,这样,就可以同时发送和接收信息而不互相干扰,read,write等系统调用在Tcp这里,也就支持了一个socketfd既可以读,也可以写。
Tcp粘包问题
TCP粘包是指发送方发送的若干包数据到接收方接收时粘成一包,从接收缓冲区看,后一包数据的头紧接着前一包数据的尾。这种现象既可能由发送方造成,也可能由接收方造成。
由于Tcp是基于字节流的协议,发送缓冲区内的数据什么时候发,发多少,出错了怎么办,完全由Tcp协议自己决定,所以就会导致出现报文发送不完整或者接收方不能读取完整报文的情况,那么接受方如果不对这种报文进行正确处理,就会导致粘包现象。
我们解决粘包问题的方案是,循环读入数据判断报文是否完整,如果完整则处理,并将缓冲区中的这段报文删除,判断处理下一个。
关于具体实现方案,我们后面的文章中,会给出具体实现。
相关文章:

应用层自定义协议与序列化
个人主页:Lei宝啊 愿所有美好如期而遇 协议 简单来说,就是通信双方约定好的结构化的数据。 序列化与反序列化 我们通过一个问题引入这个概念,假如我们要实现一个网络版的计算器,那么现在有两种方案,第一种&#x…...

Python学习笔记—100页Opencv详细讲解教程
目录 1 创建和显示窗口... - 4 - 2 加载显示图片... - 6 - 3 保存图片... - 7 - 4 视频采集... - 8 - 5视频录制... - 11 - 6 控制鼠标... - 12 - 7 TrackBar 控件... - 14 - 8.RGB和BGR颜色空间... - 16 - 9.HSV和HSL和YUV.. - 17 - 10 颜色空间的转化... - 18 - …...

C语言·分支和循环语句(超详细系列·全面总结)
前言:Hello大家好😘,我是心跳sy,为了更好地形成一个学习c语言的体系,最近将会更新关于c语言语法基础的知识,今天更新一下分支循环语句的知识点,我们一起来看看吧~ 目录 一、什么是语句…...

Gateway源码分析:路由Route、断言Predicate、Filter
文章目录 源码总流程图说明GateWayAutoConfigurationDispatcherHandlergetHandler()handleRequestWith()RouteToRequestUrlFilterReactiveLoadBalancerClientFilterNettyRoutingFilter 补充知识适配器模式 详细流程图 源码总流程图 在线总流程图 说明 Gateway的版本使用的是…...

ARM体系结构和接口技术(十)按键中断实验①
一、按键中断实验 (一)分析按键电路图 (二)芯片手册 二、按键中断实验分析 注:NVIC----Cortx-M核GIC----Cortx-A核 (一)查看所有外设的总线以及寄存器基地址 注:GIC的总线是A7核的…...

PostgreSQL使用(二)——插入、更新、删除数据
说明:本文介绍PostgreSQL的DML语言; 插入数据 -- 1.全字段插入,字段名可以省略 insert into tb_student values (1, 张三, 1990-01-01, 88.88);-- 2.部分字段插入,字段名必须写全 insert into tb_student (id, name) values (2,…...

有关css的题目
css样式来源有哪些? 内联样式: <a style"color: red"> </a> 内部样式:<style></style> 外部样式:写在独立的 .css文件中的 浏览器的默认样式 display有哪些属性 none - 不展示 block - 块类型…...

【开源库】libodb库编译及使用
前言 本文介绍windows平台下libodb库的编译及使用。 文末提供libodb-2.4.0编译好的msvc2019_64版本,可直接跳转自取 ODB库学习相关 【开源库学习】libodb库学习(一) 【开源库学习】libodb库学习(二) 【开源库学习】…...

电力需求预测挑战赛笔记 Task3 #Datawhale AI 夏令营
上文: 电力需求预测挑战赛笔记 Task2 #Datawhale AI 夏令营-CSDN博客文章浏览阅读80次。【代码】电力需求预测挑战赛笔记 Task2。https://blog.csdn.net/qq_23311271/article/details/140360632 前面我们介绍了如何使用经验模型以及常见的lightgbm决策树模型来解决…...

Promise 详解(原理篇)
目录 什么是 Promise 实现一个 Promise Promise 的声明 解决基本状态 添加 then 方法 解决异步实现 解决链式调用 完成 resolvePromise 函数 解决其他问题 添加 catch 方法 添加 finally 方法 添加 resolve、reject、race、all 等方法 如何验证我们的 Promise 是否…...

动态内存经典笔试题分析
目录 1.题目一 2.题目二 3.题目三 4.题目四 1.题目一 #include<stdlib.h> #include<stdio.h> #include<string.h> void GetMemory(char* p) {p (char*)malloc(100); } void Test(void) {char* str NULL;GetMemory(str);strcpy(str, "hello world…...
单例模式)
JS设计模式(一)单例模式
注释很详细,直接上代码 本文建立在已有JS面向对象基础的前提下,若无,请移步以下博客先行了解 JS面向对象(一)类与对象写法 特点和用途: 全局访问点:通过单例模式可以在整个应用程序中访问同一个…...

uniapp动态计算并设置元素高度
<template><view><scroll-view id"sv-box" :scroll-y"true" :style"{height:navHeightpx}"></scroll-view><view id"btn-box"><button>取消</button><button>确认</button><…...

直播架构如何设计核心节点和边缘节点
在直播架构中,核心节点和边缘节点的分工及主要服务是确保直播服务稳定、高效和可扩展的关键。以下是对这些节点的详细描述: 核心节点 核心节点通常位于数据中心,负责处理直播的主要逻辑和数据处理。其主要服务包括: 直播管理后…...
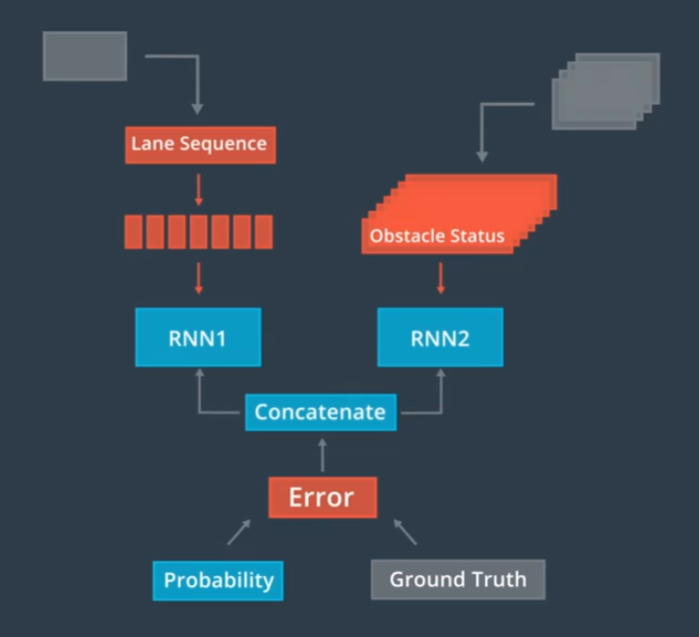
自动驾驶-预测概览
通过生成一条路径来预测一个物体的行为,在每一个时间段内,为每一辆汽车重新计算预测他们新生成的路径,这些预测路径为规划阶段做出决策提供了必要信息 预测路径有实时性的要求,预测模块能够学习新的行为。我们可以使用多源的数据…...

基于PSO算法优化PID参数的一些问题
目录 前言 Q1:惯性权重ω如何设置比较好?学习因子C1和C2如何设置? Q2:迭代速度边界设定一定能够遍历(/覆盖)整个PID参数二维空间范围吗?还是说需要与迭代次数相关?迭代次数越高&a…...

什么是决策树?
1. 什么是决策树? 决策树(Decision Tree)是一种常用的机器学习算法,用于解决分类和回归问题。它通过构建树结构来表示决策过程,分支节点表示特征选择,叶节点表示类别或回归值。 2. 决策树的组成部分 决策…...

ASP 快速参考
ASP 快速参考 概述 ASP(Active Server Pages)是一种由微软开发的服务器端脚本环境,用于动态网页设计和开发。它允许开发者创建和运行动态交互性网页,如访问数据库、发送电子邮件等。ASP页面通常以.asp为文件扩展名,并…...

(二)原生js案例之数码时钟计时
原生js实现的数字时间上下切换显示时间的效果,有参考相关设计,思路比较难,代码其实很简单 效果 代码实现 必要的样式 <style>* {padding: 0;margin: 0;}.content{/* text-align: center; */display: flex;align-items: center;justif…...

[CSS] 浮动布局的深入理解与应用
文章目录 浮动的简介元素浮动后的特点解决浮动产生的影响浮动后的影响解决浮动产生的影响 浮动相关属性实际应用示例示例1:图片与文字环绕示例2:多列布局示例3:响应式布局 总结 浮动布局是CSS中一种非常强大的布局方式,最初设计用…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
