map和set介绍及其底层模拟实现
致努力前行的人:
要努力,但不要着急,繁花锦簇,硕果累累都需要过程!

目录
1.关联式容器
2.键值对
3.树形结构的关联式容器
3.1set的介绍
3.2set的使用
3.3multiset的使用
3.4map的使用
3.5multimap的使用
4.常见的面试题
5.底层结构
6.AVL树
6.1AVL树的概念
6.2AVL树节点的定义
6.3AVL树的插入
6.4AVL树的旋转
6.5AVL树的验证
6.6AVL树的性能
7.红黑树
7.1红黑树的概念
编辑 7.2红黑树的性质
7.3红黑树结点的定义
7.4红黑树的插入操作
7.5红黑树的验证
7.6实例代码:
7.8红黑树和AVL树的比较
8.红黑树模拟实现STL中的map和set
8.1STL中红黑树map和set结构搭建
8.2改造红黑树
8.3map的模拟实现
8.4set的模拟实现
1.关联式容器
在之前,我们已经接触过STL中的部分容器,比如:vector、list、deque等,这些容器统称为序列式容器,因为其底层为线性序列的数据结构,里面存储的是元素本身。那什么是关联式容器?它与序列式容器有什么区别?
关联式容器也是用来存储数据的,与序列式容器不同的是,其里面存储的是<key, value>结构的键值对,在数据检索时比序列式容器效率更高。
2.键值对
用来表示具有一一对应关系的一种结构,该结构中一般只包含两个成员变量key和value,key代表键值,value表示与key对应的信息。比如:现在要建立一个英汉互译的字典,那该字典中必然有英文单词与其对应的中文含义,而且,英文单词与其中文含义是一一对应的关系,即通过该应该单词,在词典中就可以找到与其对应的中文含义。
3.树形结构的关联式容器
根据应用场景的不同,STL总共实现了两种不同结构的管理式容器:树型结构与哈希结构。树型结构的关联式容器主要有四种:map、set、multimap、multiset。这四种容器的共同点是:使用平衡搜索树(即红黑树)作为其底层结果,容器中的元素是一个有序的序列。下面一依次介绍每一个容器。
3.1set的介绍
1. set是按照一定次序存储元素的容器
2. 在set中,元素的value也标识它(value就是key,类型为T),并且每个value必须是唯一的。set中的元素不能在容器中修改(元素总是const),但是可以从容器中插入或删除它们。
3. 在内部,set中的元素总是按照其内部比较对象(类型比较)所指示的特定严格弱排序准则进行排序。
4. set容器通过key访问单个元素的速度通常比unordered_set容器慢,但它们允许根据顺序对子集进行直接迭代。
5. set在底层是用二叉搜索树(红黑树)实现的。
注意:
1. 与set/multiset不同,map/multimap中存储的是真正的键值对<key, value>,set中只放value,但在底层实际存放的是由<value, value>构成的键值对。
2. set中插入元素时,只需要插入value即可,不需要构造键值对。
3. set中的元素不可以重复(因此可以使用set进行去重)。
4. 使用set的迭代器遍历set中的元素,可以得到有序序列
5. set中的元素默认按照小于来比较
6. set中查找某个元素,时间复杂度为:log n
7. set中的元素不允许修改.
8. set中的底层使用二叉搜索树(红黑树)来实现。
3.2set的使用
1.set的模板参数列表
 T: set中存放元素的类型,实际在底层存储<value, value>的键值对。
T: set中存放元素的类型,实际在底层存储<value, value>的键值对。
Compare:set中元素默认按照小于来比较
Alloc:set中元素空间的管理方式,使用STL提供的空间配置器管理
2.set的构造
| set (const Compare& comp = Compare(), const Allocator& = Allocator() ); | 构造空的set |
| set (InputIterator first, InputIterator last, const Compare& comp = Compare(), const Allocator& = Allocator() ); | 用[first, last)区间中的元素构造set |
| set ( const set<Key,Compare,Allocator>& x); | set的拷贝构造 |
void Test()
{set<int>s; //构造空的setvector<int>v;set<int>s1(v.begin(), v.end());//迭代器区间的元素构造setset<int>s2(s);//拷贝构造
}3. set的迭代器
| iterator begin() | 返回set中起始位置元素的迭代器 |
| iterator end() | 返回set中最后一个元素后面的迭代器 |
| const_iterator cbegin() const | 返回set中起始位置元素的const迭代器 |
| const_iterator cend() const | 返回set中最后一个元素后面的const迭代器 |
| reverse_iterator rbegin() | 返回set第一个元素的反向迭代器,即end |
| reverse_iterator rend() | 返回set最后一个元素下一个位置的反向迭代器,即rbegin |
| const_reverse_iterator crbegin() const | 返回set第一个元素的反向const迭代器,即cend |
| const_reverse_iterator crend() const | 返回set最后一个元素下一个位置的反向const迭代器,即crbegin |
使用set的迭代器遍历set中的元素,可以得到有序序列
void Test()
{set<int> s;s.insert(3);s.insert(10);s.insert(4);s.insert(9);s.insert(7);set<int>::iterator it = s.begin();while (it != s.end()){cout << *it << " ";it++;}cout << endl;
}
4.set的容量
| bool empty ( ) const | 检测set是否为空,空返回true,否则返回false |
| size_type size() const | 返回set中有效元素的个数 |

5.set修改操作
| pair<iterator,bool> insert (const value_type& x ) | 在set中插入元素x,实际插入的是<x, x>构成的 键值对,如果插入成功,返回<该元素在set中的 位置,true>,如果插入失败,说明x在set中已经 存在,返回<x在set中的位置,false> |
| void erase ( iterator position ) | 删除set中position位置上的元素 |
| size_type erase ( const key_type& x ) | 删除set中值为x的元素,返回删除的元素的个数 |
| void erase ( iterator first,iterator last ) | 删除set中[first, last)区间中的元素 |
| void swap (set<Key,Compare,Allocator>&st ); | 交换set中的元素 |
| void clear ( ) | 将set中的元素清空 |
| iterator find ( const key_type& x ) const | 返回set中值为x的元素的位置 |
| size_type count ( const key_type& x ) const | 返回set中值为x的元素的个数 |
void Test()
{set<int> s;//插入s.insert(3);s.insert(10);s.insert(4);s.insert(9);s.insert(7);//返回set中值为x的元素的位置set<int>::iterator ret = s.find(3);//删除set中position位置上的元素s.erase(ret);set<int>::iterator it = s.begin();while (it != s.end()){cout << *it << " ";it++;}cout << endl;cout << s.count(10) << endl; //返回set中值为10的元素的个数s.clear(); //将set中的元素清空
} 
3.3multiset的使用
1. multiset是按照特定顺序存储元素的容器,其中元素是可以重复的。
2. 在multiset中,元素的value也会识别它(因为multiset中本身存储的就是<value, value>组成的键值对,因此value本身就是key,key就是value,类型为T). multiset元素的值不能在容器中进行修改(因为元素总是const的),但可以从容器中插入或删除。
3. 在内部,multiset中的元素总是按照其内部比较规则(类型比较)所指示的特定严格弱排序准则进行排序。
4. multiset容器通过key访问单个元素的速度通常比unordered_multiset容器慢,但当使用迭代器遍历时会得到一个有序序列。
5. multiset底层结构为二叉搜索树(红黑树)。
注意:
1. multiset中再底层中存储的是<value, value>的键值对
2. mtltiset的插入接口中只需要插入即可
3. 与set的区别是,multiset中的元素可以重复,set是中value是唯一的
4. 使用迭代器对multiset中的元素进行遍历,可以得到有序的序列
5. multiset中的元素不能修改
6. 在multiset中找某个元素,时间复杂度为log n
7. multiset的作用:可以对元素进行排序
与set的区别是,multiset中的元素可以重复,set是中value是唯一的:
void Test()
{multiset<int> s;s.insert(3);s.insert(10);s.insert(10);s.insert(10);s.insert(10);s.insert(4);s.insert(9);s.insert(7);set<int>::iterator it = s.begin();while (it != s.end()){cout << *it << " ";it++;}cout << endl;cout << s.count(10) << endl;
} 

3.4map的使用
1. map是关联容器,它按照特定的次序(按照key来比较)存储由键值key和值value组合而成的元素。
2. 在map中,键值key通常用于排序和唯一地标识元素,而值value中存储与此键值key关联的内容。键值key和值value的类型可能不同,并且在map的内部,key与value通过成员类型value_type绑定在一起,为其取别名称为pair:
typedef pair<const key, T> value_type;
3. 在内部,map中的元素总是按照键值key进行比较排序的。
4. map中通过键值访问单个元素的速度通常比unordered_map容器慢,但map允许根据顺序对元素进行直接迭代(即对map中的元素进行迭代时,可以得到一个有序的序列)。
5. map支持下标访问符,即在[]中放入key,就可以找到与key对应的value。
6. map通常被实现为二叉搜索树(更准确的说:平衡二叉搜索树(红黑树))。
1.map的模板参数说明

key: 键值对中key的类型
T: 键值对中value的类型
Compare: 比较器的类型,map中的元素是按照key来比较的,缺省情况下按照小于来比较,一般情况下(内置类型元素)该参数不需要传递,如果无法比较时(自定义类型),需要用户自己显式传递比较规则(一般情况下按照函数指针或者仿函数来传递)
Alloc:通过空间配置器来申请底层空间,不需要用户传递,除非用户不想使用标准库提供的空间配置器
2.map的构造
map (const key_compare& comp = key_compare(),const allocator_type& alloc = allocator_type()); | 构造空的map |
template <class InputIterator>map (InputIterator first, InputIterator last,const key_compare& comp = key_compare(),const allocator_type& alloc = allocator_type()); | 用[first, last)区间中的元素构造map |
map (const map& x); | 拷贝构造 |
void Test()
{map<int, int>m; //构造空的mapvector<int>v;map<int, int>m1(v.begin(), v.end()); //用[first, last)区间中的元素构造mapmap<int, int>m2(m1); //拷贝构造
}3.map的迭代器
| begin()和end() | begin:首元素的位置,end最后一个元素的下一个位置 |
| cbegin()和cend() | 与begin和end意义相同,但cbegin和cend所指向的元素不能修改 |
| rbegin()和rend() | 反向迭代器,rbegin在end位置,rend在begin位置,其++和--操作与begin和end操作移动相反 |
| crbegin()和crend() | 与rbegin和rend位置相同,操作相同,但crbegin和crend所指向的元素不能修改 |
void Test()
{map<string, string>dict;dict.insert(pair<string, string>("排序", "sort"));dict.insert(pair<string, string>("左边", "left"));dict.insert(pair<string, string>("右边", "right"));//pair<string, string> 等价于 make_pairdict.insert(make_pair("字符串", "string"));map<string, string>::iterator it = dict.begin();while (it != dict.end()){//cout << (*it).first << ":" << (*it).second << endl;cout << it->first << ":" << it->second << endl;it++;}cout << endl;for (const auto& e : dict){cout << e.first << ":" << e.second << endl;}cout << endl;
} 4.map的容量与元素访问
4.map的容量与元素访问
| bool empty ( ) const | 检测map中的元素是否为空,是返回true,否则返回false |
| size_type size() const | 返回map中有效元素的个数 |
| mapped_type& operator[] (constkey_type& k) | 返回去key对应的value |


void Test()
{map<string, string>dict;dict.insert(pair<string, string>("排序", "sort"));dict.insert(pair<string, string>("左边", "left"));dict.insert(pair<string, string>("右边", "right"));dict["insert"]; //插入dict["insert"] = "插入"; //修改dict["iterator"] = "迭代器"; //插入+修改cout << dict["左边"] << endl; //key在就是查找
}5.map中元素的修改
| pair<iterator,bool> insert (const value_type& x ) | 在map中插入键值对x,注意x是一个键值 对,返回值也是键值对:iterator代表新插入 元素的位置,bool代表插入成功 |
| void erase ( iterator position ) | 删除position位置上的元素 |
| size_type erase ( const key_type& x ) | 删除键值为x的元素 |
| void erase ( iterator first, iterator last ) | 删除[first, last)区间中的元素 |
| void swap (map<Key,T,Compare,Allocator>&mp ) | 交换两个map中的元素 |
| void clear ( ) | 将map中的元素清空 |
| iterator find ( const key_type& x) | 在map中插入key为x的元素,找到返回该元 素的位置的迭代器,否则返回end |
| const_iterator find ( const key_type& x ) const | 在map中插入key为x的元素,找到返回该元 素的位置的const迭代器,否则返回cend |
| size_type count ( const key_type& x ) const | 返回key为x的键值在map中的个数,注意 map中key是唯一的,因此该函数的返回值 要么为0,要么为1,因此也可以用该函数来 检测一个key是否在map中 |
void Test()
{//统计水果出现的次数string arr[] = { "苹果", "西瓜", "香蕉", "草莓", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };map<string, int>countMap;for (const auto& e : arr){map<string, int>::iterator it = countMap.find(e);if (it == countMap.end()){countMap.insert(make_pair(e, 1));}else{it->second++;}}for (const auto& e : countMap){cout << e.first << ":" << e.second << endl;}cout << endl;
}
3.5multimap的使用
1. multimaps是关联式容器,它按照特定的顺序,存储由key和value映射成的键值对<key,value>,其中多个键值对之间的key是可以重复的。
2. 在multimap中,通常按照key排序和惟一地标识元素,而映射的value存储与key关联的内容。key和value的类型可能不同,通过multimap内部的成员类型value_type组合在一起,value_type是组合key和value的键值对:
typedef pair<const Key, T> value_type;
3. 在内部,multimap中的元素总是通过其内部比较对象,按照指定的特定严格弱排序标准对key进行排序的。
4. multimap通过key访问单个元素的速度通常比unordered_multimap容器慢,但是使用迭代器直接遍历multimap中的元素可以得到关于key有序的序列。
5. multimap在底层用二叉搜索树(红黑树)来实现
注意:multimap和map的唯一不同就是:map中的key是唯一的,而multimap中key是可以重复的。
multimap中的接口可以参考map,功能都是类似的。
void Test()
{multimap<string, string>dict;dict.insert(pair<string, string>("排序", "sort"));dict.insert(pair<string, string>("排序", "sort"));dict.insert(pair<string, string>("左边", "left"));dict.insert(pair<string, string>("左边", "left"));dict.insert(pair<string, string>("右边", "right"));dict.insert(pair<string, string>("右边", "right"));for (const auto& e : dict){cout << e.first << ":" << e.second << endl;}cout << endl;
}

4.常见的面试题
前K个高频单词
实现思路:定义一个map,然后将统计出现的字符串次数,然后放到一个vector<pair<int,string>>中,按照降序的方式进行排序,需要注意的是sort排序的时候是不稳定的,所以当出现的次数相同的时候,应该按照字典序的方式进行排序,然后将前k的字符串放到vector<string>中返回
class Solution {
public:struct Compare{bool operator()(const pair<int, string>& left, const pair<int, string>& right){return left.first > right.first || (left.first == right.first && left.second < right.second);}};vector<string> topKFrequent(vector<string>& words, int k) {map<string, int> countMap;for (const auto& e : words){countMap[e]++;}vector<pair<int, string>>v;for (const auto& e : countMap){v.push_back(make_pair(e.second, e.first));}sort(v.begin(), v.end(),Compare());vector<string>str;for (size_t i = 0; i < k; i++){str.push_back(v[i].second);}return str;}
};两个数组出现的交集
实现思路:实现set排序加去重的特性,如果两个数据相等就将数据加入到vector<int>中,否则就++数据小的那个迭代器
class Solution {
public:vector<int> intersection(vector<int>& nums1, vector<int>& nums2){set<int>s1(nums1.begin(), nums1.end());set<int>s2(nums2.begin(), nums2.end());vector<int>v;auto it1 = s1.begin();auto it2 = s2.begin();while (it1 != s1.end() && it2 != s2.end()){if (*it1 == *it2){v.push_back(*it1);it1++;it2++;}else if (*it1 > *it2)++it2;else++it1;}return v;}
};
5.底层结构
前面对map/multimap/set/multiset进行了简单的介绍,这几个容器有个共同点是:其底层都是按照二叉搜索树来实现的,但是二叉搜索树有其自身的缺陷,假如往树中插入的元素有序或者接近有序,二叉搜索树就会退化成单支树,时间复杂度会退化成O(N),因此
map、set等关联式容器的底层结构是对二叉树进行了平衡处理,即采用平衡树来实现。
6.AVL树
6.1AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:

它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在logn,搜索时间复杂度O(log n)。
一般规定:平衡因子 = 右子树的高度 - 左子树的高度
6.2AVL树节点的定义
template<class K,class V>
struct AVLTreeNode
{pair<K, V>_kv;AVLTreeNode<K, V>* _left; // 该节点的左孩子AVLTreeNode<K, V>* _right; //该节点的右孩子AVLTreeNode<K, V>* _parent; // 该节点的双亲int _bf; //balance fectorAVLTreeNode(const pair<K, V> kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0) {}
};6.3AVL树的插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步:
1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子
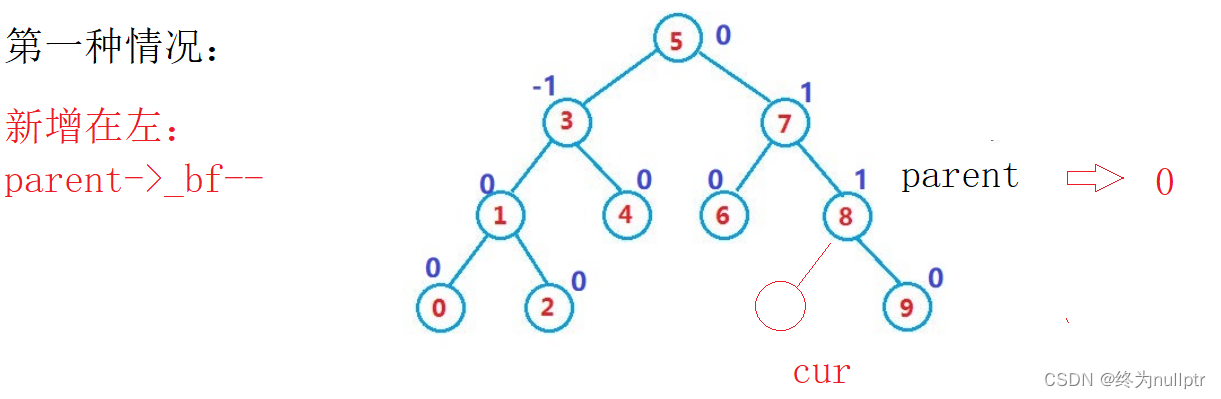

 更新完之后是否继续更新判断标准:
更新完之后是否继续更新判断标准:
1.parent->_bf == 0,说明之前parent->_bf是1或者是-1,也就是说parent一边高一边低,这次插入填上矮的那边,parent所在子树高度不变,不需要继续往上更新
2、parent->_bf == 1 或 -1 说明之前是parent->_bf == 0,两边一样高,现在插入一边更高了,parent所在子树高度变了,继续往上更新
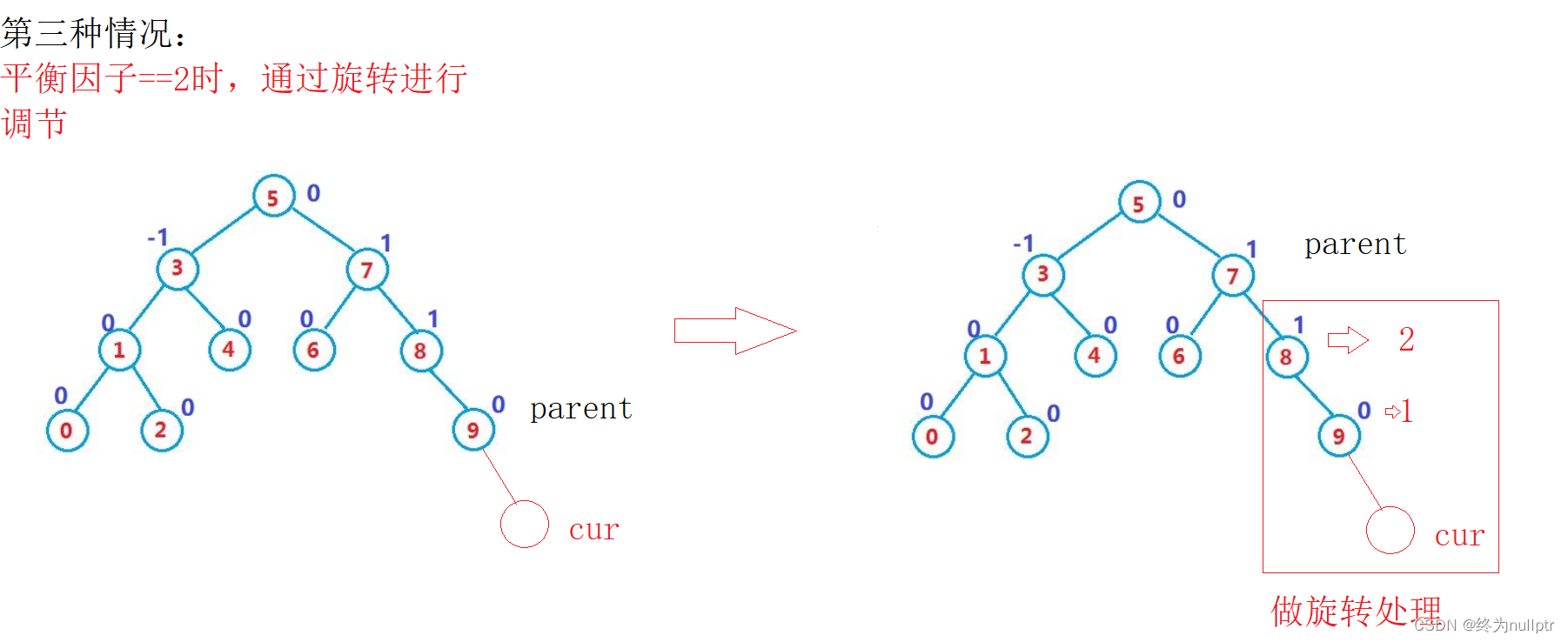
3、parent->_bf == 2 或 -2,说明之前parent->_bf == 1 或者 -1,现在插入严重不平衡,违反规则,需要做旋转处理
旋转后需要达成的目标:
1.让这颗子树的左右高度不超过1;
2.旋转完之后继续保持是二叉搜索树
3.更新调整孩子结点的平衡因子
4.让这颗子树的高度跟插入前保持一致
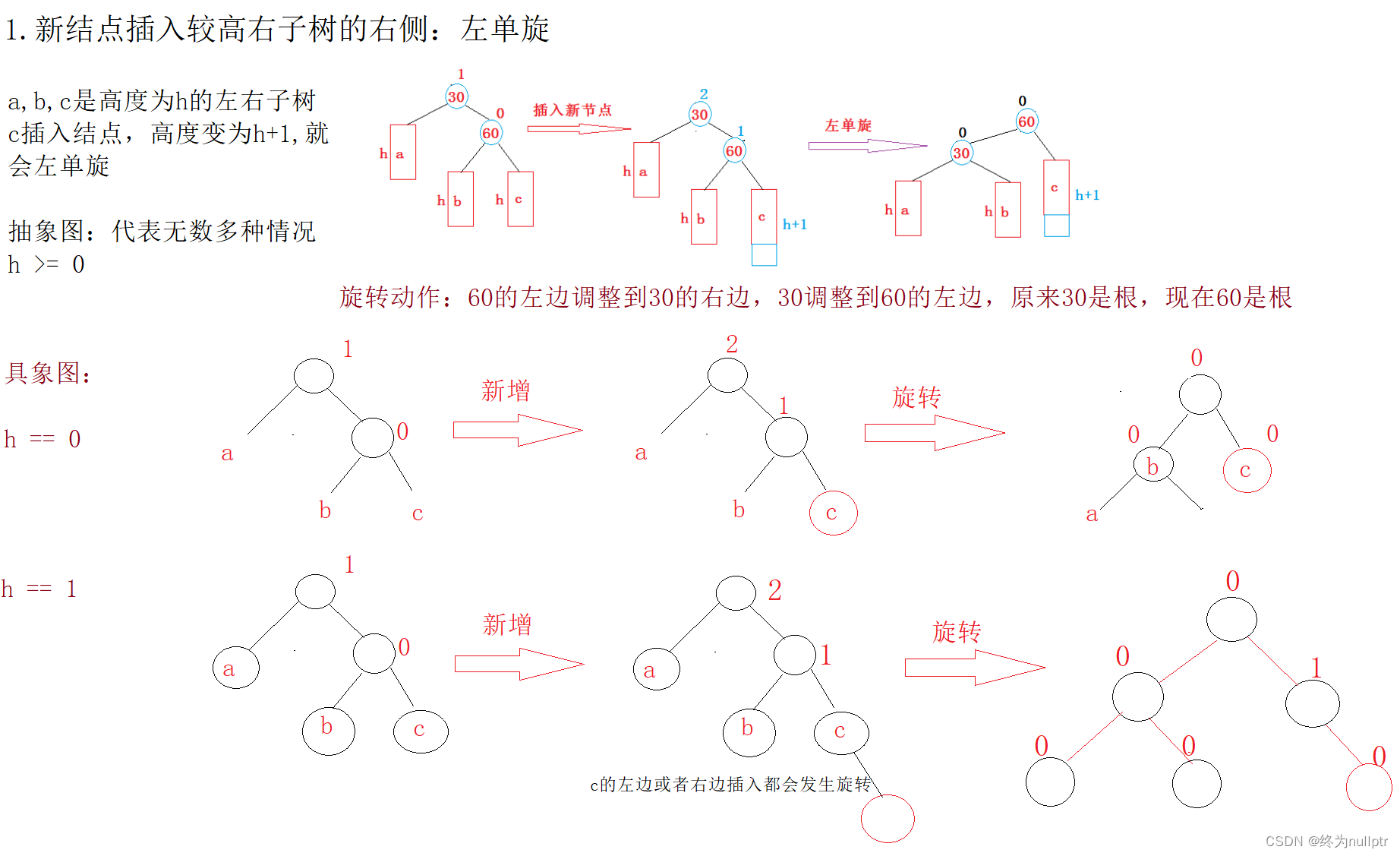
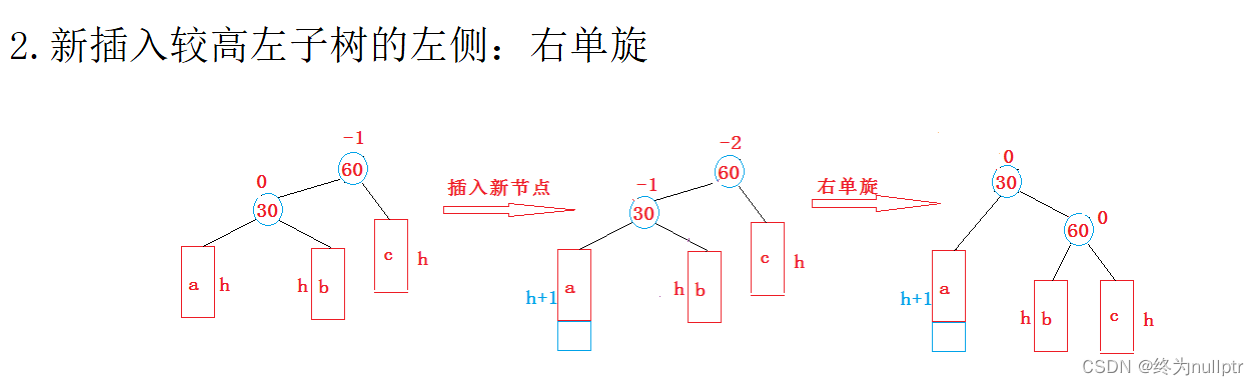
6.4AVL树的旋转
AVL树的旋转分为四种:

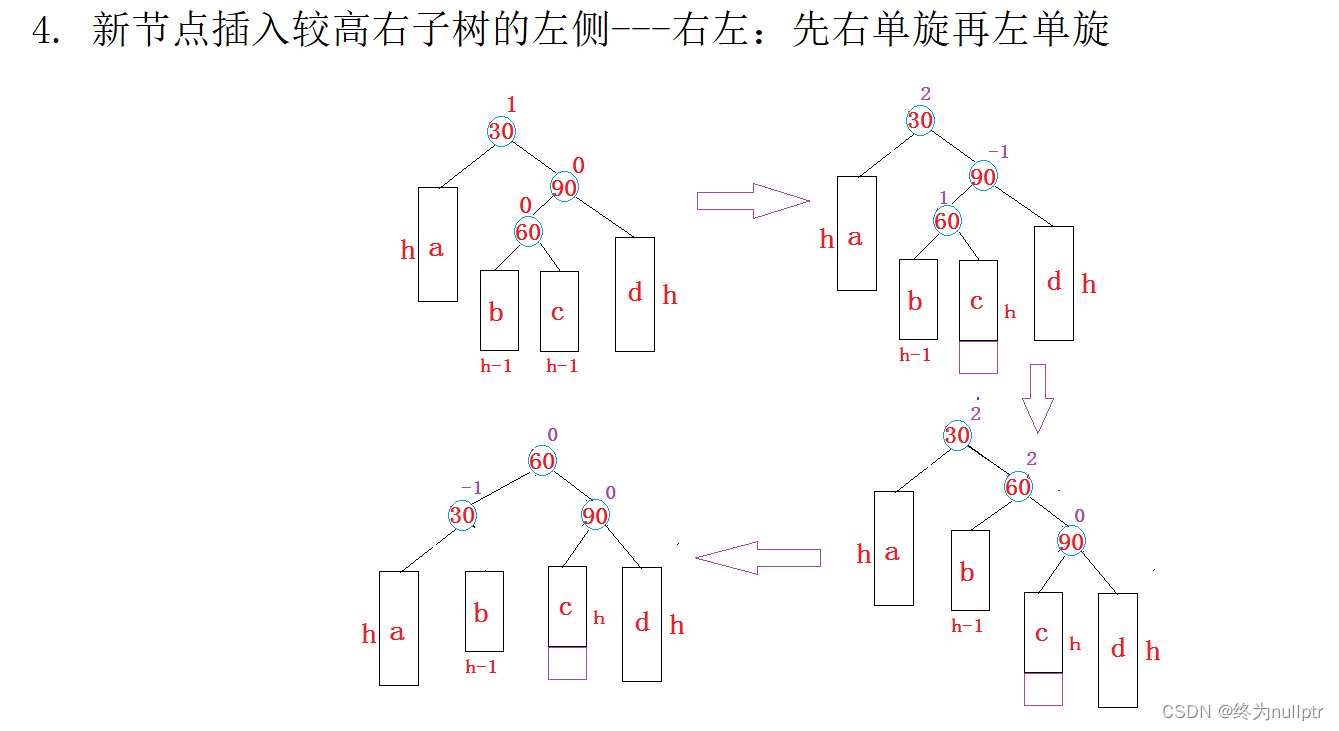
6.5AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
1. 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
2. 验证其为平衡树
每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
节点的平衡因子是否计算正确
6.6AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即log2 N。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数
据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
实例代码:
template<class K, class V> class AVLTree {typedef AVLTreeNode<K, V> Node; public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}else{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//调整平衡因子:while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}}return true;}void Inorder(){_Inorder(_root);}bool IsBalance(){return _IsBalance(_root);} private:bool _IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (rightHeight - leftHeight != root->_bf){return false;}return abs(rightHeight - leftHeight) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);}int Height(Node* root){if (root == nullptr)return 0;int lh = Height(root->_left);int rh = Height(root->_right);return lh > rh ? lh + 1 : rh + 1;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}parent->_bf = subR->_bf = 0;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode == nullptr){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}parent->_bf = subL->_bf = 0;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);//subLR的左子树新增if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}//subLR的右子树新增else if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}//subLR自己本身就是新增else if(bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else{assert(false);}}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);//subRL的右子树新增if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}//subLR的左子树新增else if (bf == -1){subRL->_bf = 0;subR->_bf = 1;parent->_bf = 0;}//subRL自己本身就是新增else if (bf == 0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else{assert(false);}} private:void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}private:Node* _root = nullptr; };
7.红黑树
7.1红黑树的概念
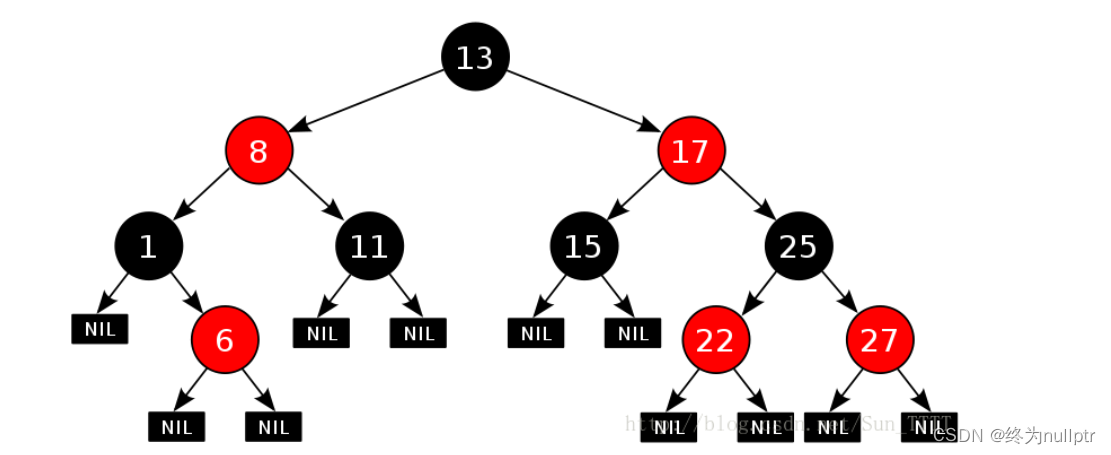
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
如图所示
 7.2红黑树的性质
7.2红黑树的性质
1.每个结点不是红色就是黑色
2.根节点是黑色的
3.如果一个结点是红色的,则它的两个孩子结点是黑色的(没有连续的红色结点)
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点 (每条路径上都包含相同数量的黑色结点)
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍
7.3红黑树结点的定义
//结点的颜色
enum Color
{RED,BLACK
};
template<class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _col;RBTreeNode(const pair<K, V> kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED) {}
};7.4红黑树的插入操作
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
1. 按照二叉搜索的树规则插入新节点
2. 检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
情况一: cur为红,p为红,g为黑,u存在且为红
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
如图所示:

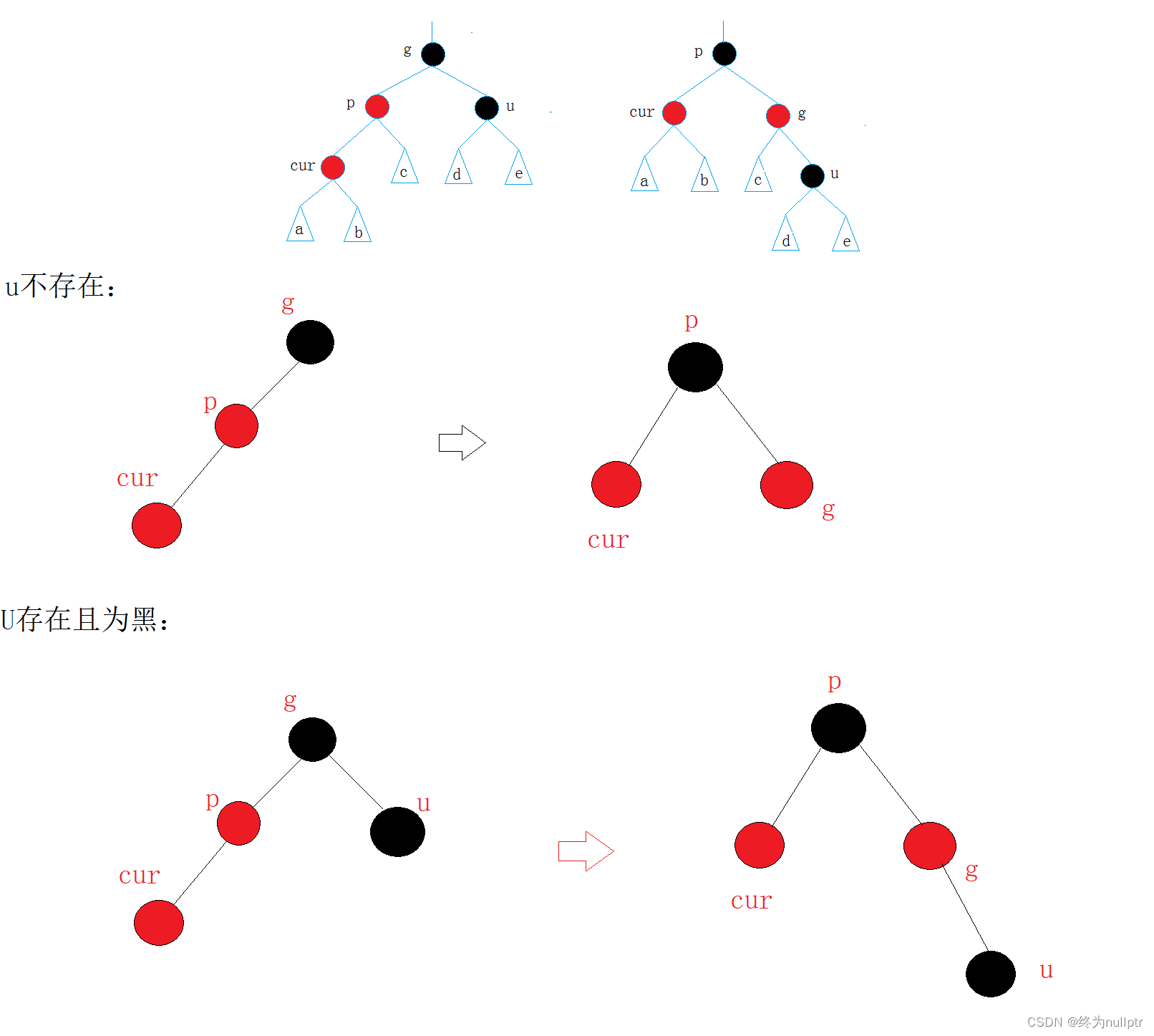
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
解决方式:p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色--p变黑,g变红
如图所示
情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑
解决方式:p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,p为g的右孩子,cur为p的左孩子,则针对p做右单旋转则转换成了情况2(双旋转)
如图所示:

7.5红黑树的验证
红黑树的检测分为两步:
1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
2. 检测其是否满足红黑树的性质
7.6实例代码:
//结点的颜色
enum Color
{RED,BLACK
};
template<class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _col;RBTreeNode(const pair<K, V> kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED) {}
};template<class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (grandfather == nullptr)break;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else{if (cur == parent->_left){//情况二:RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//情况三:RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;parent = grandfather->_parent;cur = grandfather;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void Inorder(){_Inorder(_root);}bool IsBalance(){if (_root == nullptr)return false;//判断根节点:if (_root->_col != BLACK)return false;//获取任意路径上黑色节点的数量:int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK)ref++;left = left->_left;}return CheckRBTree(_root, 0, ref);}
private:bool CheckRBTree(Node* root, int blackNum, int ref){if (root == nullptr){if (blackNum != ref){cout << "违反规则:本条路径上黑色结点的数量和最左路径上的不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则:出现连续的红色结点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return CheckRBTree(root->_left, blackNum, ref) &&CheckRBTree(root->_right, blackNum, ref);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode == nullptr){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}
private:Node* _root = nullptr;
};7.8红黑树和AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是Olog2 N,红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
8.红黑树模拟实现STL中的map和set
8.1STL中红黑树map和set结构搭建

8.2改造红黑树
enum Color
{RED,BLACK
};
template<class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Color _col;RBTreeNode(const T& val):_data(val), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED) {}
};
template<class T,class Ref,class Ptr>
struct __RBTreeIterator
{typedef RBTreeNode<T> Node;typedef __RBTreeIterator<T,Ref,Ptr> Self;typedef __RBTreeIterator<T, T&, T*> iterator;Node* _node;__RBTreeIterator(Node* node):_node(node) {}//普通迭代器的时候,是拷贝构造//const迭代器的时候,是构造,用普通迭代器构造const迭代器__RBTreeIterator(const iterator& s):_node(s._node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}Self& operator++(){if (_node->_right){Node* min = _node->_right;while (min->_left){min = min->_left;}_node = min;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}Self& operator--(){if (_node->_left){Node* max = _node->_left;while (max->_right){max = max->_right;}_node = max;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}bool operator != (const Self& s) {return _node != s._node;}bool operator==(const Self& s){return _node == s._node;}
};
template<class K,class T,class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef __RBTreeIterator<T,T&,T*> iterator;typedef __RBTreeIterator<T, const T&, const T*> const_iterator;iterator begin(){Node* left = _root;while (left->_left){left = left->_left;}return iterator(left);}iterator end(){return iterator(nullptr);}iterator begin() const{Node* left = _root;while (left->_left){left = left->_left;}return iterator(left);}iterator end() const{return iterator(nullptr);}pair<iterator,bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);return make_pair(iterator(_root), true);}KeyOfT kot;Node* cur = _root;Node* parent = nullptr;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(iterator(cur), false);}}cur = new Node(data);Node* newNode = cur;if (kot(parent->_data) < kot(data)){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (grandfather == nullptr)break;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else{if (cur == parent->_left){//情况二:RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//情况三:RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;parent = grandfather->_parent;cur = grandfather;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(iterator(newNode), true);}void Inorder(){_Inorder(_root);}bool IsBalance(){if (_root == nullptr)return false;//判断根节点:if (_root->_col != BLACK)return false;//获取任意路径上黑色节点的数量:int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK)ref++;left = left->_left;}return CheckRBTree(_root, 0, ref);}
private:bool CheckRBTree(Node* root, int blackNum, int ref){if (root == nullptr){if (blackNum != ref){cout << "违反规则:本条路径上黑色结点的数量和最左路径上的不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则:出现连续的红色结点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return CheckRBTree(root->_left, blackNum, ref) &&CheckRBTree(root->_right, blackNum, ref);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode == nullptr){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}
private:Node* _root = nullptr;
};8.3map的模拟实现
namespace ns
{template<class K, class V>class map{struct MapKeyOfT{const K& operator()(const pair<const K, V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end() const{return _t.end();}pair<iterator, bool> insert(const pair<K, V>& kv){return _t.Insert(kv);}V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;};8.4set的模拟实现
namespace ns
{template<class K>class set{struct SetKeyOfT{const K& operator()(const K& key){return key;}};public:typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}pair<iterator,bool> insert(const K& key){pair<typename RBTree<K, K, SetKeyOfT>::iterator, bool> ret = _t.Insert(key);return pair<iterator, bool>(ret.first, ret.second);}private:RBTree<K, K, SetKeyOfT> _t;};相关文章:

map和set介绍及其底层模拟实现
致努力前行的人: 要努力,但不要着急,繁花锦簇,硕果累累都需要过程! 目录 1.关联式容器 2.键值对 3.树形结构的关联式容器 3.1set的介绍 3.2set的使用 3.3multiset的使用 3.4map的使用 3.5multimap的使用 4.常见的面试题…...

实现一个比ant功能更丰富的Modal组件
普通的modal组件如下: 我们写的modal额外支持,后面没有蒙版,并且Modal框能够拖拽 还支持渲染在文档流里,上面的都是fixed布局,我们这个正常渲染到文档下面: render部分 <RenderDialog{...restState}visi…...

2023美赛F题思路数据代码分享
文章目录赛题思路2023年美国大学生数学建模竞赛选题&论文一、关于选题二、关于论文格式三、关于论文提交四、论文提交流程注意不要手滑美赛F题思路数据代码【最新】赛题思路 (赛题出来以后第一时间在CSDN分享) 最新进度在文章最下方卡片,加入获取一手资源 202…...
进行交互)
Flutter如何与Native(Android)进行交互
前言 上一篇文章《Flutter混合开发:Android中如何启动Flutter》中我们介绍了如何在Native(Android项目)中启动Flutter,展示Flutter页面。但是在开发过程中,很多时候并不是简单的展示一个页面即可,还会涉及…...

数据库主从复制和读写分离
主从数据库和数据库集群的一些问题 数据库集群和主从数据库最本质的区别,其实也就是data-sharing和nothing-sharing的区别。集群是共享存储的。主从复制中没有任何共享。每台机器都是独立且完整的系统。 什么是主从复制? 主从复制,是用来建立一个和主数…...
Java并发编程面试题——线程安全(原子性、可见性、有序性)
文章目录一、原子性高频问题1.1 Java中如何实现线程安全?1.2 CAS底层实现1.3 CAS的常见问题1.4 四种引用类型 ThreadLocal的问题?二、可见性高频问题2.1 Java的内存模型2.2 保证可见性的方式2.3 volatile修饰引用数据类型2.4 有了MESI协议,为啥还有vol…...

DialogFragment内存泄露问题能不能一次性改好
孽缘 自DialogFragment在Android3.0之后作为一种特殊的Fragment引入,官方建议使用DialogFragment代替Dialog或者AllertDialog来实现弹框的功能,因为它可以更好的管理Dialog的生命周期以及可以更好复用。 然而建议虽好,实用须谨慎,…...
java学习--多线程
多线程 了解多线程 多线程是指从软件或者硬件上实现多个线程并发执行的技术。 具有多线程能力的计算机因有硬件支持而能够在同一时间执行多个线程,提升性能。 并发和并行 并行:在同一时刻,有多个指令在CPU上同时执行并发࿱…...

90后阿里P7技术专家晒出工资单:狠补了这个,真香...
最近一哥们跟我聊天装逼,说他最近从阿里跳槽了,我问他跳出来拿了多少?哥们表示很得意,说跳槽到新公司一个月后发了工资,月入5万多,表示很满足!这样的高薪资着实让人羡慕,我猜这是税后…...
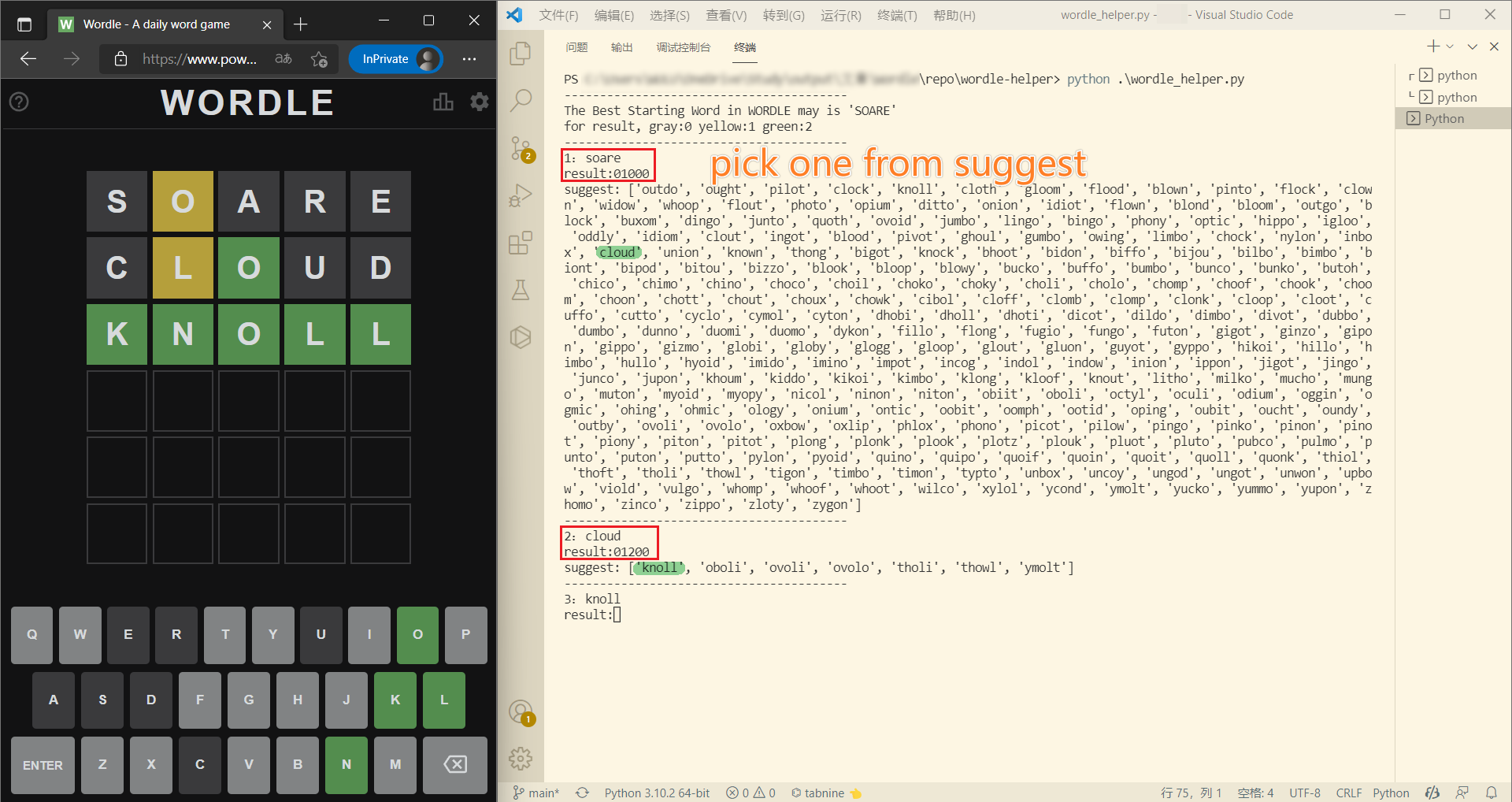
2023美赛C题:Wordle筛选算法
Wordle 规则介绍 Wordle 每天会更新一个5个字母的单词,在6次尝试中猜出单词就算成功。每个猜测必须是一个有效的单词(不能是不能组成单词的字母排列)。 每次猜测后,字母块的颜色会改变,颜色含义如下: 程…...
SpringBoot 集成 Kafka
SpringBoot 集成 Kafka1 安装 Kafka2 创建 Topic3 Java 创建 Topic4 SpringBoot 项目4.1 pom.xml4.2 application.yml4.3 KafkaApplication.java4.4 CustomizePartitioner.java4.5 KafkaInitialConfig.java4.6 SendMessageController.java5 测试1 安装 Kafka Docker 安装 Kafk…...

OpenCV 图像金字塔算子
本文是OpenCV图像视觉入门之路的第14篇文章,本文详细的介绍了图像金字塔算子的各种操作,例如:高斯金字塔算子 、拉普拉斯金字塔算子等操作。 高斯金字塔中的较高级别(低分辨率)是通过先用高斯核对图像进行卷积再删除偶…...

【自学Linux】Linux一切皆文件
Linux一切皆文件 Linux一切皆文件教程 Linux 中所有内容都是以文件的形式保存和管理的,即一切皆文件,普通文件是文件,目录是文件,硬件设备(键盘、监视器、硬盘、打印机)是文件,就连套接字&…...

CUDA C++扩展的详细描述
CUDA C扩展的详细描述 文章目录CUDA C扩展的详细描述CUDA函数执行空间说明符B.1.1 \_\_global\_\_B.1.2 \_\_device\_\_B.1.3 \_\_host\_\_B.1.4 Undefined behaviorB.1.5 __noinline__ and __forceinline__B.2 Variable Memory Space SpecifiersB.2.1 \_\_device\_\_B.2.2. \_…...

为什么重写equals必须重写hashCode
关于这个问题,看了网上很多答案,感觉都参差不齐,没有答到要点,这次就记录一下! 首先我们为什么要重写equals?这个方法是用来干嘛的? public boolean equals (Object object&#x…...

< 每日小技巧:N个很棒的 Vue 开发技巧, 持续记录ing >
每日小技巧:6 个很棒的 Vue 开发技巧👉 ① Watch 妙用> watch的高级使用> 一个监听器触发多个方法> watch 监听多个变量👉 ② 自定义事件 $emit() 和 事件参数 $event👉 ③ 监听组件生命周期常规写法hook写法ὄ…...

数据结构与算法之二分查找分而治之思想
决定我们成为什么样人的,不是我们的能力,而是我们的选择。——《哈利波特与密室》二分查找是查找算法里面是很优秀的一个算法,特别是在有序的数组中,这种算法思想体现的淋漓尽致。一.题目描述及其要求请实现无重复数字的升序数组的…...
训练自己的中文word2vec(词向量)--skip-gram方法
训练自己的中文word2vec(词向量)–skip-gram方法 什么是词向量 将单词映射/嵌入(Embedding)到一个新的空间,形成词向量,以此来表示词的语义信息,在这个新的空间中,语义相同的单…...

ubuntu系统环境配置和常用软件安装
系统环境 修改文件夹名称为英文 参考链接 export LANGen_US xdg-user-dirs-gtk-update 常用软件安装 常用工具 ping 和ifconfig工具 sudo apt install -y net-tools inetutils-ping 截图软件 sudo apt install -y net-tools inetutils-ping flameshot 录屏 sudo apt-get i…...
【1139. 最大的以 1 为边界的正方形】
来源:力扣(LeetCode) 描述: 给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。 示例 1&#…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
