ChatGPT在高等教育中的应用利弊探讨

人工智能在教育领域的应用日益广泛。2022年11月OpenAI开发的聊天机器人ChatGPT在全球范围内流传开来,其中用户数量最多的国家是美国(15.22%)。由于ChatGPT应用广泛,具有类似人类回答问题的能力,它正在成为许多学生和教育工作者的可信赖伙伴。然而,与任何新兴技术一样,ChatGPT在高等教育中的应用也面临一定的挑战。[1]
ChatGPT应用在高等教育中的利处
提高教育普及性
ChatGPT为一些残疾人士和非英语用户消除了学习障碍。例如,ChatGPT可以为视力受损的学生语音播报回答内容。它还可以为有学习障碍学生总结课程中的主题或概念。同时,ChatGPT还能使那些不能使用键盘输入的学生用语音输入的方式完成会话。
ChatGPT可以结合语境更加智能地将英文内容翻译成学生熟悉的语言,让他们更加轻松地理解课程内容。
辅助完成作业
通常,学生需要翻阅课本和互联网来寻找相关的作业材料。与此不同,ChatGPT可以节省时间并使作业完成得更容易。
当学生向ChatGPT提问时,它会以解释和示例的方式回答。ChatGPT为学生提供了一种解题的新思路。同时,它还会提供与特定背景相关的学术短语、术语和语句结构,从而丰富学生的专项词汇和写作能力。
为教育工作者提供帮助
在高等教育中,ChatGPT可以以多种方式帮助到教育工作者,如下所示:
为一个课程开发全面的教学计划。
生成各种测验题型,如选择题、判断题、填空题等。
分析学生的作业,并帮助教师评分和提供建设性意见。
提供课程之外的相关教学资源链接。
提供如何提高学生课堂参与度的技巧和减少学生课堂不良行为的诀窍。
个性化学习
ChatGPT可以了解学生的学习方式,提供个性化的学习体验。它可以分析学生的表现,并调整课程学习内容以满足他们的实际要求。
通过ChatGPT,学生可以以舒适的节奏学习,彻底理解复杂的概念。他们可以通过与ChatGPT进行独特的学习相关对话,快速获取课堂以外的额外学习成果。
此外,在ChatGPT的个性化反馈帮助下,他们也可以提高学术论文的质量。
帮助准备考试
当考试临近时,ChatGPT可以复述并强调他们课堂笔记中的关键要点。此外,它还可以生成练习题,让学生了解自己哪些方面掌握得好,哪些方面还需努力。
高等教育中应用ChatGPT的弊端
缺乏学术诚信
学术诚信是ChatGPT应用在高等教育中的首要问题。许多教育工作者认为,使用ChatGPT写作业只会促进作弊和剽窃。由于ChatGPT可以快速生成答案,这会降低学生的头脑风暴、批判性思维和创造性回答的能力。
提供不准确的信息
ChatGPT提供的信息可能看起来合理,但不一定准确。很难准确检测它哪部分的信息,真的是错的。这可能会影响学生的学习体验及成果。
有偏见的回复
AI聊天机器人是通过海量数据集进行训练的。如果数据集包含偏见,ChatGPT产生的一些回复就有可能存在偏见。这些偏见是有害的,可能会放大对某种歧视,并助长不良风气。
知识有限
尽管ChatGPT经过大量信息训练,但仍有一些信息无法访问。因此,它可能无法就小众主题提供好的答案。它也可能不了解不同领域的最新进展。
无法开展多任务和真正理解上下文
ChatGPT一次只能处理一项任务并回复一个查询。如果学生一次问多个问题,ChatGPT可能会难以确定回答的优先顺序并在回答所有问题之前放慢速度。
此外,ChatGPT有时会难以理解上下文。例如,如果学生在问题中使用了幽默或讽刺,ChatGPT可能无法捕捉到这一点并提供不相关的回复。
缺乏情商
情商在教育环境中发挥着重要作用。人类教育者可以理解学生的情绪并相应地做出回应。教育工作者一般都会在教学的过程中提供情感支持。但这在缺乏情商的ChatGPT等虚拟聊天机器上可不是这样的。尽管它们的回复会表现得很有同情心,但实际上它们无法对复杂的人类情感做出适当的回应。
结语
一方面,ChatGPT具有许多优点,包括创建个性化互动课程、提高受教育机会、帮助教育工作者策划课程等。另一方面,ChatGPT也存在许多缺点,包括可能产生有偏见的回复、提供不准确信息、无法多任务处理工作等。
尽管存在利弊,ChatGPT仍在不断发展,预计到2024年,其收入将增长到10亿美元。[2]
参考资料
[1]https://www.94c.cc/info/pros-and-cons-of-chatgpt-in-higher-education.html
[2]https://www.hurix.com/chat-gpt-pros-and-cons-of-using-chatgpt-in-higher-education/
相关文章:

ChatGPT在高等教育中的应用利弊探讨
人工智能在教育领域的应用日益广泛。2022年11月OpenAI开发的聊天机器人ChatGPT在全球范围内流传开来,其中用户数量最多的国家是美国(15.22%)。由于ChatGPT应用广泛,具有类似人类回答问题的能力,它正在成为许多学生和教育工作者的可信赖伙伴…...

Java之API详解之Runtime的详细解析
3.1 概述 Runtime表示Java中运行时对象,可以获取到程序运行时设计到的一些信息 3.2 常见方法 常见方法介绍 我们要学习的Object类中的常见方法如下所示: public static Runtime getRuntime() //当前系统的运行环境对象 public void exit(int statu…...

机器学习之softmax
Softmax是一个常用于多类别分类问题的激活函数和归一化方法。它将一个向量的原始分数(也称为 logits)转换为概率分布,使得每个类别的概率值在0到1之间,同时确保所有类别的概率之和等于1。Softmax函数的定义如下: 对于…...

npm script命令
1 串行/并行执行命令 //串行 npm-run-all text test npm run text && npm run test //并行改成& npm-run-all --parallel text test npm run text & npm run test2 传递参数 {"lint": "eslint js/*.js","lint:fix":…...

【力扣周赛】第360场周赛
【力扣周赛】第360场周赛 8015.距离原点最远的点题目描述解题思路 8022. 找出美丽数组的最小和题目描述解题思路 8015.距离原点最远的点 题目描述 描述:给你一个长度为 n 的字符串 moves ,该字符串仅由字符 ‘L’、‘R’ 和 ‘_’ 组成。字符串表示你在…...

php环境变量的配置步骤
要配置PHP的环境变量,以便在命令行中直接使用php命令,以下是一般的步骤: Windows 操作系统 下载和安装PHP:首先,你需要从PHP官方网站(https://www.php.net/downloads.php)下载适用于你的操作系…...

Kdtree
Kdtree kdtree 就是在 n 维空间对数据点进行二分;具体先确定一个根,然后小于在这个维度上的根的节点在左边,大于的在右边,再进行下一个维度的划分。直到维度结束,再重复,或者直到达到了结束条件࿱…...
算法leetcode|74. 搜索二维矩阵(rust重拳出击)
文章目录 74. 搜索二维矩阵:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 74. 搜索二维矩阵: 给你一个满足下述两条属性的…...

element浅尝辄止7:InfiniteScroll 无限滚动
滚动加载:滚动至底部时,加载更多数据。 1.如何使用? //在要实现滚动加载的列表上上添加v-infinite-scroll,并赋值相应的加载方法, //可实现滚动到底部时自动执行加载方法。<template><ul class"infinit…...

Day05-Vue基础
Day05-Vue基础 一、单向数据流 父子组件通信。会在父组件中定义好数据,将数据传递给子组件,可以使用这个数据 Vue中针对props这个属性提出了一个单向数据流的概念。 Vue针对props做了一些限制,可以接受值,使用这个值,规范中不要去直接修改这个值 目的是为了对数据流进…...
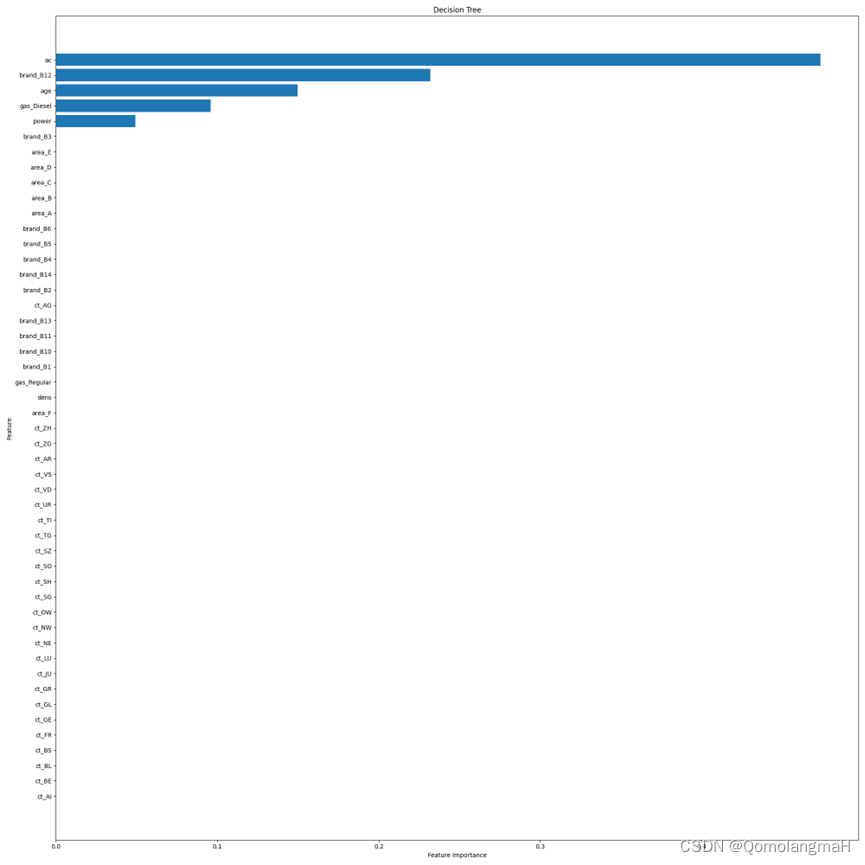
《机器学习在车险定价中的应用》实验报告
目录 一、实验题目 机器学习在车险定价中的应用 二、实验设置 1. 操作系统: 2. IDE: 3. python: 4. 库: 三、实验内容 实验前的猜想: 四、实验结果 1. 数据预处理及数据划分 独热编码处理结果(以…...
14. Docker中实现CI和CD
目录 1、前言 2、什么是CI/CD 3、部署Jenkins 3.1、下载Jenkins 3.2、启动Jenkins 3.3、访问Jenkins页面 4、Jenkins部署一个应用 5、Jenkins实现Docker应用的持续集成和部署 5.1、创建Dockerfile 5.2、集成Jenkins和Docker 6、小结 1、前言 持续集成(CI/CD)是一种…...

【多思路解决喝汽水问题】1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水
题目内容 喝汽水问题 喝汽水,1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水(编程实现)。 题目分析 数学思路分析 根据给出的问题和引用内容,我们可以得出答案。 首先ÿ…...
)
P1591 阶乘数码(Java高精度)
题目描述 求 n ! n! n! 中某个数码出现的次数。 输入格式 第一行为 t ( t ≤ 10 ) t(t \leq 10) t(t≤10),表示数据组数。接下来 t t t 行,每行一个正整数 n ( n ≤ 1000 ) n(n \leq 1000) n(n≤1000) 和数码 a a a。 输出格式 对于每组数据&a…...

Mybatis的动态SQL及关键属性和标识的区别(对SQL更灵活的使用)
( 虽然文章中有大多文本内容,想了解更深需要耐心看完,必定大有受益 ) 目录 一、动态SQL ( 1 ) 是什么 ( 2 ) 作用 ( 3 ) 优点 ( 4 ) 特殊标签 ( 5 ) 演示 二、#和$的区别 2.1 #使用 ( 1 ) #占位符语法 ( 2 ) #优点 2.…...
mysql下载
网址 MySQL :: Download MySQL Community Serverhttps://dev.mysql.com/downloads/mysql/ 2、选择MSI进行安装 3、这里我选择离线安装 4、这里我选择直接下载 5、等待下载安装即可...

聚合函数与窗口函数
聚合函数 回答一 聚合函数(Aggregate Functions)是SQL中的函数,用于对一组数据进行计算,并返回单个结果。聚合函数通常用于统计和汇总数据,包括计算总和、平均值、计数、最大值和最小值等。 以下是一些常见的聚合函…...
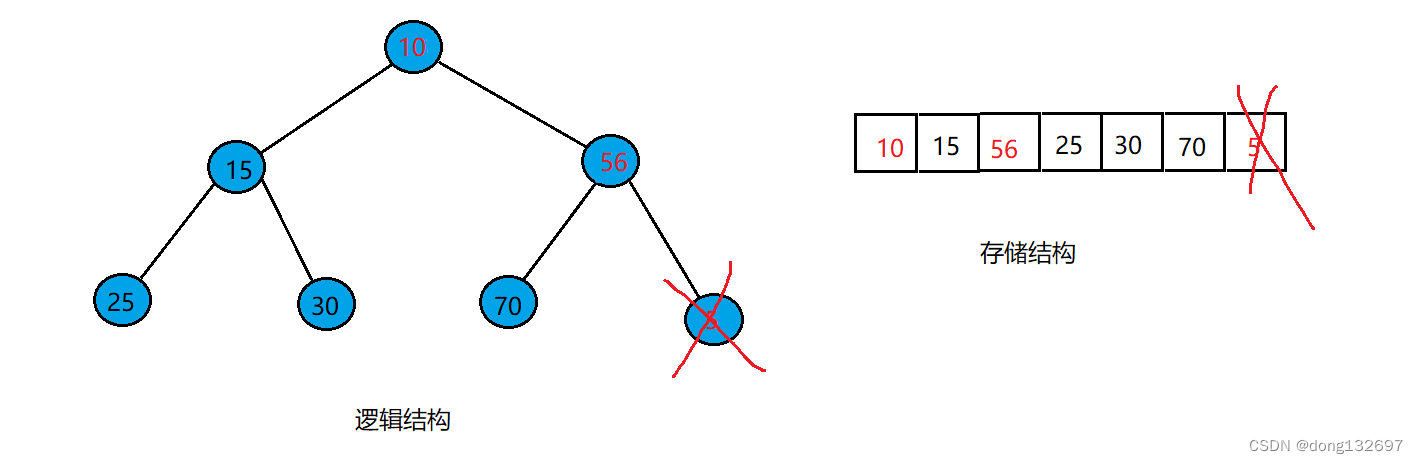
c语言实现堆
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、树1、树的概念2、树的相关概念3、树的表示 二、二叉树1、二叉树概念2、特殊的二叉树3、二叉树的性质4、二叉树的顺序结构5、二叉树的链式结构 三、堆(二叉树…...

ubuntu 如何将文件打包成tar.gz
要将文件打包成.tar.gz文件,可以使用以下命令: tar -czvf 文件名.tar.gz 文件路径 其中,-c表示创建新的归档文件,-z表示使用gzip进行压缩,-v表示显示详细的打包过程,-f表示指定归档文件的名称。 例如&am…...
)
前端优化页面加载速度的方法(持续更新)
提速方法方向 延迟脚本加载 使用 async 属性: 在这种方法中,脚本将在下载完成后立即执行,而不会阻塞其他页面资源的加载和渲染。这适用于那些不依赖于其他脚本和页面内容的脚本,例如分析脚本等。示例如下: html …...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
