排序算法概述
1.排序算法分类
-
**比较类算法排序:**通过比较来决定元素的时间复杂度的相对次序,由于其时间复杂度不能突破 O ( n l o g n ) O(nlogn) O(nlogn),因此也称为非线性时间比较类算法
-
**非比较类算法排序:**不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行。
排序算法
2.排序算法性能指标
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 插入排序 | O ( n 2 ) O({n^2}) O(n2) | O ( n 2 ) O({n^2}) O(n2) | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) | 稳定 |
| 希尔排序 | O ( n 2 / 3 ) O(n^{2/3}) O(n2/3) | O ( n 2 ) O({n^2}) O(n2) | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) | 不稳定 |
| 选择排序 | O ( n 2 ) O({n^2}) O(n2) | O ( n 2 ) O({n^2}) O(n2) | O ( n 2 ) O({n^2}) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 堆排序 | O ( n l o g 2 n ) O(n{log_2}n) O(nlog2n) | O ( n l o g 2 n ) O(n{log_2}n) O(nlog2n) | O ( n l o g 2 n ) O(n{log_2}n) O(nlog2n) | O ( 1 ) O(1) O(1) | 不稳定 |
| 冒泡排序 | O ( n 2 ) O({n^2}) O(n2) | O ( n 2 ) O({n^2}) O(n2) | O ( n ) O({n}) O(n) | O ( 1 ) O(1) O(1) | 稳定 |
| 快速排序 | O ( n l o g 2 n ) O(n{log_2}n) O(nlog2n) | O ( n 2 ) O({n^2}) O(n2) | O ( n l o g 2 n ) O(n{log_2}n) O(nlog2n) | O ( n l o g 2 n ) O(n{log_2}n) O(nlog2n) | 不稳定 |
| 归并排序 | O ( n l o g 2 n ) O(n{log_2}n) O(nlog2n) | O ( n l o g 2 n ) O(n{log_2}n) O(nlog2n) | O ( n l o g 2 n ) O(n{log_2}n) O(nlog2n) | O ( n ) O(n) O(n) | 稳定 |
2.分治算法
二分: binarySearch 又叫 折半查找 是对有单调性质的数列进行查找
二分的复杂度很低,达到了 O ( l o g n ) O({log_n}) O(logn) 的复杂度
模板1:
int lb=MIN,rb=MAX;
int ans=-1;
while(lb<=rb)
{int mid=(lb+rb)/2;if(check(mid)){ans=mid;lb=mid+1;}else{rb=mid-1;}printf("%d\n",ans);
}
模板2:
int lb=MIN,rb=MAX;
int mid;
while(l<r)
{mid=(lb+rb)/2;if(check(mid)){lb=mid;}else{rb=mid-1;}
}
return lb;
满足最小值的模板:
模板一:
int lb=MIN,rb=MAX;
int ans=-1;
while(lb<=rb)
{int mid=(lb+rb)/2;if(check(mid)){ans=mid;rb=mid-1;}else{lb=mid+1;}printf("%d\n",ans);
}
模板二:
int lb=MIN,rb=MAX;
int mid;
while(l<r)
{mid=(lb+rb)/2;if(check(mid)){rb=mid;}else{lb=mid+1;}
}
return rb;
3.倍增算法
(1)快速幂
最常见的 x y m o d m {x^y}\bmod m xymodm
typedef long long ll;
ll mypow(ll x,ll y,ll m)
{ll ans=1%m;for(;y;y>>1){if(y&1) ans=ans%x*m;x=x*x%m;}return ans;
}
5.搜索
(1)深度优先搜索
深度优先搜索算法(英语:Depth-First Search,简称DFS)是一种用于遍历或搜索树或搜索图的算法。
深度优先搜索是一种在开发爬虫早期使用较多的方法。它的目的是要达到被搜索结构的叶结点(即那些不包含任何超链的HTML文件) 。在一个HTML文件中,当一个超链被选择后,被链接的HTML文件将执行深度优先搜索,即在搜索其余的超链结果之前必须先完整地搜索单独的一条链。深度优先搜索沿着HTML文件上的超链走到不能再深入为止,然后返回到某一个HTML文件,再继续选择该HTML文件中的其他超链。当不再有其他超链可选择时,说明搜索已经结束。
代码框架:
void dfs(int k)//k:当前顶点
{if(/*找到解 或者 没有可访问的顶点*/){printf("%d",/*输出解*/);return ;}for(int i=1;i<=/*搜索分枝*/;i++){/*标记该顶点已访问*/;dfs(/*下一个顶点*/);/*还原该顶点的状态*/;}
}
(2)广度优先遍历
广度优先搜索算法(Breadth-First Search,BFS)是一种通过逐层遍历所有访问对象,从而通过最短节点数到大目标的算法。
代码框架:
void bfs()
{/*初始节点入队*/;while(/*队列非空*/){/*队头元素出队*/,/*赋给 current*/;while(/*current 还可以扩展*/){/*由节点 current 扩展出新节点 new*/;if(/*new 重复于已有的节点状态*/) continue;/*new 节点入队*/if(/*new 节点是目标状态*/){/*置 flag=true*/;break;}}}
}
6.动态规划(DP)
(1)线性动态规划
- 最大子段和
给出一段序列,选出其中连续且非空的一段使得这一段和最大。
输入格式
第一行是一个整数 n n n ,表示了序列的长度
第二行是包含 n n n 个绝对值不大于 10000 10000 10000 的整数 a i {a_i} ai ,描述了这段序列。
输出格式
一个整数,为最大的字段和是多少。
字段的最小长度为1.
样例输入
7
2 -4 3 -1 2 -4 3
样例输出
4
核心代码:
int a[N];
int dp[N];
for(int i=1;i<=n;i++)
{dp=max(dp[i-1]+a[i],a[i]);ans=max(ans,dp[i]);
}
- 最长上升子序列
一个树的序列 b i {b_i} bi ,当 b 1 < b 2 < b 3 < . . . < b s {b_1}<{b_2}<{b_3}<...<{b_s} b1<b2<b3<...<bs 的时候,我们称这个序列是上升的。
对于给定的一个序列( a 1 , a 2 , a 3 , . . . , a n {a_1},{a_2},{a_3},...,{a_n} a1,a2,a3,...,an)我们可以得到一些上升子序列 a i 1 , a i 2 , a i 3 , . . . , a i k {a_{i1}},{a_{i2}},{a_{i3}},...,{a_{ik}} ai1,ai2,ai3,...,aik ,这里 1 ≤ i 1 < i 2 < i 3 < . . . < i q ≤ N 1 \leq {i_1}<{i_2}<{i_3}<...<{i_q} \leq N 1≤i1<i2<i3<...<iq≤N
你的任务,就是对于给定的序列,求出最长上升序列的长度。
输入格式
输入的第一行是序列的长度 n ( 1 ≤ n ≤ 1000 ) n(1 \leq n \leq 1000) n(1≤n≤1000)。
第二行给出的序列中的 n n n 个整数,这些整数的取值范围都在0到10000.
输出格式
最长上升子序列的长度。
样例输入
7
1 7 3 5 9 4 8
样例输出
4
核心代码:
int a[N];
int dp[N];
for(int i=1;i<=n;i++)
{dp[i]=1;//附初值for(int j=1;j<i;j++){if(a[j]<a[i])//dp找最大值{dp[i]=max(dp[i],dp[j]+1);}}ans=max(ans,dp[i]);
}
- 最长公共子序列
给定两个字符串 x , y x,y x,y ,长度不超过5000,求出两个序列的最长公共子序列。
**注意:**子序列不是字串,不要求连续。
输入格式
第一行一个字符串,表示字符串 x x x ,第二行一个字符串,表示字符串 y y y。
输出格式
一个整数,表示最长的公共子序列长度。
样例输入
cnblogs
belong
样例输出
4
核心代码:
int c[N][N];
int len1,len2;
len1=strlen(x+1);
len2=strlen(y+1);
for(int i=1;i<=len1;i++)
{for(int j=1;j<len2;j++){if(x[i]==y[i]){c[i][j]=a[i-1][j]+1;}else{c[i][j]=max(c[i-1][j],c[i][j-1]);}}
}
(2)矩阵类动态规划
- 数字三角形
观察下面的数字金字塔。
写一个程序来查看从最高点到最低部任意处结束路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以走到右下方的点。
73 8
8 1 0
2 7 4 4
4 5 2 6 5
在上面的样例中,从 7→3→8→7→5 的路径产生了最大和,为30.
输入格式
第一行一个正整数 r r r ,表示行的数目。
后面每一行为这数字金字塔特定包含的整数。
输出格式
单独一行,包含那可能得到的最大的和。
样例输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
样例输出:
30
核心代码:
int dp[N][N];
for(int j=1;j<=r;j++)
{dp[r][j]=a[r][j];
}
for(int i=r-1;i>=1;i--)
{for(int j=1;j<=i;j++){dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+a[i][j];}
}
(3)背包问题
背包问题(Knapsack problem)可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。
背包问题又分为:01背包、完全背包、多重背包。此外,还存在一些其他考法,例如恰好装满、求方案总数、求所有的方案等。
- 01背包
01背包的特点就是一个物品要不就选,要不就不选,分别表示1和0,所以叫01背包。
用 dp[i][j] 表示将前 i i i 个物品放入载重为 j j j 的背包能获得的最大价值,w[i] 表示第 i i i 件物品的重量,v[i] 表示第 i i i 件物品的价值,则可以用一下状态转移式来表示这个过程:
当 w[i]>j (也即第 i i i 件物品不能放入载重为 j j j 的背包)时:
dp[i][j]=dp[i-1][j];
否则(也即第 i i i 件物品能放入载重为 j j j 的背包)
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
注意到 dp 数组和第 i i i 行的值更新只跟 i − 1 i-1 i−1 行有关,因此可以通过滚动数组结合反向更新的方式优化一下空间复杂度,在动态规划解题的时候这是一种常用的空间复杂度优化方式
二维写法
for(int i=1;i<=n;i++)
{for(int j=0;j<=c;j++){if(j<w[i]){dp[i][j]=dp[i-1][j];}else{dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);}}
}
滚动数组优化
for(int i=1;i<=n;i++)
{for(int j=c;j>=0;j++){if(j>=w[i]){dp[j]=max(dp[j],dp[j-w[i]]+v[i]);}}
}
- 完全背包
完全背包的特点是每个东西都可以随便拿(指数量: ∞ \infty ∞)
用 dp[i][j] 表示将前 i i i 个物品放入载重为 j j j 的背包能获得的最大价值,w[i] 表示第 i i i 件物品的重量, v[i] 表示第 i i i 个物品的价值,则可以用以下的状态转移方程式来表示这个过程:
当 w[i]>j (也即第 i i i 件物品不能放入载重为 j j j 的背包)
dp[i][j]=dp[i-1][j];
否则(也即第 i i i 件物品能放入载重为 j j j 的背包)
dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]);
注意如果用滚动数组的话,我们需要使用正向更新方式,这是唯一和上面的01背包问题的区别的地方。
二维写法
for(int i=1;i<=n;i++)
{for(int j=0;j<=c;j++){if(j>=w[i]){dp[i][j]=max(dp[i-1][j],d[i][j-w[i]]+v[i]);}else{dp[i][j]=dp[i-1][j];}}
}
滚动数组优化
for(int i=1;i<=n;i++)
{for(int j=0;j<=c;j++){if(j>=w[i]){dp[j]=max(dp[j],dp[j-w[i]]+v[i]);}}
}
- 多重背包
多重背包的特点是每种物品的数量不知一个,但有限。
用 dp[i][j] 表示将前 i i i 件物品放入载重为 j j j 的背包能获得的最大价值,w[i] 表示第 i i i 件物品的重量,v[i] 表示第 i i i 件物品的价值,s[i] 表示第 i i i 种物品的数量,则可以用以下的状态转移方程式来表示这个过程:
dp[i][j]=max(dp[i-1][j-k*w[i]]+k*v[i],0<=k<=s[i]);
在多重背包的计算中,可以使用二进制优化来减小时间复杂度。
for(int i=1;i<=n;i++)
{for(int j=0;j<=c;j++){for(int k=0;k<=s[i];k++){if(j>=k*w[i]){dp[i][j]=max(dp[i][j],dp[i-1][j-k*w[i]]+k*v[i]);}}}
}
相关文章:

排序算法概述
1.排序算法分类 **比较类算法排序:**通过比较来决定元素的时间复杂度的相对次序,由于其时间复杂度不能突破 O ( n l o g n ) O(nlogn) O(nlogn),因此也称为非线性时间比较类算法 **非比较类算法排序:**不通过比较来决定元素间的…...

ChatGPT在高等教育中的应用利弊探讨
人工智能在教育领域的应用日益广泛。2022年11月OpenAI开发的聊天机器人ChatGPT在全球范围内流传开来,其中用户数量最多的国家是美国(15.22%)。由于ChatGPT应用广泛,具有类似人类回答问题的能力,它正在成为许多学生和教育工作者的可信赖伙伴…...

Java之API详解之Runtime的详细解析
3.1 概述 Runtime表示Java中运行时对象,可以获取到程序运行时设计到的一些信息 3.2 常见方法 常见方法介绍 我们要学习的Object类中的常见方法如下所示: public static Runtime getRuntime() //当前系统的运行环境对象 public void exit(int statu…...

机器学习之softmax
Softmax是一个常用于多类别分类问题的激活函数和归一化方法。它将一个向量的原始分数(也称为 logits)转换为概率分布,使得每个类别的概率值在0到1之间,同时确保所有类别的概率之和等于1。Softmax函数的定义如下: 对于…...

npm script命令
1 串行/并行执行命令 //串行 npm-run-all text test npm run text && npm run test //并行改成& npm-run-all --parallel text test npm run text & npm run test2 传递参数 {"lint": "eslint js/*.js","lint:fix":…...

【力扣周赛】第360场周赛
【力扣周赛】第360场周赛 8015.距离原点最远的点题目描述解题思路 8022. 找出美丽数组的最小和题目描述解题思路 8015.距离原点最远的点 题目描述 描述:给你一个长度为 n 的字符串 moves ,该字符串仅由字符 ‘L’、‘R’ 和 ‘_’ 组成。字符串表示你在…...

php环境变量的配置步骤
要配置PHP的环境变量,以便在命令行中直接使用php命令,以下是一般的步骤: Windows 操作系统 下载和安装PHP:首先,你需要从PHP官方网站(https://www.php.net/downloads.php)下载适用于你的操作系…...

Kdtree
Kdtree kdtree 就是在 n 维空间对数据点进行二分;具体先确定一个根,然后小于在这个维度上的根的节点在左边,大于的在右边,再进行下一个维度的划分。直到维度结束,再重复,或者直到达到了结束条件࿱…...
算法leetcode|74. 搜索二维矩阵(rust重拳出击)
文章目录 74. 搜索二维矩阵:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 74. 搜索二维矩阵: 给你一个满足下述两条属性的…...

element浅尝辄止7:InfiniteScroll 无限滚动
滚动加载:滚动至底部时,加载更多数据。 1.如何使用? //在要实现滚动加载的列表上上添加v-infinite-scroll,并赋值相应的加载方法, //可实现滚动到底部时自动执行加载方法。<template><ul class"infinit…...

Day05-Vue基础
Day05-Vue基础 一、单向数据流 父子组件通信。会在父组件中定义好数据,将数据传递给子组件,可以使用这个数据 Vue中针对props这个属性提出了一个单向数据流的概念。 Vue针对props做了一些限制,可以接受值,使用这个值,规范中不要去直接修改这个值 目的是为了对数据流进…...
《机器学习在车险定价中的应用》实验报告
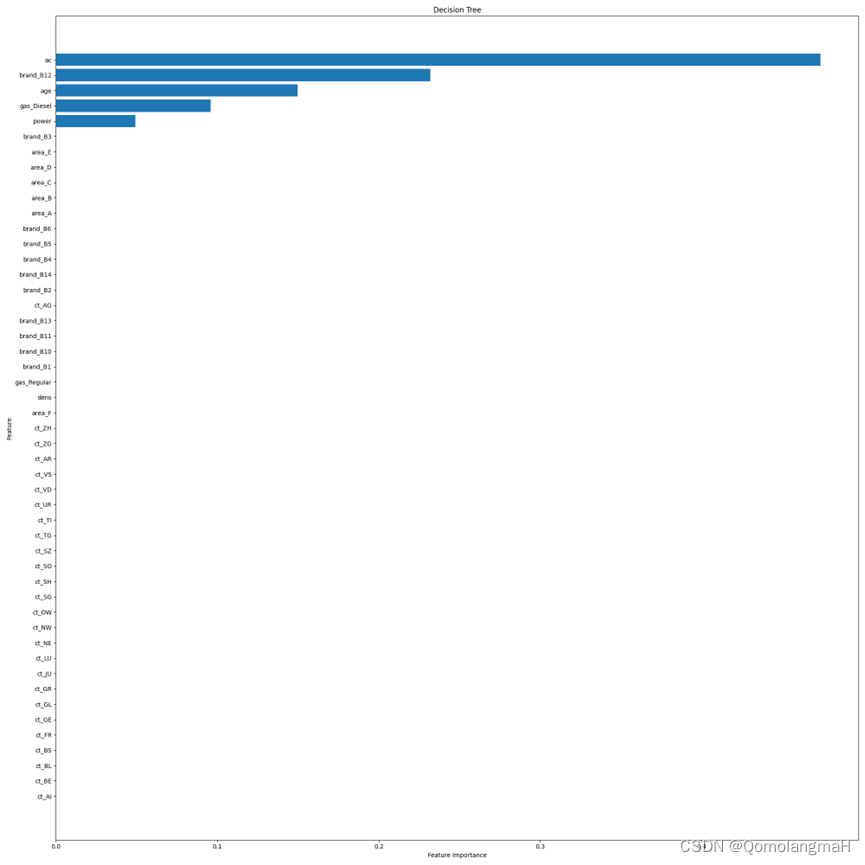
目录 一、实验题目 机器学习在车险定价中的应用 二、实验设置 1. 操作系统: 2. IDE: 3. python: 4. 库: 三、实验内容 实验前的猜想: 四、实验结果 1. 数据预处理及数据划分 独热编码处理结果(以…...
14. Docker中实现CI和CD
目录 1、前言 2、什么是CI/CD 3、部署Jenkins 3.1、下载Jenkins 3.2、启动Jenkins 3.3、访问Jenkins页面 4、Jenkins部署一个应用 5、Jenkins实现Docker应用的持续集成和部署 5.1、创建Dockerfile 5.2、集成Jenkins和Docker 6、小结 1、前言 持续集成(CI/CD)是一种…...

【多思路解决喝汽水问题】1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水
题目内容 喝汽水问题 喝汽水,1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水(编程实现)。 题目分析 数学思路分析 根据给出的问题和引用内容,我们可以得出答案。 首先ÿ…...
)
P1591 阶乘数码(Java高精度)
题目描述 求 n ! n! n! 中某个数码出现的次数。 输入格式 第一行为 t ( t ≤ 10 ) t(t \leq 10) t(t≤10),表示数据组数。接下来 t t t 行,每行一个正整数 n ( n ≤ 1000 ) n(n \leq 1000) n(n≤1000) 和数码 a a a。 输出格式 对于每组数据&a…...

Mybatis的动态SQL及关键属性和标识的区别(对SQL更灵活的使用)
( 虽然文章中有大多文本内容,想了解更深需要耐心看完,必定大有受益 ) 目录 一、动态SQL ( 1 ) 是什么 ( 2 ) 作用 ( 3 ) 优点 ( 4 ) 特殊标签 ( 5 ) 演示 二、#和$的区别 2.1 #使用 ( 1 ) #占位符语法 ( 2 ) #优点 2.…...
mysql下载
网址 MySQL :: Download MySQL Community Serverhttps://dev.mysql.com/downloads/mysql/ 2、选择MSI进行安装 3、这里我选择离线安装 4、这里我选择直接下载 5、等待下载安装即可...

聚合函数与窗口函数
聚合函数 回答一 聚合函数(Aggregate Functions)是SQL中的函数,用于对一组数据进行计算,并返回单个结果。聚合函数通常用于统计和汇总数据,包括计算总和、平均值、计数、最大值和最小值等。 以下是一些常见的聚合函…...
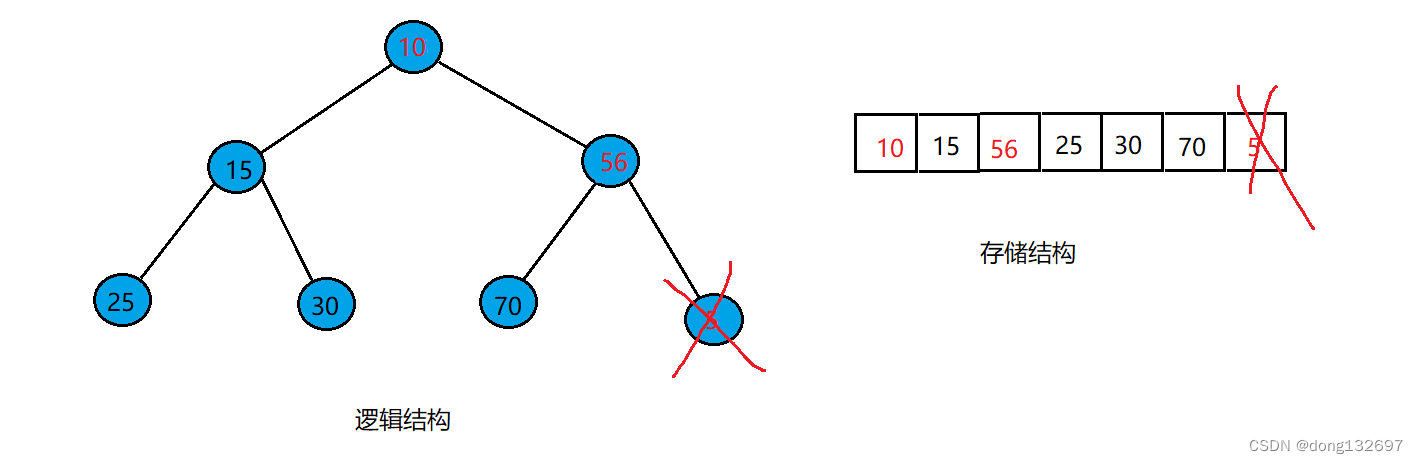
c语言实现堆
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、树1、树的概念2、树的相关概念3、树的表示 二、二叉树1、二叉树概念2、特殊的二叉树3、二叉树的性质4、二叉树的顺序结构5、二叉树的链式结构 三、堆(二叉树…...

ubuntu 如何将文件打包成tar.gz
要将文件打包成.tar.gz文件,可以使用以下命令: tar -czvf 文件名.tar.gz 文件路径 其中,-c表示创建新的归档文件,-z表示使用gzip进行压缩,-v表示显示详细的打包过程,-f表示指定归档文件的名称。 例如&am…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...
