【图论】Floyd
算法提高课笔记)
文章目录
- 例题
- 牛的旅行
- 题意
- 思路
- 代码
- 排序
- 题意
- 思路
- 代码
- 观光之旅
- 题意
- 思路
- 代码
例题
牛的旅行
原题链接
农民John的农场里有很多牧区,有的路径连接一些特定的牧区。
一片所有连通的牧区称为一个牧场。
但是就目前而言,你能看到至少有两个牧区不连通。
现在,John想在农场里添加一条路径(注意,恰好一条)。
一个牧场的直径就是牧场中最远的两个牧区的距离(本题中所提到的所有距离指的都是最短的距离)。
考虑如下的两个牧场,每一个牧区都有自己的坐标:

图 1 是有 5 个牧区的牧场,牧区用“*”表示,路径用直线表示。
图 1 所示的牧场的直径大约是 12.07106, 最远的两个牧区是 A 和 E,它们之间的最短路径是 A-B-E。
图 2 是另一个牧场。
这两个牧场都在John的农场上。
John将会在两个牧场中各选一个牧区,然后用一条路径连起来,使得连通后这个新的更大的牧场有最小的直径。
注意,如果两条路径中途相交,我们不认为它们是连通的。
只有两条路径在同一个牧区相交,我们才认为它们是连通的。
现在请你编程找出一条连接两个不同牧场的路径,使得连上这条路径后,所有牧场(生成的新牧场和原有牧场)中直径最大的牧场的直径尽可能小。
输出这个直径最小可能值。
输入格式
第 1 行:一个整数 N, 表示牧区数;
第 2 到 N+1 行:每行两个整数 X,Y, 表示 N 个牧区的坐标。每个牧区的坐标都是不一样的。
第 N+2 行到第 2*N+1 行:每行包括 N 个数字 ( 0或1 ) 表示一个对称邻接矩阵。
例如,题目描述中的两个牧场的矩阵描述如下:
A B C D E F G H
A 0 1 0 0 0 0 0 0
B 1 0 1 1 1 0 0 0
C 0 1 0 0 1 0 0 0
D 0 1 0 0 1 0 0 0
E 0 1 1 1 0 0 0 0
F 0 0 0 0 0 0 1 0
G 0 0 0 0 0 1 0 1
H 0 0 0 0 0 0 1 0
输入数据中至少包括两个不连通的牧区。
输出格式
只有一行,包括一个实数,表示所求答案。
数字保留六位小数。
数据范围
1 ≤ N ≤ 150 , 1≤N≤150, 1≤N≤150,
0 ≤ X , Y ≤ 105 0≤X,Y≤105 0≤X,Y≤105
输入样例
8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010
输出样例
22.071068
题意
给出一张图,连通的部分算作一个区域,每个区域的直径为区域中相隔最远的两个点的距离,问在不同区域中添加一条边,得到的最小直径是多少
思路
先建图,然后跑一遍floyd算出和每一个点相隔最远的点的距离
得到的最新直径一定大于等于原来的最大直径,因此可以先求出原来的最大直径maxd[i]
加上一条边[i, j]得到的新直径是maxd[i] + maxd[j] + dist[i][j]
二者取最大值即可
代码
#include <bits/stdc++.h>using namespace std;typedef pair<double, double> PDD;const int N = 155;
const double INF = 1e20;int n;
double d[N][N];
double maxd[N];
char g[N][N];
PDD q[N];double get_dist(PDD a, PDD b)
{double dx = a.first - b.first;double dy = a.second - b.second;return sqrt(dx * dx + dy * dy);
}int main()
{cin >> n;for (int i = 0; i < n; i ++ ) cin >> q[i].first >> q[i].second;for (int i = 0; i < n; i ++ ) cin >> g[i];for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )if (i == j) d[i][j] = 0;else if (g[i][j] == '1') d[i][j] = get_dist(q[i], q[j]); // ij之间有边else d[i][j] = INF; // ij之间无边// floyd更新最短路for (int k = 0; k < n; k ++ )for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )d[i][j] = min(d[i][j], d[i][k] + d[k][j]);double r1 = 0; // 两个牧场中最长的直径for (int i = 0; i < n; i ++ ){for (int j = 0; j < n; j ++ )if (d[i][j] < INF / 2) // 说明ij之间有边maxd[i] = max(maxd[i], d[i][j]); // 更新与i最远的点距离r1 = max(r1, maxd[i]); // 更新直径}double r2 = INF; // 加边之后的最长值for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )if (d[i][j] > INF / 2) // 说明ij之间无边 可以加边r2 = min(r2, maxd[i] + maxd[j] + get_dist(q[i], q[j]));printf("%.6lf\n", max(r1, r2));
}
排序
原题链接
给定 n 个变量和 m 个不等式。其中 n 小于等于 26,变量分别用前 n 的大写英文字母表示。
不等式之间具有传递性,即若 A>B 且 B>C,则 A>C。
请从前往后遍历每对关系,每次遍历时判断:
如果能够确定全部关系且无矛盾,则结束循环,输出确定的次序;
如果发生矛盾,则结束循环,输出有矛盾;
如果循环结束时没有发生上述两种情况,则输出无定解。
输入格式
输入包含多组测试数据。
每组测试数据,第一行包含两个整数 n 和 m。
接下来 m 行,每行包含一个不等式,不等式全部为小于关系。
当输入一行 0 0 时,表示输入终止。
输出格式
每组数据输出一个占一行的结果。
结果可能为下列三种之一:
- 如果可以确定两两之间的关系,则输出
Sorted sequence determined after t relations: yyy...y.,其中t指迭代次数,yyy...y是指升序排列的所有变量。 - 如果有矛盾,则输出:
Inconsistency found after t relations.,其中t指迭代次数。 - 如果没有矛盾,且不能确定两两之间的关系,则输出
Sorted sequence cannot be determined.。
数据范围
2 ≤ n ≤ 26 ,变量只可能为大写字母 A ∼ Z 。 2≤n≤26,变量只可能为大写字母 A∼Z。 2≤n≤26,变量只可能为大写字母A∼Z。
输入样例1
4 6
A<B
A<C
B<C
C<D
B<D
A<B
3 2
A<B
B<A
26 1
A<Z
0 0
输出样例1
Sorted sequence determined after 4 relations: ABCD.
Inconsistency found after 2 relations.
Sorted sequence cannot be determined.
输入样例2
6 6
A<F
B<D
C<E
F<D
D<E
E<F
0 0
输出样例2
Inconsistency found after 6 relations.
输入样例3
5 5
A<B
B<C
C<D
D<E
E<A
0 0
输出样例3
Sorted sequence determined after 4 relations: ABCDE.
题意
从前到后遍历给出的关系,如果能确定所有关系就直接输出当前次数和关系,如果前后矛盾则输出矛盾,如果得不到最终关系就输出得不到最终关系
思路
传递闭包
已知a>b b>c 一定可以推出 a>c,根据这个性质,我们可以在得到每个新的判断时进行传递,看看是否不满足原先已知的结论,如果不满足就会出现i和i的关系确定的结果
代码
#include <bits/stdc++.h>using namespace std;const int N = 26;int n, m;
bool g[N][N], d[N][N]; // 表示两个字母之间关系(前一个字母小于后一个字母)是否确定
bool st[N];void floyd()
{memcpy(d, g, sizeof d);for (int k = 0; k < n; k ++ )for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )d[i][j] |= d[i][k] && d[k][j]; // 如果有i->k k->j的边 那就加上i->j的边
}int check()
{for (int i = 0; i < n; i ++ )if (d[i][i]) return 2; // 出现矛盾返回2for (int i = 0; i < n; i ++ )for (int j = 0; j < i; j ++ )if (!d[i][j] && !d[j][i])return 0; // 遍历所有数对 没确定返回0return 1; // 确定就返回1
}char get_min()
{for (int i = 0; i < n; i ++ )if (!st[i]){bool flag = true;for (int j = 0; j < n; j ++ )if (!st[j] && d[j][i]) // 如果有没出现过的j比i还小的话说明i不是最小值{flag = false;break;}if (flag) // 否则i就是当前没出现过的数中的最小值{st[i] = true;return 'A' + i;}}
}int main()
{while (cin >> n >> m, n || m){memset(g, 0, sizeof g);int type = 0, t; // type表示目前关系未确定/确定/矛盾for (int i = 1; i <= m; i ++ ){char str[5];cin >> str;int a = str[0] - 'A', b = str[2] - 'A';if (!type){g[a][b] = 1;floyd();type = check();if (type) t = i; // t记录经过几次才确定所有关系}}if (!type) puts("Sorted sequence cannot be determined."); // 关系不确定else if (type == 2) cout << "Inconsistency found after " << t << " relations.\n"; // 矛盾else // 确定{memset(st, 0, sizeof st);cout << "Sorted sequence determined after " << t << " relations: ";for (int i = 0; i < n; i ++ ) cout << get_min();cout << ".\n";}}
}
观光之旅
原题链接
给定一张无向图,求图中一个至少包含 3 个点的环,环上的节点不重复,并且环上的边的长度之和最小。
该问题称为无向图的最小环问题。
你需要输出最小环的方案,若最小环不唯一,输出任意一个均可。
输入格式
第一行包含两个整数 N 和 M,表示无向图有 N 个点,M 条边。
接下来 M 行,每行包含三个整数 u,v,l,表示点 u 和点 v 之间有一条边,边长为 l。
输出格式
输出占一行,包含最小环的所有节点(按顺序输出),如果不存在则输出 No solution.。
数据范围
1 ≤ N ≤ 100 , 1≤N≤100, 1≤N≤100,
1 ≤ M ≤ 10000 , 1≤M≤10000, 1≤M≤10000,
1 ≤ l < 500 1≤l<500 1≤l<500
输入样例
5 7
1 4 1
1 3 300
3 1 10
1 2 16
2 3 100
2 5 15
5 3 20
输出样例
1 3 5 2
题意
无向图的最小环裸题
思路
假设环的形式是这样的:(ij均小于k)

那么环的长度就是d[i][j] + g[j][k] + g[k][i](d代表ij在图上的最短距离,g表示两点之间有边的话 边的长度)
用pos[i][j] = k记录i和j的最短路由k的状态转移,k是路径中编号最大的点
在floyd中循环每个k,如果d[i][j] + g[j][k] + g[k][i]比当前的最小环长度更小就更新一下
使用类似中序遍历的算法求出环中的字母
代码
#include <bits/stdc++.h>using namespace std;typedef long long ll;const int N = 110, INF = 0x3f3f3f3f;int n, m;
int d[N][N], g[N][N];
int pos[N][N];
int path[N], cnt;void get_path(int i, int j)
{if (pos[i][j] == 0) return;// 类似于中序遍历int k = pos[i][j];get_path(i, k);path[cnt ++ ] = k;get_path(k, j);
}int main()
{cin >> n >> m;memset(g, 0x3f3f3f3f, sizeof g);for (int i = 1; i <= n; i ++ ) g[i][i] = 0; // 避免统计自环while (m -- ){int a, b, c;cin >> a >> b >> c;g[a][b] = g[b][a] = min(g[a][b], c);}int res = INF;memcpy(d, g, sizeof d);for (int k = 1; k <= n; k ++ ){for (int i = 1; i < k; i ++ )for (int j = i + 1; j < k; j ++ )if ((ll)d[i][j] + g[j][k] + g[k][i] < res) // 一旦发现比原来的最短路还要短的路径就更新{res = d[i][j] + g[j][k] + g[k][i]; // 最短路长度// 更新最短路中的点cnt = 0;path[cnt ++ ] = k;path[cnt ++ ] = i;get_path(i, j);path[cnt ++ ] = j;}// 更新两点之间的距离 在更新完最小环之后更新所以不会对最小环有影响for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )if (d[i][j] > d[i][k] + d[k][j]){d[i][j] = d[i][k] + d[k][j];pos[i][j] = k;}}if (res == INF) puts("No solution.");else{for (int i = 0; i < cnt; i ++ ) cout << path[i] << ' ';cout << '\n';}
}
相关文章:

【图论】Floyd
算法提高课笔记) 文章目录 例题牛的旅行题意思路代码 排序题意思路代码 观光之旅题意思路代码 例题 牛的旅行 原题链接 农民John的农场里有很多牧区,有的路径连接一些特定的牧区。 一片所有连通的牧区称为一个牧场。 但是就目前而言,你…...
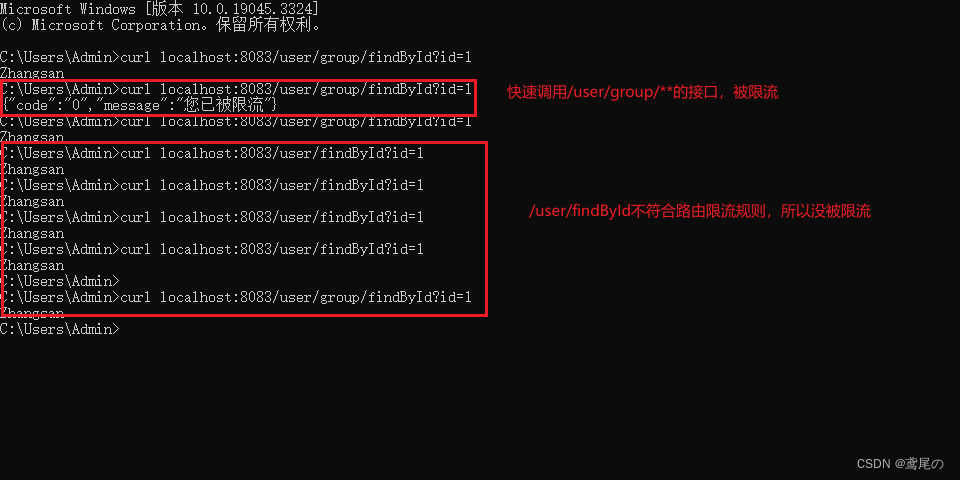
SpringCloudAlibaba Gateway(三)-整合Sentinel功能路由维度、API维度进行流控
Gateway整合Sentinel 前面使用过Sentinel组件对服务提供者、服务消费者进行流控、限流等操作。除此之外,Sentinel还支持对Gateway、Zuul等主流网关进行限流。 自sentinel1.6.0版开始,Sentinel提供了Gateway的适配模块,能针对路由(rou…...

【笔试强训选择题】Day38.习题(错题)解析
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:笔试强训选择题 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!! 文章目录 前言一、Day…...
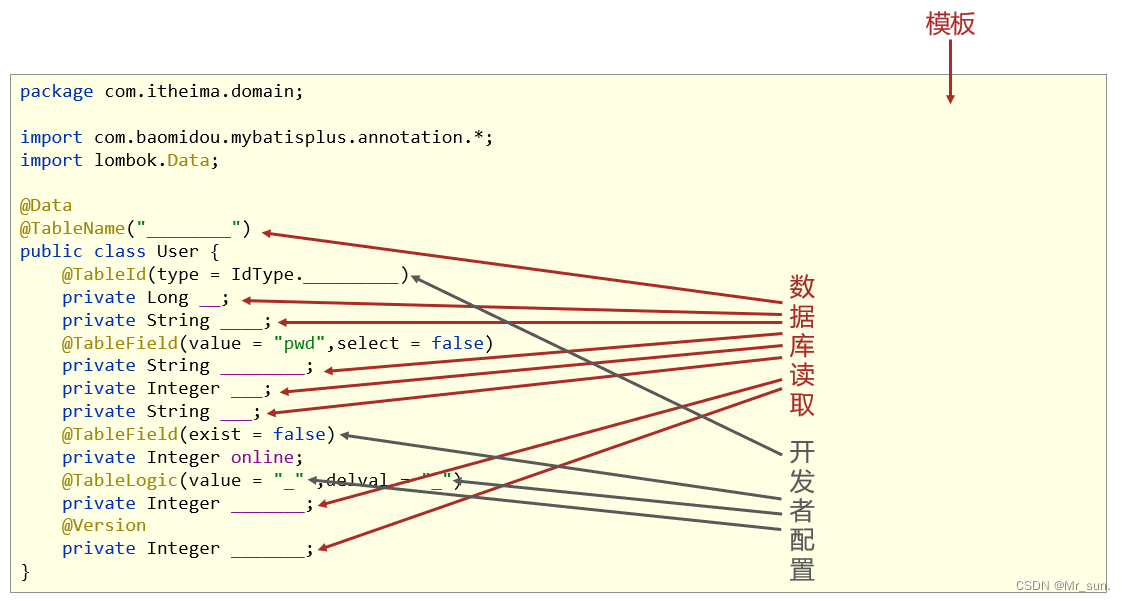
DAY08_MyBatisPlus——入门案例标准数据层开发CRUD-Lombok-分页功能DQL编程控制DML编程控制乐观锁快速开发-代码生成器
目录 一 MyBatisPlus简介1. 入门案例问题导入1.1 SpringBoot整合MyBatisPlus入门程序①:创建新模块,选择Spring初始化,并配置模块相关基础信息②:选择当前模块需要使用的技术集(仅保留JDBC)③:手…...

分光棱镜BS、PB、NPBS的区别
BS(分光棱镜):对入射偏振敏感,线偏振角度会影响分光比。若入射的是自然光或圆偏振光,则按50:50分光。分束的时候只管分能量,理想器件下出射的两路光偏振态还是原来的样子,实际工艺缺…...
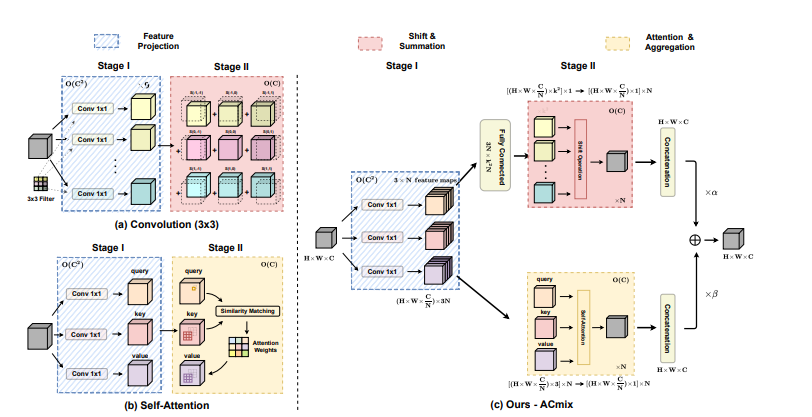
人工智能论文通用创新点(一)——ACMIX 卷积与注意力融合、GCnet(全局特征融合)、Coordinate_attention、SPD(可替换下采样)
1.ACMIX 卷积与注意力融合 论文地址:https://arxiv.org/pdf/2111.14556.pdf 为了实现卷积与注意力的融合,我们让特征图经过两个路径,一个路径经过卷积,另外一个路径经过Transformer,但是,现在有一个问题,卷积路径比较快,Transformer比较慢。因此,我们让Q,K,V通过1*1的…...

您的计算机已被[new_day@torguard.tg].faust 勒索病毒感染?恢复您的数据的方法在这里!
导言: 随着科技的迅速发展,网络空间也变得越来越危险,而勒索病毒则是网络威胁中的一个严重问题。 [ new_daytorguard.tg ].faust 勒索病毒是最新的威胁之一,采用高度复杂的加密技术,将受害者的数据文件锁定,…...

18--Elasticsearch
一 Elasticsearch介绍 1 全文检索 Elasticsearch是一个全文检索服务器 全文检索是一种非结构化数据的搜索方式 结构化数据:指具有固定格式固定长度的数据,如数据库中的字段。 非结构化数据:指格式和长度不固定的数据,如电商网站…...

代码随想录算法训练营 day59|503.下一个更大元素II、42. 接雨水
一、503.下一个更大元素II 力扣题目链接 可以不扩充nums,在遍历的过程中模拟走两边nums class Solution { public:vector<int> nextGreaterElements(vector<int>& nums) {vector<int> result(nums.size(), -1);if (nums.size() 0) return…...

MyBatis数据库操作
文章目录 前言一、MyBatis的各种查询功能1.查询一个实体类对象2.查询一个List集合3.查询单个数据4.查询一条数据为map集合5.查询多条数据为map集合方法一方法二 6.测试类 二、特殊SQL的执行1.模糊查询2.批量删除3.动态设置表名5.添加功能获取自增的主键6.测试类 三、自定义映射…...

python flask框架 debug功能
从今天开始,准备整理一些基础知识,分享给需要的人吧 先整理个flask的debug功能,首先列举一下debug加与不加的区别,然后再上代码和图看看差异 区别: (1)加了debug后,修改js…...

《深入浅出OCR》第六章:OCR数据集与评价指标
一、OCR技术流程 在介绍OCR数据集开始,我将带领大家和回顾下OCR技术流程,典型的OCR技术pipline如下图所示,其中,文本检测和识别是OCR技术的两个重要核心技术。 1.1 图像预处理: 图像预处理是OCR流程的第一步…...
15. 线性代数 - 克拉默法则
文章目录 克拉默法则矩阵运算Hi,大家好。我是茶桁。 上节课我们在最后提到了一个概念「克拉默法则」,本节课,我们就来看看到底什么是克拉默法则。 克拉默法则 之前的课程我们一直在强调,矩阵是线性方程组抽象的来的。那么既然我们抽象出来了,有没有一种比较好的办法高效…...
【LeetCode】剑指 Offer <二刷>(6)
目录 题目:剑指 Offer 12. 矩阵中的路径 - 力扣(LeetCode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 13. 机器人的运动范围 - 力扣&#…...
jsp页面出现“String cannot be resolved to a type”错误解决办法
篇首语:小编为大家整理,主要介绍了jsp页面出现“String cannot be resolved to a type”错误解决办法相关的知识,希望对你有一定的参考价值。 jsp页面出现“String cannot be resolved to a type”错误解决办法 解决办法: 右键项目…...

【go-zero】使用自带Redis方法
yaml配置文件 RedisS:Host: Type: Pass: config增加 RedisS struct {Host stringType stringPass string}svc文件 type * struct {RedisClient *redis.Redis } func *(c config.Config) * {sqlConn : sqlx.NewMysql(c.DB.DataSource)return &*{RedisClient: redis.New(c…...
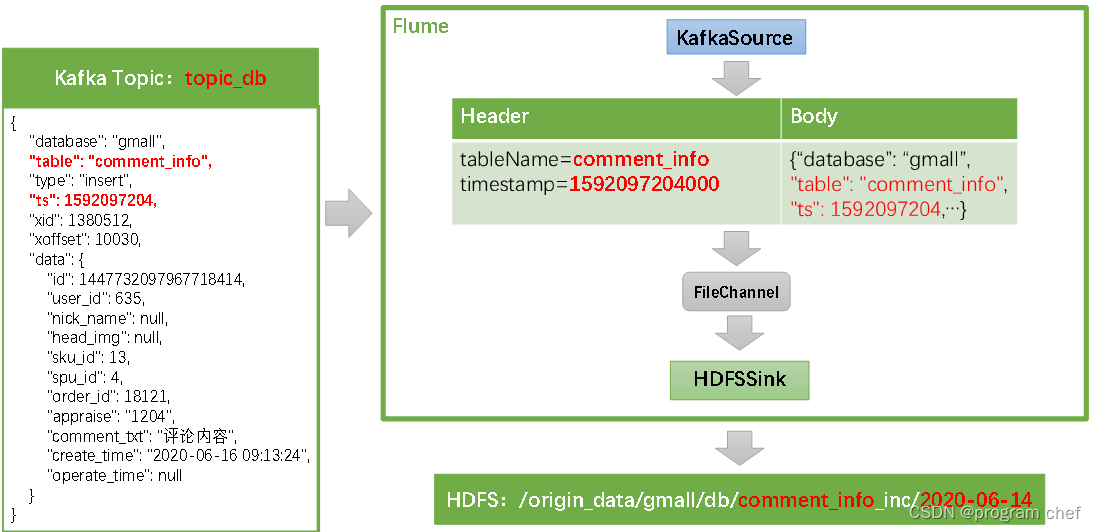
离线数仓同步数据3
业务数据_增量表数据同步 1)Flume配置概述2)Flume配置实操3)通道测试4)编写Flume启停脚本 1)Flume配置概述 Flume需要将Kafka中topic_db主题的数据传输到HDFS,故其需选用KafkaSource以及HDFSSinkÿ…...
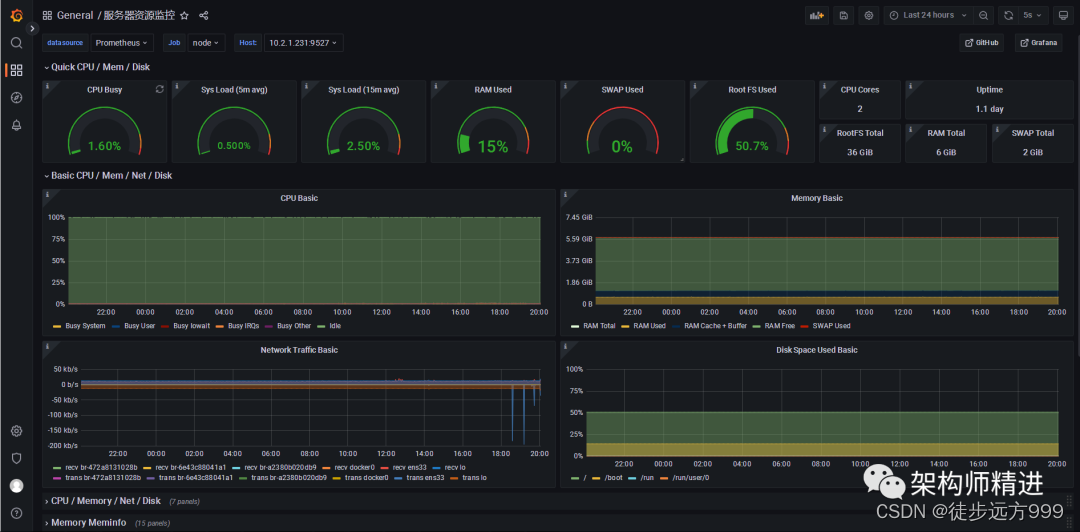
Prometheus+Grafana 搭建应用监控系统
一、背景 完善的监控系统可以提高应用的可用性和可靠性,在提供更优质服务的前提下,降低运维的投入和工作量,为用户带来更多的商业利益和客户体验。下面就带大家彻底搞懂监控系统,使用Prometheus Grafana搭建完整的应用监控系统。 …...

Spring Boot整合Log4j2.xml的问题
文章目录 问题解决参考 问题 Spring Boot整合Log4j2.xml的时候返回以下错误: Caused by: org.apache.logging.log4j.LoggingException: log4j-slf4j-impl cannot be present with log4j-to-slf4j 进行了解决。 解决 Spring Boot整合Log4j2.xml经过以下操作&#…...
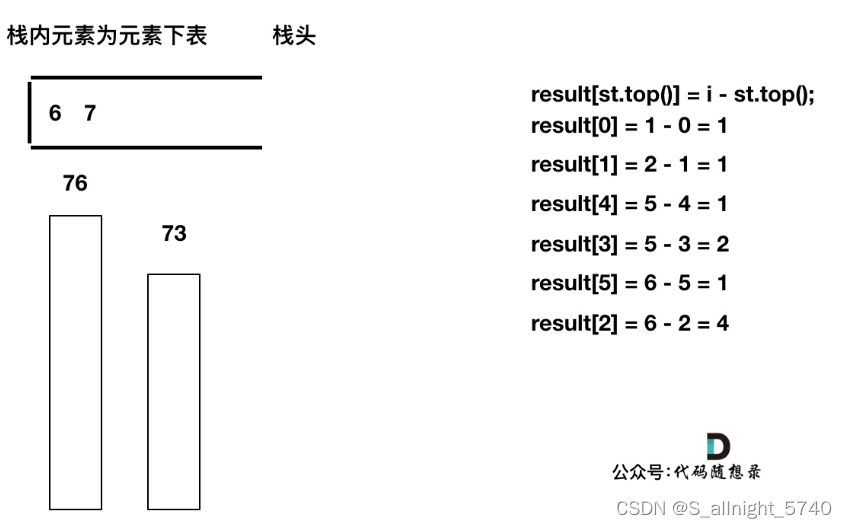
代码随想录算法训练营第五十八天 | 739. 每日温度,496.下一个更大元素 I
代码随想录算法训练营第五十八天 | 739. 每日温度,496.下一个更大元素 I 739. 每日温度496.下一个更大元素 I 739. 每日温度 题目链接 视频讲解 给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answe…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...
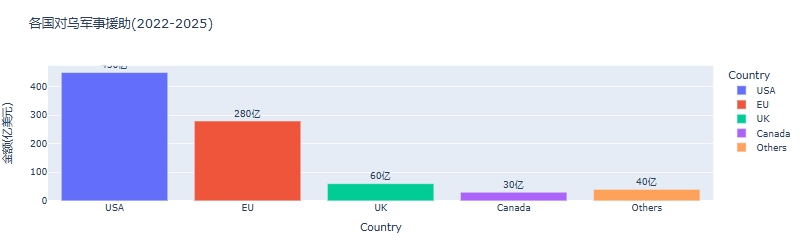
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...
