【c++】搜索二叉树的模拟实现
搜索二叉树的模拟实现
k模型完整代码
#pragma once
namespace hqj1
{template<class K>struct SBTreeNode{public://这里直接用匿名对象作为缺省参数SBTreeNode(const K& key = K()):_key(key), _cleft(nullptr), _cright(nullptr){}public:K _key;SBTreeNode* _cleft;SBTreeNode* _cright;};template<class K>class SBTree{typedef SBTreeNode<K> Node;public:SBTree():_root(nullptr){}bool Insert(const K& key){if (_root == nullptr)_root = new Node(key);else{Node* cur = _root;Node* parent = nullptr;//找到要插入的位置while (cur){parent = cur;if (cur->_key < key)cur = cur->_cright;else if (cur->_key > key)cur = cur->_cleft;elsereturn false;}//连接cur = new Node(key);if (parent->_key < key)parent->_cright = cur;elseparent->_cleft = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;elsebreak;}return cur;}bool Erase(const K& key){if (_root == nullptr)return false;else{//找出要删除元素的位置,复用查找函数也行Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key == key)break;parent = cur;if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;}//对根进行特判if (parent == nullptr){if (cur->_cleft == nullptr && cur->_cright == nullptr){delete _root;_root = nullptr;}else if (cur->_cleft == nullptr)_root = _root->_cright;else_root = _root->_cleft;return true;}//对不同情况进行处理//第一种是要删除的元素不在树内if (cur == nullptr)return false;else if (cur->_cleft == nullptr && cur->_cleft == cur->_cright){//要删除的元素是叶子节点,直接删if (cur == parent->_cleft)parent->_cleft = nullptr;elseparent->_cright = nullptr;delete cur;}else if (cur->_cleft == nullptr){//有右子树但没有左子树if (cur == parent->_cleft)parent->_cleft = cur->_cright;elseparent->_cright = cur->_cright;delete cur;}else if (cur->_cright == nullptr){//有左子树但没有右子树if (cur == parent->_cleft){parent->_cleft = cur->_cleft;}else{parent->_cright = cur->_cleft;}delete cur;}else{//既有左子树又有右子树//找左子树的最右,或者找右子树的最左节点来替换掉当前要删除的节点Node* curRL = cur->_cright;Node* parentRL = cur;while (curRL->_cleft){parentRL = curRL;curRL = curRL->_cleft;}//交换要删除的值和要删除节点的右树最左节点的值swap(cur->_key, curRL->_key);//判断要删除的节点在其父节点的位置//操控父节点指针//有一个性质:右子树中的最左节点一定没有左子树,我们让父节点连接要删除节点的右子树就行if (curRL == parentRL->_cleft)parentRL->_cleft = curRL->_cright;elseparentRL->_cright = curRL->_cright;delete curRL;curRL = nullptr;}return true;}}void InOrder(){_InOrder(_root);}private:void _InOrder(const Node* root){if (root == nullptr)return;_InOrder(root->_cleft);cout << root->_key << ' ';_InOrder(root->_cright);}Node* _root;};
}
k模型节点的定义
-
这是一个模板类,模板类型为K,代表着关键词
-
成员为:关键词、左子树指针、右子树指针
-
构造函数的参数为K类型的对象,缺省参数为匿名对象(K()),使我们代码的通用性增强
template<class K>struct SBTreeNode{public://这里直接用匿名对象作为缺省参数SBTreeNode(const K& key = K()):_key(key), _cleft(nullptr), _cright(nullptr){}public:K _key;SBTreeNode* _cleft;SBTreeNode* _cright;};
k模型二叉搜索树类的实现
-
首先将节点类类型重定义为Node方便我们后续的使用
-
成员函数为插入、删除、查找、中序遍历
-
私有成员为节点指针_root
template<class K>class SBTree{typedef SBTreeNode<K> Node;public:SBTree():_root(nullptr){}bool Insert(const K& key){if (_root == nullptr)_root = new Node(key);else{Node* cur = _root;Node* parent = nullptr;//找到要插入的位置while (cur){parent = cur;if (cur->_key < key)cur = cur->_cright;else if (cur->_key > key)cur = cur->_cleft;elsereturn false;}//连接cur = new Node(key);if (parent->_key < key)parent->_cright = cur;elseparent->_cleft = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;elsebreak;}return cur;}bool Erase(const K& key){if (_root == nullptr)return false;else{//找出要删除元素的位置,复用查找函数也行Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key == key)break;parent = cur;if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;}//对根进行特判if (parent == nullptr){if (cur->_cleft == nullptr && cur->_cright == nullptr){delete _root;_root = nullptr;}else if (cur->_cleft == nullptr)_root = _root->_cright;else_root = _root->_cleft;return true;}//对不同情况进行处理//第一种是要删除的元素不在树内if (cur == nullptr)return false;else if (cur->_cleft == nullptr && cur->_cleft == cur->_cright){//要删除的元素是叶子节点,直接删if (cur == parent->_cleft)parent->_cleft = nullptr;elseparent->_cright = nullptr;delete cur;}else if (cur->_cleft == nullptr){//有右子树但没有左子树if (cur == parent->_cleft)parent->_cleft = cur->_cright;elseparent->_cright = cur->_cright;delete cur;}else if (cur->_cright == nullptr){//有左子树但没有右子树if (cur == parent->_cleft){parent->_cleft = cur->_cleft;}else{parent->_cright = cur->_cleft;}delete cur;}else{//既有左子树又有右子树//找左子树的最右,或者找右子树的最左节点来替换掉当前要删除的节点Node* curRL = cur->_cright;Node* parentRL = cur;while (curRL->_cleft){parentRL = curRL;curRL = curRL->_cleft;}//交换要删除的值和要删除节点的右树最左节点的值swap(cur->_key, curRL->_key);//判断要删除的节点在其父节点的位置//操控父节点指针//有一个性质:右子树中的最左节点一定没有左子树,我们让父节点连接要删除节点的右子树就行if (curRL == parentRL->_cleft)parentRL->_cleft = curRL->_cright;elseparentRL->_cright = curRL->_cright;delete curRL;curRL = nullptr;}return true;}}void InOrder(){_InOrder(_root);}private:void _InOrder(const Node* root){if (root == nullptr)return;_InOrder(root->_cleft);cout << root->_key << ' ';_InOrder(root->_cright);}Node* _root;};
构造函数
-
将_root指针初始化为空指针即可
SBTree():_root(nullptr){}
Insert函数
-
Insert函数的参数为要插入的关键字
-
首先进行判空,如果_root为空,说明此时还没有节点,我们直接给_root赋值就行
-
如果不为空,那么就需要先找到要插入的位置,我们定义cur和parent两个节点指针,cur负责寻找要插入的位置,parent负责记录cur的父亲节点,由于搜索二叉树的特性,当key值大于cur所指向节点的_key值说明要插入的位置再cur节点的右子树中,反之则在cur的左子树中,通过循环来达到目的,更新cur的同时要更新parent
-
如果遇到cur的_key和key相等的情况说明插入失败,其余情况皆为插入成功
bool Insert(const K& key){if (_root == nullptr)_root = new Node(key);else{Node* cur = _root;Node* parent = nullptr;//找到要插入的位置while (cur){if (cur->_key == key)return false;parent = cur;if (cur->_key < key)cur = cur->_cright;else if (cur->_key > key)cur = cur->_cleft;}//连接cur = new Node(key);if (parent->_key < key)parent->_cright = cur;elseparent->_cleft = cur;}return true;}
Find函数
-
Find的参数为要查找的关键字
-
我们定义cur指针来找到目标节点位置,当key > cur->_key时cur要往其右子树寻找,反之则去其左子树寻找,当相等时或者cur指向空(意味着没找到)结束循环,返回cur
Node* Find(const K& key){Node* cur = _root;while (cur){if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;elsebreak;}return cur;}Erase函数
-
该函数的参数为要删除的关键字
-
当要操作的树为空树时,直接返回失败
-
不是空树则首先找出要删除节点的位置,同样是定义cur和parent节点指针,cur负责找出要删除节点的位置,parent负责记录cur节点的父节点。利用循环结构实现,循环的结束条件为cur为空指针或者找到对应位置,若为空则说明要删除节点不在树内,直接返回失败
-
找到之后首先判断是否要操作_root指针,当parent为空时说明要操作根节点,对于根节点的不同类型进行对应的操作1. 如果整棵树只有一个节点,直接删除根节点,并将根节点置为空。2. 如果根节点没有左子树,则用右子树的根节点作为新的整棵树的根节点。3. 如果根节点没有右子树,则用左子树的根节点作为新的整棵树的根节点。4. 如果根节点既有左子树又有右子树,则当作普通节点处理(见下一点的第4小点)
-
处理完根节点问题后就改判断要删除的节点是哪种类型:1. 删除节点是叶子结点,那么我们直接删除该节点并更新其父亲节点的指针(判断要删除节点是其父情节点的左子树还是右子树,操作对应的指针)2. 有右子树但没有左子树,让其父亲的对应指针指向其右子树,并删除当前节点。3. 有左子树但没有右子树,让其父亲的对应指针指向其左子树,并删除该节点4. 既有左子树又有右子树,定义curRL负责寻找其右子树的最左节点(也就是右子树的最小节点)或者定义curLR左子树的最右节点(也就是左子树的最大节点),定义parentRL记录其父亲节点,与当前节点(cur)的值进行交换,交换完后令parentRL的对应指针指向curRL的右子树,并删除curRL所指向的节点。
-
所有过程走完后返回状态(成功或者失败)
bool Erase(const K& key){if (_root == nullptr)return false;else{//找出要删除元素的位置,复用查找函数也行Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key == key)break;parent = cur;if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;}//对根进行特判if (parent == nullptr){if (cur->_cleft == nullptr && cur->_cright == nullptr){delete _root;_root = nullptr;}else if (cur->_cleft == nullptr)_root = _root->_cright;else_root = _root->_cleft;return true;}//对不同情况进行处理//第一种是要删除的元素不在树内if (cur == nullptr)return false;else if (cur->_cleft == nullptr && cur->_cleft == cur->_cright){//要删除的元素是叶子节点,直接删if (cur == parent->_cleft)parent->_cleft = nullptr;elseparent->_cright = nullptr;delete cur;}else if (cur->_cleft == nullptr){//有右子树但没有左子树if (cur == parent->_cleft)parent->_cleft = cur->_cright;elseparent->_cright = cur->_cright;delete cur;}else if (cur->_cright == nullptr){//有左子树但没有右子树if (cur == parent->_cleft){parent->_cleft = cur->_cleft;}else{parent->_cright = cur->_cleft;}delete cur;}else{//既有左子树又有右子树//找左子树的最右,或者找右子树的最左节点来替换掉当前要删除的节点Node* curRL = cur->_cright;Node* parentRL = cur;while (curRL->_cleft){parentRL = curRL;curRL = curRL->_cleft;}//交换要删除的值和要删除节点的右树最左节点的值swap(cur->_key, curRL->_key);//判断要删除的节点在其父节点的位置//操控父节点指针//有一个性质:右子树中的最左节点一定没有左子树,我们让父节点连接要删除节点的右子树就行if (curRL == parentRL->_cleft)parentRL->_cleft = curRL->_cright;elseparentRL->_cright = curRL->_cright;delete curRL;curRL = nullptr;}return true;}}
kv模型完整代码
#pragma once
namespace hqj2
{template<class K, class V>struct SBTreeNode{public:SBTreeNode(const K& key = K(), const V& value = V()):_cleft(nullptr), _cright(nullptr), _key(key), _value(value){}public:SBTreeNode* _cleft;SBTreeNode* _cright;K _key;V _value;};template<class K, class V>class SBTree{typedef SBTreeNode<K, V> Node;public:SBTree():_root(nullptr){}public:bool Insert(const K& key, const V& value){if (_root == nullptr)_root = new Node(key, value);else{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key == key)return false;parent = cur;if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;}cur = new Node(key, value);if (cur == parent->_cleft)parent->_cleft = cur;elseparent->_cright = cur;}return true;}void InOrder(){_Inorder(_root);}Node*& Find(const K& key){Node* cur = _root;while (cur){if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;elsebreak;}return cur;}bool Erase(const K& key){if (_root == nullptr)return false;Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key == key)break;parent = cur;if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;}if (parent == nullptr){if (cur->_cleft == nullptr && cur->_cright == nullptr){delete _root;_root = nullptr;}else if (cur->_cleft == nullptr)_root = _root->_cright;else_root = _root->_cleft;return true;}if (cur->_cleft == nullptr && cur->_cright == nullptr){if (cur == parent->_cleft)parent->_cleft = nullptr;elseparent->_cright = nullptr;delete cur;}else if (cur->_cleft == nullptr){if (cur == parent->_cleft)parent->_cleft = cur->_cright;elseparent->_cright = cur->_cright;delete cur;}else if (cur->_cright == nullptr){if (cur == parent->_cleft)parent->_cleft = cur->_cleft;elseparent->_cright = cur->_cleft;}else{Node* parntRL = nullptr;Node* curRL = cur->_cright;while (curRL->_cleft != nullptr){parntRL = curRL;curRL = curRL->_cleft;}swap(curRL->_key, cur->_key);if (curRL == parntRL->_cleft)parntRL->_cleft = curRL->_cright;elseparntRL->_cright = curRL->_cright;delete curRL;}return true;}private:void _Inorder(const Node* root){if (root == nullptr)return;_Inorder(root->_cleft);cout << root->_key << ' ' << root->_value << ' ' << endl;_Inorder(root->_cright);}Node* _root;};
}
kv模型搜索二叉树的定义
-
是模板类,模板参数是K和V
-
成员函数和k模型一模一样
template<class K, class V>class SBTree{typedef SBTreeNode<K, V> Node;public:SBTree():_root(nullptr){}public:bool Insert(const K& key, const V& value){if (_root == nullptr)_root = new Node(key, value);else{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key == key)return false;parent = cur;if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;}cur = new Node(key, value);if (cur == parent->_cleft)parent->_cleft = cur;elseparent->_cright = cur;}return true;}void InOrder(){_Inorder(_root);}Node*& Find(const K& key){Node* cur = _root;while (cur){if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;elsebreak;}return cur;}bool Erase(const K& key){if (_root == nullptr)return false;Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key == key)break;parent = cur;if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;}if (parent == nullptr){if (cur->_cleft == nullptr && cur->_cright == nullptr){delete _root;_root = nullptr;}else if (cur->_cleft == nullptr)_root = _root->_cright;else_root = _root->_cleft;return true;}if (cur->_cleft == nullptr && cur->_cright == nullptr){if (cur == parent->_cleft)parent->_cleft = nullptr;elseparent->_cright = nullptr;delete cur;}else if (cur->_cleft == nullptr){if (cur == parent->_cleft)parent->_cleft = cur->_cright;elseparent->_cright = cur->_cright;delete cur;}else if (cur->_cright == nullptr){if (cur == parent->_cleft)parent->_cleft = cur->_cleft;elseparent->_cright = cur->_cleft;}else{Node* parntRL = nullptr;Node* curRL = cur->_cright;while (curRL->_cleft != nullptr){parntRL = curRL;curRL = curRL->_cleft;}swap(curRL->_key, cur->_key);if (curRL == parntRL->_cleft)parntRL->_cleft = curRL->_cright;elseparntRL->_cright = curRL->_cright;delete curRL;}return true;}private:void _Inorder(const Node* root){if (root == nullptr)return;_Inorder(root->_cleft);cout << root->_key << ' ' << root->_value << ' ' << endl;_Inorder(root->_cright);}Node* _root;};
kv模型节点的定义
-
节点是模板类,模板参数为K和V
-
成员为左子树指针、右子树指针、关键字、所对应的值
-
依然以匿名对象作为缺省参数,使得我们程序更加通用
template<class K, class V>struct SBTreeNode{public:SBTreeNode(const K& key = K(), const V& value = V()):_cleft(nullptr), _cright(nullptr), _key(key), _value(value){}public:SBTreeNode* _cleft;SBTreeNode* _cright;K _key;V _value;};
Insert函数
-
该函数参数为关键字、值
-
首先判断该树有无节点,无节点则直接给_root赋值,有节点则先找要插入的位置,插入的同时改变其父亲节点所对应的指针
-
返回值为插入状态
bool Insert(const K& key, const V& value){if (_root == nullptr)_root = new Node(key, value);else{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key == key)return false;parent = cur;if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;}cur = new Node(key, value);if (cur == parent->_cleft)parent->_cleft = cur;elseparent->_cright = cur;}return true;}
Find函数
-
和k模型的一模一样,不做赘述
Node*& Find(const K& key){Node* cur = _root;while (cur){if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;elsebreak;}return cur;}
Erase函数
-
和k模型的一模一样,不做赘述
bool Erase(const K& key){if (_root == nullptr)return false;Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key == key)break;parent = cur;if (key > cur->_key)cur = cur->_cright;else if (key < cur->_key)cur = cur->_cleft;}if (parent == nullptr){if (cur->_cleft == nullptr && cur->_cright == nullptr){delete _root;_root = nullptr;}else if (cur->_cleft == nullptr)_root = _root->_cright;else_root = _root->_cleft;return true;}if (cur->_cleft == nullptr && cur->_cright == nullptr){if (cur == parent->_cleft)parent->_cleft = nullptr;elseparent->_cright = nullptr;delete cur;}else if (cur->_cleft == nullptr){if (cur == parent->_cleft)parent->_cleft = cur->_cright;elseparent->_cright = cur->_cright;delete cur;}else if (cur->_cright == nullptr){if (cur == parent->_cleft)parent->_cleft = cur->_cleft;elseparent->_cright = cur->_cleft;}else{Node* parntRL = nullptr;Node* curRL = cur->_cright;while (curRL->_cleft != nullptr){parntRL = curRL;curRL = curRL->_cleft;}swap(curRL->_key, cur->_key);if (curRL == parntRL->_cleft)parntRL->_cleft = curRL->_cright;elseparntRL->_cright = curRL->_cright;delete curRL;}return true;}
相关文章:

【c++】搜索二叉树的模拟实现
搜索二叉树的模拟实现 k模型完整代码 #pragma once namespace hqj1 {template<class K>struct SBTreeNode{public://这里直接用匿名对象作为缺省参数SBTreeNode(const K& key K()):_key(key), _cleft(nullptr), _cright(nullptr){}public:K _key;SBTreeNode* _cle…...
)
Kubeadm - K8S1.20 - 高可用集群部署(博客)
这里写目录标题 Kubeadm - K8S1.20 - 高可用集群部署一.环境准备1.系统设置 二.所有节点安装docker三.所有节点安装kubeadm,kubelet和kubectl1.定义kubernetes源2.高可用组件安装、配置 四.部署K8S集群五.问题解决1.加入集群的 Token 过期2.master节点 无法部署非系…...
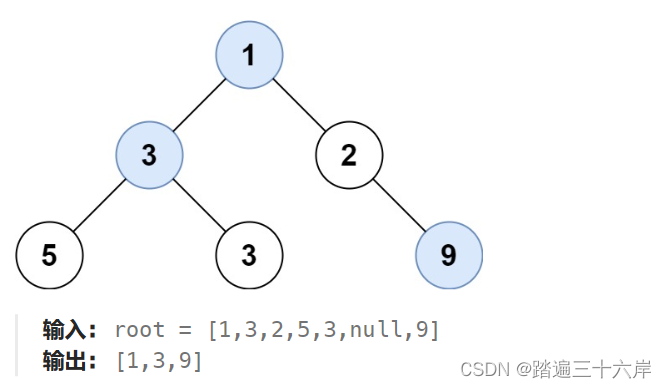
515. 在每个树行中找最大值
描述 : 给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。 题目 : LeetCode 在每个树行中找最大值 : 515. 在每个树行中找最大值 分析 : 这里其实就是在得到一层之后使用一个变量来记录当前得到的最大值 , 懂了前面的几道这就是小菜 解析 : /…...
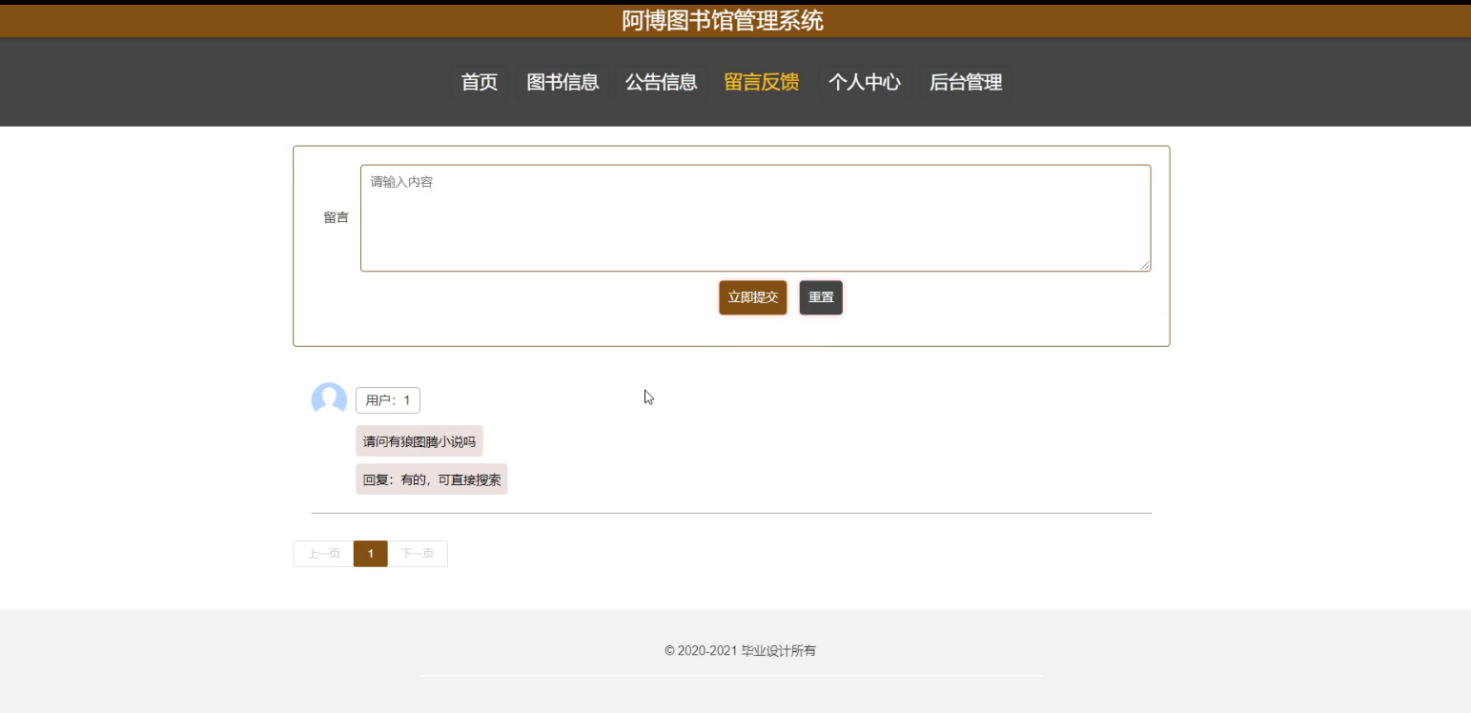
基于springboot+vue的图书馆管理系统
图书馆管理系统 springboot32阿博图书馆管理系统 源码合集: www.yuque.com/mick-hanyi/javaweb 源码下载:博主私 摘 要 随着社会的发展,计算机的优势和普及使得阿博图书馆管理系统的开发成为必需。阿博图书馆管理系统主要是借助计算机&…...

诊断刷写流程中使用到的诊断服务
10 01:诊断刷写完成后让目标ECU重置或让整车网络中其他ECU切换回默认会话 10 02:设置外部编程请求标志位或切换到编程会话(诊断刷写需要在编程会话下进行) 10 03:让目标ECU切换到扩展会话,以便进行其他诊断…...
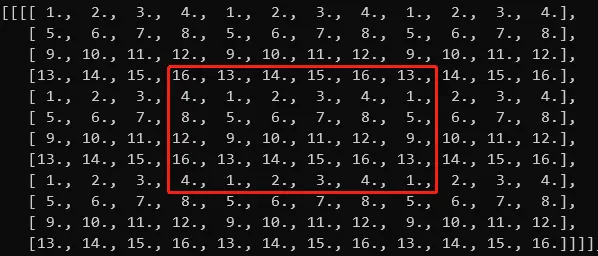
pytorch 中 nn.Conv2d 解释
1. pytorch nn.Con2d 中填充模式 torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride1, padding0, dilation1, groups1, biasTrue, padding_mode‘zeros’, deviceNone, dtypeNone) 1.1 padding 参数的含义 首先 ,padd N, 代表的是 分别在 上下&…...
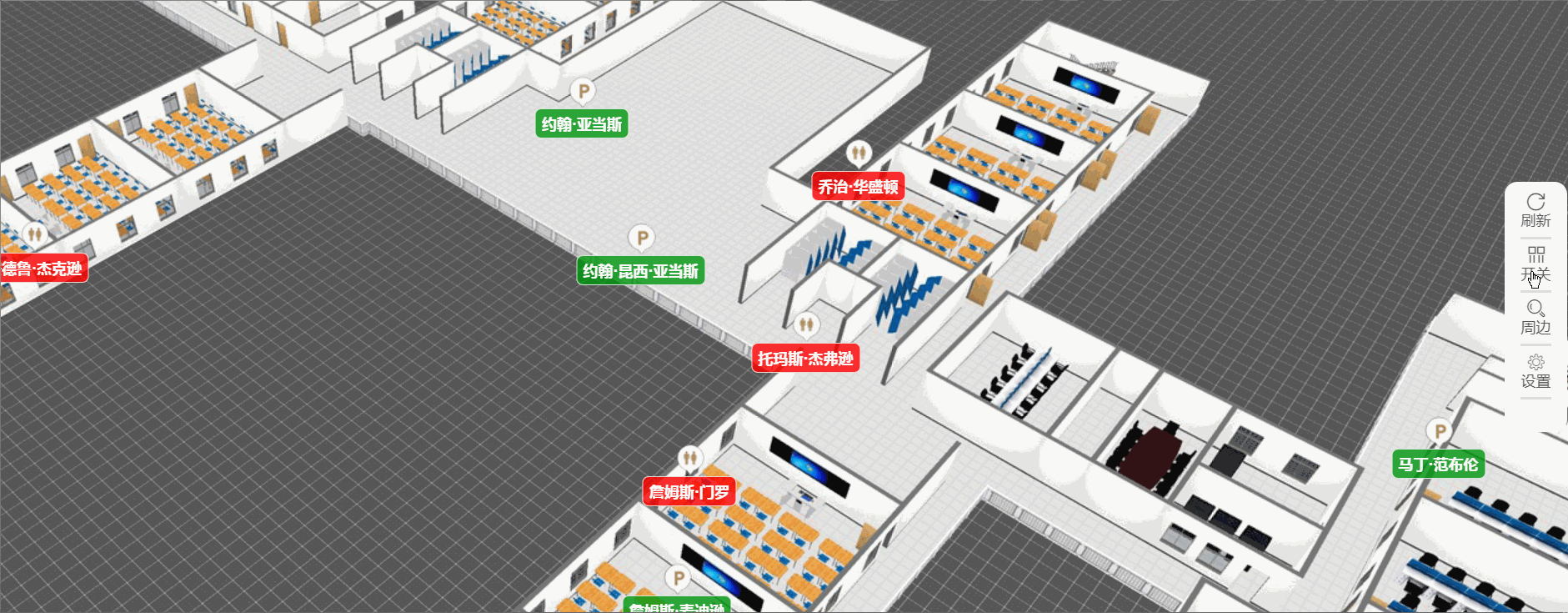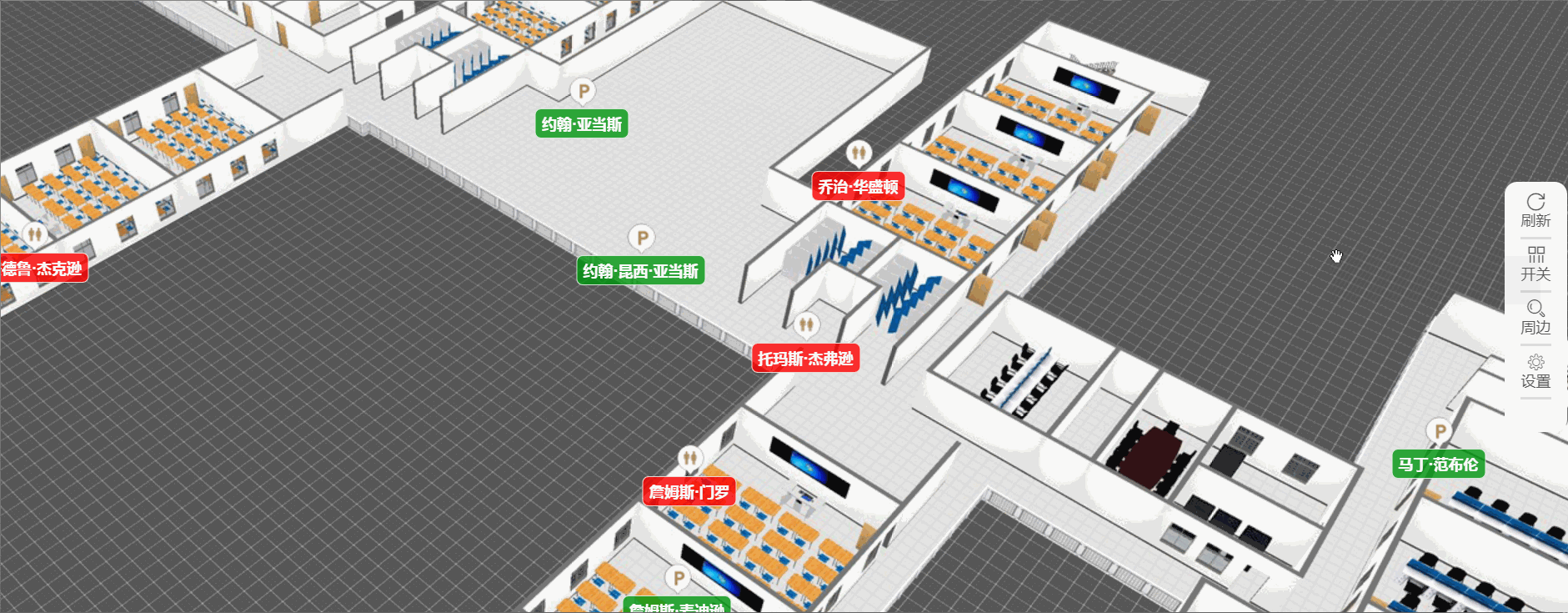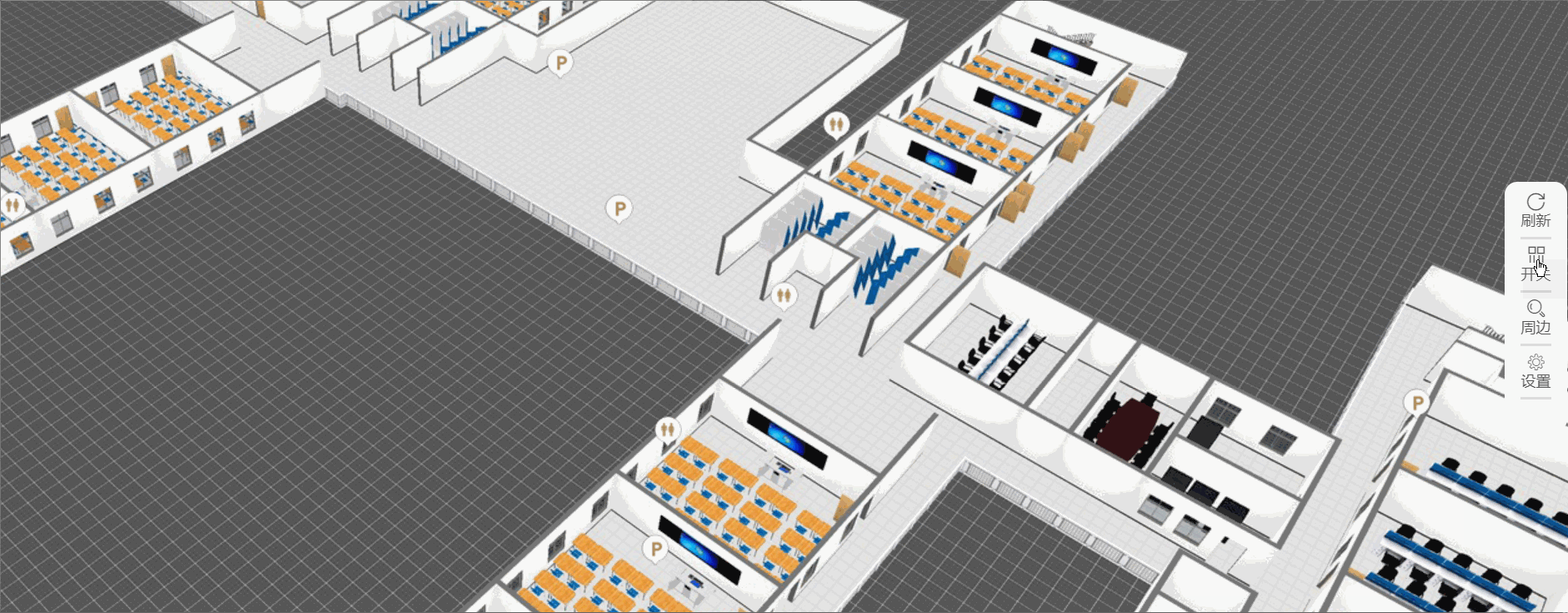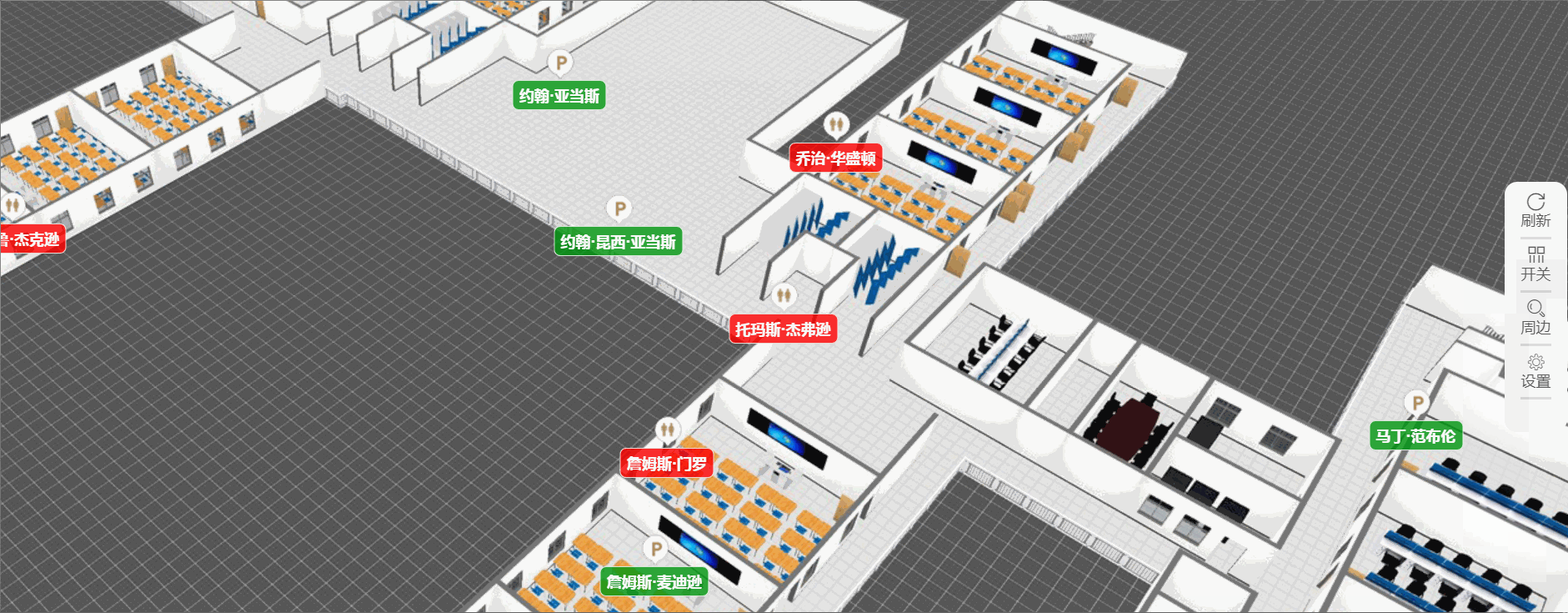
漏刻有时百度地图API实战开发(2)文本标签显示和隐藏的切换开关
项目说明 在百度地图开发的过程中,如果遇见大数据量POI标注展示或在最佳视野展示时,没有文本标签,会不清楚具体标注的代表的意义;如果同时显示大量的文本标签,又会导致界面杂乱且无法清晰查看,因此&#x…...

Flink往Starrocks写数据报错:too many filtered rows
Bug信息 Caused by: com.starrocks.data.load.stream.exception.StreamLoadFailException: {"TxnId": 2711690,"Label": "cd528707-8595-4a35-b2bc-39b21087d6ec","Status": "Fail","Message": "too many f…...
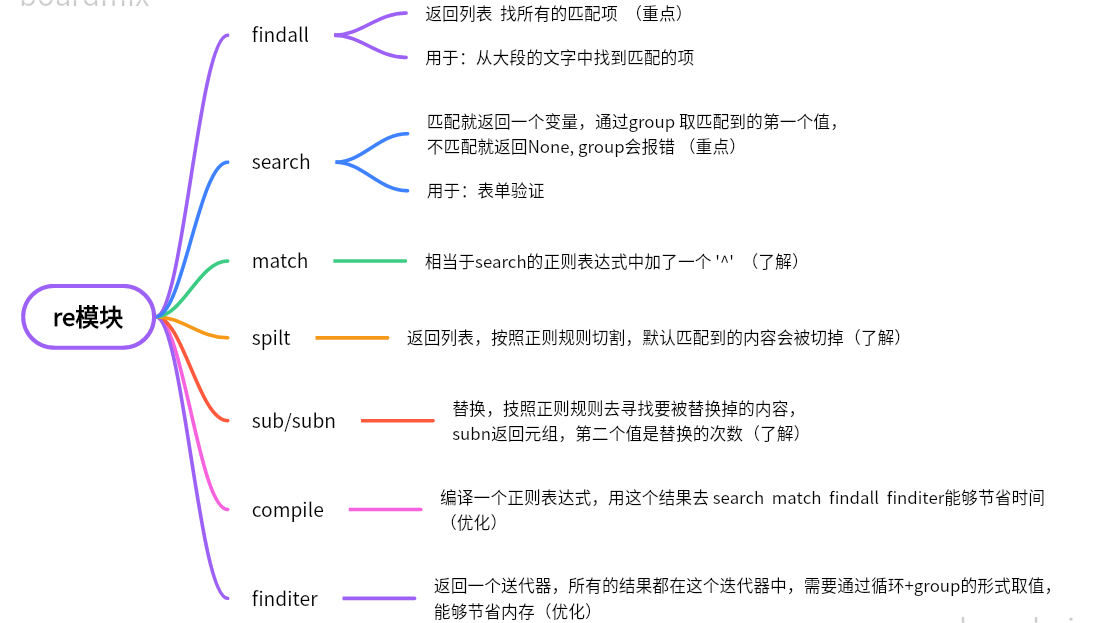
python-re模块
python之正则表达式-基础匹配https://blog.csdn.net/Python_1981/article/details/133777795python之正则表达式-元字符匹配https://blog.csdn.net/Python_1981/article/details/133778805 一、查找 1、findall 2、search 如果没有匹配到,会返回None, 使用group会报…...

SSM之spring注解式缓存redis
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《Spring与Mybatis集成整合》《Vue.js使用》 ⛺️ 越努力 ,越幸运。 1.Redis与SSM的整合 1.1.添加Redis依赖 在Maven中添加Redis的依赖 <redis.version>2.9.0</redis.…...

jmeter压测问题分析
1、 目录 1、jmeter压测java.net.BindException: Address already in use: connect问题处理: 2、jmeter压测:java.net.SocketException: Socket closed: : 之前未勾选same user on each iteration中报问题java.net.BindExcept…...

threejs CSS3DRenderer添加标签并设置朝向摄像机
一.由于CSS3DRenderer 是附加组件,必须显式导入 import { CSS3DRenderer, CSS3DObject } from three/examples/jsm/renderers/CSS3DRenderer.js;二.CSS3DRenderer特点 CSS3D不面向摄像机,会跟随场景缩放,不被模型遮挡,通过DOM事…...
基于若依的ruoyi-nbcio流程管理系统仿钉钉流程json转bpmn的flowable的xml格式(简单支持发起人与审批人的流程)续
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 之前生产的xml,在bpmn设计里编辑有些内容不正确,包括审批人,关联表单等…...
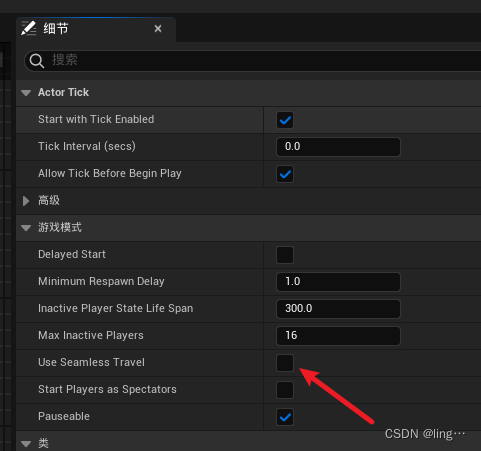
虚幻引擎:如何进行关卡切换?
一丶非无缝切换 在切换的时候会先断开连接,等创建好后才会链接,造成体验差 蓝图中用到的节点是 Execute Console Command 二丶无缝切换 链接的时候不会断开连接,中间不会出现卡顿,携带数据转换地图 1.需要在gamemode里面开启无缝漫游,开启之后使用上面的切换方式就可以做到无缝…...

工具类xxxUtil从application.properties中读取参数
一.原因 编写一个服务类的工具类,想做成一个灵活的配置,各种唯一code想从配置文件中读取,便有了这个坑。 二.使用value获取值为null, 这是因为这个工具类没有交给spring boot 来管理,导致每次都是new 一个新的,所以每…...
三国志14信息查询小程序(历史武将信息一览)制作更新过程05-后台接口的编写及调用
1,创建ASP.NET Web API项目 生成完毕,项目结构如下: 运行看一下: 2,后台接口编写 (1)在Models文件夹中新建一个sandata.cs文件(就是上篇中武将信息表的model文件) u…...

时序预测 | MATLAB实现基于SVM-Adaboost支持向量机结合AdaBoost时间序列预测
时序预测 | MATLAB实现基于SVM-Adaboost支持向量机结合AdaBoost时间序列预测 目录 时序预测 | MATLAB实现基于SVM-Adaboost支持向量机结合AdaBoost时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.Matlab实现SVM-Adaboost时间序列预测(风…...

useEffect和useLayoutEffect的区别
烤冷面加辣条的抖音 - 抖音 (douyin.com) 一、看下面的代码,即使调换useLayoutEffect和useEffect的位置依旧是useLayoutEffect先输出。 import { useState, useEffect, useLayoutEffect } from "react"; const Index () > {useLayoutEffect(() >…...

[科研图像处理]用matlab平替image-j,有点麻烦,但很灵活!
做材料与生物相关方向的同学应该对image-j并不陌生,前几天有个师兄拜托我用image-j分析一些图片,但使用过后发现我由于不了解image-j的工作流程而对结果并不确信,而且image-j的功能无法拓展,对有些图片的处理效果并不好࿰…...
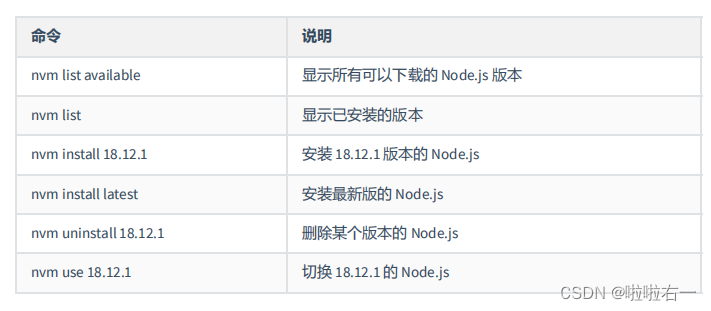
Node.js |(五)包管理工具 | 尚硅谷2023版Node.js零基础视频教程
学习视频:尚硅谷2023版Node.js零基础视频教程,nodejs新手到高手 文章目录 📚概念介绍📚npm🐇安装npm🐇基本使用🐇生产依赖与开发依赖🐇npm全局安装🐇npm安装指定包和删除…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
