AtCoder292 E 思维
题意:
给定一副n(n≤3000)n(n\leq 3000)n(n≤3000)个顶点,mmm条有向边的图,可以在图中添加有向边,求添加的最少边数,使得这副图满足:如果顶点aaa到顶点bbb有边,顶点bbb到ccc右有边,那么顶点aaa到顶点ccc也有边
Solution:
考虑一条单向链,按指向的方向按顺序是A,B,C,D,...A,B,C,D,...A,B,C,D,...
显然,A→B,B→CA\rightarrow B,B\rightarrow CA→B,B→C需要添加一条边A→CA\rightarrow CA→C,此时A→C,C→DA\rightarrow C,C\rightarrow DA→C,C→D需要添加A→DA\rightarrow DA→D。更一般的情况是,在从AAA出发能到达的顶点里,只有与AAA距离为1的不需要添加边,只需要和其他点建边即可,并查集不适合有向图,O(n)O(n)O(n)的搜索可以满足要求,每个顶点搜索一次,总复杂度O(n2)O(n^2)O(n2)
#include<iostream>
#include<vector>
#include<cstdlib>
#include<numeric>
#include<unistd.h>
#include<queue>
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<set>
#include<map>
#include<stack>
#include<utility>
#include<cctype>
#include<cassert>
#include<thread>
#include<bitset>
using namespace std;using ll=long long;
const int N=2e5+5,inf=0x3fffffff;
const long long INF=0x3fffffffffffffff,mod=998244353;struct way {int to,next;
}edge[N<<1];
int cnt,head[N];void add(int u,int v) {edge[++cnt].to=v;edge[cnt].next=head[u];head[u]=cnt;
}int n,m,dis[N],vis[N];int main() {#ifdef stdjudgefreopen("in.txt","r",stdin);auto TimeFlagFirst=clock();#endifstd::ios::sync_with_stdio(false);std::cin.tie(nullptr);cin>>n>>m;for(int i=1;i<=m;i++) {int u,v;cin>>u>>v;add(u,v);}int tot=0;queue<int>q;for(int i=1;i<=n;i++) {for(int j=1;j<=n;j++) vis[j]=false;while(!q.empty()) q.pop();q.push(i);while(!q.empty()) {int u=q.front(); q.pop();vis[u]=true;for(int j=head[u];j;j=edge[j].next) {int v=edge[j].to;if(vis[v]) continue;q.push(v);}}for(int j=1;j<=n;j++) {if(i!=j&&vis[j]) tot++;}for(int j=head[i];j;j=edge[j].next) tot--;}cout<<tot<<endl;#ifdef stdjudgefreopen("CON","r",stdin);std::cout<<std::endl<<"耗时:"<<std::clock()-TimeFlagFirst<<"ms"<<std::endl;std::cout<<std::flush;system("pause");#endifreturn 0;
}
相关文章:

AtCoder292 E 思维
题意: 给定一副n(n≤3000)n(n\leq 3000)n(n≤3000)个顶点,mmm条有向边的图,可以在图中添加有向边,求添加的最少边数,使得这副图满足:如果顶点aaa到顶点bbb有边,顶点bbb到ccc右有边,…...

20230309英语学习
What Is Sleep Talking? We Look at the Science 为什么人睡觉会说梦话?来看看科学咋说 Nearly everyone has a story about people talking in their sleep.Though it tends to be more common in children, it can happen at any age:A 2010 study in the jour…...
CAD转换PDF格式怎么弄?教你几种方法轻松搞定!
CAD是从事与艺术创作相关等行业的打工人们必需的工作软件,可以用来完成建筑设计图、设计图纸等。在日常的工作中,一些伙伴经常需要传输图纸给合作方来完成探讨。但是CAD图纸需要使用专业软件才能打开,这就给文件传送带来了一定的困难。而且传…...

AtCoder 259E LCM
题意: 以唯一分解形式给出nnn个数: aipi,1ei,1pi,2ei,2...pi,tei,ta_{i}p_{i,1}^{e_{i,1}}p_{i,2}^{e_{i,2}}...p_{i,t}^{e_{i,t}} aipi,1ei,1pi,2ei,2...pi,tei,t 现在可以将某个数改为111,求所有改法中,有多少个…...

MQTT协议-取消订阅和取消订阅确认
MQTT协议-取消订阅和取消订阅确认 客户端向服务器取消订阅 取消订阅的前提是客户端已经通过CONNECT报文连接上服务器,并且订阅了一个主题 UNSUBSCRIBE—取消订阅 取消订阅的报文同样是由固定报头可变报头有效载荷组成 固定报头由两个字节组成,第一个…...
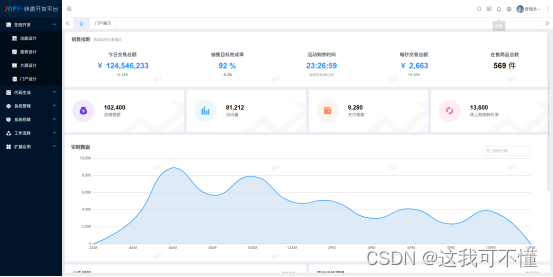
90后小伙,用低代码“整顿”旅游业,年入2000万,他是怎么做到的?
热爱旅游的92年成都小伙猴哥,大学毕业后开了一家旅行社,主要从事川藏、云南定制游服务。 从今年春节开始,国内各地旅游业开始复苏,向旅行社打电话咨询的人越来越多。 旅游的人多是好事,也是一种烦恼,因为…...

C51---PWM 脉冲宽度调制
1.PWM:脉冲宽度调制,它是通过一系列脉冲宽度进行调制,等效出所需要的波形(包含形状以及幅值)。对模拟信号电平进行数字编码。也就是说通过调节占空比的变化来调节信号、能量等的变化,占空比就是指在一个周期内,信号处于…...

毕业设计 基于51单片机WIFI智能家居系统设计
基于51单片机WIFI智能家居系统设计1、毕业设计选题原则说明(重点)2、项目资料2.1 系统框架2.2 系统功能3、部分电路设计3.1 STC89C52单片机最小系统电路设计3.2 ESP8266 WIFI电路设计3.3 DHT11温湿度传感器电路设计4、部分代码展示4.1 LCD12864显示字符串…...
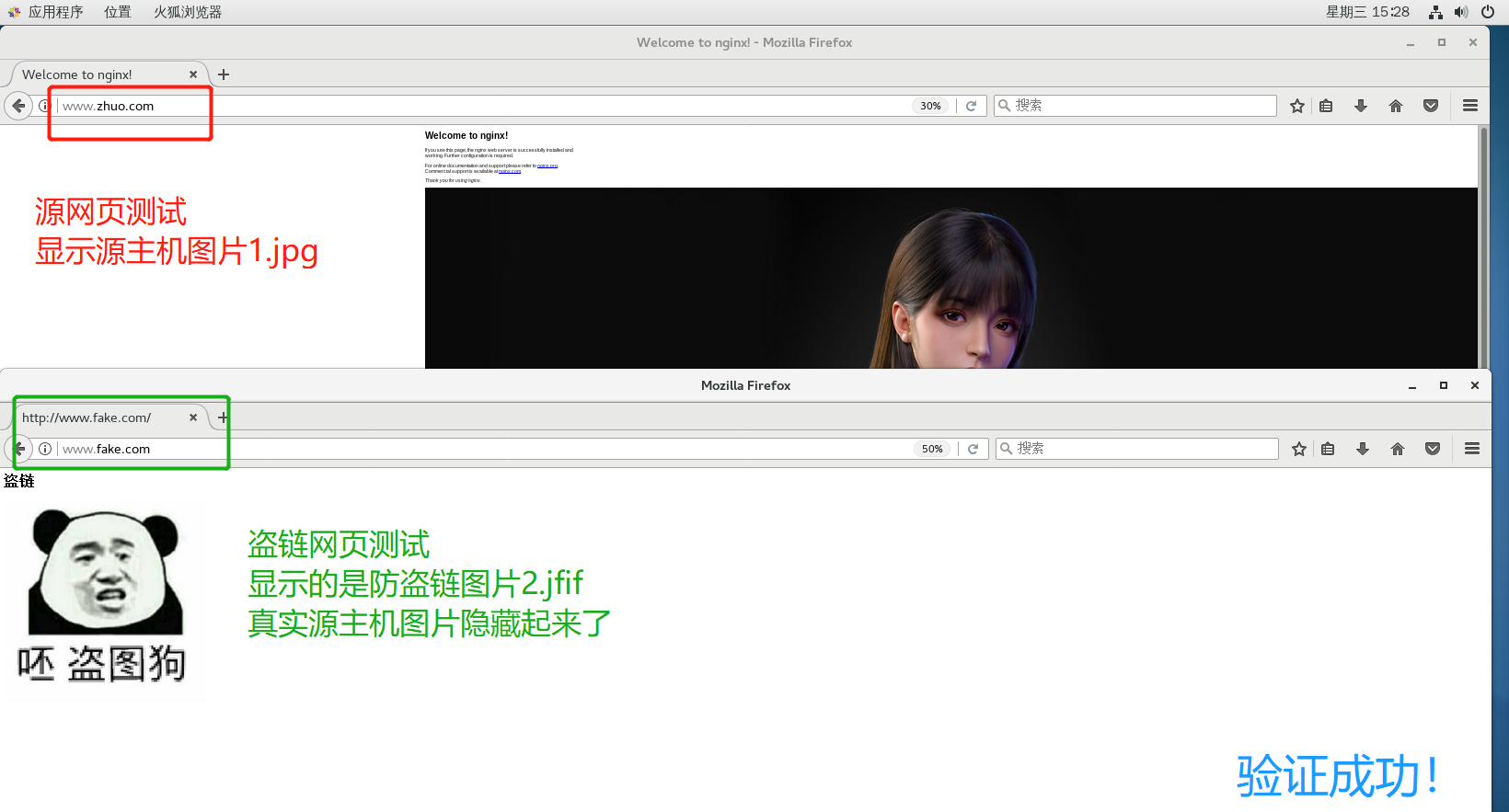
Nginx服务优化措施与配置防盗链
目录 一.优化Nginx的相关措施 二.隐藏/查看版本号 三.修改用户与组 四.设置缓存时间 五.日志切割脚本 六.设置连接超时控制连接访问时间 七.开启多进程 八.配置网页压缩 九.配置防盗链 1.配置web源主机(192.168.79.210 www.zhuo.com) 1.1 安装…...

Java 某厂面试题真题合集
哈喽~大家好,这篇来看看Java 某厂面试题真题合集。 🥇个人主页:个人主页 🥈 系列专栏:【日常学习上的分享】 🥉与这篇相关的文章: Spr…...

很特别的5G市场,5.75亿部手机,却有11亿5G用户,这是怎么了?
中国在5G商用方面已取得了巨大的成绩,这是毋庸置疑的,不过近期公布的一份数据却相当特别,5G手机用户数为5.75亿,而开通了5G套餐的用户数却已超过11亿,这数据对比有点意思。中国在5G商用方面推进很快,建成的…...

go modules
文章目录1. 简介示例1. 示例——同一项目2. 示例——不同项目3. 示例——添加远程模块依赖库1. 简介 go module是Go1.11版本之后官方推出的版本管理工具,并且从Go1.13版本开始,go module将是Go语言默认的依赖管理工具。到今天Go1.14版本推出之后Go modu…...
Baklib客户故事:快递助手ERP
快递助手ERP以多平台多店铺订单管理为核心,集打单发货、商品、库存、采购、售后于一体,中小商家易上手的轻量级ERP,可以满足满足微商、自建商城、档口货源网、一件代发等不同类型客户的打单需求,通过开放平台API接口,自…...
MongoDB学习(java版)
MongoDB概述 结构化数据库 结构化数据库是一种使用结构化查询语言(SQL)进行管理和操作的数据库,它们的数据存储方式是基于表格和列的。结构化数据库要求数据预先定义数据模式和结构,然后才能存储和查询数据。结构化数据库通常…...

RK3568平台开发系列讲解(显示篇)什么是DRM
🚀返回专栏总目录 文章目录 一、DRM介绍二、DRM与framebuffer的区别沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇文章将介绍什么是DRM。 一、DRM介绍 DRM 是 Linux 目前主流的图形显示框架,相比FB架构,DRM更能适应当前日益更新的显示硬件。 比如FB原生不支…...

Python蓝桥杯训练:基本数据结构 [二叉树] 上
Python蓝桥杯训练:基本数据结构 [二叉树] 上 文章目录Python蓝桥杯训练:基本数据结构 [二叉树] 上一、前言二、有关二叉树理论基础1、二叉树的基本定义2、二叉树的常见类型3、二叉树的遍历方式三、有关二叉树的层序遍历的题目1、[二叉树的层序遍历](http…...
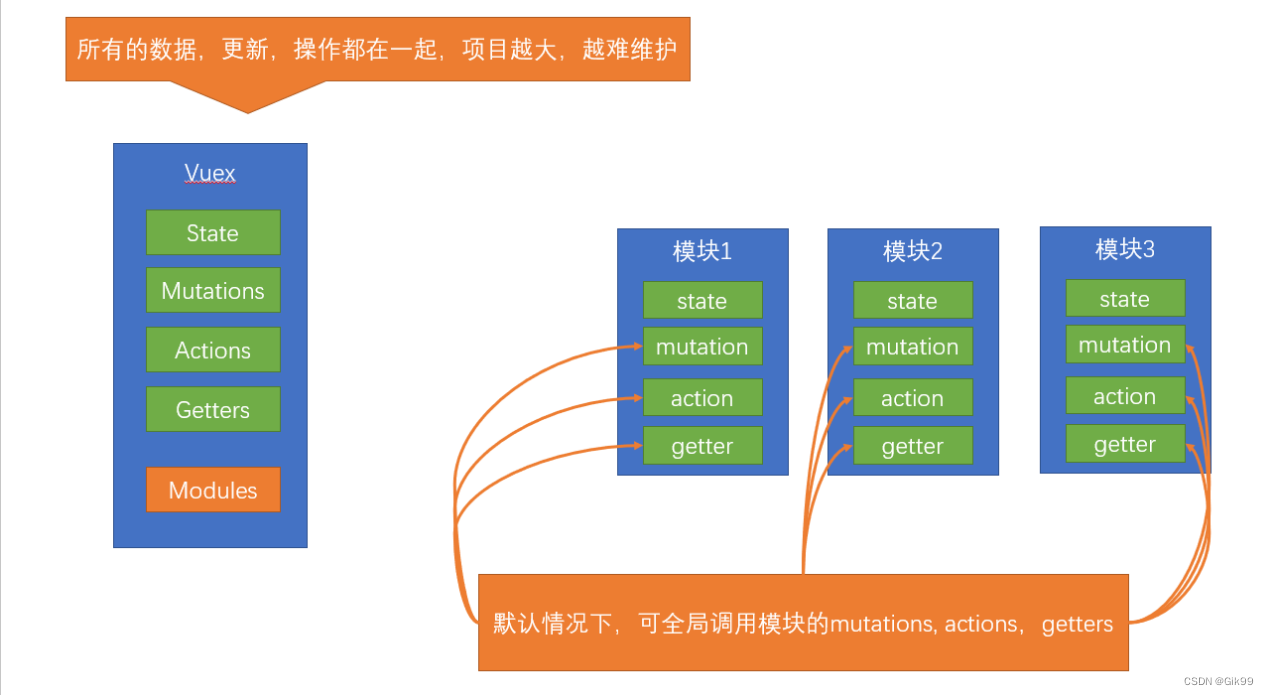
vuex基础之初始化功能、state、mutations、getters、模块化module的使用
vuex基础之初始化功能、state、mutations、getters、模块化module的使用一、Vuex的介绍二、初始化功能三、state3.1 定义state3.2 获取state3.2.1 原始形式获取3.2.2 辅助函数获取(mapState)四、mutations4.1 定义mutations4.2 调用mutations4.2.1 原始形式调用($store)4.2.2 辅…...

WebSphere中间件漏洞总结
WebSphere中间件漏洞总结 一、WebSphere简介 WebSphere为SOA(面向服务架构)环境提供软件,以实现动态的、互联的业务流程,为所有业务情形提供高度有效的应用程序基础架构。WebSphere是IBM的应用程序和集成软件平台,包含所有必要的中间件基础架构(包括服务器、服务和工具)…...

Unity之ASE实现影魔灵魂收集特效
前言 我们今天来实现一下Dota中的影魔死亡后,灵魂收集的特效。效果如下: 实现原理 1.先添加一张FlowMap图,这张图的UV是根据默认UV图,用PS按照我们希望的扭曲方向修改的如下图所示: 2.通过FlowMap图,我…...

半入耳式耳机运动会不会掉、佩戴超稳固的运动耳机推荐
现在越来越多的人开始意识到运动的重要性,用运动给身体增加一道“防护墙”是最好的生活方式了,不过,日复一日做着几乎相同的动作,难免索然无味,所以很多人都会选择在运动时戴上耳机听歌解闷,这时候也有不少…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
